考虑边界条件不确定性的地下水污染风险分析

李久辉,卢文喜*,辛 欣,罗建男, 常振波 (1.吉林大学地下水资源与环境教育部重点实验室,吉林长春 130021；2.吉林大学环境与资源学院,吉林 长春 130021)

早期研究中,确定性污染质运移数值模拟模型通常用来预测地下水污染质运移情况,确定性模拟模型未考虑输入模拟模型参数和边界条件的不确定性,输入模型参数及边界条件均为定值,其输出结果与输入对应且确定唯一,依靠其确定结果难以评估模拟模型输出结果的可靠程度,致使决策者面临决策失败的风险[1].故将输入模型参数和边界条件的不确定性引入研究,对于预测地下水污染质运移有重要意义[2].

地下水污染风险分析研究层见叠出,但诸多研究将数学模型处理为确定性模型,忽略了输入数值模拟模型参数、边界条件的不确定性.尤其,对于考虑边界条件不确定性的研究更是寥寥无几.近些年来,不确定性分析的发展可谓方兴未艾.吴吉春等[3]分析了地下水模型不确定性的来源和分类,并且,对不确定性的来源和模型输出的不确定性进行了讨论,提出了地下水模拟不确定性分析的发展前景. Guillaume等[4]将地下水经济管理与地下水模拟模型结合,运用动态耦合经济-地下水模型对地下水开采规律进行不确定性分析.Arnold等[5]将模型参数不确定性考虑到核素运移模拟中,对核素运移及吸附时间进行预报.欧阳琦等[6],常振波等[7]考虑污染质运移数值模拟模型中水文地质参数的不确定性,通过分析其不确定性对污染质运移的影响,对研究区遭受污染风险进行分析与预报.Hauser等[8]将潜水含水层地质结构和水文地质参数的不确定性因素考虑到数值模拟模型中,发现两者共同作用导致了地下水位的不确定性.多数研究均将模型参数不确定性做为研究核心,忽略了边界条件不确定性的影响.

然而在地下水运移数值模拟的过程中,模拟预报结果的正确与否和边界条件处理得是否恰当密切相关.在人类活动影响强度日益增大的今天,处理边界条件时,往往会面临一些复杂的问题.原因在于边界处的水流状况,不仅受到自然因素的影响,而且还受到人类活动的影响,由于这种耦合效应影响,在模拟预测阶段,边界条件具有很大不确定性.所以在建立研究区的数学模拟模型之前,根据研究区水资源开采计划、补径排关系等相关资料,对边界条件做出合理预报,辅助研究者进行更符合实际的地下水污染质运移预测.

针对于地下水溶质运移的不确定性分析,前人多研究参数的不确定性对模拟模型影响,对于边界条件的不确定并未多加考虑,本文主要研究第一类边界条件—已知水头边界不确定性对污染质运移结果影响.在对已知水头边界预报后,将其不确定性与地下水污染质运移预测相结合,运用Monte Carlo方法针对具体算例进行阐明与分析.首先将模拟预报得到的已知水头边界(第一类边界),做为输入模拟模型的随机变量,其它参数作为定值,建立模拟模型的替代模型完成Monte Carlo过程,最后将污染风险评估与不确定性分析结果相结合,完成污染风险预警与分析.运用模拟模型的替代模型完成Monte Carlo模拟过程,不但可以克服反复调用模拟模型产生大量计算负荷的弊端,而且能够以较高的精度刻画模拟模型的输出结果.在大量节约计算成本的同时减少研究耗时.

1 研究方法

1.1 研究区概况

本文用一假想例子对此问题进行研究.建立一个东西长 800m,南北宽 600m,含水层厚度为35m 的不规则研究区域,含水层为均质各向同性潜水非稳定流,含水层岩性I区主要为粗砂,II区为粗砂夹中砂.初始水位为26m,水流方向由西北流向东南,在垂向上接受大气降水补给,多年平均降水量为 616mm,忽略蒸发腾散消耗量.区域内地表平坦,西北侧边界 Г2有一河流,切穿潜水含水层且与其具有较好的水力联系.东南侧边界 Г4有一湖泊,切穿潜水含水层且与其具有较好的水力联系.西北侧边界Г2及东南侧边界Г4均可视为给定水头边界,与含水层有较好的水力联系.东北侧边界 Г1,及西南侧边界 Г3均为微透水介质,可视为隔水边界.研究区可以划分为两个参数分区,其相关参数取值见表1:

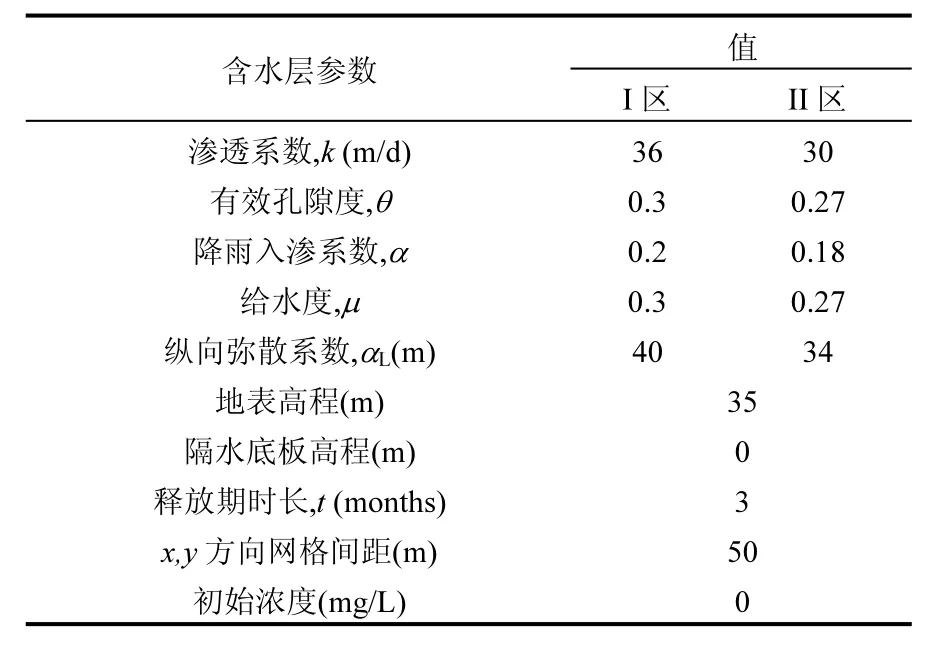
表1 水文地质参数取值Table 1 hydrogeological parameters

研究区内有3口观测井,编号分别为井1,2,3.区内有一化工厂,因污水池防渗工作出现疏漏,致使污水泄漏到潜水含水层.为预测污染泄露对研究区的影响,建立污染质运移数值模拟模型模拟预测污染质运移,模拟年限为1.5年,每3个月为一个时段,共计 6个模拟时段.污水泄露发生在前 3个释放时段,污染物释放强度为1500mg/L,污水泄漏量为 600m3/d.将污染物视为不会发生化学变化及生物转化与迁移的氯化物.潜水含水层污染物的初始浓度为零,给定水头边界 Г2,Г4,隔水边界 Г1,Г3分别视为零浓度边界和零通量边界.研究区污染源观测井布设位置见图1.

研究区已知水头边界 Г4受人工开采影响比较严重,湖泊东南侧开采地下水量逐年增长,导致湖泊水位逐年下降.汛期与平枯水期降雨量对湖泊水位也有影响,考虑人工开采影响及降雨径流影响是十分必要的.所以在预测污染质运移之前,需要对边界水头进行预报.

图1 污染源、观测井布设位置Fig.1 location of pollution source and observation well

1.2 边界条件的预报

研究区东南侧已知水头边界 Г4的东南部约300m 的区域内,建有 5口开采井,开采井的开采量逐年增大(各时段开采量波动范围见图2),对研究区东南侧边界的水头值影响明显.观测井各时段的开采量见图 2,研究区各时段降雨量见图 3.根据源汇项特征和研究区水文地质条件,运用数值法预报各时段边界水头值.各时段预报的边界水头值见表2.

图2 各时段人工开采量(m3/d)Fig.2 artificial exploitation in different periods (m3/d)

图3 各时段降雨量(mm)Fig.3 rainfall in different periods (mm)

各时段边界的水头值在一定范围内波动,水头值在人工开采及自然条件的耦合作用下,呈现出降低的趋势.

表2 各时段水头取值范围Table 2 fluctuation of head value at different periods

下面研究边界条件-水头值的大小对于研究区污染质运移的影响.

1.3 污染质运移数值模拟模型的建立

为了对研究区地下水污染质运移进行研究,需要建立地下水污染质运移数值模拟模型,对污染质的运移进行模拟.根据研究区的初始条件与边界条件,建立地下水水流数值模拟模型:

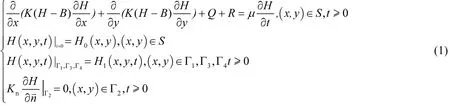
式中:K是含水层渗透系数, m/d;H是潜水水位,m;B是潜水含水层底板高程, m;Q是人工开采强度, m/d;R是降水入渗补给量, m/d;µ是含水层给水度,无量纲;S是模拟区范围;Г2是定水头边界;Г1,Г3,Г4是零流量边界;Kn是边界法向量上的渗透系数, m.污染质随水流运移,在建立好水流数值模型基础之上,建立地下水污染质运移数值模拟模型:

式(2)中:S是模拟区范围;Г2是定浓度边界;Г1,Г3,Г4是零弥散通量边界;n是含水层介质的孔隙度,无量纲;c是污染质浓度,单位 mg/L;Dx,Dy是水动力弥散系数在 x、y方向的分量,单位m2/d;vx,vy为渗透流速v在x、y方向上的分量,单位 m/d. I为单位时间单位液相体积内溶质质量的增减量,mg/(d.m3).

建立的地下水污染质运移模拟模型运用GMS软件中的Modelflow与MT3D工具箱进行模拟计算.

1.4 替代模型的建立

替代模型是模拟模型输入输出响应关系的代替,它不但可以大幅度减少多次调用模拟模型产生的计算负荷,且能够以较高的精度刻画出模拟模型输入输出数据.本研究中的输入即是通过边界条件预报得到的各时段的水头的取值,输出则是模型在水头不同取值情况下运行各时段各观测井氯化物的浓度值.

本文运用 Kriging方法建立替代模型.Kriging方法是一种基于最小估计方差的无偏估计法,是由南非地质学家Krige[9]提出的一种应用于地质领域的预测方法.目前 Kriging方法广泛的应用于建立替代模型,运用其原理建立的替代模型不但功能上逼近模拟模型,且调用过程相对简单,大幅度减少了解决复杂问题的工作量,节省了大量计算成本[10],本文参照替代模型构建的原理与步骤[11-15],运用 MATLAB软件编写并调试程序,完成替代模型构建.

首先利用拉丁超立方抽样方法(LHS)在随机变量(水头值)的取值范围内(表 2)对各时段的水头值进行抽样,共抽样两大组,第一大组抽样 45组,第二大组抽样 10组.将两大组参数作为输入值,分别输入到污染质运移数值模拟模型中,获得两大组中各个输入参数样本对应的输出值,两大组的输入与输出值分别构成训练样本,检验样本.运用 Kriging方法应用第一大组的训练样本建立替代模型.然后应用第二大组的 10 组检验样本对建立的替代模型的精度进行检验.替代模型精度检验情况见图 4.由图 4可知,替代模型运算结果与模拟模型输出结果,相对误差均未超过0.01,精度很高,可以代替模拟模型求解.

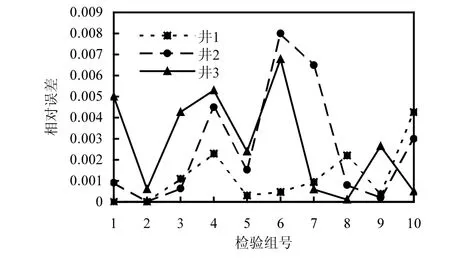
图4 拟合精度检验Fig.4 Fitting accuracy test

1.5 Monte Carlo模拟

Monte Carlo方法是一种概率统计方法, Monte Carlo模拟通常要进行成百上千次的试验,在模拟过程中认为随机变量的概率分布函数已知,通过随机抽样方法得到多组输入变量,然后将随机变量输入到模型中得到大量的输出, 每组输入输出看做是一次统计试验,通过对输出(如地下水中氯化物浓度)的统计可以得到均值,方差等统计估计量,并得到其输出结果的概率分布情况.

本次研究利用拉丁超立方抽样法(LHS)对各时段水头值分别抽样600组,作为参数样本,输入到建立好的替代模型,得到600组响应输出(即污染物浓度值),然后对这600组响应输出进行不确定性分析.分别对观测井1,2,3各时段的污染物浓度值及其遭受污染风险进行统计与分析.

文中运用Monte Carlo方法进行了600次模拟试验.若 600次试验都需要调用模拟模型, 每次调用模拟模型计算耗时约 2min,总耗时约1200min.将模拟模型的600次输入一次输入到训练好的替代模型中,替代模型可以在1min内输出600次输入对应的输出,这样节约了大量人力和时间,减少了不必要计算负荷的产生,又保持了一定的拟合精度.

文中运用的是假想例子,替代模型的优点不是十分明显,在实际例子中模拟模型运行一次可能需要 1h,甚至更多时间,成百上千次的调用模拟模型,产生的计算负荷之大,耗费的时间之长是难以想象的,这时运用替代模型就可以解决上述问题.

2 结果与讨论

本文主要对第 6时段末刻的污染物浓度进行统计分析(实际上各个时段的观测井污染物风险分析及污染物浓度估计均可以计算,并作为统计分析对象).运用替代模型输出3口观测井第6时段末刻的 600组污染物浓度值.利用此数据对观测井的污染物浓度进行估计,并对观测井遭受污染风险进行统计与分析.

在统计分析之前,首先讨论边界条件的不确定性对污染物浓度运移的影响.

2.1 对比分析

运用600组污染物浓度数据计算出第6时段末刻污染物浓度最小值与最大值,与边界条件取定值(数值模拟模型中各个时段中水头值保持不变)计算得到的污染物浓度进行对比,见表3,对比发现三种情形下 3口观测井的污染物浓度值相差很大,说明边界条件的不确定性对污染质运移有较大影响.

在不考虑边界水头不确定性的情况下,第 6时段末刻井3中污染物浓度很小,几乎未被污染.在考虑边界条件不确定性的情况下,观测井1、2、3中污染物浓度明显增大,造成这种结果的原因是人工开采及自然因素的耦合作用使地下水水力梯度变大,地下水流速增大,在相同的时间段内更多的污染质运移到观测井中,导致观测井中污染物浓度增大.可见考虑边界条件不确定性具有重要的实际意义.

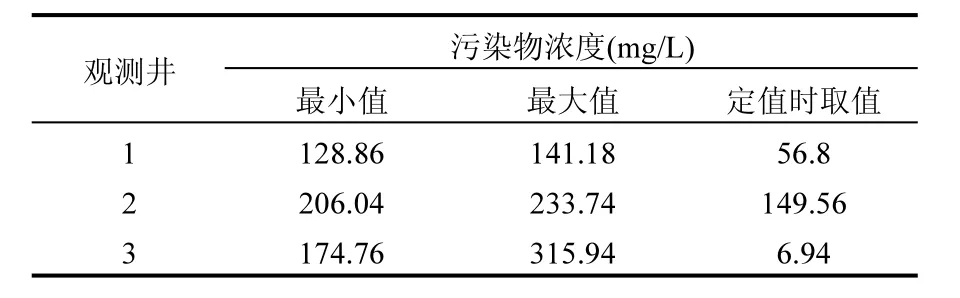
表3 污染物浓度对比Table 3 Comparison of pollutant concentration

除了对观测井内的污染物浓度进行对比,也对研究区第 6时段末刻的污染质运移情况进行对比.图 5(a)是没有对边界条件进行预报,将边界条件作为定值输入模型,得到的污染晕分布图.图5(b)是对边界条件进行预报,将各时段边界条件水头值作为随机变量输入模型,得到的污染晕分布图.由图5可知,预测边界条件,并考虑边界条件的不确定性对污染质运移情况影响很大,在第 6时段末刻时,两种情况下的污染晕覆盖情况有很大差距.(b)图中,因为水力梯度的增大,污染质运移速度更快,污染晕分布范围更大.

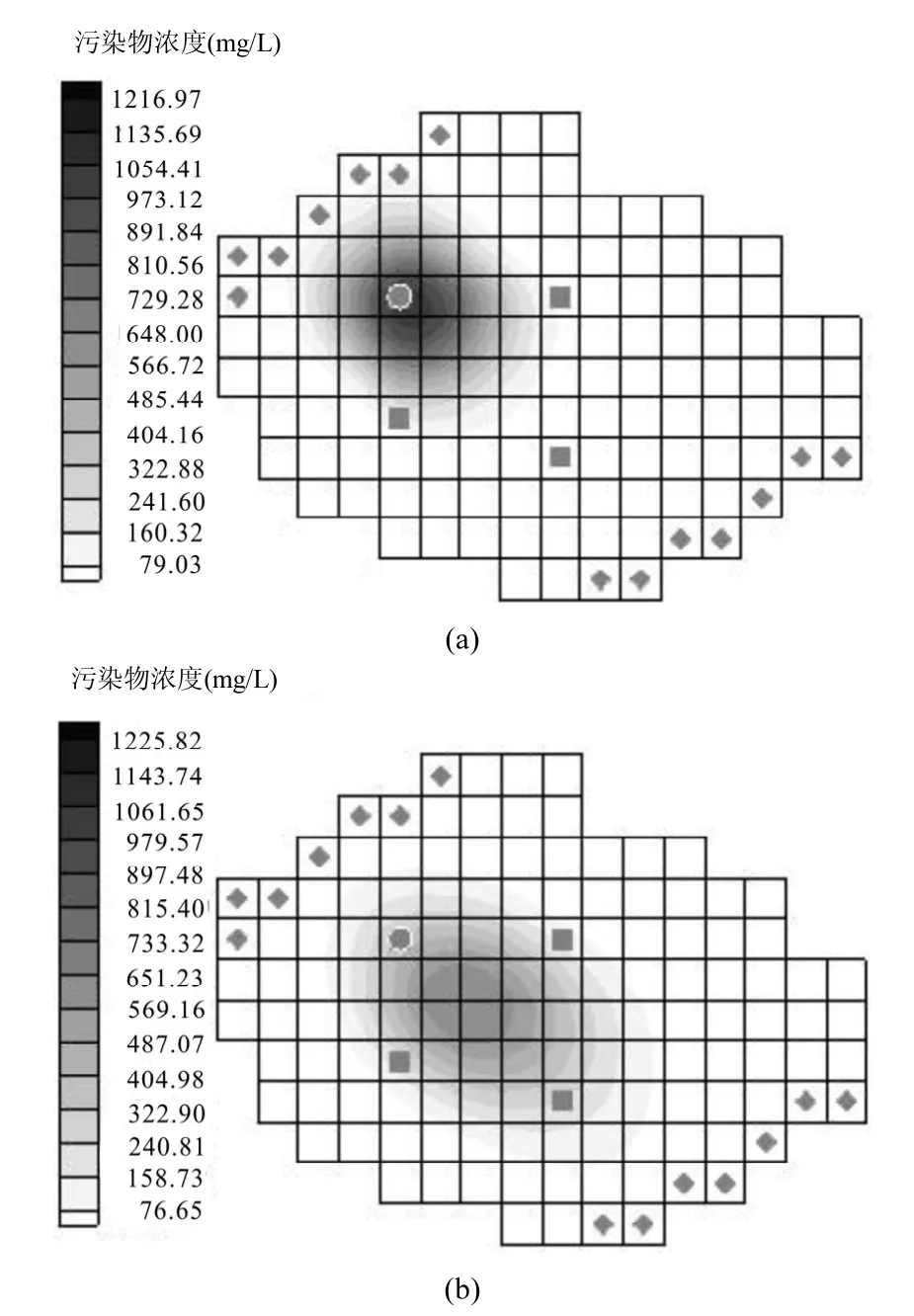
图5 第6时段末刻污染晕分布情况Fig.5 Distribution of pollution halo at the end of sixth periods

2.2 污染物浓度统计指标分析

运用 600组污染物浓度数据集进行分析,绘制污染物浓度分布直方图,并对各观测井污染物浓度值做出统计.结合表3和图6～8可知,在第6个时段末刻,井2遭受污染程度最严重,井1次之,井3遭受污染程度最小,原因是井2与污染源距离较小,最先受到污染,所以遭受污染最严重.井3污染物浓度波动最大,可能因为井 3距离边界条件距离较近,受边界条件影响明显.3口观测井的污染物浓度均值分别为 412.3mg/L、621mg/L、97mg/L.

图6 井1污染物浓度频数Fig.6 histogram of pollutant concentration frequency for four monitoring periods of well 1

图7 井2污染物浓度频数Fig.7 histogram of pollutant concentration frequency for four monitoring periods of well 2

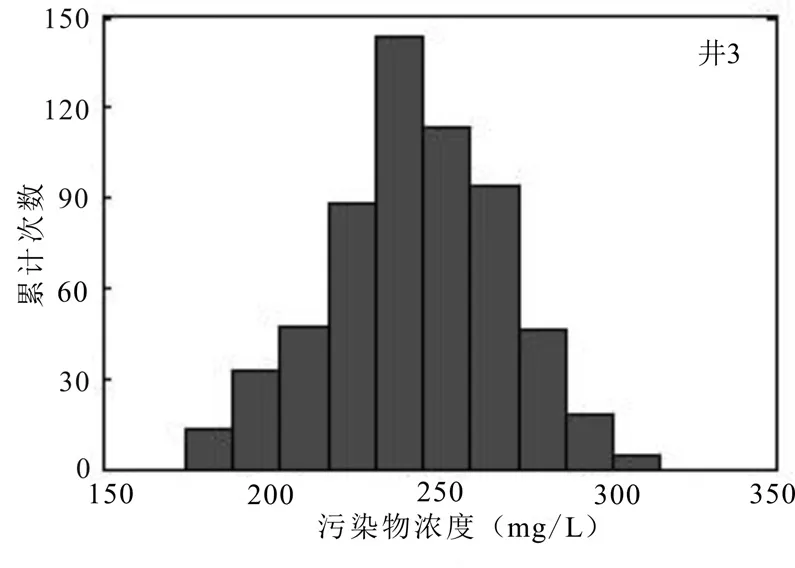
图8 井3污染物浓度频数Fig.8 histogram of pollutant concentration frequency for four monitoring periods of well 3

表4 各观测井污染物输出值统计指标(mg/L)Table 4 Output statistic indexes of observation wells(mg/L)

2.3 污染物浓度区间估计

相比于确定的输出,一定置信水平下的污染物取值区间,往往更有借鉴意义,文中运用切比雪夫[16]不等式,对一定置信水平下的观测井污染物浓度区间进行估计.

式(3)中:P是置信水平;E(X)是各个时段的观测井污染物浓度值均值; D(X)是各个时段的观测井污染物浓度值方差; ε是任意给定正数.利用上式对3口观测井不同置信水平下的的污染物浓度区间进行估计,见表5.

上表给出了 5口观测井不同置信水平下的污染物浓度范围,由表分析知置信水平越低,污染物浓度区间范围越小;置信水平越高,污染物浓度区间范围越大.决策者可以规划需要,选择相信不同置信水平下的污染物浓度范围.

表5 不同置信水平井浓度值的区间估计(mg/L)Table 5 interval estimates concentration values of wells with different confidence levels (mg/L)

2.4 污染物超标风险分析

运用输出数据,参照《地下水质量标准》[17],计算得到第6时段末刻地下水污染物(氯化物)浓度达到I、II、III类水标准的概率,见表6.可以为研究区地下水的合理利用提供参考据.

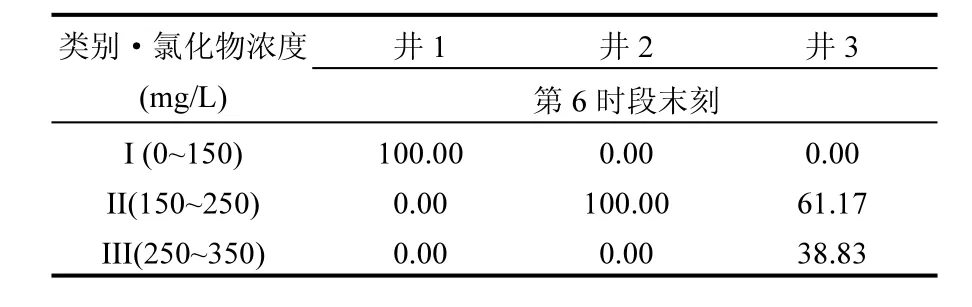
表6 观测井污染物超标风险分析(%)Table 6 risk statistics of single well pollutant exceeding standard (%)

3 结论

3.1 替代模型是数值模拟模型输入输出响应关系的代替,它不但可以大幅度减少多次调用数值模拟模型产生的计算负荷,且能够以较高的精度刻画出模拟模型输入输出数据,在大量节约计算成本的同时减少研究耗时.

3.2 边界条件(第一类边界条件)的不确定性是客观存在的,而且对于地下水中污染质运移有一定程度的影响.研究地下水污染质运移规律及运移情况时,第一类边界条件在一定范围内变化,将其不确定性考虑在内对于污染质运移规律研究是十分必要的.

3.3 通过对 Monte Carlo模拟结果进行统计与分析, 发现考虑与不考虑边界条件不确定性的研究区污染羽分布差异较大,I、II、III类水所对应的观测井污染物超标风险不同.应用切比雪夫不等式可以对不同置信水平下的污染物浓度范围进行估计.

[1]Zeng X K, Wang D, Wu J C. Sensitivity analysis of the probability distribution of groundwater level series based on information entropy [J]. Stoch Env. Res. Risk A, 2012,26:345-356

[2]顾文龙,卢文喜,马洪云,等.地下水值模拟分析中降水入渗补给强度及渗透系数不确定性评价 [J]. 水电能源科学, 2015,(11):45-48,64.

[3]Jichun W U, Zeng X K. Review of the uncertainty analysis of groundwater numerical simulation [J]. Chinese Science Bulletin,2013,58(25):3044-3052.

[4]Guillaume J H A, Qureshi M E, Jakeman A J. A structured analysis of uncertainty surrounding modeled impacts of groundwater-extraction rules [J]. Hydrogeology Journal, 2012,20(5):915-932.

[5]Arnold B W, Kuzio S P, Robinson B A. Radionuclide transport simulation and uncertainty analyses with the saturated-zone site-scale model at Yucca Mountain, Nevada. [M]// Supplement to the Journal of the Royal Statistical Society. Royal Statistical Society, 2003:1828-1843.

[6]欧阳琦,卢文喜,侯泽宇,等.基于替代模型的地下水溶质运移不确定性分析 [J]. 中国环境科学, 2016,36(4):1119-1124.

[7]常振波,卢文喜,辛欣,等.基于灵敏度分析和替代模型的地下水污染风险评价方法 [J]. 中国环境科学, 2017,37(1):167-173.

[8]Hauser J, Wellmann F, Trefry M. Water Table Uncertainties due to Uncertainties in Structure and Properties of an Unconfined Aquifer. [J]. Groundwater, 2018,56(2):251-255.

[9]Krige D G．A Statistical Approach to Some Mine Valuations and Allied Problems at the Wit—watersrandr [D]. Wilwatersrand:University of Wit-watersrand, 1951.

[10]Luo Jiannan, Lu Wenxi. Comparison of surrogate models with different methods in groundwater remediation pro⁃cess [J].Journal of Earth System Science, 2014,123(7):1579-1589.

[11]Toal D J J. Some considerations regarding the use of multi-fidelity Kriging in the construction of surrogate models [J].Structural & Multidisciplinary Optimization, 2014,51(6):1223-1245.

[12]Passos F, González-Echevarría R, Roca E, et al. Surrogate modeling and optimization of inductor performances using Kriging functions [C]// Conference: 2015 International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications To Circuit Design., 2015:1-4.

[13]Kwon H, Yi S, Choi S. Numerical investigation for erratic behavior of Kriging surrogate model [J]. Journal of Mechanical Science and Technology, 2014,28(9):3697-3707.

[14]Schmit L A, Farshi B. Some Approximation Concepts for Structural Synthesis [J]. Aiaa Journal, 2015,12(5):692-699.

[15]王晓锋,席 光,王尚锦.Kriging与响应面方法在气动优化设计中的应用 [J]. 工程热物理学报, 2005,26(3):423-425.

[16]Wei-Kai Lai. Rearrangement Inequality and Chebyshev′s Sum Inequality on Positive Tensor Products of Orlicz Sequence Space with Banach Lattice [J]. Journal of Systems Science and Mathematical Sciences, 2014,4(8):574-578.

[17]GB/T 14848-1993 地下水质量标准 [S].