基于神经网络的相空间重构短期风速发电功率在线预测

韩亚军

（重庆城市职业学院信息工程系，重庆 402160）

风电场短期风速的预测关系到风电并网科学与技术的稳定性、电网安全和分配调度等问题，是风电行业需要预测的重要指标。经研究，风速时间序列具有混沌特性，受温度、气压、地形、海拔、纬度等多因素影响，具有很强的随机性。关于风速时间序列的预测通常是将其外部特性视为某个单变量的时间序列进行预测。针对风速时间序列的混沌特性，本文考虑将其单变量时间序列作为原始样本，采用混沌相空间重构方法，通过确定一组最佳嵌入维数和延迟时间的方法来实现原始混沌时间序列的相空间重构，获得能够表征原始时间序列动态特性的新的样本空间，继而用神经网络来进行预测，通过对比分析不同的重构样本空间对预测精度的影响，获得最佳的预测模型，能够提高2 h内短期风速的预测精度[1-5]。

1 相空间重构预测方法的基本思想

Takens定理认为系统中任一分量的演化都是由与之相互作用着的其他分量所决定的。对于单变量混沌时间序列，假设预测步数为h，在重构的状态空间中状态的演化就可以用函数F（.）表示，即需要获得如下的非线性函数来实现预测：

其中，函数F（.）可以证明是存在的。

根据Takens嵌入定理可以将单变量时间序列重构成一个相空间，即只要嵌入维数足够高（一般要求m≥2D+1，D为吸引子维数），就可以在拓扑等价的意义下恢复原来的动力系统。对实际观测的时间序列，其中，τ为初始数据的采样间隔，时间序列的长度为l+1.相空间重构的思想就是确定其最佳的嵌入维数m和延迟时间nτ，经过延迟坐标重构获得坐标向量 X（k）={x（k），x（k+nτ），…，x[k+（l+n-mn）τ]}T，从重构的状态空间中可以无歧义的恢复原系统的吸引子特征。样本空间的变化过程如下：

初始混沌时间序列

x（1），x（1+ τ），…，x（k），x（k+ τ），…，x（l）那么本文设计的h步直接预测示意图如图1所示，在上面生成新的样本空间后，将上述矩阵中的数据作为神经网络的训练样本。当预测的精度满足要求后，预测下若干时刻的数据。

图1 h步风速预测示意图

2 基于神经网络预测的基本原理

神经网络是对人类大脑的一种物理结构上的模拟，从结构和功能上模拟人脑的某些功能。数学上已经证明[6-7]，神经网络具有万能函数逼近的特性，能实现任意L2范数上的非线性映射，可有效地解决数据本身模式特征不明确，数据模糊或含噪声的非线性函数拟合问题，本文采用多层前馈神经网络进行风速的建模和预测，其输入输出结构见图2.

图2 基于神经网络的h步风速预测

建模和预测性能效果的评价指标见表1.

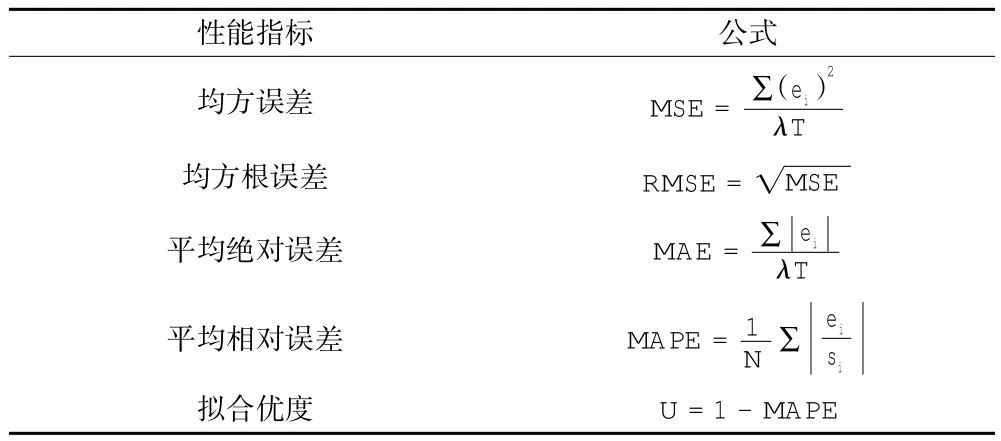
表1 评价指标

3 基于相空间重构的风电场短期风速预测

3.1 数据来源

本文以武隆兴顺风电场连续的2 872组风速时间序列为依据进行分析，如图3所示，预测下若干小时内的短期风速，样本的采样间隔是10 min.

图3 风速时间序列

3.2 神经网络模型预测方法

结合相空间重构理论得到最佳嵌入维数m=3，延迟时间为τ=1.为了全面地考察风速时间序列的动态特性，首先选择风速相空间重构的嵌入维数m在3，4，5 之中，而延迟时间 τ则确定在 1，7，15，18，24，34之间。下面通过将这m和τ进行组合，组合成12组嵌入维数和延迟时间，分别构成不同的样本相空间，利用神经网络进行预测，并通过性能指标来评判预测效果。

在神经网络预测中，输入节点数为相空间重构的嵌入维数m，输出节点数确定为12个，能够连续预测未来若干组风速数据。选择训练步数为500步，误差平方和的性能要求为e-15.经过反复训练后，确定每种神经网络的最佳隐层节点数如表2所示，每种神经网络的预测性能如表3所示。从表中可以看出，在τ=1时，各个维数的预测误差比τ=7，15，18，24，34时要好，从嵌入维数的角度看，在m=3时的预测效果最好。所以，该风速时间序列的最佳嵌入维数m=3，延迟时间为τ=1.此时同时预测了12个未来的风速时间序列值，称为一组。同时，连续预测了12组风速值，预测效果如图4~15所示，图16为三维误差曲面图。从图中可看出，越往后，风速的预测精度越差。表明风速具有时变特性，预测精度受到风速变化速率的制约。对短期风速预测值进行计算，得到该方法预测效果的平均绝对误差为16.2%.利用该方法提高了在此条件下的短期风速时间序列的预测精度。

表2 神经网络结构参数表

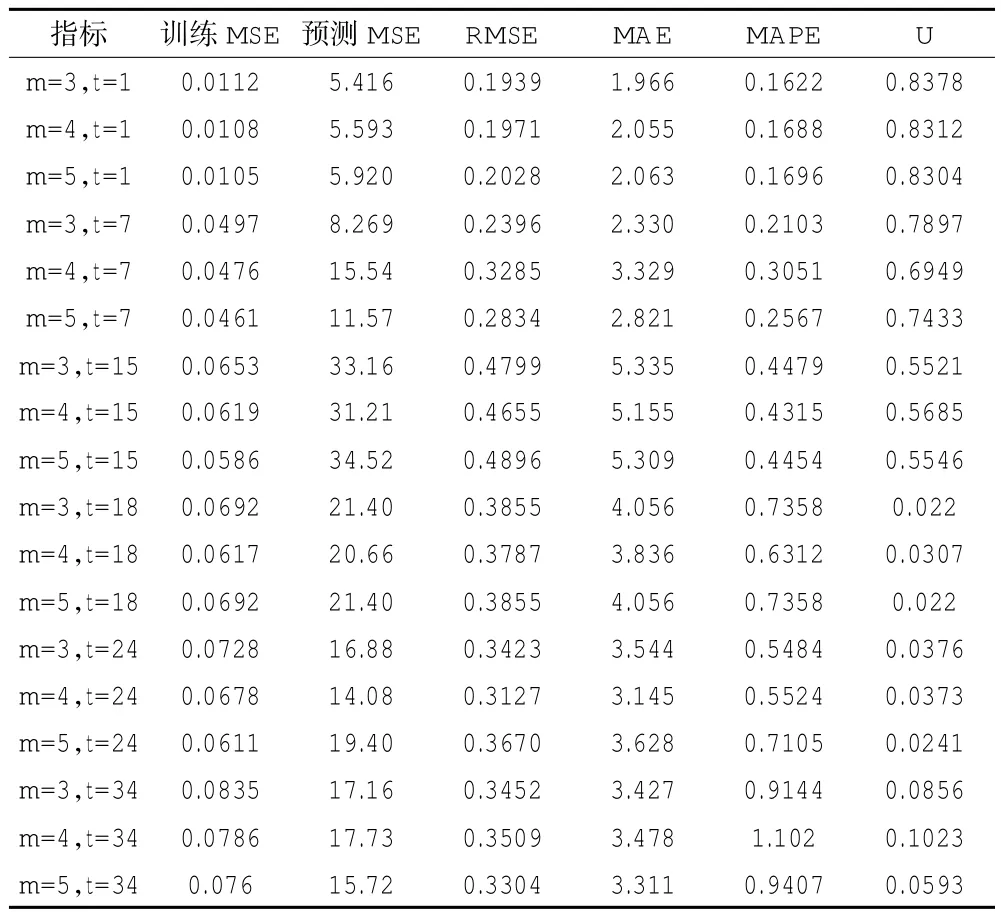
表3 12组的性能指标

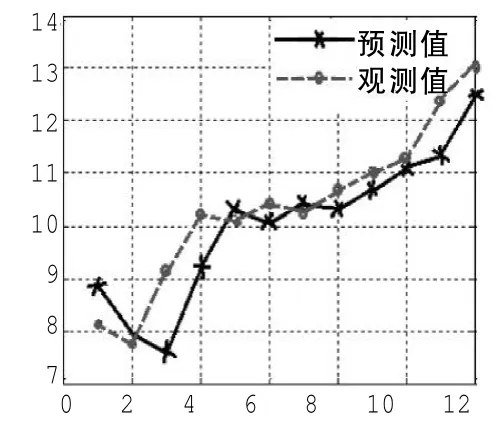
图4 预测第一组

图5 预测第二组

图6 预测第三组

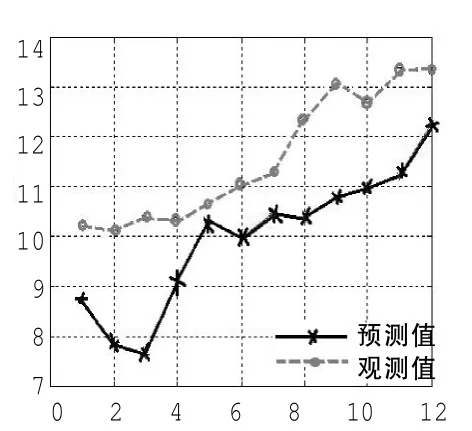
图7 预测第四组

图8 预测第五组

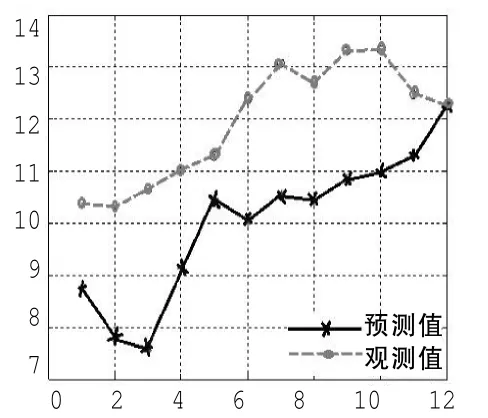
图9 预测第六组

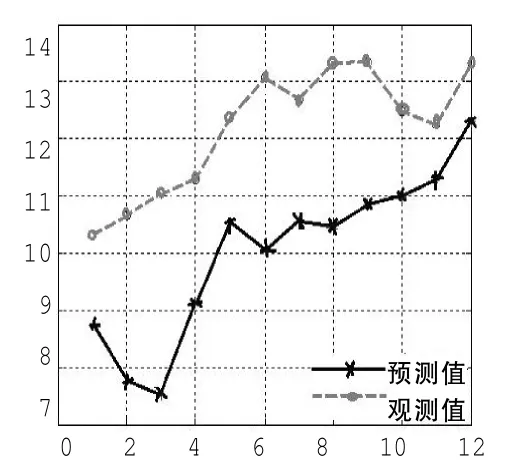
图10 预测第七组

图11 预测第八组

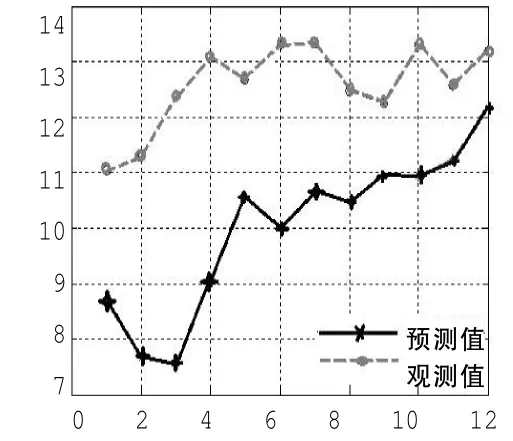
图12 预测第九组

图13 预测第十组

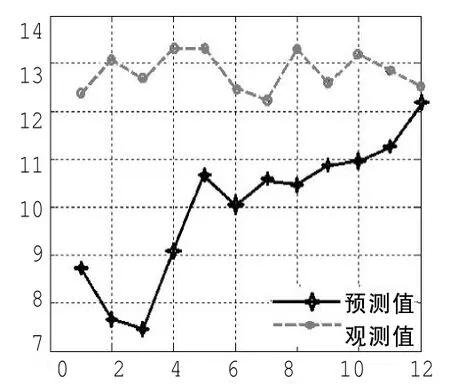
图14 预测第十一组

图15 预测第十二组

图16 三维误差曲面图

4 基于相空间重构的风电场发电功率预测研究

同样对武隆兴顺发电场中，获得的2 872组功率发电数据，进行预测研究。利用第3部分的方法，获得关于发电功率时间序列的嵌入维数为7，延迟时间为1。以此形成的时间序列作为新的神经网络训练数据，建立关于发电功率的预测模型。神经网络的训练过程如上述的方法，得到的训练过程、神经网络的2 872组数据的拟合效果如图17、18、19所示。在表4中列出连续预测的2 h发电功率数值，预测的归一化误差为0.112 4.预测效果较理想。

表4 神经网络预测效果对比表

图17 神经网络性能指标图

图18 拟合效果图

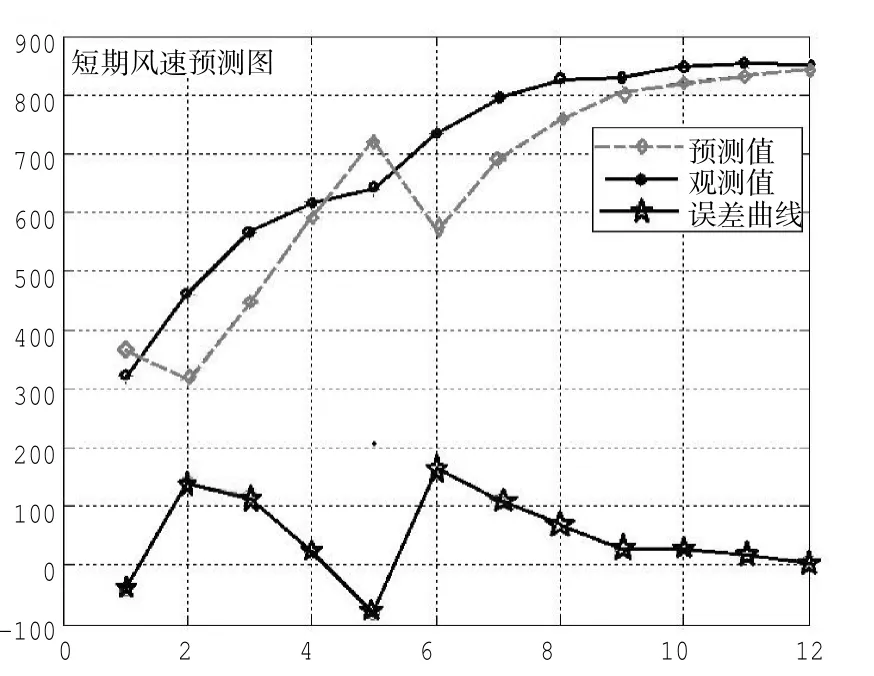
图19 神经网络预测图

5 结束语

针对风电场短期风速和发电功率的预测精度不高的问题，本文将单变量时间序列作为原始样本，采用混沌相空间重构方法，通过确定一组最佳嵌入维数和延迟时间的方法来实现原始混沌时间序列的相空间重构，获得与原时间序列拓扑等价，并且更能体现其混沌特性变化趋势的样本数据，继而用神经网络来进行预测，通过对比分析不同的重构样本空间对预测精度的影响，获得最佳的预测模型，提高了2 h内短期风速的预测精度。下一步，主要研究应集中在算法应用系统开发，并且建立算法扩展平台，为下一步深入研究奠定基础。

[1]韩亚军，李太福，杨小强，等.基于Logistic映射相空间重构神经网络短期风电预测[J].实验技术与管理，2015，32（10）：40-45.

[2]廖志强，李太福，余德均，等.基于相空间重构的神经网络短期风速预测[J].江南大学学报，2012，11（1）：14-18.

[3]HUANG Z,Chalabi Z S.Use of time-series analysis to model and forecast wind speed[J].Journal of Wind Engineering and Industrial Aerodynamics，1995，56（2-3）:311-322

[4]Ergin Erdem,Jing Shi.ARMA based approaches for forecasting the tuple of wind speed and direction[J].APPLied Energy，2011，98（4）:1405-1414.

[5]Rajesh G Kavasseri，Kirthika Seetharaman.Day-ahead wind speed forecasting using f-ARIMA models[J].Renewable Energy.2009，34（5）:1388-1393.

[6]Erasmo Cadenas，Wilfrido Rivera.Short term wind speed forecasting in La Venta,Oaxaca，Mexico,using artificial neural networks[J].Renewable Energy,2009，34（1）:274-278.

[7]Erasmo Cadenas，Wilfrido Rivera.Wind speed forecasting in three different regions of Mexico，using a hybrid ARIMAANN model[J].Renewable Energy，2010，35（12）:2732-2738.