聚焦目标：数学单元检测卷讲评课的用力点

☉江苏省海安市紫石中学 范小震

一、说在前面

当前的数学教学现状下，试卷讲评课是经常出现的，频次较高的周测（有些地方“美名”为周练、周周清），每个单元或章节结束之后的单元检测卷，每月一度的“月考”（有些学校“美名”为阶段调研检测），每学期“常规动作”期中、期末考试等，这些考试之后必然要跟进试卷讲评课，然而这些试卷讲评课该讲评什么？如何讲评？如何准确定位教学重点与难点？教学研究领域似乎对这些的关注还不太多，各级教研活动的课题选择也鲜见开设试卷讲评课的研究，数学教学的重要期刊也少有深入独到的论述.笔者不揣浅陋，对数学单元（或章节）检测卷的讲评提出一些个人的初步思考，供研讨.

二、两种常见讲评现状

讲评现状1：逐题讲评，平均用力，对重点、难点心中缺少预设.

这种现象比较多发生在初任教师身上，他们对于试卷中各道试题的考查目的、内容效度、试题信度和难度的理解还缺少一些专业判断，所以往往是逐题讲评，平均用力，从前往后.根本原因是教师本身对试卷中各道试题的重点与难点理解不深刻，也就难有积极的课前预设，只是满足于各道试题都已解过一遍，在课堂上再帮助学生演算或推证一遍即可，这种平均用力式的试题讲评于大多数优秀学生来说，缺少听课的兴趣，他们往往在这样的试卷讲评课上出现倦怠或拿出其他作业来练习.

讲评现状2：重点问题一带而过，主要精力在讲难题与偏题.

这种现象比较多发生在经验型教师身上，他们认为很多简单的常见题、经典题平时已练习过若干次，不需要在试卷讲评课上再花多少时间进行讲评，而把精力放在试卷上几道难题（有时是偏题与怪题），在这些试题的讲解上呈现不同解法，演算、推出殊途同归的思路，让出错的优秀学生有所收获.这样做确实对少数优秀学生提高应对这类难题的解题能力有好处，但是绝大多数学生会在这种试卷讲评课上不知所云，客观上这些题目确实很难，另一方面，这些试题多数学生在考试时根本就没有时间钻研，待到教师讲评时他们甚至都没有熟悉题意，就很难跟上教师的思路，又要“装出”认真听课的专注模样，结果是该订正的没有时间订正理解，不适合的难题讲评也听不懂，造成这些学生的时间浪费.

比如，最近我们注意到在八年级整式乘除与因式分解的章节检测卷中有如下一些考题：

考题1：已知等腰三角形两边a、b满足a2+b2－4a－10b+29=0，则此等腰三角形的周长为（ ）.

A.9 B.10 C.12 D.9或12

考题2：若（2x＋3）2x+4=1，则x＝_________________.

考题3：先化简，再求值：若（2x＋1）2=24，3x·9y=27，求x+y的值.

考题4：阅读下面的解答过程，求y2＋4y＋8的最小值.

解：y2＋4y＋8＝y2＋4y＋4＋4=（y＋2）2＋4.

∵（y＋2）2≥0，

∴（y＋2）2＋4≥4.

∴y2＋4y＋8的最小值为4.

仿照上面的解答过程，求x2－x+4的最小值和6－2x－x2的最大值.

简评：以上几道试题学生得分率很低，如果讲评时过分纠结于这些试题，则可看成一种本末倒置，这类问题就本章节考试来看，属于剑走偏锋，属于难题、偏题，并不适合所有学生.考题1、考题4都涉及超过现阶段要求的配方法，考题2、考题3对幂的运算性质提出了超过课标和教材的要求.

三、聚焦目标，找准试卷讲评的用力点

1.心中装有“课标”，根据课标要求明确讲评用力点.

有人觉得平时上新授课或研讨课、公开课展示时，听课的人较多，拟写教学目标、辨析教学重点时要注意关注课程标准，试卷讲评课又不是展示课，关注课标做什么？持这种观点的人不在少数.事实上，这既是端正教师本人课程标准规范意识，也是明辨试卷讲评课用力点的重要依据.如果心中对所教单元或章节的教学要求（课程标准上所规定）不甚明了，就会出现像上文中列举的4道难题、偏题大讲特讲，到头来能熟练掌握的学生也不会太多，而对课程标准上要求所有学生都要过关的如幂的运算性质、整式乘除法则、乘法公式、因式分解，缺少必要的讲评与跟进督促.也就是说，明确讲评的重点需要熟知课程标准上的要求，明辨难点则需要对试卷上较难试题进行深入思考，想清难点在哪儿，如何引导优秀学生突破难点.

2.做好测评数据分析，盯紧学生“应知应会”考题.

当前不少学校都有信息化时代下的大数据试卷分析软件，如果能用好这类软件，可以精准定位错题与考生，基于课标规定的一些应知应会考题，分析出多大比例学生出错，哪些学生出现错误，然后对这些试题进行归类讲评，让所有学生在这些试题上过关，错误比例较高的不但要重点讲评，而且要进行变式讲评，利用小组合作学习让学生在小组内过关.有些教师利用让出错的学生讲给组长听，由组长提问答辩等多样化的过关方式，这都是值得肯定的.比如，幂的运算性质的直接运用、整式乘法的法则、乘法公式（平方差公式和完全平方公式），都需要学生人人过关，因为这些内容不仅关乎本章学习目标的达成，更是后续一元二次方程、二次函数学习时的必要基础，尽可能不让一个学生掉队.站在后续初三数学的角度看，对于上文中的考题1、考题4，在学生学习一元二次方程时，会系统学习配方法，到时还会遇到类似的配方问题，所以在初二对用配方法解决问题不宜提出过高的要求.这里也要求单元试卷命题时，命题者心中要有课程标准约束意识，不能随手摘选，不顾课标要求，随意拔高要求，以使被测学生茫然、盲从.

3.针对单元重点考题，跟进变式检测反馈订正效果.

针对单元重点考题讲评之后，需要积极跟进变式检测，以便及时反馈订正效果.如果学生只是满足于简单的修改答案，则面对变式试题不一定能有效解答.作为必要的案例跟进，我们给出一些变式检测的题例，供分享：

考题5：（等腰三角形单元检测卷一道把关题）如图1，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA的延长线上一点，点O是线段AD上一点，OP=OC.证明：

（1）∠APO+∠DCO=30°；

（2）△OPC是等边三角形；

（3）AC=AO+AP.

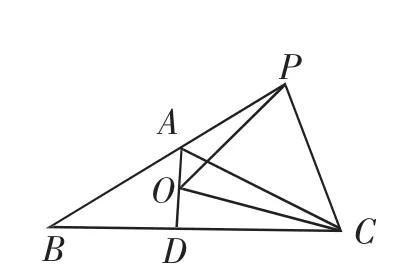
图1

阅卷与讲评：这道考题多数考生只能完成第（1）问，只有几个学生完成了第（2）问，第（3）问只有2个学生证明成功.我们进行了认真讲评，并要求把推证过程整理出来，在第二天，我们又跟进变式如下一道考题进一步检测学生的掌握情况.

变式检测：在等边△ABC外侧作直线AP，点B关于直线AP的对称点为D，连接BD、CD，其中CD交直线AP于点E.连接BE.

（1）补全图1，求证∠ACD=∠ABE.

（2）结合图2、图3，补全图形，猜想∠BEC的度数是否变化.如果不变，求出度数.

（3）分析线段BE、AE、CE的数量关系.

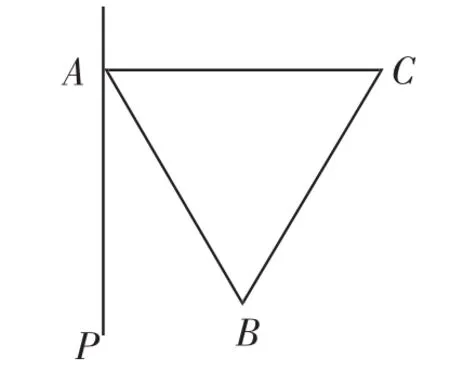
图2

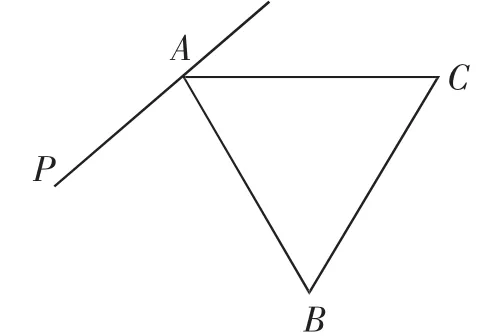
图3

设计意图：前两问对应着原考题的前两问，最后一问源于考题的第（3）问但又高于第（3）问，还需要分类讨论.

4.针对考卷较难试题，点拨思路提示路径鼓励自主钻研.

最后，针对考卷中较难试题（包括偏题、怪题），我们的态度是：教师不能全讲，但也不能不讲.以点拨思路或提示解题路径为主，鼓励学生记录思路后自主钻研，梳理过程、完善解法.因为，从根本上说，很多难题并不是由教师讲懂的，而是经过恰当的点拨或提示，学生自己悟出来的，这样得来的解法往往也能记得更牢、理解得更深.

四、写在最后

试卷讲评课是一个值得深入研究的教研课题，我们提取其中单元检测卷进行了一些初步实践和思考，认识还很初步，也多有个性化理解成分，供大家批判.更欢迎大家关于试卷讲评课结合案例给出观点阐释，分享试卷讲评的经验，促进试卷讲评课的效益提升.

1.储秀梅.同类跟进：试卷讲评课的一种策略——以一道反比例函数把关题讲评为例［J］.中学数学（下），2017（5）.

2.潘龙生.教学，少些一带而过［J］.数学通报，2015（1）.

3.王成.同类链接促进感悟，模考讲评提升效益——以一次模考题的链接讲评为例［J］.中学数学（下），2017（2）.F