多分量调幅-调频信号的瞬时频率 直接计算与畸变消除方法
2018-06-21贾林山张庆
贾林山,张庆,2
(1.西安交通大学机械工程学院,710049,西安; 2.西安交通大学现代设计及转子轴承系统教育部重点实验,710049,西安)
瞬时频率是调幅-调频(AM-FM)信号的重要调制参数,对于探究非平稳、非线性过程的信息表征机制具有重要意义[1]。然而,由于调频造成的频域复杂性,传统的基于稳态频谱分离的解调技术无法获得准确的瞬时频率,因此研究瞬时频率的求解方法具有重要意义。目前,有许多瞬时频率求解方法,包括应用于经验AM-FM分解中的直接正交法(DQ)与归一化Hilbert变换法(NHT)[1]、应用于Hilbert-Huang变换中的Hilbert变换法(HT)[2]、应用于LMD中的直接计算法[3]、Teager能量算子法[4]等,近年来,复域能量算子解调法[5]等一些新的瞬时频率求解方法也相继被提出。
基于LMD的直接计算法是一种性能良好的瞬时频率计算方法,具有不会出现难以解释的负频率、无明显的端点效应等优点[6],目前已经成功应用于脑电信号分析[3]、转子碰磨故障诊断[5]、齿轮和轴承故障诊断[7]、颤振识别[8]等领域。但是该方法也存在一些问题,首先通过反余弦函数求解得到的瞬时相位不是单调的,为获得正的瞬时频率,需要将之展开为单调递增的瞬时相位,该步骤较为复杂,使得直接计算法的运行效率较低;其次,直接计算法求得的瞬时频率在对应于纯调频信号极值点附近位置总是不可避免地存在较大的计算误差,在瞬时频率曲线上表现为明显的畸变[9]。
针对直接计算法进行相位展开而导致的低效率的问题,本文提出了一种快速直接计算法,不需要进行相位展开,运行效率更高。针对直接计算法求取的瞬时频率存在的畸变问题,本文提出了一种畸变定位与消除算法,可以较好地识别出畸变的发生位置,然后将畸变位置处的瞬时频率剔除,最后使用三次样条插值补全被剔除的数据,得到无畸变的瞬时频率。
1 快速直接计算法
局部均值分解(LMD)是由英国学者Jonathan S.Smith在2005年提出的一种针对多分量AM-FM信号的解调方法[3],能自适应地将一个复杂的多分量AM-FM信号分解为若干个乘积函数(PF)分量之和,其中每一个PF分量是一个包络信号和一个纯调频信号的乘积[3],包络信号就是该PF分量的瞬时幅值(IA),而PF分量的瞬时频率(IF)可由纯调频信号求出,从而实现对多分量AM-FM信号的解调。
文献[3]在介绍LMD方法的同时,引入了直接计算法来计算每一个PF分量的瞬时频率。设LMD分解得到的某一PF分量由包络函数a(t)和纯调频信号s(t)相乘得到,即
PF(t)=a(t)s(t)
(1)
则PF的纯调频信号s(t)可以写为一个余弦函数的形式,即
s(t)=cosφ(t)
(2)
那么瞬时相位φ(t)可以写为纯调频信号s(t)的反余弦,且瞬时频率f(t)通过瞬时相位直接求出,即
(3)
反余弦函数是定义在区间[-1,1]上的单调递减函数,而纯调频信号一般为非单调函数,则瞬时相位φ(t)就不再是单调函数,因此如果直接按照式(3)求解f(t),将会产生负频率。为解决这一问题,文献[6]推导出了将非单调的瞬时相位整体展开为单调递增瞬时相位的基本步骤,文献[3]提出将波形分段,在一个全波内将相位展开。这两种方法都需要将相位展开,运行效率较低。
相位展开的实质就是将原本非单调的瞬时相位序列中的递减部分序列变换为递增序列,这一过程对于式(3)来讲,由单调递增的展开相位和非单调的未展开相位求得的瞬时频率f(t)在负频率部分恰好互为相反数,因此相位展开(无论是分段相位展开还是全局相位展开)并不是保证最终求得的瞬时频率为正的必要条件。基于以上分析,本文提出一种快速直接计算法,具体步骤如下。
(1)设乘积函数PF的纯调频信号为s(t),为保证s(t)所有取值在反余弦函数定义域内,将s(t)的所有极大值点置为1,所有极小值点置为-1,然后将s(t)所有大于1的点置为1,所有小于-1的点置为-1,最终使s(t)满足-1≤s(t)≤1。将调频信号s(t)取反余弦,得到非单调的瞬时相位
φ(t)=arccoss(t)
(4)
(2)对非单调的瞬时相位φ(t)进行前向差分,设信号采样频率为fs,得到包含有负瞬时频率的初始瞬时频率
(5)
式中:diff表示后向差分运算。
(3)对初始瞬时频率f0(t)取绝对值,得到全部为正值的瞬时频率
f1(t)=|f0(t)|
(6)
通过相位展开获得单调递增的瞬时相位这一过程是为满足瞬时频率须由单调递增的瞬时相位差分得到这一数学定义,但是从计算角度来说,相位展开与否并不影响求得的瞬时频率的绝对值,因此可以免去不必要的相位展开计算,在不影响结果的前提下,获得更高的计算效率。
需要说明的是,此时f1(t)中不可避免地存在大量畸变点,其原因是:将反余弦函数的导数代入式(3)中得到
(7)
当s(t)接近于1时,分母接近于0,使得s′(t)的误差被放大[10],从而在极值点附近产生畸变。该畸变具有孤立出现、幅值大幅变化的毛刺状特点,使求解出的瞬时频率不可直接使用。
2 直接计算法畸变定位与消除算法
使用直接计算法得到的瞬时频率在对应于纯调频信号极值点附近总是存在毛刺状畸变点,必须要经过消除毛刺处理才能得到可用的瞬时频率,通常采用中值滤波法[1]、滑动平均法[6]、形态学滤波法[11]等用于消除畸变。然而,上述方法存在3点问题:首先,对瞬时频率畸变位置的出现规律缺乏深入探究;其次,采取的方法需要一定的先验知识,比如,如何选择滑动步长和平滑次数,如何选择形态学滤波的结构元素形状和长度等;第三,在处理瞬时频率的畸变点时,不可避免地对非畸变点产生影响,即不具备局部处理特性。
为此,对畸变的出现位置进行分析,发现畸变均位于极值点附近,根据极值点处采样点分布的不同,可以分为三角分布型和梯形分布型2大类。选取纯调频信号s(t)的极值点以及左右两侧各两个采样点构成一个5点区域,对区域内各点根据幅值进行降序排序,分别为D1~D5,则出现以下两种情况:
(1)如果D3点幅值绝对值更靠近D2,则为三角分布型,若D3点在D2左侧,则D1和D2是畸变点;若D3点在D2右侧,则D1和D3是畸变点。
(2)如果D3点幅值绝对值更靠近D4,则为梯形分布型,若D3点在D2左侧,则D1、D2和D4是畸变点;若D3点在D2右侧,则D1、D2和D3是畸变点。
设计畸变定位与消除算法,具体步骤如下。
(1)设乘积函数PF的纯调频信号为s(t),为保证s(t)所有取值在反余弦函数定义域内,将s(t)的所有极大值点置为1,所有极小值点置为-1,并将s(t)中大于1的点置为1,小于-1的点置为-1,使s(t)满足-1≤s(t)≤1。
(2)找出信号s(t)的第一个极值点E1,将s(t)的极值点位置及其两侧各2个采样点位置共计5个点按幅值的绝对值大小进行降序排序,分别标识为D1~D5,其对应采样时刻分别为tD1~tD5。
(3)设Z=|s(tD3)-s(tD2)|-|s(tD4)-s(tD3)|。那么如果Z<0,为三角分布型,若tD3 如果Z>0,为梯形分布型,那么若tD3 (4)处理完第1个极值点E1后,再对下一个极值点重复进行步骤(1)~(4),直至所有的极值点都被处理完成,输出畸变位置序列T。 (5)将带有毛刺的瞬时频率f1(t)在毛刺位置序列T处的数据删除,并使用三次样条插补出毛刺位置序列T处的瞬时频率值,最终可以得到无毛刺的瞬时频率f(t)。 上述算法要求纯调频信号s(t)的每一个全波至少应有6个采样点,因此本文提出的毛刺定位算法对采样频率具有适用性条件,即采样频率不得低于s(t)中最高瞬时频率的6倍。同时,从上述算法畸变定位结果来看,在一般情况下,每一个极值点位置一般有2~3个畸变点,即高于1/6~1/4采样频率的瞬时频率可能无法由直接反余弦法正确解出。 考察由两个AM-FM分量组成的仿真信号 x(t)=(1+0.5cos(8πt))cos(200πt+ 2cos(10πt))+0.8sin(πt)sin(30πt), t∈[0,1] (8) 设定采样频率为1 024 Hz,其时域波形见图1。 图1 仿真信号x(t)的时域波形图 为了提取两个分量的瞬时频率,首先需要采用LMD方法对x(t)进行分解,得到两个PF分量和1个余项R,如图2所示。从图2中可以看出,x(t)中的两个AM-FM分量分别对应前两个PF分量。 为比较本文提出的快速直接计算法和传统的基于相位展开的直接计算法[6]的运行效率,分别使用两种方法求解PF1分量的纯调频信号s1(t)的瞬时频率。在相同计算机环境下,连续运行5次,记录运行时间如表1所示,最终取平均值得到二者平均运行时间之比为25.748 2。即针对本例,本文提出的快速直接计算法的运行效率大约是基于相位展开的直接计算法的25倍左右,速度优势较为明显。 图2 仿真信号x(t)的LMD分解结果 表1 两种方法运行时间的比较 基于相位展开的直接计算法得到s1(t)的瞬时频率如图3所示,本文提出的快速直接计算法得到s1(t)的瞬时频率如图4所示,二者波形一致。 图3 基于相位展开的直接计算法得到的瞬时频率 图4 本文方法得到的瞬时频率 从图4中可见,直接计算法求得的瞬时频率存在大量毛刺状畸变点,为保证结果有效,需要把这些畸变点去除。按照第2节提出的畸变定位与消除算法对使用本文算法求得的存在畸变的瞬时频率进行定位和消除。首先将所有的畸变点定位,使用“*”标识出了所有的畸变点位置,如图5所示。然后,将畸变点位置数据剔除,使用三次样条插值将畸变点位置数据补全,最终得到s1(t)的IF曲线如图6所示。从图6中可以看出,原本布满毛刺的IF曲线中的畸变点被有效去除。 图5 畸变点定位标识 图6 去除畸变后的瞬时频率 使用Hilbert变换对s1(t)求解瞬时频率,即归一化Hilbert变换[1],得到IF曲线如图7所示。 图7 使用归一化Hilbert变换求取的s(t)的瞬时频率 对比图6和图7,两者形状基本相近,均存在一定波动,也即由LMD对信号x(t)分解得到的PF1分量的纯调频信号中实际的瞬时频率确实如图6和图7所示的那样,存在不平滑的波动,这种波动是由于LMD分解过程中的误差导致的,而不是由信号提取方式(NHT或直接计算法)导致的。 为更深入地说明该问题,使用滑动平均法[12]对带有畸变点的瞬时频率进行平滑,这里设定滑动步长为5,滑动平均次数为10,得到的结果如图8所示。 图8 使用滑动平均法处理畸变后的瞬时频率 图8与图7相比看起来更加平滑和精确,但在平滑畸变点的过程中,LMD本身的分解误差也被平滑而丢失了。本文方法是仅将畸变点去除,然后使用插值补全,未对非畸变位置数据进行修改,在选择性剔除畸变点的同时,完整地保留了LMD自身分解误差导致瞬时频率波动,具有局部处理的特性,这是本方法与传统的如滑动平均、形态学滤波、中值滤波等全局处理方法的一个重要的不同之处。此外,识别畸变点位置是全部无参数的,不依赖于使用者的经验,这也是本文方法的重要优势。 为进一步验证本文方法的有效性,以某烟气轮机碰磨故障的转子位移信号为例进行分析。烟气轮机工作转速为446 r/min,工作频率为7.43 Hz,信号采样频率为200 Hz,其信号波形如图9所示。 图9 烟气轮机转子碰磨信号时域波形 当发生碰磨故障时,转子位移信号为多分量AM-FM信号,其中的每一个分量都是由工频的倍频为载频,以工频为调制频率的具有物理意义的单分量AM-FM信号。从理论上来讲,只要求出其中某一个单分量AM-FM信号的瞬时频率,并对瞬时频率作幅值谱,便可找到蕴藏在信号中的频率调制信息,实现转子碰磨的故障诊断。为此使用LMD将信号分解,得到3个PF分量和1个余项,如图10所示。 图10 转子碰磨信号的LMD分解结果 使用本文方法对得到的PF分量求解瞬时频率,发现PF2对应的瞬时频率在二倍频附近周期性波动,如图11所示。为得到确切的调频频率,分析PF2对应的瞬时频率的幅值谱,如图12所示。从图12可以看出,幅值谱主峰为工频,即PF2中存在频率调制,其调制频率为工频,即PF2瞬时频率曲线中周期性波动的频率为工频,因此可以判断烟气轮机转子发生了碰磨故障,与实际情况相符。 图11 PF2纯调频信号的瞬时频率 图12 PF2纯调频信号的瞬时频率的幅值谱 瞬时频率在语音信号分析领域具有广泛应用[13]。为进一步说明本文方法的适用性,以语音信号为例进行分析。 使用声音传感器在48 kHz采样率下采集双元音/ei/的声音信号,发音者为男性,保存为wav格式,波形和频谱如图13所示。 (a)语音信号 (b)信号频谱图13 双元音/ei/语音信号及信号频谱 截取0.3~0.4 s的语音信号进行LMD分解,得到6个PF分量,其中前3个PF分量如图14所示。 图14 双元音/ei/语音信号的LMD分解结果 经过分析发现,PF1分量主要为高频噪声,而PF2分量保留了原始信号中的大部分能量,从PF2分量波形可以看出符合元音具有周期性脉冲的特点,脉冲的间隔周期的倒数即为基音频率。将PF2作为分析对象,使用本文方法分析其纯调频信号的瞬时频率,如图15所示。 图15 PF2纯调频信号的瞬时频率 图16 PF2纯调频信号瞬时频率的幅值谱 从图15可以发现,PF2的瞬时频率在第1个共振峰中心频率f1附近波动,瞬时频率的幅值谱如图16所示。从图16可以看出,频谱中存在最高谱峰,对应频率为基频154 Hz,即PF2中信号瞬时频率以154 Hz频率波动,从而有效提取出该语音信号中的基音频率。 本文研究了一种瞬时频率快速直接计算方法,并针对该方法求得的瞬时频率存在大量畸变点的问题,提出了一种无参数的畸变定位与消除算法,得到了如下结论。 (1)在保证和传统的基于相位展开的瞬时频率的直接计算法的结果一致的情况下,提出的瞬时频率快速直接计算方法运行效率更高,算法更加简单。 (2)与传统的畸变消除方法相比,本文的畸变定位与消除算法具有无参数、局部处理的优势。 (3)本文提出的瞬时频率快速直接计算法和畸变与定位消除算法可以得到正的、有物理意义的瞬时频率,并成功用于机械故障诊断与语音信号基音频率识别。 参考文献: [1] HUANG N E,WU Zhaohua,LONG S R,et al. On instantaneous frequency [J]. Advances in Adaptive Data Analysis,2009,1(2): 177-229. [2] HUANG N E,SHEN Z,LONG S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society: A Mathematical,Physical & Engineering Sciences,1998,454(1971): 903-995. [3] SMITH J S. The local mean decomposition and its application to EEG perception data [J]. Journal of the Royal Society Interface,2005,2(5): 443-454. [4] MARAGOS P,KAISER J F,QUATIERI T F. On amplitude and frequency demodulation using energy operators [J]. IEEE Transactions on Signal Processing,1993,41(4): 1532-1550. [5] ZENG M,YANG Y,ZHENG J. et al. Normalized complex Teager energy operator demodulation method and its application to fault diagnosis in a rubbing rotor system [J]. Mechanical Systems and Signal Processing,2015(50/51): 380-399. [6] 任达千,杨世锡,吴昭同,等. 信号瞬时频率直接计算法与Hilbert变换及Teager能量法比较 [J]. 机械工程学报,2013,49(9): 42-48. REN Daqian,YANG Shixi,WU Zhaotong,et al. Comparison of instantaneous frequency directed computing method and Hilbert transform and Teager energy method [J]. Journal of Mechanical Engineering,2013,49(9): 42-48. [7] 张亢,程军圣,杨宇,等. 基于分段波形的信号瞬时频率计算方法 [J]. 湖南大学学报(自然科学版),2011,38(11): 54-59. ZHANG Kang,CHENG Junsheng,YANG Yu,et al. A piece-wise based signal instantaneous frequency computing method [J]. Journal of Hunan University (Natural Sciences),2011,38(11): 54-59. [8] SUN H,ZHANG X,WANG J. Online machining chatter forecast based on improved local mean decomposition [J]. International Journal of Advanced Manufacturing Technology,2016,84(5/6/7/8): 1045-1056. [9] 陈保家,何正嘉,陈雪峰,等. 机车故障诊断的局域均值分解解调方法 [J]. 西安交通大学学报,2010,44(5): 40-44. CHEN Baojia,HE Zhengjia,CHEN Xuefeng,et al. Locomotive fault diagnosis based on local mean decomposition demodulating approach [J]. Journal of Xi’an Jiaotong University,2010,44(5): 40-44. [10] 任达千. 基于局域均值分解的旋转机械故障特征提取方法及系统研究 [D]. 杭州: 浙江大学,2008: 31-32. [11] 唐贵基,王晓龙. LMD的LabVIEW实现及其在齿轮故障诊断中的应用 [J]. 中国测试,2014,40(1): 101-105. TANG Guiji,WANG Xiaolong. LMD realization by LabVIEW and its application in gear fault diagnosis [J]. China Measurement & Test,2009,43(3): 523-528. [12] 任达千,杨世锡,吴昭同,等. 基于LMD的信号瞬时频率求取方法及实验 [J]. 浙江大学学报(工学版),2009,43(3): 523-528. REN Daqian,YANG Shixi,WU Zhaotong,et al. Instantaneous frequency extraction method and experiment based LMD [J]. Journal of Zhejiang University (Engineering Science),2009,43(3): 523-528. [13] SCHLOTTHAUER G,TORRES M E,RUFINER H L. A new algorithm for instantaneousF0,speech extraction based on ensemble empirical mode decomposition [C]//European Signal Processing Conference. Piscataway,NJ,USA IEEE,2015: 2347-2351.3 仿真信号分析






4 试验信号分析
4.1 转子碰磨故障诊断



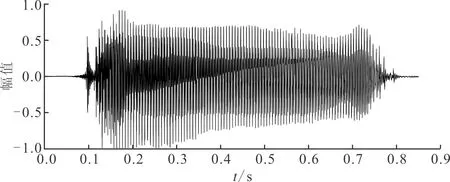
4.2 语音信号分析




5 结 论
