按类统计方法在滚动轴承可视化 可靠性动态评估中的应用

孟文俊,张四聪,淡紫嫣,刘弹,徐光华,2

(1.西安交通大学机械工程学院,710049,西安; 2.西安交通大学机械制造系统工程国家重点实验室,710054,西安)

机械设备在运行过程中一旦某个零部件发生故障,往往会影响整个机械设备的性能,有可能造成巨大的经济损失[1-3],而滚动轴承是旋转机械中关键的零部件,其可靠性与寿命直接影响设备的使用寿命和运行可靠性[4]。因此,开展运行性能可靠性的研究,确保设备安全运行和预防事故发生是十分必要的。

滚动轴承运行性能可靠性评估的核心问题是从大量的性能指标序列中提取稳定的退化轨迹,建立滚动轴承性能指标的概率模型,从而对轴承的退化程度进行评判。传统研究主要采用基于失效规律和统计学的运行性能可靠性评估。Lu等人假设机械设备的性能指标服从正态分布,通过计算分布函数中超过失效阈值的部分,实现单个设备可靠性的评估[5]。西安交通大学丁峰等人把表征设备退化状态的特征值和传统可靠性的统计模型与比例故障率模型进行结合,实现了滚动轴承可靠性的评估[6]。Nelson假设设备性能指标的对数服从一种分布均值随时间变化、而方差随时间不变的正态分布,通过该分布模型进行滚动轴承可靠性的评估[7]。

利用统计学进行可靠性评估的方法可以得到滚动轴承性能退化一般规律性的认识,但是传统可靠性评估方法中的分布模型是一个需要先验知识的静态模型,需要大量的试验数据和先验知识对统计模型的参数进行修正,不会随运行时间的变化自适应调整。这种参数化的统计模型需要明确滚动轴承退化规律的分布形式,对于在运行中的滚动轴承而言是难以实现的。

滚动轴承在寿命周期中,空间状态并不连续,当轴承逐渐退化,稳定性逐渐减弱,可靠性逐渐下降,其空间状态发生跃迁,概率模型的类别会逐渐增多。在国内外研究中,均方根和峭度通常被用作滚动轴承寿命评估指标[8-11],所以本文以滚动轴承的均方根和峭度为分析对象,基于核密度法建立了动态按类概率模型,转化为能够直观显示滚动轴承退化状态的按类概率图像模型,并在按类概率图像模型中计算非正常类的图像分布区域面积占总图像分布区域面积的比值,得到可靠性指标。通过分析样本的不断积累扩充进行模型更新,建立起动态可调的可视化按类概率图像模型。概率图像模型的类别数目用于判断轴承的退化过程,得到的可靠性指标能够反映轴承的退化程度。

1 滚动轴承动态按类概率图像模型

将实时获取的预处理后的性能指标数据作为研究对象,建立动态可调的按类统计概率模型,实现滚动轴承退化状态的准确描述。为了使用多维性能指标序列建立包含更多信息的按类概率模型来反映滚动轴承的运行状态,本文提出了一种基于按类统计的滚动轴承可视化可靠性动态评估方法,具体流程如图1所示。

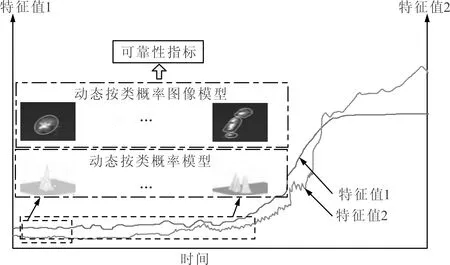
图1 基于按类统计的滚动轴承可视化可靠性动态评估流程

(1)通过性能指标序列获取正常运行时刻的统计样本,建立基于核密度法的初始按类概率模型,该类样本为正常类。

(2)将初始按类概率模型进行可视化处理,得到初始按类概率图像模型,且确定分类边界线。

(3)提取按类概率图像模型中的统计指标故障率,并计算可靠性指标。

(4)当有新性能数据时,根据分类边界线进行类别判断,建立新类别的概率图像模型,并确定每类的分类边界线,提取可靠性指标。

(5)随着分析样本的不断累积,得到不同类的样本,使按类概率图像模型和可靠性指标不断更新,实现滚动轴承可靠性的动态评估。

1.1 基于核密度法的动态按类概率图像模型

核密度法是一种根据数据本身研究其分布特征的非参数估计法[12]。由于滚动轴承性能指标的原始概率密度分布是未知的,因此可以使用核密度法估计概率密度分布,消除随机因素对概率密度分布的影响。

假设X={x1,x2,…,xm}为观测数据序列,用核函数运算得到每个样本点处的概率密度函数

(1)

式中:p为样本维数;σ为平滑因子;

对m个样本点的概率密度分布曲线进行叠加,可以逼近设备原始状态的概率密度分布

(2)

通过式(1)和式(2)可知,平滑因子就是该概率密度函数的标准差,对概率密度分布有重要影响。如果平滑因子σ选择过大,使概率密度分布曲线变得平滑,不能很好地表达细节信息;如果σ过小,噪声信息会对概率密度分布产生影响,无法有效识别有用信息中的噪声干扰。

Cain通过大量实验研究和对比发现,平滑因子与样本间平均最小距离有关[13]。样本点间的平均最小距离为

i,j=1,2,…,m;i≠j

(3)

在计算样本点之间距离时,当距离小于给定阈值(本文中取为0.001)时,认为两个样本点为同一个点。平滑因子可表示为

σ=gd

(4)

式中:g=1.1～1.4。

为了更准确地描述滚动轴承的退化状态,对样本进行类别划分,建立动态按类概率图像模型,建立的流程如图2所示。

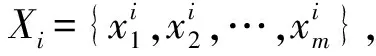
(5)

将不同类的概率模型进行叠加,得到这一观测时刻的按类概率模型

(6)

为了便于按类概率模型动态调整与图形化显示,式(5)在使用中并没有除以加和前面的系数m。

在第k+1次观测时,对新数据进行类别判断,更新按类概率图像模型。

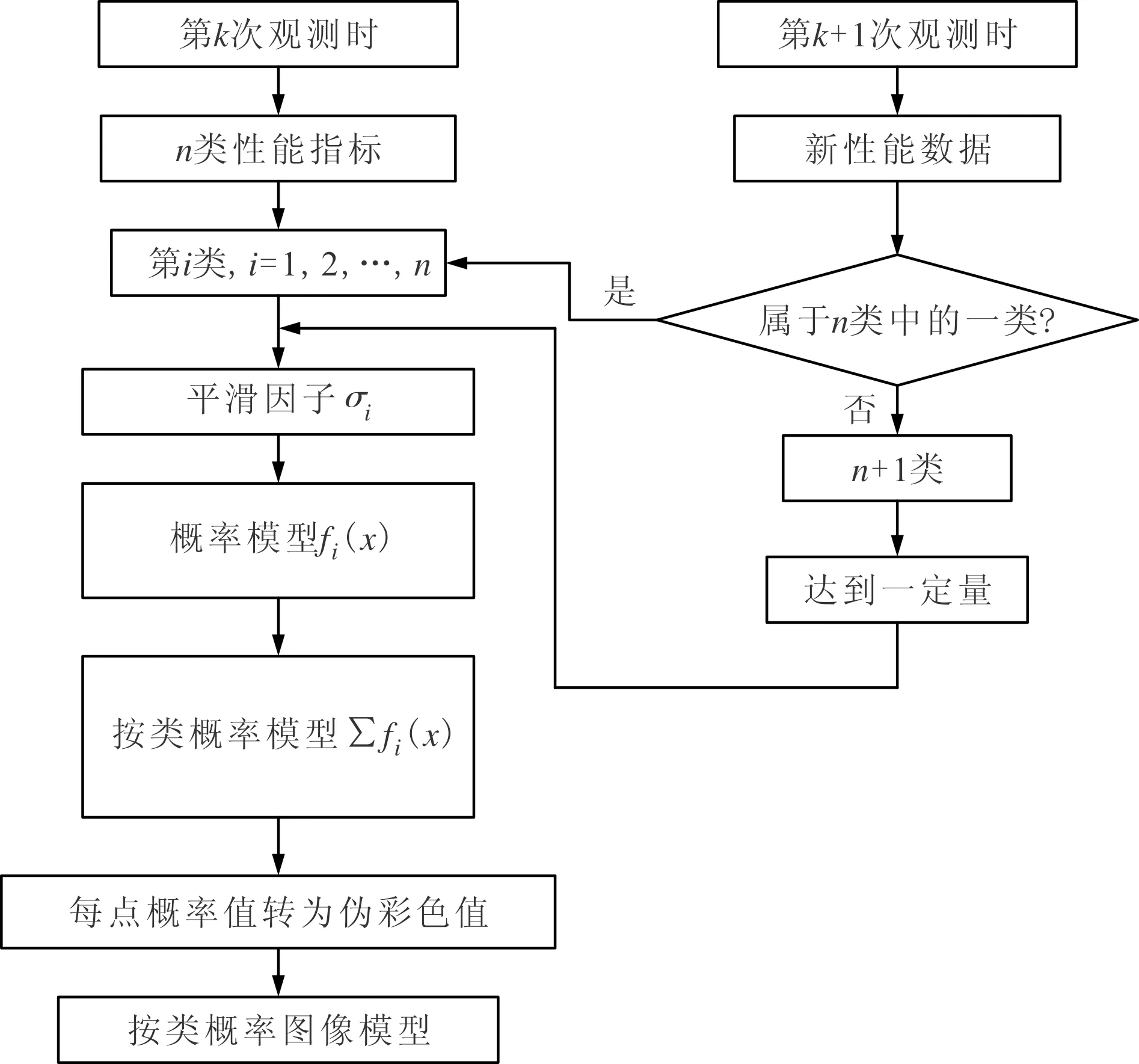
图2 动态按类概率图像模型的建立流程

1.2 基于拉依达准则确定分类边界线

本文通过拉依达准则确定不同类别之间的分类边界线[14]。新样本点落在(μ-3σ,μ+3σ)之外的概率仅为0.27%,在概率统计中认为是小概率事件,因此图像模型中3σ处的概率值即为分类边界线。

利用同类数据计算的平滑因子带入该类单一样本点的概率密度函数计算中,得到图3所示的概率模型是一个以样本点为中心的对称图形。在单一样本点的概率密度分布曲线中,与中心距离相同的点只保留一个值,得到图4所示的截面数据曲线。

图3 单一样本点的概率密度分布曲线

图4 截面数据曲线

通过同类数据得到一个平滑因子σ,就可以确定一个类的概率图像模型,通过对比新样本点的概率与3σ处的概率,可以判断新样本点是否属于这一类。求取新性能数据在图像模型中的概率采用双三次插值法[15]。判断指标如下

p=pnew-pbie

(7)

式中:p为判断指标;pnew为新样本点处概率值;pbie为分类边界处的概率值。

当p≥0,说明该样本点在(μ-3σ,μ+3σ)范围内,属于本类;当p<0,新样本点的概率小于边界处的概率,即新样本点超出了(μ-3σ,μ+3σ)的范围。新性能数据为非本类数据,此时产生了新的概率密度分布类型,说明此时滚动轴承的稳定性有所下降。当每类的统计样本更新时,平滑因子、分类边界线也在不断更新。

2 滚动轴承可靠性的动态评估

在获取滚动轴承一定量正常统计样本的基础上,得到可靠性指标,实现滚动轴承可靠性的动态评估,具体流程如图5所示。

图5 滚动轴承可靠性动态评估流程

(1)本研究中的可视化按类概率模型是三维模型,所以以二维性能指标序列为基础,获取滚动轴承的振动数据,提取其均方根和峭度性能指标。

(2)由于不同维数据的离散程度会对概率模型产生影响,为了减小不同维数据离散程度的不一致性,对均方根和峭度指标进行如下的预处理

(8)

(3)获取正常状态下一定量的二维性能指标数据作为统计样本,称为正常类

(9)

(4)根据式(3)和式(4)计算正常类平滑因子,利用核密度法计算该类每个样本点的概率密度分布曲线,并对m个样本点的概率密度分布曲线进行叠加,得到初始按类概率模型

(10)

(5)将初始按类概率模型进行可视化,得到按类概率图像模型,并确定分类边界线。

(6)在按类概率图像模型中,通过大于该类3σ概率的像素点数来估计每类图像的分布区域面积。根据按类概率图像模型中非正常类的图像分布区域面积占总图像分布区域面积的比值得到故障率,根据故障率计算出可靠性指标如下

(11)

式中:h(t)为故障率函数。

(7)当有新数据时,根据判断指标p更新可靠性评估指标。p≥0时认为新数据为正常类数据,p<0时将新数据作为另外一类。当这类中的样本累加到一定量(本文设为5个)时,根据计算的平滑因子建立该类的概率模型,并确定分类边界线。重复步骤(6)得到新的可靠性指标。一般来说,随着轴承运行时间的增加,轴承可靠性降低,概率图像模型的类别会逐渐增加。

(8)当又有新数据时,根据每类的分类边界线进行类别判断,属于某一类就加入,不属于其中一类就另成一类。通过数据的不断积累,重复步骤(7),得到不同的按类概率图像模型,从而得到不同时刻的可靠性指标。

3 实验验证

3.1 数据来源及说明

本文使用美国智能维护系统中心提供的滚动轴承寿命实验数据进行分析。滚动轴承参数见表1。

表1 实验轴承参数表

给定负载为27 kN,转速为2 000 r/min。在每个轴承的轴承座上安装PCB 353B33型加速度传感器,通过6062E型数据采集卡每隔10 min对图6中滚动轴承1进行信号采集,采样频率为20 kHz,采样点数为20 480。轴承寿命为164 h,在寿命末期发生外圈故障。

图6 滚动轴承寿命实验装置

3.2 滚动轴承的动态按类概率图像模型

(1)性能指标的选取。将预处理后原始振动信号的均方根和峭度作为性能指标,得到滚动轴承运行115 h的特征指标变化,如图7所示。

图7 预处理后特征值变化趋势

(a)33 h

(b)91 h

(c)115 h

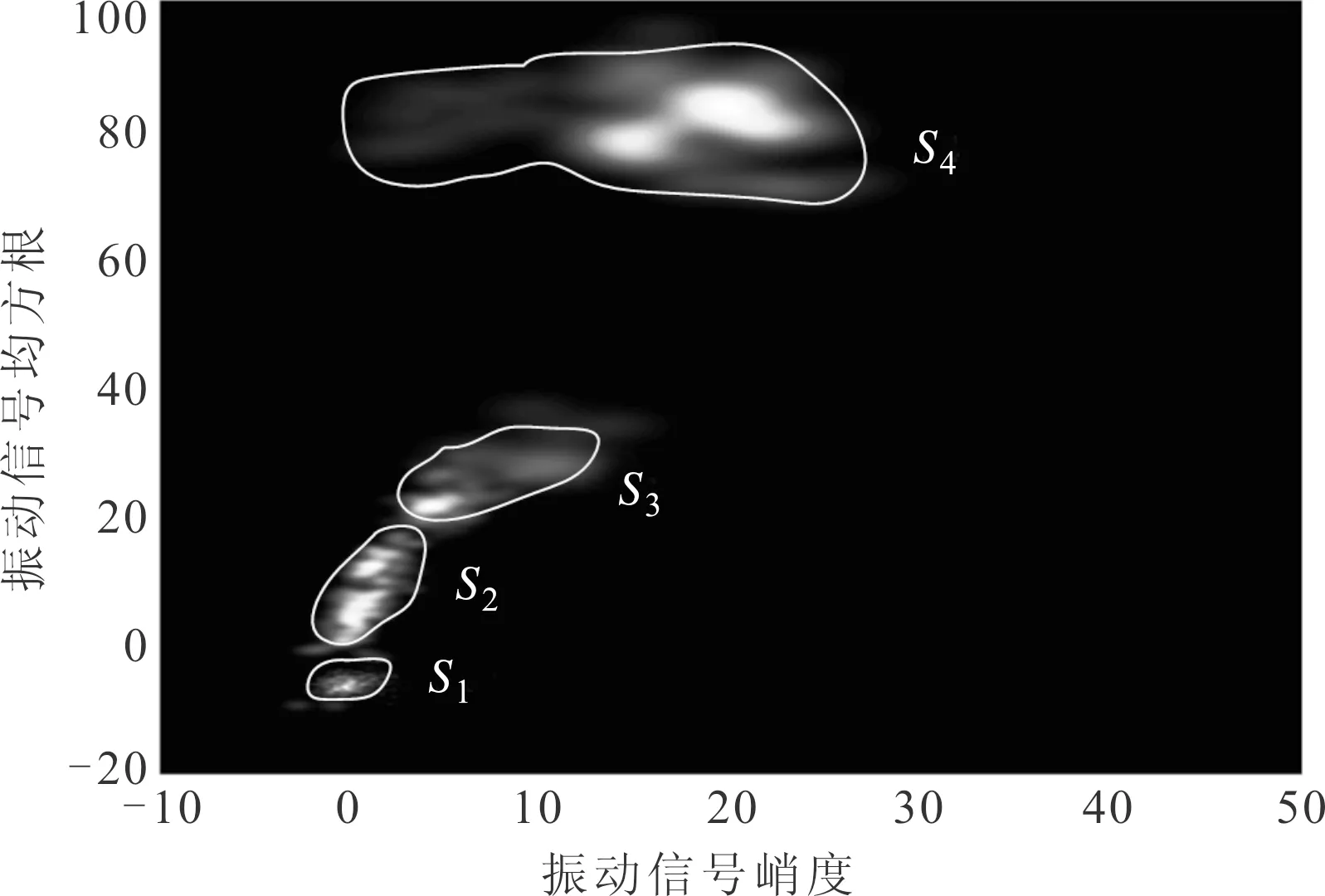
(d)142 h图8 按类概率图像模型更新过程

(2)动态按类概率图像模型。鉴于现有方法无法实时可视化显示的问题,本文提出了按类可视化概率图像模型,可实时更新设备运行时的可视化状态。选择二维性能指标序列的前100个样本点建立初始按类概率模型,其更新过程见图8。在刚开始运行阶段,滚动轴承处于正常状态,性能指标数据变化较小,这些样本点属于正常类,按类图像模型中只有这一类,如图8a所示。随着运行时间的增加,滚动轴承性能发生退化,性能指标数据变化率增大,按类图像模型中的类型越来越多,如图8b中有2类、图8c中有3类、图8d中有4类。因此,该图像模型既融合了均方根指标和峭度指标,又能准确直观地显示滚动轴承的退化过程,进而准确地评估可靠性的下降程度。

3.3 滚动轴承实时可靠性评估

按类概率图像模型中,根据非正常类的图像面积占总图像面积的比值得到故障率。以图8d为例,每一类的区域面积即为白色分类边界线包含的部分,其中正常类面积为S1,所以该图中故障率为(S2+S3+S4)/(S1+S2+S3+S4),再通过式(11)可得到可靠性指标。

图9为根据不同的按类概率图像模型得到的滚动轴承实时可靠性指标曲线,可以看到:

(1)滚动轴承运行早期状态平稳,特征指标分布的区域相对稳定,可靠性指标为1;

(2)当运行时间达到89 h,可靠性指标开始下降,且随着运行时间的增加,轴承不断劣化,可靠性指标越来越小;

(3)当运行时间大约在115 h左右,可靠性指标几乎为0,表明在115 h后滚动轴承处于故障后期阶段。

图9 滚动轴承实时可靠性指标曲线

为了验证本文模型是否能够及时跟踪滚动轴承的退化过程,以及可靠性指标是否能够实时反映滚动轴承的退化程度,对89 h和115 h的振动数据进行包络谱分析,并采用最小熵解卷积(MED)对原始数据进行降噪处理[16],结果如图10、图11所示。

从图10、图11中可以看出,故障特征频率为230.5 Hz,非常接近实验轴承的外圈故障特征频率236.4 Hz。故障特征频率的幅值随着滚动轴承的退化逐渐增大,与实际结果吻合,表明本文模型能够及时跟踪滚动轴承的退化过程,得出的可靠性指标能够实时反映滚动轴承的退化程度。

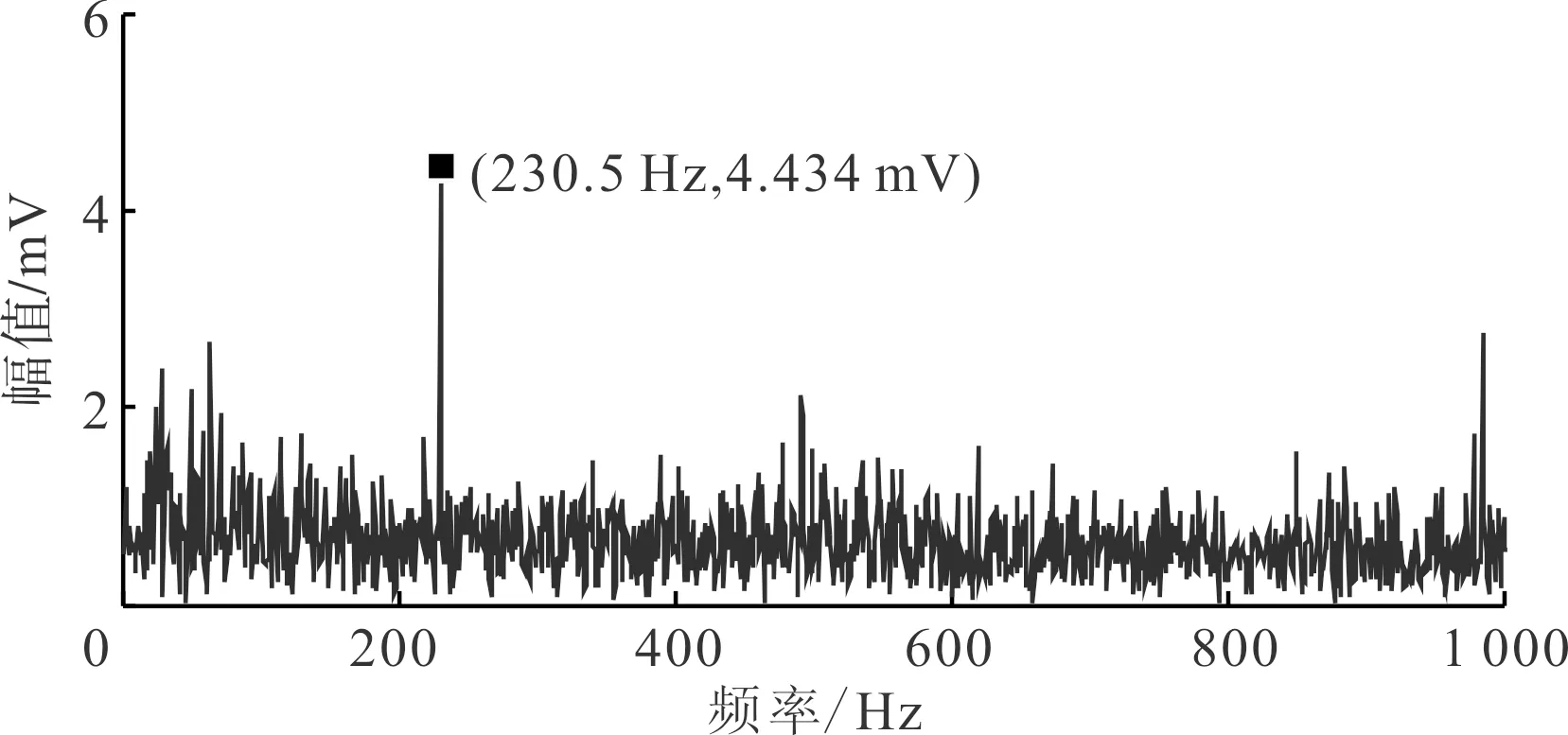
图10 89 h振动信号的包络分析结果

图11 115 h振动信号的包络分析结果

4 结 论

针对目前滚动轴承性能指标的概率模型大多为单性能指标的静态概率模型,且与实际概率模型误差较大的问题,本文基于核密度法建立了动态按类概率图像模型,并将该概率模型中各点的概率转化为彩色值,得到一个能够直观显示滚动轴承退化状态的按类概率图像模型。通过拉依达准则确定分类边界线,并在按类概率图像模型中计算非正常类的图像面积占总图像面积的比值,得到可靠性指标。通过分析样本的不断积累扩充进行模型的更新,实现了不同时刻滚动轴承可靠性的评估。实验结果表明,基于按类统计的滚动轴承可视化可靠性动态评估技术,可以实时准确评估滚动轴承的运行性能可靠性。

参考文献:

[1] 屈梁生,何正嘉. 机械故障诊断学 [M]. 上海: 上海科学技术出版社,1986: 4-11.

[2] 黄文虎,夏松波,刘瑞岩,等. 设备故障诊断原理、技术及应用 [M]. 北京: 科学出版社,1996: 9-15.

[3] 徐敏,黄邵毅. 设备故障诊断手册-机械设备状态检测和故障诊断 [M]. 西安: 西安交通大学出版社,1998: 1-5.

[4] 李海波. 智能化轴承故障诊断仪的工程设计与研制 [D]. 沈阳: 沈阳理工大学,2009: 1-3.

[5] LU H,KOLARIK W J,LU S S. Real-time performance reliability prediction [J]. IEEE Transactions on Reliability,2001,50(4): 353-357.

[6] 丁锋,何正嘉,訾艳阳. 基于设备状态振动特征的比例故障率模型可靠性评估 [J]. 机械工程学报,2009,45(12): 89-95.

DING Feng,HE Zhengjia,ZI Yanyang. Reliability assessment based on equipment condition vibration feature using proportional hazards model [J]. Journal of Mechanical Engineering,2009,45(12): 89-95.

[7] NELSON W. Analysis of performance degradation data from accelerated tests [J]. IEEE Transactions on Reliability,2006,91: 200-208.

[8] 马家驹,梁文梅. 滚动轴承振动统计特性分析 [J]. 轴承,1994(1): 33-37.

MA Jiaju,LIANG Wenmei. Analysis of vibration statistical characteristics of rolling bearings [J]. Bearing,1994(1): 33-37.

[9] KALLAPPA P,BYINGTON C S,KALGREN P W,et al. High frequency incipient fault detection for engine bearing components [C]//Proceedings of the ASME Turbo Expo. New York,USA: ASME,2005: 413-427.

[10] BYINGTON C S,ORSAGH R,KALLAPPA P,et al. Recent case studies in bearing fault detection and prognosis [C]//IEEE Aerospace Conference Proceedings. Piscataway,NJ,USA: IEEE,2006: 1656077.

[11] 徐东,徐永成,陈循,等. 基于EMD的灰色模型的疲劳剩余寿命预测方法研究 [J]. 振动工程学报,2011,24(1): 104-110.

XU Dong,XU Yongcheng,CHEN Xun,et al. Residual fatigue life prediction based on grey model and EMD [J]. Journal of Vibration Engineering,2011,24(1): 104-110.

[12] PARZEN E. On estimation of a probability density function and mode [J]. The Annals of Mathematical Statistics,1962,33: 1065-1076.

[13] CAIN J B. An improved probability neural networks and its performance relative to other model [C]//Application of Artificial Neural Networks. Orlando,USA: SPIE Press,1990: 358-359.

[14] FUGATE M L,SOHN H,FARRAR C R. Vibration-based damage detection using statistical process control [J]. Mechanical Systems and Signal Processing,2001,15(4): 707-721.

[15] 符祥,郭宝龙. 图像插值技术综述 [J]. 计算机工程与设计,2009(1): 141-144.

FU Xiang,GUO Baolong. Overview of image interpolation technology [J]. Computer Engineering and Design,2009(1): 141-144.

[16] SAWALHI N,RANDALL R B,ENDO H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis [J]. Mechanical Systems & Signal Processing,2007,21(6): 2616-2633.

[本刊相关文献链接]

陈保家,汪新波,严文超,等.采用品质因子优化和子带重构的共振稀疏分解滚动轴承故障诊断方法.2018,52(4):70-76.[doi:10.7652/xjtuxb201804010]

夏平,徐华,马再超,等.采用改进HVD与Lempel-Ziv复杂性测度的滚动轴承早期损伤程度评估方法.2017,51(6):8-13.[doi:10.7652/xjtuxb201706002]

张俊红,马梁,鲁鑫,等.机动飞行下挤压油膜阻尼器对碰摩故障转子系统的影响.2015,49(11):62-70.[doi:10.7652/xjtuxb201511011]

李军宁,陈渭,谢友柏.采用知识流理论的高速滚动轴承打滑失效试验台集成设计.2015,49(5):87-93.[doi:10.7652/xjtuxb201505014]

唐贵基,王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用.2015,49(5):73-81.[doi:10.7652/xjtuxb201505012]

易均,刘恒,刘意,等.歪斜安装对组配轴承转子系统动力学特性影响.2014,48(9):107-111.[doi:10.7652/xjtuxb201409 018]

付新哲,张优云,朱永生.滚动轴承故障诊断的案例推理方法.2011,45(11):79-84.[doi:10.7652/xjtuxb201111015]

栗茂林,王孙安,梁霖.利用非线性流形学习的轴承早期故障特征提取方法.2010,44(5):45-49.[doi:10.7652/xjtuxb 201005010]

王晓冬,何正嘉,訾艳阳.滚动轴承故障诊断的多小波谱峭度方法.2010,44(3):77-81.[doi:10.7652/xjtuxb201003016]