采用符号时间序列分析的轴承早期微弱故障预警

韦祥,李本威,张赟

(中国人民解放军海军航空大学航空基础学院,264001,山东烟台)

滚动轴承是旋转机械的重要支撑传动部件,轴承振动状态监控是保证系统稳定运行的重要技术手段。轴承在长时间运转时,其失效过程包含早期磨损、损伤开始、疲劳剥落、严重磨损、轴承失效这几个过程。对轴承的故障诊断方法有小波变换法、包络分析法、声发射法和一些统计量法等,这些方法主要针对轴承明显失效阶段的故障进行特征提取与诊断,当发现明显特征时已经必须停机检修,因此现有的研究方法对早期微弱故障预警和性能衰退监控尚有较大的不足。

从动力学角度考虑,当轴承产生早期磨损时,相比正常状态其外激励、刚度、阻尼等均有一定变化,导致动力学结构发生了变化。符号时间序列分析(symbolic time series analysis,STSA)是非线性动力学结构分析的重要方法之一,在保留动力学结构主要特征的基础上降低动力学噪声和测量噪声的影响,广泛运用于机械故障定位[1]、故障分类[2]、振动信号降噪[3]、早期故障状态突变检测[4]等方向。其核心思想包含两个内容,一是通过粗粒化编码算法将时间序列转换为符号序列,其次通过样本熵、香农熵、Lempel-Ziv复杂度(lempel-ziv complexity,LZC)等参量定量表示符号序列的动力学结构。

粗粒化编码的合理与否是影响STSA精度的重要因素。目前常用的粗粒化编码方法可分为两类:一类为基于幅值域的分割点划分,如等距划分(equidistant segmentation,EDS)[5]、符号聚合近似(symbolic aggregate approximation,SAX)[6]、等概率划分(Equal probability segmentation,EPS)[7],该类方法以信号数值大小作为分类的依据和阈值;另一类为基于时间域的分割点划分,如固定窗[8]、信号方差[9]、分段线性近似[10]等,该类方法以信号在时间上的拓扑结构相似性作为分割阈值。尽管上述划分方法在不同的领域取得较多的成果,但这样的分割方法存在一定的弊端:①工程应用中若研究的对象是高维系统,相轨迹在高维相空间中具有更加复杂而精细的演化过程,实测一维时间序列难以全面反映系统真实的动力学信息,此外基于振幅域和时域的粗粒化方法都是针对一维时间序列的分割,忽略了相轨迹的空间几何属性,损失了动力学结构的重要信息,对动力学结构表征不够精确;②基于时域分割的阈值选取需要有一定先验知识,划分不当容易导致信号动力学结构表征的失真,具体应用中难以获得有效的先验信息,限制其工程应用。

为了更合理地对时间序列进行划分,提高符号时间序列分析方法对动力学结构表征的精度,减少对先验知识的依赖,实现对轴承早期故障的预警,本文先提出了基于聚类分割相空间(phase space reconstruct clustering segmentation,PRCS)的粗粒化编码方法,再通过LZ复杂度对PRCS形成的符号序列进行复杂性度量,提出一种基于符号时间序列分析的轴承早期微弱故障预警方法(PRCS-LZC方法)。以Duffing方程为研究对象,研究了PRCS-LZC方法对于动力学结构表征的特性,并与常规的粗粒化方法进行了对比。通过对实测轴承早期微弱磨损故障和全寿命性能衰退的监控,验证PRCS-LZC方法对机械动力学结构变化表征的敏感性和轴承早期故障预警能力。

1 粗粒化编码原理

对一个未知的动力系统进行连续观测,获取时间序列x={x1,x2,…,xT},x代表动力系统随时间的演化,xt,t∈[1:T]是长度为N的向量,描述在t时刻系统的状态。为获得x的符号时间序列,需对状态空间Ω(Ω⊂R)分割成有限个子集λ1,λ2,…,λs,并满足如下条件[1]

∅,i≠j

(1)

式中:Λ代表整个符号空间;s为状态空间分割的数量。对分割的每个子空间λi赋予唯一的符号,原时间序列x落入该空间的观测值xt被唯一的符号化,由此完成了x由Ω→Λ的转化,该过程被称为粗粒化编码。

2 聚类分割相空间的时间序列粗粒化编码方法

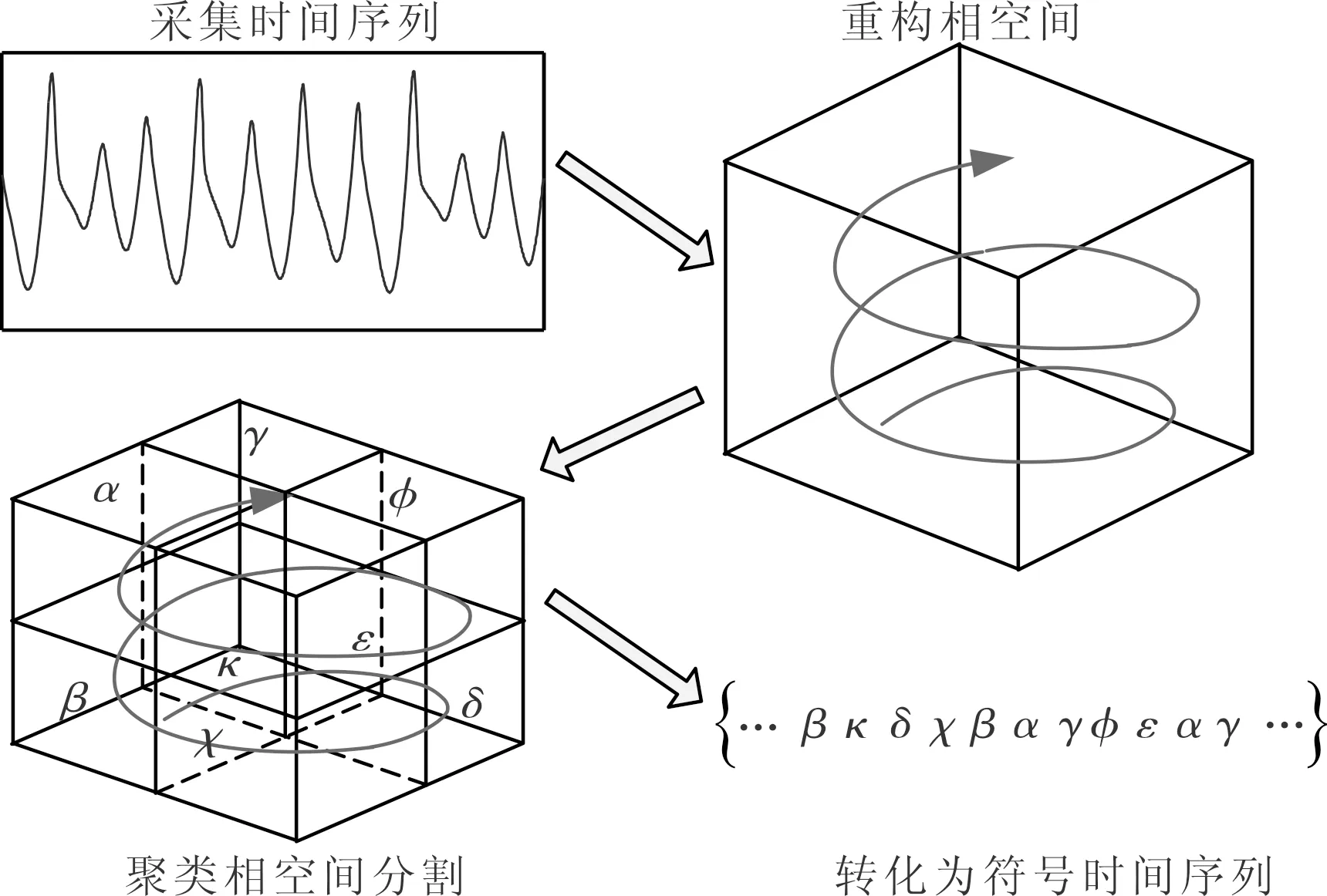
图1 PRCS方法原理示意图

无论是在科学领域还是工程领域,真实动力系统往往是未知的。由于认知或者实验条件的局限,只能通过若干个参量对系统进行描述,并不能完全代表动力系统的全貌,因此从实测时间序列去重构系统的真实动力学行为具有重要意义[11]。直接对重构的相轨迹进行分割可以更真实反映动力系统的结构信息。为此,本文提出了PRCS的粗粒化编码方法,其原理如图1所示。首先对时间序列进行相空间重构,还原系统的真实动力学结构,其次用聚类算法无监督地对相空间进行分割,将落入标记区间的数据标记为唯一的符号,实现时间序列向符号序列的转化。

图1显示的PRCS流程中涉及到两个关键的问题:一是采用什么样的方法对相空间进行准确的重构;二是采用什么样的聚类方法对重构的相空间进行合理地分割,以准确地对重构轨迹进行符号化处理。

2.1 C-C算法重构相空间与参数自动识别

目前,相空间重构最常用的方法是Packard提出的延迟坐标法[12],Takens证明了如果嵌入维数m≥2d+1(d为动力系统的维数)即可满足重构的Rm空间中的轨线与原动力系统微分同胚[13]。在确定嵌入维数m和时延τ之后,可得重构轨迹为

X=[X(1+(m-1)τ),X(2+(m-1)τ),…,X(N)]=

(2)

为了验证C-C算法和参数自动识别的有效性,对Duffing、Lorenz和Rossler系统进行相空间重构。

Duffing动力学方程如下

(3)

式中:k=0.1;B=11;初值(0,0,0)。

Lorzen系统动力学方程如下

(4)

式中:σ=16;R=45.92;b=4,初值(1,1,1)。

Rossler系统动力学方程如下

(5)

式中:d=0.15;e=0.2;f=10;初值(1,1,1)。

GP算法通过相空间重构计算系统的关联维数,因此本文通过GP算法计算关联维数并与关联维数的理论值进行对比,从而验证相空间重构参数选取的有效性,结果见表1。由表1可知,通过GP算法对典型混沌系统计算的关联维数与理论值极为接近,从而也证明了相空间重构参数选择的合理性。

2.2 k-均值聚类算法分割相空间

聚类算法是依据某种标准无监督地将对象自动分为不同的类别,每个类别中的对象彼此之间有相类似的属性或有近似关系。聚类的数学描述如下:令U={p1,p2,…,pn}表示一个模式集合,pi表示第i个模式,i={1,2,…,n};若Ct⊆U,t=1,2,…,k表示对U聚类的结果,k为聚类的类别数,则需满足如下条件

(6)

显然,式(6)与式(1)的数学表达形式完全相同,因此通过聚类对重构的相空间进行分割满足粗粒化编码的基本定义。为了具象地说明基于聚类的相空间分割的思想,采用k-均值聚类算法对式(5)中的三维Rossler混沌吸引子进行分割,结果见图2。由图2可知,k-均值算法按照距离的定义通过三维曲面将Rossler混沌吸引子分割为6类,每一类数据由不同灰度表示,满足式(6)的定义。

表1 典型混沌系统相空间重构与关联维数

图2 Rossler吸引子聚类分割

经k-均值算法分割之后,对每个落入分割区间的数据标记为唯一的符号,图2中由A、B、C、D、E、F表示。由此,Rossler系统的吸引子可以被表示为CDEFABCDEFBCDEFABCDEF…,显然符号A在BCDEF每出现两个周期才出现一次,结合图2分析,吸引子在X-Y平面经历两个周期后会向Z方向跃迁一次,符号序列可被简写为(ABCDEFBCDEF)∞。上述的符号表示体现了Rossler吸引子的周期性质和空间几何性质,说明PRCS能较好地保留系统的内在动力学结构特征。同时,由式(2)可知,相空间矩阵第一行为缺省了(m-1)τ个数据点的原始时间序列,对吸引子分割标记的同时也是对原始时间序列进行相同的标记。

k-均值算法在聚类初始会随机选定数据点作为初始聚类中心,导致聚类结果不稳定。文献[16]利用平均差异度优选初始聚类中心,解决了上述问题。因此本文采用文献[16]的方法确定初始聚类中心,再通过k-均值对相空间进行分割。为了验证k-均值聚类算法编码的稳定性,对式(4)的Lorzen系统和式(5)的Rossler系统进行编码,并采用香农熵和LZ复杂度进行度量,运算次数为20次和50次,结果见表2。

由表2可知,无论随机运算多少次,只要确定初始聚类中心,k-均值算法的计算结果将保持不变,聚类结果稳定。

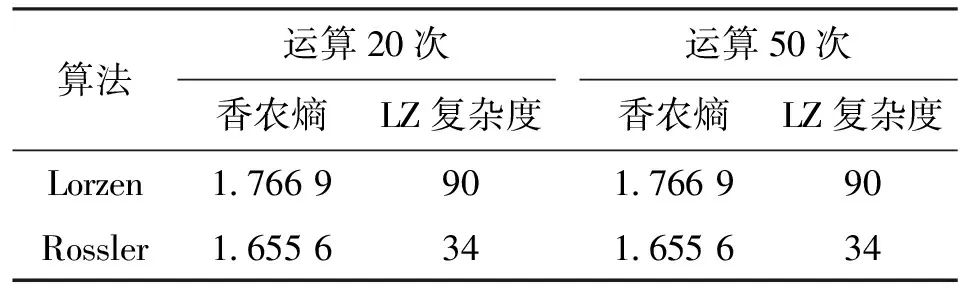
表2 k-均值算法分割相空间稳定性验证

3 PRCS-LZC方法性能分析

3.1 动力学结构表征能力验证

符号时间序列分析的目的是用符号序列对动力学结构进行定量表征。为了验证本文PRCS算法对时间序列分割的有效性,本文以Duffing系统为研究对象,通过PRCS算法对不同策动力下Duffing响应时间序列进行粗粒化处理,再通过LZC对符号序列进行度量。将度量结果与关联维数进行对比,验证PRCS-LZC法对动力学结构表征的有效性。本文方程中的变量和参数均进行了无量纲化处理。

受迫Duffing系统动力学方程如下

(7)

(a)f取值区间为[0.21,0.40]

(b)f取值区间为[0.41,0.60]

(c)f取值区间为[0.61,0.80]图3 Duffing方程在不同载荷激励下的相轨线

由图3可知,在不同载荷激励下,Duffing振子出现同宿轨道周期态、分叉、混沌和大尺度周期态等丰富的动力学行为。f取值为0.21、0.24、0.25、0.36、0.37、0.51、0.61、0.65、[0.75,0.80]等情况下系统处于周期态,系统复杂性较低。f取值为0.30、[0.39,0.50]、[0.55,0.60]、[0.62,0.64]、[0.66,0.68]、[0.70,0.72]等处于混沌态,复杂度较高。

采用PRCS-LZC方法(聚类类别数k=30)和关联维数法(重构维数m=8,时延τ=16)对图3中不同f取值条件下的动力学结构进行度量,结果见图4,幅值均经过归一化处理,归一化公式如下

(8)

式中:X为归一化至[0,1]的幅值;x为原始时间序列;xmin为原始时间序列的极小值;xmax为原始时间序列的极大值。

图4中PRCP-LZC方法和关联维数方法均保持了高度相似的变化规律,同时对周期态和混沌态进行了明显的区分。系统处于周期态时,两种方法所得数值均较低;系统处于混沌态时,两种方法所得数值均较高。曲线变化规律与图3中相轨迹复杂程度变化保持一致,两条曲线的相关性系数为95.85%,从而验证了PRCS-LZC方法对动力学结构表征的有效性,也说明该方法是一种有效的粗粒化方法,较好的保留了系统的动力学结构。

符号时间序列分析的一个重要特点是具有优良的抗噪能力,因此对式(7)在不同f激励条件下求解的响应添加信噪比为10～80 dB的高斯白噪声,通过PRCS-LZC方法对添加噪声后的响应进行度量。计算不同信噪比条件下PRCS-LZC方法与图4中的关联维数曲线的相关系数和均方根误差,作为动力学结构度量准确性的参数,结果见图5。

图5 不同信噪比下PRCS-LZC方法的度量精度与误差曲线

由图5可知,PRCS-LZC方法的度量精度随信噪比的增大而增大。由相关系数和均方根误差变化趋势分析可知,当信噪比大于等于40 dB时,噪声对于PRCS-LZC方法的度量能力几乎无影响,从而验证了PRCS-LZC方法有较好的抗噪能力。

3.2 PRCS-LZC方法与常规算法精度对比

选取EDS、EPS、SAX粗粒化方法与PRCS进行对比,通过LZ复杂度对符号序列进行度量,验证不同粗粒化方法产生的符号序列对动力学结构度量精度的差异。同样,以式(7)的Duffing系统为验证对象,以关联维数作为基准进行对比验证。

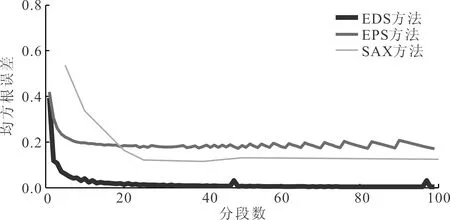
图6 符号序列重构的原信号均方根误差曲线

分数段是影响STSA精度的重要因素,因此需选择合理的分段参数进行对比。构造一个高斯小波函数,选取分段数为2～100进行粗粒化编码(由于SAX方法的限制,分段数选取5、10、20、25、40、50、100,符号数为10),通过EDS、EPS、SAX方法产生的符号序列对原信号进行重构,并计算符号序列与原信号的均方根误差,作为重构信号与原信号的信息损失量的度量,结果见图6。由图6可知,重构信号与原信号的均方根误差随分段数增加而减小,分段数为30时误差基本保持不变,说明分段数大于30时符号序列已经保留信号的大部分信息,重构作用减弱。值得注意的是,图6中不同方法均方根误差在数值上的差异主要由算法原理导致,并不代表粗粒化编码算法的优劣。

根据上述分析,选取10、20、30、40、50分段条件进行对比,结果见图7。

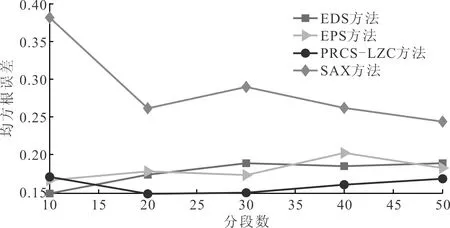
图7 不同粗粒化方法的动力学结构表征精度的均方根误差曲线

由图7分析可知,PRCS-LZC方法在分段数为10时对Duffing系统度量能力较EDS、EPS方法效果差,N≥20时PRCS效果优于EDS、EPS和SAX方法。在分段数为20和30时,PRCS-LZC方法对系统有较准确地表征,计算效率也较高。

4 PRCS-LZC方法在轴承状态监控中的应用

轴承产生早期微弱磨损时,其振动幅值和正常状态相比无显著变化,磨损的微小金属颗粒也难以有效监控,常规手段很难进行早期预警。然而,轴承在产生早期磨损时,其内在动力学结构产生了变化。由图4可知,PRCS-LZC方法表现出了对于Dufifng方程动力学结构变化的敏感性和对周期稳定运动与混沌运动的良好区分能力。利用这种特性,以PRCS-LZC方法作为运动稳定性的特征参量,对旋转机械进行早期微弱故障监测和全寿命性能衰退规律进行研究。采用PRCS-LZC方法对机械系统状态监控原理见图8。

图8 PRCS-LZC方法机械状态监控原理

图9 IMS全寿命轴承试验原理图

美国智能维护系统中心(IMS)对轴承进行了全寿命疲劳试验[17],试验原理见图9。

对轴承加载2 721.554 kg的径向载荷,转速保持2 000 r/min,采样频率为20 kHz,每10 min进行一次采集,采样时间1 s,每次采集形成一个数据文件,试验共采集984个文件数据。试验结束后轴承1产生故障。从每个文件中选取3 000点采用PRCS-LZC方法进行计算,聚类数l=20,轴承1的早期故障监测结果如图10所示。

图10 轴承1的早期故障监测结果

由图10可知,采用PRCS-LZC方法在轴承正常运转时数值基本保持不变,在513个文件后数值逐渐增大,说明该时刻轴承内在动力学结构发生了改变,PRCS-LZC法检测到了轴承早期磨损的故障。此时振幅却未明显增加,说明PRCS-LZC法检测优于常规的状态监控方法。PRCS-LZC法的数值在第700个文件产生突变,检测到了故障明显加剧的数据,之后PRCS-LZC进入快速变化期,振幅也明显加大,说明轴承明显进入加速失效阶段。试验结果说明PRCS-LZC方法可以对早期微弱故障和全寿命性能衰退规律进行监控,有良好的工程应用价值。

5 结 论

本文提出了一种轴承早期微弱故障预警方法 ——PRCS-LZC方法。相比常规的EDS、EPS、SAX等一维时间序列分割方法,PRCS-LZC方法能更好地保留动力学结构的内在特征,对空间相轨迹进行分割的粗粒化思想更符合动力学结构特征提取的机理,具有更加准确的几何意义,而且对动力学结构表征精度也更高。同时,该方法只有聚类类别数一个可调参数,具有依赖参数少的优点。经研究,类别数为20和30在动力学表征精度和计算效率之间有较好的平衡。利用本文方法对动力学结构表征的精确性和对动力学结构变化的敏感性,实现了轴承早期微弱故障预警和全寿命性能衰退监测。

参考文献:

[1] ALAMDARI M M,SAMALI B,LI J C. Damage localization based on symbolic time series analysis [J]. Structural Control and Health Monitoring,2015,22(2): 374-393.

[2] 张华,曾文韬,鄢威. 基于符号动力学信息熵与SVM的液压泵故障诊断 [J]. 振动测试与诊断,2017,37(2): 288-293.

ZHANG Hua,ZENG Wentao,YAN Wei. Fault diagnosis of hydraulic pump based on symbolic dynamic entropy and SVM [J]. Journal of Vibration,Measurement and Diagnosis,2017,37(2): 288-293.

[3] SARKAR S,MUKHERJEE K,JIN Xin,et al. Optimization of symbolic feature extraction for pattern classification [J]. Signal Processing,2012,92(3): 625-635.

[4] GUPTA S,RAY A,KELLER E. Symbolic time series analysis of ultrasonic data for early detection of fatigue damage [J]. Mechanical Systems and Signal Processing,2007,21(2): 866-884.

[5] PARK J Y,KWON D. Detection of failure precursors in multilayer ceramic capacitors based on symbolic time series analysis [J]. Nanoscience and Nanotechnology Letters,2016,8(1): 75-80.

[6] ANITA S A,NICHOLAS W. Symbolization of time-series: an evaluation of SAX,persist,and ACA [C]// 2011 4th International Congress on Image and Signal Processing. Piscataway,NJ,USA: IEEE,2011: 2223-2228.

[7] HOU Fengzhen,HUANG Xialin,CHEN Ying. Combination of equiprobable symbolization and time reversal asymmetry for heartbeat interval series analysis [J]. Physical Review: E Statistical,Nonlinear and Soft Matter Physics,2013,87(1): 012908.

[8] GUERRA-FILHO G,ALOIMONOS Y. A language for human action [J]. Computer,2007,40(5): 42-51.

[9] ZINNEN A,LAERHOVEN K V,SCHIELE B. Toward recognition of short and non-repetitive activities from wearable sensors [C]// European Conference on Ambient Intelligence. Berlin Germany: Springer-Verlag,2007: 142-158.

[10] SANT A A,WICKSTRO N. A symbol-based approach to gait analysis from acceleration signals: Identification and detection of gait events and a new measure of gait symmetry [J]. IEEE Transactions on Information Technology in Biomedicine,2010,14(5): 1180 -1187.

[11] 孟庆芳. 非线性动力系统时间序列分析方法及其应用研究 [D]. 济南: 山东大学,2008: 21-22.

[12] PACKARD N H,CRUTCHFIELD J P,FARMERS J D,et al. Geometry from a time series [J]. Phys Rev Lett,1980,45(9): 712-716.

[13] TAKENS F. Reconstruction theory and nonlinear time series analysis [J]. Handbook of Dynamical Systems,2010,3(3): 347-377.

[14] KIM H S,EYKHOLT R,SALAS J D. Nonlinear dynamics,delay times,and embedding windows [J]. Physical: D Nonlinear Phenomena,1999,127(1): 48-60.

[15] 陆振波,蔡志明,姜可宇. 基于改进的C-C方法的相空间重构参数选择 [J]. 系统仿真学报,2007,19(11): 2527-2538.

LU Zhenbo,CAI Zhiming,JIANG Keyu. Determination of embedding parameters for phase space reconstruction based on improved C-C method [J]. Journal of System Simulation,2007,19(11): 2527-2538.

[16] 李武,赵娇燕,严太山. 基于平均差异度优选初始聚类中心的改进k-均值聚类算法 [J]. 控制与决策. 2017,32(4): 759-762.

LI Wu,ZHAO Jiaoyan,YAN Taishan. Improvedk-means clustering algorithm optimizing initial clustering centers based on average different degree [J]. Control and Dicesion,2017,32(4): 759-762.

[17] QIU H,LEE J,LIN J,et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics [J]. Journal of Sound and Vibration,2006,289(4/5): 1066-1090.