解一元一次不等式（组）的高频错误分析及应对策略

◎吴玲芳

不等式和方程都是刻画现实世界的数学模型.利用不等式解决实际问题的关键是找出不等关系，列出不等式.但在解一元一次不等式时，有的同学常因基础不扎实、概念不清、粗心大意、方法未掌握、思维定式等原因，在解题过程中频繁出错.下面就一些典型错误进行分析讲解.

一、常见错误

1.系数化为1时，两边同时乘或除以同一个负数，不等号方向忘记改变.

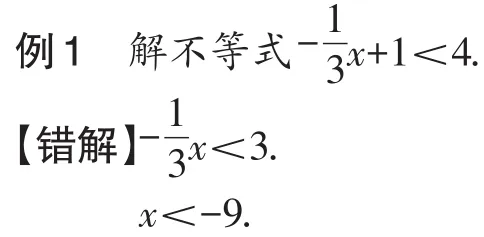
【评析】“不等式的两边都乘（或除以）同一个负数，不等号的方向改变”没有牢固掌握，没有弄清楚等式性质和不等式性质的区别，导致解答出错.正确的解应是x＞-9.

2.分子是多项式，去分母时忽视分数线的括号功能.

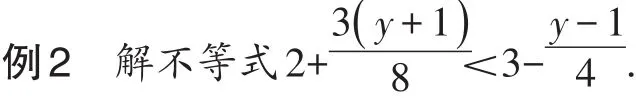
【错解】16+3（y+1）＜24-2y-2.

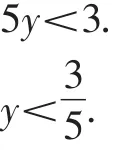
【评析】分数线不仅代表除号，还有括号的功能.去分母时，当分子是多项式时，各分式的分子必须看成一个整体.题中去分母时，没有将分子用括号括起来导致了错误.本题的正确解法应在去分母时将y-1用括号括起来，再去括号，不要跳步骤，正确解为y＜.

3.不等式（组）中含有字母，已知不等式（组）的解集，确定所含字母的取值范围时，错误频出.

例3 若不等式组的解集是x＞3，则m的取值范围是 .

错误一：当两个不等式一样时，不等式的解集是x＞3，所以m=3.

错误二：根据求不等式组解集的口诀“同大取大”可知3比m大，所以m＜3.

【评析】解决本题要借助数轴.依据不等式解集的定义：两个不等式解集的公共部分是不等式组的解集.先将不含字母的不等式的解集x＞3在数轴上表示出来（图1）.

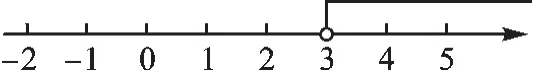
图1

然后由不等式组的解集是x＞3，可知x＞m和x＞3的公共部分是x＞3，所以m在数轴上的位置应该在3的左边（图2）.此时先定下m的大致范围是m＜3.

图2

最后确定临界值.当m=3时，两个解集的公共部分是x＞3（图3），所以临界值能取到，m≤3.

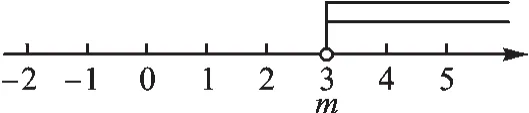
图3

【解题策略】先根据已知信息在数轴上画出不含字母的不等式的解集，然后根据解或解集的情况，画出含字母的不等式的解集，确定字母的大致范围，最后讨论临界值能否取到.

4.思维定式造成设未知数出错.

例4 在“人与自然”的知识竞赛中共有20道题，对于每一道题，答对了得10分，答错了或不答扣5分，至少要答对几道题，其得分不少于80分？

【错解】设至少要答对x道题，由题意得：

10x-5（20-x）≥80.

解得x≥12.

答：至少要答对12道题.

【评析】在列不等式解应用题中，同学们设未知数时，往往受列方程解决问题的迁移，沿用求什么设什么的做法，是错误的.正确的解法是“设答对x道题”.

二、高频错误的应对策略

1.记住表示不等关系的常用关键词.

表示不等关系的常用词语，有“大于、小于、不大于、不小于、超过、不超过、最”等.有些题目中无明显表示不等关系的关键词，例如“打破记录”“更划算”等也都是表示不等关系的词语，根据问题的实际情况理解.

2.区别方程的解与不等式的解、不等式的解集、不等式组的解集.

（1）一元一次方程通常只有唯一解，不等式若有解，一般它的解有无数个.不等式的解集中包含不等式的所有解.

（2）不等式组的解集是不等式组中所有不等式的解集的公共部分.

3.区别等式和不等式的基本性质的不同之处.

等式和不等式的性质大部分都相同，只有一条不同：不等式的两边同乘（或除以）同一个负数，不等号的方向改变.这是不等式特有的性质.

4.注意解不等式中容易出错的环节.

解一元一次不等式的一般步骤与解一元一次方程相同：（1）去分母；（2）去括号；（3）移项；（4）合并同类项；（5）系数化为1.容易出错的环节是去分母和系数化为1.关注易错处，放慢解答速度，则能降低犯错的几率.

5.确定字母的范围应借助数轴.

根据已知解或解集的情况，确定不等式或不等式组中字母的范围时，要充分利用数轴，数形结合，才能更好地解决，先确定大致范围，再确定临界值.

6.关注用不等式解决问题与用方程解决问题的区别和联系.

同学们要注意用不等式和方程解决问题的不同之处：设未知数的方式不同，以及找不等关系时，有些不等关系比较隐蔽，需要根据我们的生活经验加以确定.这就要求大家注重拓宽视野，增加生活经验.