细说数学中的方程思想
2018-06-21白广明
白广明
从问题的数量关系入手,运用数学语言将问题中的条件转化为数学模型(方程、不等式或方程与不等式的组合),将问题中的已知量和未知量之间的数量关系通过适当设元建立起方程(组),然后通过解方程(组)或不等式(组)来使问题获解的思维方式是方程思想.
一、函数中的方程思想
方程与函数本身就有必然的联系,通过建立相等关系,求出未知数的值,因此解决函数问题的关键就是找出相等关系,建立变量之间的等量关系.此类问题常见的形式和解题方法有:用待定系数法列出关于函数解析中待定系数的方程(组),通过解方程(组)求出待定系数的值;将函数图像及坐标轴交点坐标与方程的根对应起来;利用一元二次方程根与系数关系解题.
例1 (2017·安顺)如图1,直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出符合条件的点M的坐标;若不存在,请说明理由.
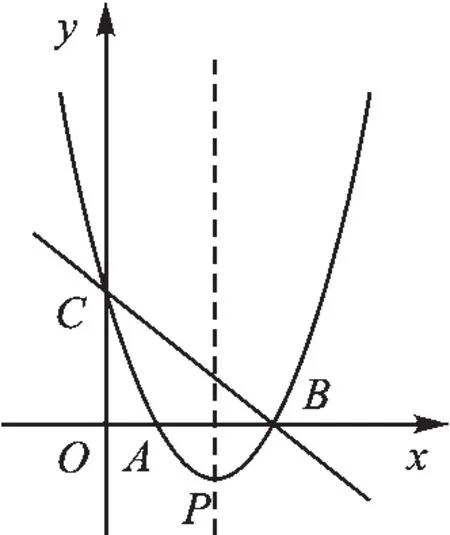
图1
【分析】(1)由直线解析式可求得B、C坐标,利用待定系数法可求得抛物线解析式;(2)由抛物线解析式可求得P点坐标以及对称轴方程,再分MC=MP、MC=PC和MP=PC三种情况,便可得到关于M点坐标的方程,从而求得M点的坐标.
解:(1)∵直线y=-x+3与x轴、y轴分别交于点B、C,
∴B(3,0),C(0,3),
∵抛物线y=x2+bx+c过B、C两点,
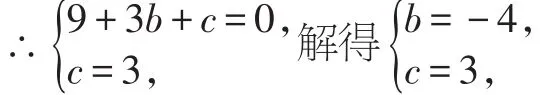
∴抛物线解析式为y=x2-4x+3.
(2)∵y=x2-4x+3=(x-2)2-1,
∴抛物线对称轴为x=2,P(2,-1),设M(2,t),且C(0,3),
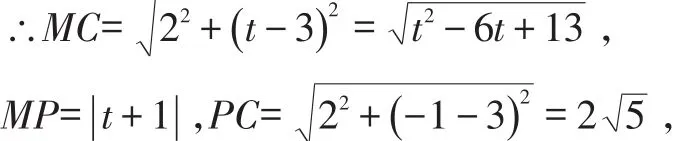
∵△CPM为等腰三角形,

③当PC=PM时,则有 | t+1|=2,解得t=-1+25或t=-1-25,此时M(2,-1+2)或M(2,-1-25).
综上所述,存在满足条件的点M,其坐标为:(2,)或(2,7)或(2,-1+25)或(2,-1-25).
【点评】本题是函数与方程相结合的综合题,找出等量关系、构建方程是解决这类问题的关键,同时,又考查了分类讨论思想.
二、解直角三角形中的方程思想
解直角三角形充分体现了数形结合思想,方程思想体现在:利用勾股定理建立方程,利用三角函数建立等量关系,利用图形的性质建立等量关系.
例2 (2017·宿迁)如图2所示,飞机在一定高度上沿水平直线飞行,先在点A处测得正前方小岛C的俯角为30°,面向小岛方向继续飞行10km到达B处,发现小岛在其正后方,此时测得小岛的俯角为45°.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
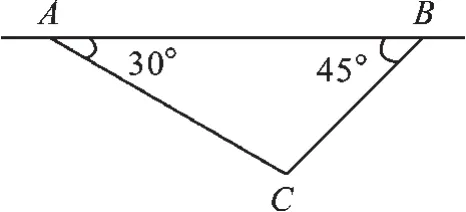
图2
【分析】过点C作CH⊥AB,垂足为H,则CH的长度即为飞机飞行的高度.设CH=xkm,在Rt△ACH中,用x表示出AH的长,在Rt△BCH中,∠BHC=90°,可得BH=CH=x,根据AH+HB=10列出方程,解方程求得x的值,即飞机飞行的高度.
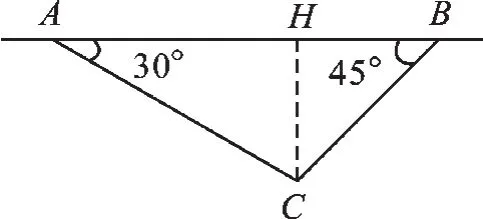
图3
解:如图3,过点C作CH⊥AB,垂足为H,设CH=xkm,在Rt△ACH中,∠AHC=90°,∠CAH=30°,所以AH=3x;在Rt△BCH中,∠BHC=90°,∠CBH=45°,所以BH=CH=x.因为AH+HB=10,所以 3x+x=10,解得x==5-5.
答:飞机飞行高度为(53-5)km.
【点评】构造直角三角形是解直角三角形问题的关键,之后再适当设未知数,建立相等关系列出方程,求出未知数的值即可解答.
三、整式中的方程思想
整式中很多内容与方程有必然的联系,同类项的定义以及整式的化简中就隐含着相等关系,解决这类题的方法:同类项的定义,代数中的恒等变形,利用对比法.
例3 已知A=7x2-mx+n,B=-4y2+2x-1,若A+B中不含有一次项和常数项,求m2-2mn+n2的值.

∴m2-2mn+n2=(m-n)2=1.
例4 单项式3x2y5m+4n与-2xm+2ny4是同类项,求nm的值.

【点评】根据同类项的定义,所含字母相同,相同字母的指数相同,可列出关于m,n的方程组,再求解.
四、几何问题中的方程思想
数与形的结合思想是求解数学问题的重要思想方法,它会使抽象的问题具体化,复杂的问题简单化.与几何图形有关的计算题,若可用方程思想去建立等量关系来解决,会使问题简单化.
1.三角形和四边形与方程思想.
例5 (2016·扬州)如图4,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
【分析】A+B中不含有一次项和常数项,即A+B中一次项系数和常数项都为0,构建方程组求解.
解:A+B=7x2-mx+n+(-4y2+2x-1)
=7x2-4y2+(-m+2)x+n-1,
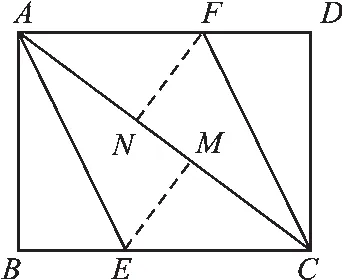
图4
(1)求证:四边形AECF是平行四边形;
(2)若 AB=6,AC=10,求四边形 AECF 的面积.
【分析】(1)先利用“两直线平行,内错角相等”证明∠BAC=∠DCA,根据折叠的性质得出角相等,即∠BAE=∠EAC,∠DCF=∠NCF,进而得出∠EAC=∠FCA,再根据“内错角相等,两直线平行”,得出AE∥CF,从而证明四边形AECF是平行四边形;(2)可以先在Rt△ABC和Rt△CME中利用勾股定理构造方程求得CE的长度,再根据平行四边形的面积公式求得四边形AECF的面积.
证明:(1)∵四边形ABCD是矩形,
∴AB∥CD,∴∠BAC=∠DCA,
由折叠可得∠BAE=∠EAC=∠BAC,
∠DCF=∠NCF=∠DCA,
所以∠EAC=∠FCA,AE//CF,
∴四边形AECF是平行四边形.
(2)因为AB=6,AC=10,△ABC为直角三角形,由勾股定理,得BC=8.设EM=x,那么BE=EM=x,所以CE=BC-BE=8-x,CM=AC-AM=ACAB=10-6=4.
所以x2+42=(8-x)2,解得x=3.
所以S四边形AECF=2S△ACE
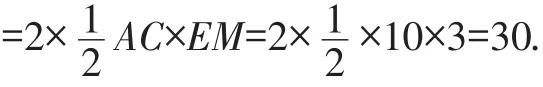
【点评】本题通过设未知数列方程求解,体现了变量间的关系,运用了方程思想.
2.圆与方程思想.
例6 如图5,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O直径BD=6,连接CD、AO.
(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若AO+CD=11,求AB的长.

图5
【分析】(1)连接BC交OA于E点,根据切线长定理和等腰三角形中三线合一定理,可得∠OEB=90°,根据直径对的圆周角为直角可得∠BCD=90°,再根据“同位角相等,两直线平行”即可证明CD∥AO;(2)如图6,根据“两直线平行,同位角相等”,可得∠3=∠4,再证得△BCD∽△ABO,根据相似三角形对应边成比例的性质可得到y与x的关系式,再由题意可得x的取值范围;(3)由(2)中关系式和(3)中的条件可得到关于x和y的方程组,解方程组可得CD,AO的长,再在Rt△AOB中根据勾股定理求得AB的长.
解:(1)连接BC交OA于E点,
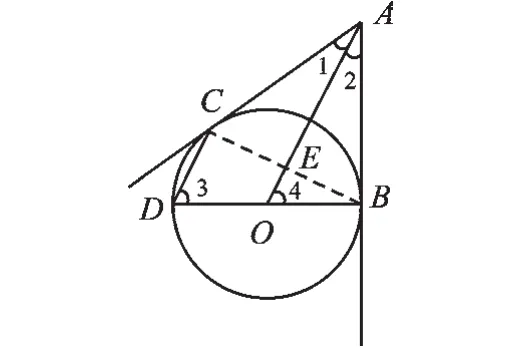
图6
∵AB、AC是⊙O的切线,
∴AB=AC,∠1=∠2,
∴AE是△ABC的中线,
∵O是BD的中点,∴CD∥AO.
(2)∵CD∥AO,∴∠3=∠4,
∵AB是⊙O的切线,DB是直径,∴∠DCB=∠ABO=90°,

【点评】这是一道典型的应用方程求解的几何问题,相等关系是利用了相似三角形的性质和一元二次方程根与系数的关系,体现了数形结合的思想.
