基于小波变换和RBF神经网络的机械故障诊断

路 军

（天津市天特国际贸易有限公司，天津300230）

0 引言

随着自动化程度的提高，大型机械也越来越普遍，当它为我们带来便利的同时，也存在一定的事故隐患。因机械设备故障引起的灾难性事件屡有发生[1]，例如2003年2月美国哥伦比亚载人航天飞机解体事件，造成机上7名人员全部遇难；2000年9月在三峡大坝工地上，一巨型塔带机倒塌，造成3人死亡，30人伤残的重大事故。如果能及时检测故障信号并准确判断故障类型，工作人员就可以及时对故障进行处理，对保护工作人员安全，防止事故进一步恶化具有重要意义。为促进机械故障诊断的研究，美国投入大量的时间和经费对材料在使用过程中发生的变化进行研究，想通过材料状态对故障做出预测[2]，而我国更是将重大设施的运行可靠性、安全性和可维护性的研究作为国家中长期规划中的一部分，充分体现机械故障诊断的重要性[3]。

机械故障诊断是结合信号处理、模型构造和检测预报的综合性学科，早在1960年，就有专家提出这一新兴学科，并总结其具有理论与实际紧密结合的特点，经过半个世纪的发展，机械故障诊断已大量应用于航空、建筑、冶金、能源开采等行业，并涌现了大量优秀诊断方法。机械故障诊断的研究与实现主要从以下四个方向进行：（1）故障信号使用与传感技术，故障诊断是以获取信号为前提的，信号的好坏会对诊断造成直接的影响。在自学习算法出现之前，工作人员主要通过自身经验对故障进行判断，有些经验丰富的专家则将自己总结的规律编写成规律表，供其他工作人员参考，其中以1979年JACKSON[4]根据事故分析经验编写的机械振动分析征兆一般变化规律表最具代表性；传感技术的进步主要依赖传感器检测精度的提高，而在2009年ACHENBACH[5]将传感技术列为重要研究内容之后，传感网络也成为研究热点。（2）故障机理与征兆，“凡事有因才有果”，故障的产生也有一定的原因，这就涉及到机械的原理、结构和适应性等问题，弄清故障产生与表现形式，将有效帮助故障诊断。这方面的研究主要通过构造模型，建立故障特征与机理的联系为目标，经典的模型为2008年BACHSCHMID[6]提出的裂纹转子模型。（3）信号处理与诊断，机械故障诊断往往要求具有实时性，要动态监测机械运行状态。这方面研究开始于2006年，由ANDREW[7]提出，2011 年 MOHAMMAD[8]总结了转子故障中信号处理和监测方法的原理与特征，随后这些研究成果开始应用到机床、车辆、建筑设备等的监测。（4）智能决策与诊断，智能故障诊断拥有过滤和自学习能力，在得到信号后，模拟大脑思维过程，对信号进行处理，过滤正常信号，对异常信号进行分析，通过训练实现对机械的运行状态和故障做出智能的判断和决策。2001年，肖健华[9]将支持矢量理论引入到故障诊断中，给故障诊断提供了一个新的思路，随后出现的基于神经网络的故障诊断模型更是展现出良好的判别性能。

小波变换是一种常用的信号去噪方法，通过选择合理小波基函数和分解层数分离信号的不同状态，然后设定阈值重构信号，以达到区分信号和噪声的目的；在实际应用中，由于BP神经网络收敛速度慢且容易陷入极小值，诊断性能并不理想，而RBF神经网络训练速度快，分类性能良好，在故障诊断中具有很好的实用性。因此，本文将小波变换和RBF神经网络相结合，用于机械故障诊断。

1 算法

1.1 小波变换去噪

机械故障是通过机械内部各种信号进行判别的，这些信号大部分通过传感器采集，所以不可避免会受到机械本身和外界因素干扰，且在信号传输过程中也有可能产生干扰，这些干扰会对故障诊断造成影响，降低诊断准确性，因此，对信号进行去噪处理是很有必要的，目前比较常用的信号去噪方法是傅立叶和小波变换。

傅立叶变换实质是将数据从一个空间变换到另一个空间，它提出“频域”的概念与时域相对应，可通过计算实现信号在时域和频域之间的转换[10]。在时域难以解决的问题可使用傅立叶变换将其引入到频域范围，问题可能会得到很好的解决，对信号的处理通常都是在频域进行的，可用其分析信号在各个频率中的分布状况，方便提取和检测信号重要信息。但是要注意，时域和频域不是同时存在的数据只能在一个域内使用和分析，不能同时使用两个域对同一数据进行处理；同时，傅立叶变换是对信号进行全部变换，不考虑局部细节特征，这会导致信号细节模糊；后来出现了加窗傅立叶变换，通过添加窗口实现保留局部细节特征，但不能根据信号调整窗口大小，仍存在一定的局限性，因为傅立叶变换去噪中存在的问题和故障信号的特点，本文选用小波变换对故障信号进行去噪处理。

小波中的“小”是指它的衰减性，“波”是指它的波动性，小波变换就是利用具有衰减性的波形对数据进行处理。与傅立叶变换相比，小波变换更注重局部细节分析，它通过对信号进行平移及伸缩运算多尺度细化信号，能自适应时频信号分析的要求从而不遗漏信号的任意细节。小波变换广泛应用于以下四个方面[11]：（1）信号与影像压缩，通过小波变换可实现数据压缩，且小波变换具有高压缩比，压缩速度快，压缩损伤小等优点，且在传递中可以抗干扰。（2）信号分析，这是小波变换应用的一大方向，小波变换广泛应用于滤波、边界检测、时频分析、信噪分离、信号识别与诊断等方面。（3）工程技术应用，在机器视觉、图像设计、远端宇宙的研究与生物医学方面等领域都可以看到小波变换的身影。

小波变换具有如下优点：（1）灵活选择小波基针对实际情况选用不同小波基对数据进行分析，以获得最佳的处理效果。（2）去相关性，小波变换对信号具有去相关的作用，而噪声在变换后会有白化的趋势，这也使频域比时域更适合去噪。（3）多分辨率，小波变换使用多分辨率处理信号，可更好的捕捉信号断点、边缘和尖峰位置，保留细节能力更强（4）系数分布稀疏，小波系数没有规律性，使变换后数据熵更低，降低计算量。

小波变换去噪的理论依据主要是：在经过小波变换后，正常信号的能量会集中到少数小波系数上，而噪声不同于正常信号，能量分布在整个小波域中，不会随正交基改变而集中，并且在任何正交基上都会保持相同的幅度。当信噪比变大时，正常信号的小波变换系数会大于噪声的小波变换系数可根据系数数值选择一个合适分割界限，对信号进行处理，以达到去除噪声和保留有用信号的目的目前比较常用的小波去噪方法有阈值法、模极大值法和平移不变法，其中，阈值法具有广泛的适应性且计算速度快，可得到原始信号的最优估计，特别是在信噪比较高的场合，展现出良好的去噪性能，而模极大值法主要应用在信噪比较低的场合，计算速度偏慢，平移不变量法同样存在计算速度慢的缺点，且对信号边缘敏感。经过对常用小波去噪方法的比较，并结合机械故障信号的实际背景，选取典型的小波阈值法对信号进行去噪。小波变换阈值法去噪的基本步骤如下[12]：

（1）分解信号，选择小波基函数并确定分解层数，然后使用Mallat算法对信号进行分解，得到各个尺度上信号的尺度系数和小波系数。

（2）阈值处理，设定分割阈值，认为所有小波系数绝对值小于的信号为噪声，并用0代替噪声对应的小波系数，保留小波系数绝对值超过的信号。

（3）信号重构，根据小波分解的底层低频系数和各层高频系数进行小波重构。

（4）判断信号幅值是否达到要求，如果达到要求，则输出信号，流程结束；否则，将重新分解信号。流程如图1所示。

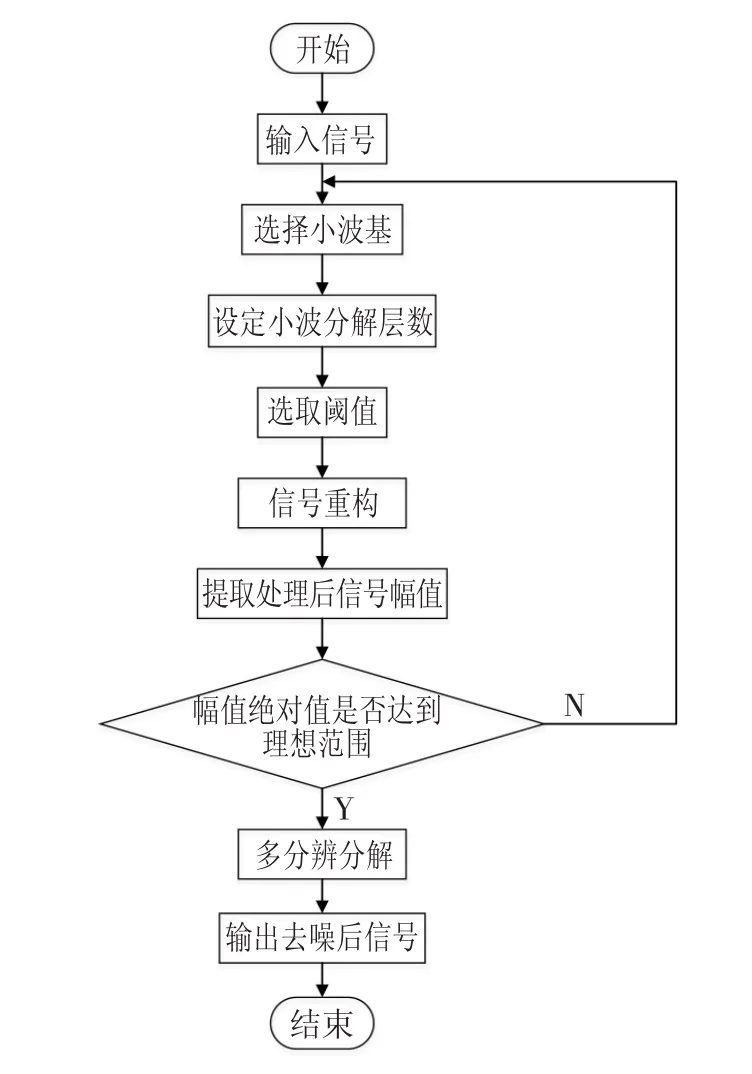
图1 信号去噪流程图

1.2 RBF神经网络

RBF（Radial Basis Function，径向基函数）神经网络来源于生物学，由Moody和Darken[13]提出，致力于模拟人脑思维过程，使机器具有拟人的思维方式，但与BP神经网络不同，它增加了大脑皮层区域中局部调节及交叠的感受野（Receptive Filed）功能，提高网络的判别能力。最常用的RBF神经网络结构如图2所示，在输入与输出层之间，只包含一个隐含层，其中每一层作用各不相同，输入层是网络与外界联系的桥梁，需要处理的数据都是由输入层进入网络的，一般由一些感知单元组成，有些网络输入层还具有归一化数据的功能；隐含层是网络的核心层，用于数据处理与分析，神经网络性能的好坏与隐含层密切相关，本文介绍的RBF神经网络隐含层只有一层，但为了得到更好处理结果，可以设置多层隐含层，例如卷积神经网络的隐含层一般为3~8层，隐含层中包含很多非线性变换，用于输入到隐含空间的转变；输出层主要用于输出处理结果，它是一种线性网络，RBF神经网络中的输出层还具有反馈误差的作用。RBF神经网络常用的径向基函数有以下三种（为基函数宽度）：

（1）高斯函数

（2）反演S型函数

（3）拟多二次函数

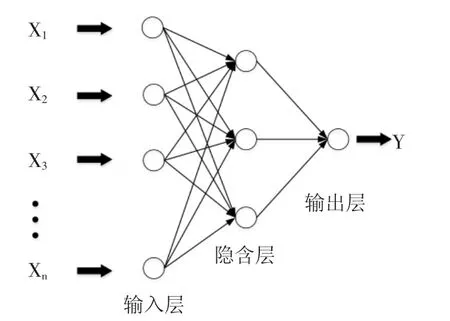
图2 RBF神经网络

在使用RBF神经网络时，要对网络结构和参数进行设计，结构设计主要解决网络隐节点个数及位置问题；参数设计是要确定数据中心、扩展常数和输出节点权值的数值。其中，隐节点的个数决定了数据中心数值，而数据中心数值的选取有随机选取法、自组织选取法、监督选取法三种。

结合故障原因和诊断方法寻找一种可行的技术，对机械故障进行诊断。通常情况下，为实时监测机械运行状态，防止灾难性事故发生，在大型机械的关键位置都安装有传感器。当机械正常运行时各位置传感器采集到的信号会是一个循环且平稳的信号，具有一定的规律性；但是当机械发生故障时，信号往往会发生突变，也就产生了奇异信号，通过准确捕捉并分析这种奇异信号可以判别故障类别。本文采用在线与离线相结合的方式训练RBF神经网络，在训练过程中不断修正网络的数据中心、扩展常数和权值，使其不仅可以自动确定网络结构，而且可以自适应学习样本的分布规律，从而有效提高诊断准确性[14]。

下面给出RBF神经网络和小波变换结合的一个总体概述，先对输入信号进行小波变换处理，降低噪声干扰，再利用小波的多分辨率提取信号特征向量，把特征向量作为RBF神经网络的输入，经过一系列监督学习，得到神经网络的模型，从而达到故障诊断的目的，流程如图3所示。

2 仿真结果

为验证本文提出诊断方法的有效性，采集工厂内机械正常运行和故障信号，并在台式机上完成模型训练和测试。所用台式机配置为Windows 7操作系统，Inter Core i5处理器，2.53GHz主频，4GB 内存，所使用开放软件为MATLAB。实验参数设置如下：从正常信号和故障信号中随机选取75%用于训练，剩下的25%用于测试。

2.1 去噪效果

图4和图5为使用小波变换去噪的现场信号对比，图4中现场信号波动幅度比较大，图5中现场信号细节丰富。在去噪开始前，小波分解层数由经验设定，然后根据处理效果自动调节，使去噪达到更好效果。由图4和图5可知，当现场包含较强噪声时，通过小波变换可滤除大部分噪声，并能很好保留有用信号；同时从图4可以看出，小波变换完成后，信号出现了一定的平移，但并不影响故障判别，不用做特殊处理。

2.2 诊断效果

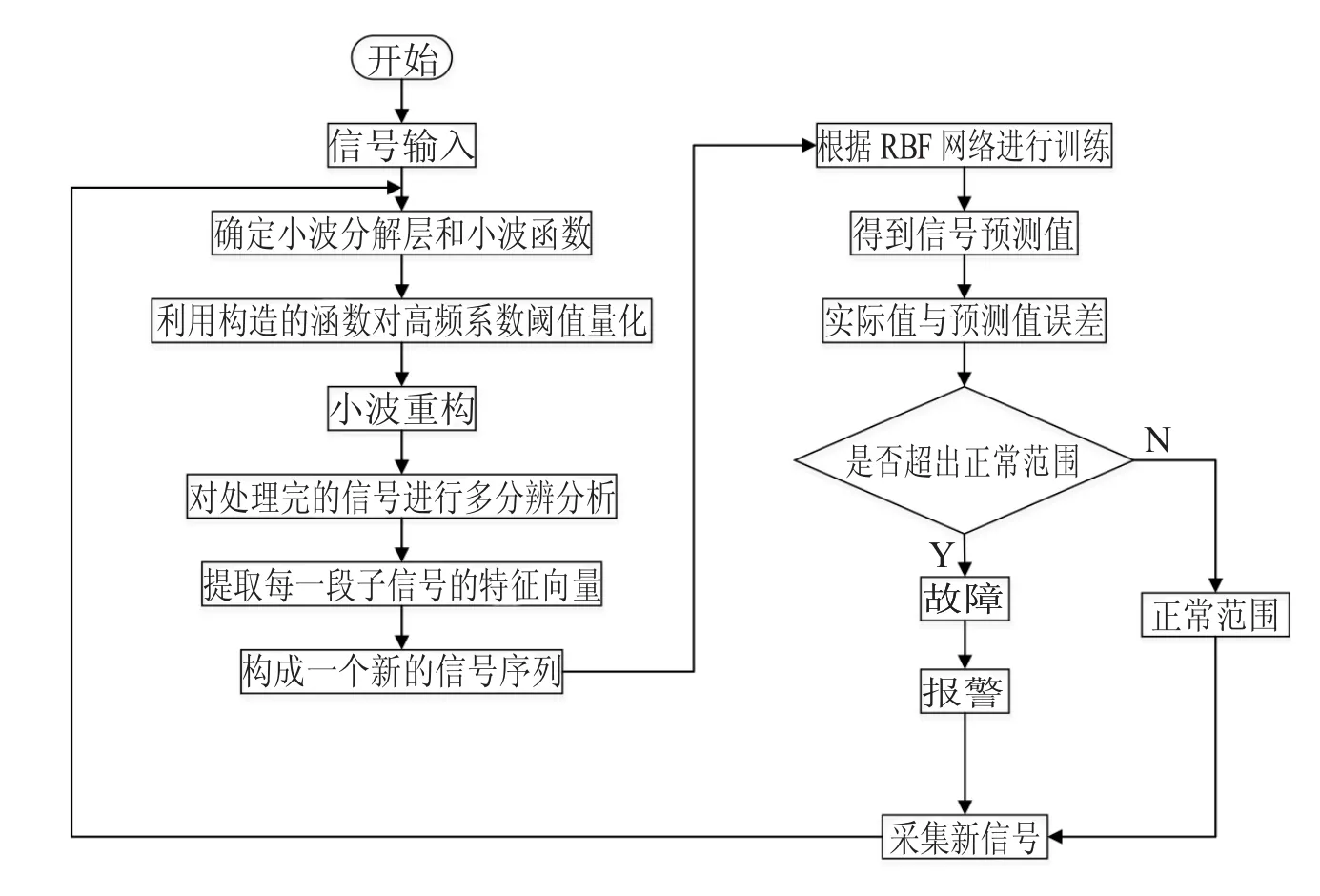
图3 本文算法流程图

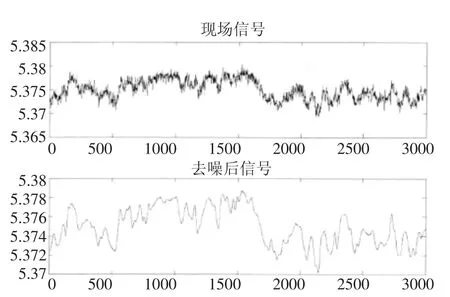
图4 信号去噪

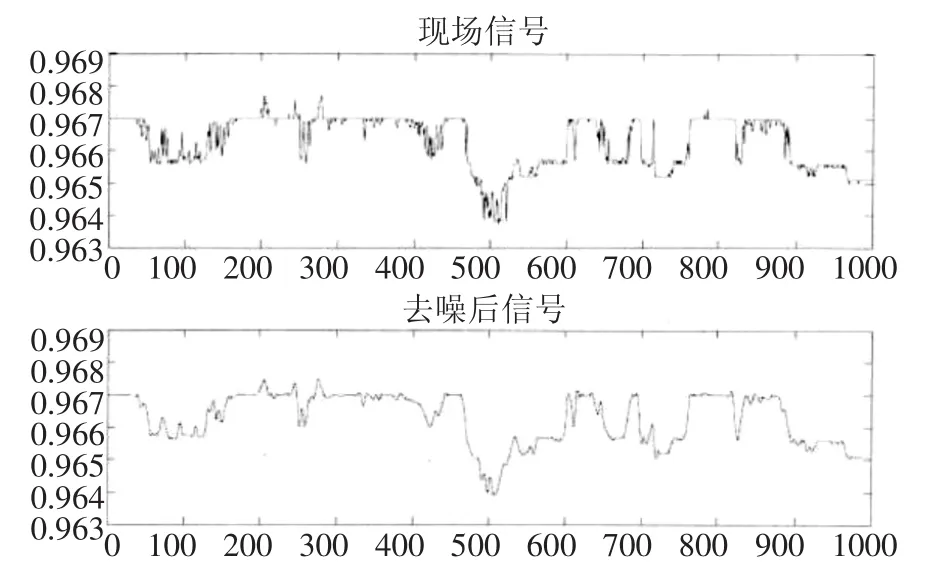
图5 信号去噪

模型训练完成后，使用测试数据进行测试，测试结果为10次测试的平均值如表1所示。由表1可知，噪声会对故障诊断造成一定的影响，使诊断准确性降低，因此，去噪处理是很有必要的；在使用模型方面，不管是对含噪声还是不含噪声的信号，RBF神经网络诊断准确性均高于BP神经网络，充分证明RBF神经网络更适用于机械故障诊断。

表1 诊断结果

3 结论

针对机械故障诊断准确性不高的问题，提出一种基于小波变换和RBF神经网络的机械故障诊断。该方法首先利用小波变换对采集到的信号进行处理，降低机械本身及外界因素带来的噪声干扰；然后使用RBF神经网络代替工作人员对故障进行诊断，排除人为主观因素影响，提高判别准确性。仿真结果表明，本文提出的机械故障诊断方法准确性明显优于人工和BP神经网络，且计算量小，收敛速度快。

[1]钟群鹏，张峥，有移亮.我国安全生产(含安全制造)的科学发展若干问题[J].机械工程学报,2007,43(1):7-18.

[2]涂善东，葛世荣，孟光，等.机械结构强度与失效，机械与制造科学学科发展战略研究报告(2006-2010年)[M].北京：科学出版社,2006.

[3]国家自然科学基金委员会工程与材料科学部.机械工程学科发展战略报告(2011-2020年)[M].北京：科学出版社,2010.

[4]JACKSON C.The practical vibration primer[M].Texas:Gulf publishingCompany,1979.

[5]ACHENBACH J D.Structural health monitoring-What is the prescription[J].Mechanics Research Communications,2009,36:137-142.

[6]BACHSCHMIDN,PENNACCHI P.Crack effects in rotor dynamics[J].Mechanical Systems and Signal Processing,2008,22:761-762.

[7]ANDREWKSJ,DAMINGL,DRAGANB.Areviewon machinerydiagnostics and prognostics implementing condition-based maintenance[J].Mechanical Systems and Signal Processing,2006,20:1483-1510.

[8]MOHAMMAD R M,NORMAN M,MOHAMMAD H M,et al.Rotor fault condition monitoring techniques for squirrel-cage induction machine-A review[J].Mechanical Systems and Signal Processing,2011,25(8):2827-2848.

[9]肖健华，樊可清，吴今培，等.应用于故障诊断的SVM理论研究[J].振动、测试与诊断,2001,21(4):258-262.

[10]袁建虎，何竹青，龙云飞，等.低信噪比信号的连续与离散小波变换比较研究[J].自动化仪表,2009,30(8).

[11]曹毅，张榆锋，毛选珍.小波分析及其信号中的应用[J].现代电子技术,2003,15(12).

[12]李海东，李青.基于阈值法的小波去噪算法研究[J].计算机技术与发展,2009,19(7):56-58.

[13]Moody J,Darken C Learning with Localized Receptive Fields[M],In Proc 1988Connectionist Models Summer School,D Touretzky,G Hinton,and T Sejnowski(Eds.),Carnegie Mellon University Morgan Kaufmann Publishers,1988.

[14]王旭东，绍惠鹤.RBF神经网络理论及其在控制中的应用[J].信息控制,1997,26(4).