类不平衡稀疏重构度量学习软件缺陷预测

史作婷，吴 迪，荆晓远,，吴 飞

(1.南京邮电大学 计算机学院，江苏 南京 210003；2.武汉大学 计算机学院 软件工程国家重点实验室，湖北 武汉 430072；3.南京邮电大学 自动化学院，江苏 南京 210003)

0 引 言

软件缺陷预测是软件工程领域的一个重要研究方向，对于发现程序错误、保障软件质量有重要的意义。已有的软件缺陷预测技术借助于机器学习等方法，通过分析软件代码，提取与软件缺陷相关的度量元，构建模型，找出项目中潜在的缺陷程序模块[1]。

研究表明，软件系统中只有极少数的模块是有缺陷的，这说明数据集的类别分布不平衡。常用的机器学习算法直接用于不平衡数据集分类时会倾向于把有缺陷样本错分到无缺陷类中。但是，将有缺陷样本错误预测与将无缺陷样本错误预测的代价是不同的[2]。为了解决软件缺陷预测中数据不平衡的问题，目前常用的方法是采样法(包括上采样、下采样等)、代价敏感学习方法以及集成学习方法。

现在已经有很多典型的分类方法运用在软件缺陷预测领域中，比如SVM[3]、朴素贝叶斯[4]、决策树[5]、神经网络[6]等算法。最近，一些机器学习领域最新的研究成果，例如字典学习、稀疏表示[7]等也引入到软件缺陷预测中，并且取得了良好的预测效果。代价敏感鉴别字典学习(cost-sensitive discriminative dictionary learning,CDDL)[8]结合稀疏表示字典学习以及代价敏感因子，在提升预测性能的同时也解决了类不平衡问题。代价敏感局部协同表示(cost-sensitive local collaborative representation,CLCR)[9]利用协同表示为给定的一个测试模块找出训练集中的邻居模块，然后使用这些邻居模块的线性组合表示测试模块。

文献[10]提出了基于局部稀疏重构的度量学习方法(local sparse reconstruction based metric learning,LSRML)，首次将距离度量学习方法运用到软件缺陷预测中，在稀疏表示的基础上引入距离度量学习技术。但是该方法并没有针对样本集类别不平衡的问题进行处理，影响了算法性能。因此文中提出一种类不平衡稀疏重构度量学习软件缺陷预测方法(class-imbalance sparse reconstruction metric learning software defect prediction,CSRML)，在学习特征矩阵的阶段融入代价敏感因子，同时加入类别权重提高小类样本距离度量学习的准确性，并在分类预测阶段使用改进加权KNN(improved weighted KNN,IWKNN)算法预测标签。最后在NASA数据集上验证该方法的有效性。

1 相关工作

1.1 代价敏感学习方法

软件缺陷领域中样本错误分类的代价是不同的，通常将无缺陷样本预测为有缺陷样本的情况称为Ⅰ类错分，将有缺陷样本预测为无缺陷样本的情况称为Ⅱ类错分，而Ⅱ类错分的代价远大于Ⅰ类错分。代价敏感学习提高Ⅱ类错分的惩罚，可以生成分类模型来使错误分类的代价最小。例如代价敏感多层感知机(CSMLP)[11]在目标函数中加入一个代价参数来区分不同类错误带来的代价。

1.2 稀疏表示

给定训练样本集X=[X1,X2,…,Xc]∈Rm×n，其中c表示类别数，第i类训练样本集为Xi=[xi,1,xi,2,…,xi,Ni]，Ni表示第i类样本的样本数。对于一个测试样本y，可以看作是训练样本的联合稀疏表示[7]，公式表示为：

(1)

其中，α=[α1,α2,…,αc]T表示稀疏系数向量；μ为使α保持稀疏性的正则化系数。

1.3 基于局部稀疏重构的距离度量学习

(2)

局部权重定义为：

(3)

(4)

其中，r1>r2。

最终得到的稀疏重构项为：

R(xi,A)=(xi-Aβ)TM(xi-Aβ)+σ‖Diβ‖1=

(5)

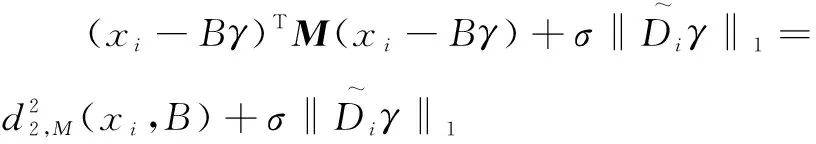
(6)

其中，β表示xi关于样本集A的稀疏表示系数；γ表示xi关于样本集B的稀疏表示系数。

虽然LSRML方法可以学习到鉴别性更好的度量矩阵，但是该方法没有考虑到软件缺陷预测中数据不平衡的问题与代价敏感问题。因此文中在度量矩阵学习阶段引入代价敏感因子来减小样本错分代价，同时更加注重小类样本距离度量学习的准确性，并在测试样本分类阶段使用改进加权KNN算法。

2 类不平衡稀疏重构度量学习软件缺陷预测

文中提出的CSRML方法分为两个阶段：距离度量矩阵学习阶段与使用IWKNN算法分类阶段。第一个阶段可以学习到距离度量矩阵M。在这一阶段中引入代价敏感因子，并为不同类别的样本赋予不同的权重，提高小类样本计算的准确性，目的是使学习到的矩阵能更适用于类别不平衡的数据集。第二个阶段使用IWKNN分类算法进行样本标签预测，使用该算法的目的是在进行分类任务时也考虑样本类别不平衡的问题。

2.1 距离度量矩阵学习

为了解决软件缺陷预测中的数据不平衡问题与样本错分代价不同的问题，在类间稀疏重构项中加入代价敏感因子，得到新的类间稀疏重构项公式：

(7)

其中，cost(i,j)表示样本错分的惩罚值，将有缺陷样本预测为无缺陷样本时惩罚值更大。cost(i,j)的取值为表1中的代价矩阵。

表1 代价矩阵

对于软件缺陷预测来说，少数的存在缺陷的样本需要被检测出来。所以在学习过程中除了增加对错分的惩罚之外，也应该提高小类样本距离度量学习的准确性，可以为不同类别的样本赋予不同的权值，使小类样本之间距离更近。权重计算公式为：

(8)

其中，N表示样本总数；Ni表示第i类样本个数；c表示样本类别数，文中c取值为2。

因此可以得到CSRML算法的目标函数：

(9)

式9可以分成两个子问题来求解：固定M更新β与γ；固定β与γ更新M。目标函数的优化过程就是迭代更新M与β、γ的过程。

2.2 改进加权KNN算法

K近邻算法是一种经典的分类算法，其基本思想是将测试样本标记为其K个近邻样本中类别数最多的那一类[13]。文中在度量矩阵学习阶段没有改变原始样本中数据不平衡分布的情况，因此，在后续的分类任务中还需要考虑不同类别间样本数目差别较大对算法分类性能的影响。

文中引入了IWKNN，为训练样本赋予不同权重，在分类阶段统计测试样本与近邻样本的相似度之和，以此作为样本分类的判决准则。IWKNN算法的步骤如下：

(1)为有缺陷与无缺陷的训练样本赋予不同的权重，使得有缺陷样本具有更大的权重，同一类样本权重相同,如式8所示。

(2)计算测试样本与所有训练样本的马氏距离，公式为：

(10)

(3)找出式10中求出的K个距离测试样本最近的训练样本。

(4)分别计算测试样本与K个近邻样本的相似度，距离越近，相似度越大,计算公式为：

(11)

(5)计算测试样本与K个近邻样本中每类样本的加权相似度之和,计算公式为：

(12)

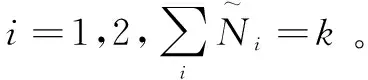
(6)测试样本类别指定为与其加权相似度最大的类，计算公式为：

(13)

结合距离度量矩阵学习阶段以及IWKNN算法分类阶段，可得到CSRML算法的具体步骤：

(1)初始化鉴别矩阵M。初始化矩阵M为欧氏度量矩阵M=I。

(2)更新稀疏系数β与γ。固定矩阵M，依次求得β与γ。

(3)更新半正定矩阵M。固定稀疏系数β与γ，更新矩阵M。

(4)分解半正定矩阵。M=WWT，更新训练样本xi=WTxi。

(5)输出矩阵M。返回步骤2，直到连续两次迭代求得的目标函数值J(M,β,γ)足够接近或者达到最大的迭代次数。

(6)利用IWKNN算法求出测试样本的标签。

3 实 验

3.1 数据库

使用NASA数据库[14-15]中的五个项目作为实验数据，每个项目代表一个NASA的软件系统或子系统，由静态代码度量指标和样本缺陷标签组成。表2列出了数据集的详细信息。从表中可以看出，这五个数据集中有缺陷样本数所占比例都低于13%，有缺陷样本与无缺陷样本这两类样本的数目之间差别较大。

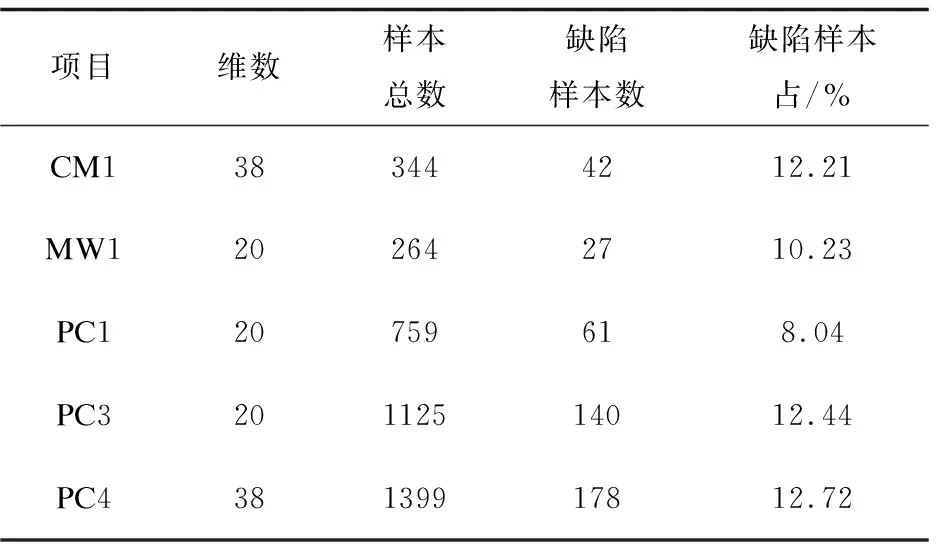
表2 NASA数据集详细信息

3.2 评价指标

采用四个常用的度量指标来评价该算法的实验效果，四个度量指标包括召回率(recall (pd))、假阳率(false positive rate (pf))、F-measure和曲线下面积(area under curve (AUC))。这些度量指标由表3所示的四种预测结果定义。

表3 四种预测结果

其中,pd表示被正确分类的缺陷样本占所有缺陷样本的比例，pf表示被错分的无缺陷样本占所有无缺陷样本的比例。计算公式为：

pd=A/(A+B)

(14)

pf=C/(C+D)

(15)

精准度(precision)用来评价预测模型的准确度，公式为:

precision=A/(A+C)

(16)

F-measure指标用于平衡precision和recall，计算公式为：

(17)

AUC表示ROC曲线下的面积，ROC曲线是由一列pf、pd数据对得到的一条曲线。

3.3 实验结果

CSRML算法主要与软件缺陷预测中的几种典型方法作对比，包括SVM、CC4.5、NB。此外，文中算法是对LSRML算法做的改进，因此也要将其作为对比算法。

CSRML算法与其他方法的对比结果如表4所示。

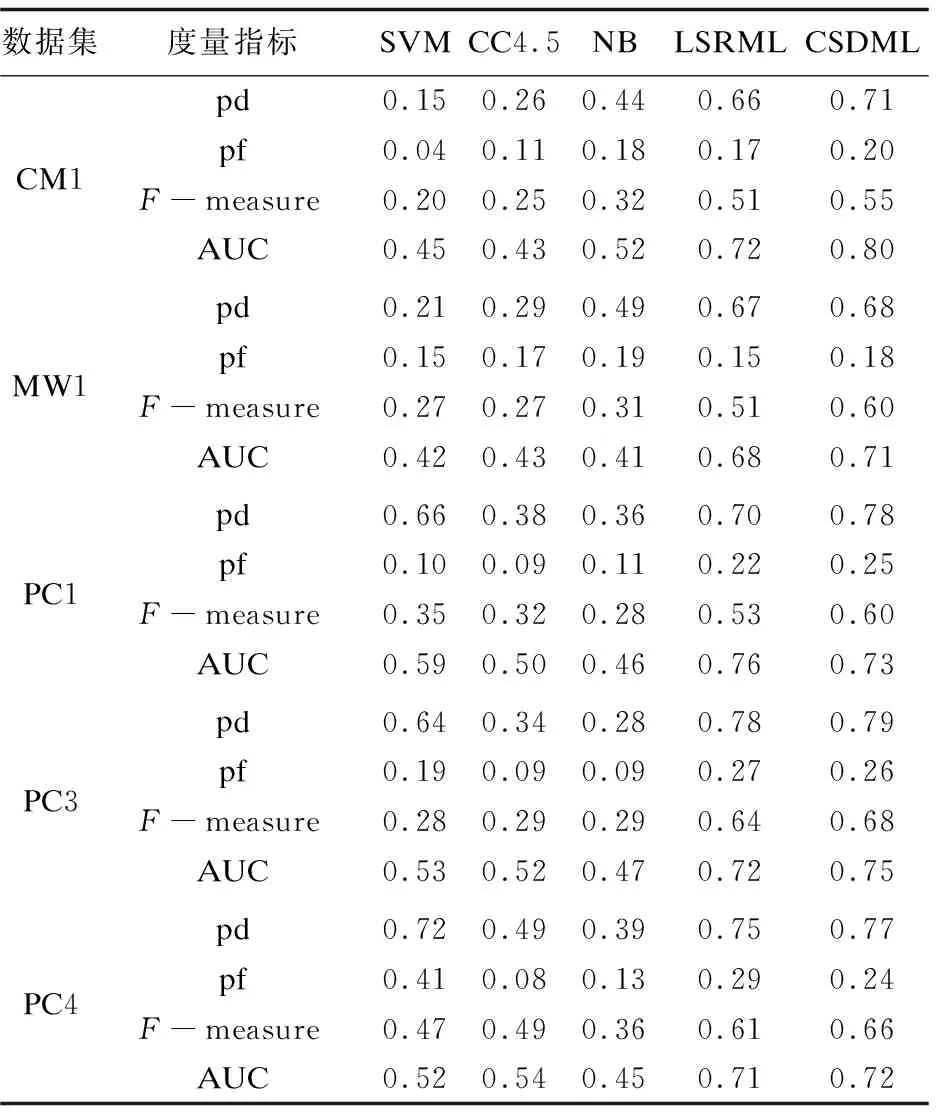
表4 实验结果

从表中可以看出，与传统的算法相比，文中算法有比较明显的优势。而与LSRML算法相比，CSRML方法获得了较高的pd值与F-measure值。通过进一步分析可以得出，CSRML算法的pd平均值比LSRML高0.026，F-measure的平均值比LSRML算法的高0.058。这说明了在度量学习软件缺陷预测中考虑数据集不平衡问题的必要性。

4 结束语

在稀疏重构度量学习的基础上，为度量矩阵学习阶段引入代价敏感因子来减小样本错分代价，同时加入权重来提高小类样本距离度量学习的准确性，并在测试样本分类阶段使用IWKNN算法。在NASA上5个项目的实验结果证明了文中算法的有效性。

参考文献：

[1] 陈 翔,贺 成,王 宇,等.HFS:一种面向软件缺陷预测的混合特征选择方法[J].计算机应用研究,2016,33(6):1758-1761.

[2] 缪林松.基于代价敏感神经网络算法的软件缺陷预测[J].电子科技,2012,25(6):75-78.

[3] ELISH K O,ELISH M O.Predicting defect-prone software modules using support vector machines[J].Journal of Systems & Software,2008,81(5):649-660.

[4] WANG Tao,LI Weihua.Naive Bayes software defect prediction model[C]//International conference on computational intelligence and software engineering.Wuhan,China:IEEE,2010:1-4.

[5] WANG Jun,SHEN Beijun,CHEN Yuting.Compressed C4.5 models for software defect prediction[C]//International conference on quality software. Xi’an, Shaanxi,China:IEEE,2012:13-16.

[6] ZHENG Jun. Cost-sensitive boosting neural networks for software defect prediction[J].Expert Systems with Applications,2010,37(6):4537-4543.

[7] WRIGHT J, YANG A Y, GANESH A, et al.Robust face recognition via sparse representation[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2008,31(2):210-227.

[8] JING Xiaoyuan,YING Shi,ZHANG Zhiwu,et al.Dictionary learning based software defect prediction[C]//International conference on software engineering.[s.l.]:IEEE,2014:414-423.

[9] WU Fei,JING Xiaoyuan,DONG Xiwei,et al.Cost-sensitive local collaborative representation for software defect prediction[C]//International conference on software analysis,testing and evolution.Kunming,China:IEEE,2016:102-107.

[10] 王 晴,荆晓远,朱阳平,等.基于局部稀疏重构度量学习的软件缺陷预测[J].计算机技术与发展,2016,26(11):54-57.

[11] CASTRO C L,BRAGA A P.Novel cost-sensitive approach to improve the multilayer perceptron performance on imbalanced data[J].IEEE Transactions on Neural Networks and Learning Systems,2013,24(6):888-899.

[12] 刘江涛.距离度量学习中的类别不平衡问题研究[D].南京:东南大学,2016.

[13] 王超学,潘正茂,马春森,等.改进型加权KNN算法的不平衡数据集分类[J].计算机工程,2012,38(20):160-163.

[14] SHEPPERD M,SONG Qinbao,SUN Zhongbin,et al.Data quality:some comments on the NASA software defect datasets[J].IEEE Transactions on Software Engineering,2013,39(9):1208-1215.

[15] MENZIES T,GREENWALD J,FRANK A.Data mining static code attributes to learn defect predictors[J].IEEE Transactions on Software Engineering,2006,33(1):2-13.