一种基于EABC的新型搜索方法

辽宁省财政厅信息中心 牛 旭

1.引言

人工蜂群算法对于解决函数优化问题有显著的效果但其也有其缺陷，如易于过早陷入局部最优、后期收敛速度慢、对于复杂的问题搜索最优解能力弱[1]，计算精度不高等问题，针对以上缺陷，对该算法进行优化设计。

2.人工蜂群算法

人工蜂群算法是一种群体智能优化算法，主要思想是模拟蜂群的智能采蜜行为[2]。该算法首先，随机产生初始种群P，SN个初始解，其中SN为采蜜蜂数也等于蜜源数。每个解都是一个D维的向量，D为优化参数的个数。然后，以这些初始解为基础对采蜜蜂、观察蜂和侦查蜂进行循环搜索[2]。

根据蜂源的花蜜量[3]，观察蜂选择每个蜜源的概率为：

其中，为蜂源i的适应值。

已知当前记忆位置，通过下式产生新的候选位置vi，即ABC的搜索方程：

其中，k,j满足k∈{1,2，…,SN}，j∈{1,2,…,D}，k不等于I，为[-1,1]区间内的随机数。

如果蜜源经过指定的循环次数后仍没有改进，则舍弃该位置。该处的采蜜蜂成为侦查蜂并按下式产生新位置。

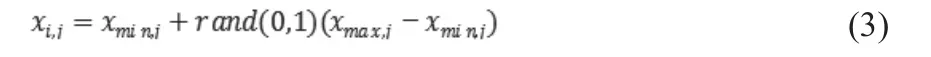
其中，为搜索空间的上界和下界。

3.相关算法

（1）ABC/best算法[4]：相比于标准ABC的搜索方程，ABC/best/1和ABC/best/2产生的候选解只分布在当前种群的最优个体附近。因此，改进的搜索方程具有很强的开发能力。同时，ABC/best算法的结构比较简单易于执行。只要在标准ABC算法框架中更换搜索方程即可。

（2）GABC算法[5]：受粒子群算法的启发，GABC算法采用以下搜索方程：

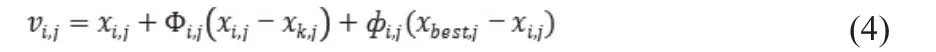
其中，k,j满足k∈{1,2,…,SN}，j∈{1,2,…,D}，k不等于i，为[-1,1]之间的随机数，为[0,1.5]之间的随机数，为当前种群的最优个体。可以看出，受粒子群启发的搜索方程(4)，由于有当前群体的最优个体的引导，在保证算法探索能力的同时，在一定程度上也提高了算法的开发能力。

4.EABC算法

为了更大程度地提高计算精度和收敛速度，本文在研究ABC/best和GABC算法的基础上，提出了新型的基于人工蜂群的EABC算法。以下方程分别为采蜜蜂阶段和观察蜂阶段的搜索方程：

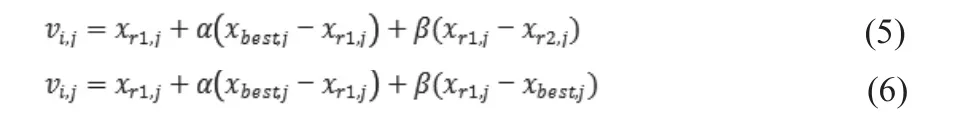
其中，r1,r2,j满足r1,r2∈{1,2，…,SN}，j∈{1,2,…,D}，r1,r2,i互不相等，为当前群体最优个体，α为[0,A]之间的随机数，β为rand*B，这里B是一个均值为μ，方差为σ的高斯分布数。以下给出了EABC算法的伪代码：

Step 1) 初始化:

Step 2) 采蜜蜂阶段:For i=1,...SN,执行以下程序

Step 2.1)采用式(1)产生一个新的候选位解Vi; 计算f(Vi),令FES=FES+1.

Step 2.2)如果

Step 3) 计算概率值Pi,令t=0，i=1.

Step 4) 观察蜂阶段:

While t<=SN,执行以下程序

Step 4.1) IF rand（0,1），产生一个新的候选解Vi; 计算

f(Vi),令

Step 4.2) 令i=i+1,IF i=SN,令i=1.

Step 5) 侦查蜂阶段:

随机产生一个解替换Xi.

Step 6) IF FES>=Max.FES,结束运行并输出最优解,最优个体;ELSE，转至Step 2.

5.测试与分析

5.1 测试函数集及实验参数设置

为比较EABC算法与几种对比算法的性能，本章从文献中选取了11个D=30或D=60的测试函数，1个D=100或D=200的测试函数，2个D=10的测试函数，1个D=4的低维测试函数，1个D=24的测试函数和2个D=30的测试函数。

对所有的测试函数，设置种群的规模为100（SN=50），limit=0.6*SN*D。为了能对算法结果进行有效统计，每个函数独立优化30次，统计其平均最优值（Mean）和标准方差（SD）在对不同算法进行比较时，每个独立运行的算法采用相同的初始群体，这样使得每个算法之间的比较是公平的，实验结果如图1。

图1 各算法运行比较

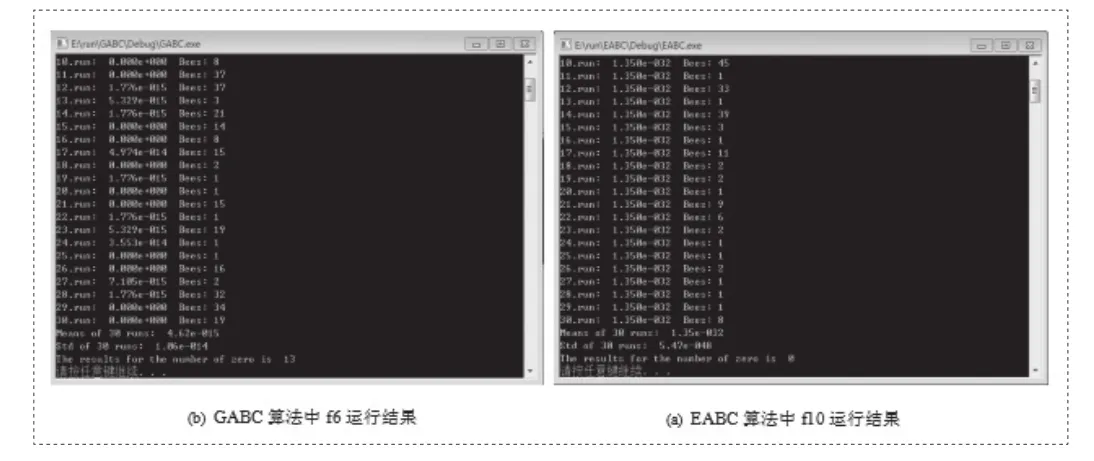
图2 GABC/ EABC算法运行结果

为更直观的反映算法的寻优效果，将EABC算法与标准ABC算法，ABCbest1算法，ABCbest2算法，GABC算法进行比较。五种算法对相关测试函数的收敛曲线如图1所示。由上图可以看出，EABC算法的计算精度和收敛速度比标准ABC算法和GABC算法都有很大程度的提高。ABCbest1算法在多数函数中也取得了较好的结果。

5.2 实验截图

本文的数据是ABC算法, ABC/best/1算法, ABC/best/2算法,GABC算法, EABC算法分别在f1函数, f2函数……, f32函数中实现得到的, 结果如图2所示。

6.结论

本文针对蜂群算法的改进策略及适应性能进行探讨和研究。针对现有算法存在的不足之处，受蚁群算法、差分进化算法、粒子群优化算法的启发，设计出了一些新的搜索方程，提出了改进的EABC算法。相比于标准ABC的搜索方程，EABC通过在采蜜蜂和观察蜂阶段采用不同的搜索方程来提高算法的开发能力。最后，通过数值试验，验证了所提出的搜索方程可以显著地提高人工蜂群算法的性能。使其在保证探索能力的基础上，可以提高开发能力。

[1]江铭焱.人工蜂群算法[M].北京:科学出版社,2015:56-57.

[2]贾俊平.统计学[M].北京:中国人民大学出版社,2015:11-17.

[3]BruceJohnson.VisualStudio2015高级编程(第6版) [M].北京:清华大学出版社,2016:105-108.

[4]申元霞,王国胤.新型粒子群优化模型及应用[M].北京:科学出版社,2016:22-23.

[5]刘新宇.算法新解[M].北京:人民邮电出版社,2016:34-39.