基于Gauss线检测的雪糕棒浅劈裂缺陷识别

沈阳工业大学视觉检测技术研究所 苑玮琦 朱 蕊

0 引言

在雪糕棒的质量检测过程中，劈裂的检测至关重要。因为在雪糕成品的加工中雪糕棒要打入雪糕中心内部，若雪糕棒存在劈裂则会导致在打入的过程中雪糕棒折断[1]。中国是雪糕棒的最大生产国，生产出口量巨大[2]，若存在劈裂的漏检产品将会成批退回造成巨大经济损失。

目前基于图像处理的不同裂纹检测方法主要有：a)阈值分割法，这是最基本的裂纹分割提取方法，但该方法适用于目标区域和背景区域处于不同灰度级范围的图像[3，4]，对于浅劈裂检测存在漏检；b)边缘检测法，该方法可以有效地去除噪声干扰，更好的定位图像的边缘和灰度变化区域，是裂纹缺陷的主要检测方法。

本文针对以上问题，提出了一种基于机器视觉[5，6]的浅劈裂在线检测方法,根据两种浅劈裂情况制定了相应的解决方案：a)通过高斯线检测阈值筛选的准确性实现对裂纹不明显对比度低的浅劈裂的提取，计算其长度进行检测，保证此类浅劈裂的不漏检；b)提取到裂纹不连续的浅劈裂缺陷，计算属于同一直线上的线段总长度，解决此类浅劈裂的漏检问题。

1 雪糕棒浅劈裂缺陷特征分析

劈裂是雪糕棒的表面主要缺陷之一，图1列举了图库中浅劈裂的两种类型。(a)为灰度值对比度小的浅裂纹劈裂。(b)为裂纹不连续浅劈裂，这类劈裂不仅灰度值对比度比较小，且该浅裂纹不连续，出现间断。这两种浅劈裂雪糕棒因为缺陷区域面积很小，不会影响灰度直方图的走势，因此只有背景区域一个波峰。用Canny边缘检测[7，8]提取裂纹时边缘过渡区干扰线条太多，不能准确的区分出劈裂缺陷，容易造成漏检和误检。

图1 浅劈裂雪糕棒

如图2(a)所示为Canny边缘检测算子检测出的缺陷，由于雪糕棒头部边缘过渡区的影响，检测的不够准确干扰过多。相比于Canny边缘检测，高斯线检测如图2(b)所示，对不明显的低对比度浅劈裂检测效果较好。因此本文选择高斯线检测算子来提取雪糕棒对比度低的浅劈裂。

图2 不明显裂纹检测对比图

2 Gauss线检测原理

对于这类缺陷的雪糕棒，主要利用高斯线检测的方法实现其检测。经典的Steger算法[9]是基于Hessian矩阵[10]的一种线检测方法，它能够实现光条中心亚像素的精度定位。首先通过图像与一个高斯掩膜的卷积的偏导数来决定图像中的每个点在x方向和y方向的泰勒二次多项式的参数，进而来获得该点的线条方向和二阶导数极大值，然后再根据双阈值的限定来提取需要的像素点。

首先对图像进行高斯滤波，高斯滤波广泛应用于图像处理的减噪过程，用一个模板(或称卷积、掩模)扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值[11，12]。对图像来说，常用二维离散高斯函数作平滑滤波器，函数表达式如下：

式中σ为高斯分布的标准差，x，y表示的是当前点到对应目标点的距离，常用二维零均值离散高斯函数作平滑滤波器。

要想得到一个高斯滤波器的模板，可以对高斯函数进行离散化，得到的高斯函数值作为模板的系数。如下图3所示要产生一个3 *3的高斯滤波器模板，以模板的中心位置为坐标原点进行取样。模板在各个位置的坐标，如下所示（x轴水平向右，y轴竖直向下），这样，将各个位置的坐标带入到高斯函数公式(1)中，得到的值就是模板的系数。

图3 高斯模板

在图像与高斯模板函数进行卷积后得到偏导数rx，ry，rxx，rxy和ryy，其中rxx表示图像沿x的二阶偏导数，其他参数类似。

然后根据偏导数得到图像的二次泰勒展开形式为：

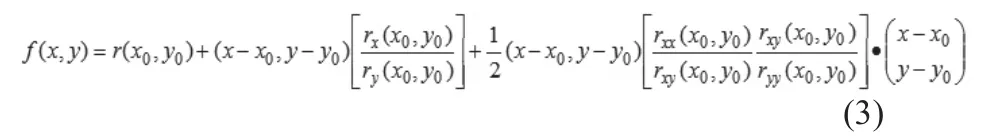
对于图像中任意一点(x,y)，Hessian矩阵可以表示为：

Hessian矩阵最大特征值对应的特征向量对应于线条的法线方向，用(nx, ny)表示，以点(x0, y0)为基准点，则线条的亚像素坐标为：，将其代入到泰勒展开式(3)中得到：

若，即一阶导数为零的点位于当前像素内，即满足沿边缘方向的一阶方向导数为0，下面再求该点的二阶方向导数。通过引入Hessian矩阵，可以计算边缘方向n和这一方向的二阶导数。

Steger算法的初步计算可以得到每一点的方向向量和二阶方向导数，最后根据算法中参数的设定来实现线条的检测。高斯线检测算法的参数为（σ，Low，High），其中σ指定了高斯模板的参数（平滑程度），Low和High为高低阈值参数。如果被标记点的二阶偏导数值大于参数High，其被认为是线条上的点而被立即接受，如果低于参数Low，其被认为不是线条上的点而被立即舍弃，如果其大于参数Low但小于参数High，则仅在此点能够通过某一路径与已经被接受的点相连时这些点才被接受。关于参数的选择，σ越大，图像的平滑程度越大，二阶导数越小，因此在选择高低阈值的时候，平滑程度越大，所选择的High和Low值就要越小。

3 基于Gauss线检测的雪糕棒浅劈裂缺陷特征提取

3.1 雪糕棒浅劈裂候选像素的粗提取

雪糕棒浅劈裂候选像素的提取是将裂纹从雪糕棒图像上分离出来，准确的提取出雪糕棒浅劈裂是保证劈裂缺陷质量正常检测的前提，提取结果的准确性和精确性都将对雪糕棒浅劈裂能否准确检测起到关键作用。为了减少高斯线检测算子的运行时间，提高运行速度，且劈裂缺陷都在雪糕棒头部，因此进行了雪糕棒头部区域的粗略定位，如图4所示。

图4 雪糕棒头部区域

本文提出高斯线检测对裂纹进行提取，

由第2节分析可知，高斯线检测的效果由三个参数所决定，其中σ代表着数据的离散程度，如图5所示。

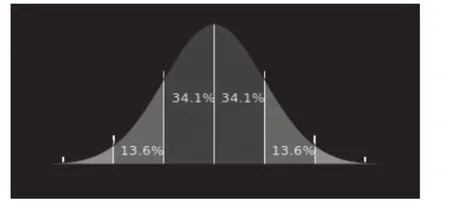
图5 一维高斯分布的概率分布密度图

横轴表示可能的取值x，竖轴表示概率分布密度F(x)，这样一个曲线与x轴围成的图形面积为1。σ（标准差）决定了这个图形的宽度，可以得出结论：σ越大，则图形越宽，尖峰越小，图形较为平缓；σ越小，则图形越窄，越集中，中间部分也就越尖，图形变化比较剧烈。因此σ若大，则图像的平滑程度越大，会造成细裂纹的漏检，经过劈裂缺陷图库的验证，经过实验选择σ为0.8。

Low和High阈值的选择，受σ的影响，σ越小，图像的平滑程度越小，二阶导数越大，因此在选择高低阈值的时候，平滑程度越大，所选择的High和Low值就要越小，经过图库实验验证，检测的阈值选择为2和12。（0.8,2,12）的阈值能够提取到雪糕棒浅劈裂条纹，保证了缺陷的不漏检，但同时会存在部分因矿物线和纤维丝状所造成的误检，如图6所示，分别为高斯线检测提取后存在的情况示意图。

图6 浅劈裂候选像素提取示意图

为了解决干扰线条的影响，进行后面的缺陷的筛选。

3.2 雪糕棒浅劈裂缺陷的筛选

得到候选像素后，要对所提取到的缺陷区域进行判断，对判断为劈裂的雪糕棒进行后续的检测、分级，对不是劈裂缺陷的雪糕棒跳出算法进行其他缺陷的检测。

对于裂纹对比度低的浅劈裂雪糕棒，对其的判断首先对检测出的像素线段进行简单的长度筛选，将小像素干扰排除掉，对去除小线段干扰的像素线段进行相邻像素的连通，如图7所示。

图7 缺陷筛选过程示意图

由于劈裂缺陷都从头部开始延伸，为排除因位置关系所提取到的误检像素线，利用相交性算子判断提取出的候选像素是否与头部边缘相连接或计算候选像素距离头部边缘的距离，如下图8(a)所示弧线为经过采集图片的实验验证将头部边缘轮廓向内移动10个像素后的轮廓线。进而与候选像素进行位置的判断，即判断候选像素与边界的连通性，如图8(b)所示，图中弧线和裂纹线段存在交点则认为存在连通性，认为该相交线段为劈裂缺陷。最后计算存在边缘连通性候选像素点的个数，排除头部其他缺陷的误检情况，如图9所示，头部存在多个奔头的条纹，计算交点数量大于等于3则不认为其为劈裂缺陷，利用此判断减少头部线段干扰造成的误检。

图8 劈裂缺陷的判断

图9 奔头干扰示意图

对于裂纹不连续的浅劈裂，由于断裂的缘故可能会与雪糕棒头部轮廓线没有交集或存在于距离头部轮廓线较远的位置，经过验证在判断连通性的检测时，将轮廓线向内移动参数为50个像素值来进行连通性判断，进而依照上面方法排除头部多线段干扰，得到图10(c)所示缺陷示意图，然后分别计算图中三个线段各点像素的平均行坐标，比较三个线段的平均行坐标波动情况，判断这些线段是否在同一条直线上，波动值经过采集缺陷图片分析，设置为4个像素，在同一直线上下波动的线段筛选为缺陷线段。

图10 不连续裂纹筛选示意图

4 缺陷质量检测

根据第1节的分析可知，雪糕棒浅劈裂分为裂纹对比度低、不明显劈裂和裂纹不连续、断裂劈裂，通过第3节对两种类型缺陷候选像素的提取和筛选，已经得到了以上两种浅劈裂的目标缺陷区域。针对于以上两种情况的特征提出了相应的质量检测方案。

针对低对比度的浅劈裂雪糕棒，利用最小外接矩形算子计算目标缺陷的裂纹长度，根据表1劈裂缺陷的判定标准对裂纹进行等级判定。

针对不连续的浅劈裂雪糕棒，计算符合条件的各个断裂线段的最大最小列坐标，其中k为符合条件的线段个数，选择中的最大值与最小值做差作为待检测的裂纹长度，根据表1劈裂缺陷的判定标准对裂纹进行等级判定，其中E为缺陷条纹像素个数。

表1 雪糕棒劈裂缺陷质量分级规则

5 实验结果与分析

5.1 算法测试平台

以114型雪糕棒[13]为实验对象，114型雪糕棒的长度为114.0mm，宽度为9.6mm，厚度为2.0mm。为了验证本文算法，在雪糕棒的检测过程中采集了图像，建立了雪糕棒劈裂缺陷图库。图11为采集图像的装置图，采集设备为USB接口CCD相机，型号为MQ013MG-E2。调节好相机的焦距，光圈，和传送带之间的距离后让雪糕棒以每秒10支的速度，传送带带动雪糕棒运动，使雪糕棒逐一传送至成像位置，进行图像的采集。整幅图像分辨率为256×1280，实验所用计算机处理器为i7 6700K ，主频3.6GHz，计算机内存8GB，编程工具为VS2010。

图11 图像采集装置

5.2 系统标定实验

由于相机精度和设备存在机器误差，采集到的图像会存在一定的变形，现通过系统标定获得标定系数使雪糕棒空间上点和图像像素点实现正确的变换。本文使用Tsai两步标定法[14，15]来进行标定。

(a)选择20mm长度的刻度尺。

(b)固定好相机和光源，调整好相机的焦距和光圈到能清晰拍摄检测到雪糕棒的状态并将其锁定。保证相机、光源的位置不变，光源的亮度不变，将刻度尺放在拍照时雪糕棒所在的位置上，同时拍摄雪糕棒和刻度尺，利用图像处理算法统计出雪糕棒总像素点所占用的刻度尺的长度为105mm。

5.3 实验结果

为了进一步说明算法的检测效果，对建立的图像库图片进行检测，图库中共有600幅缺陷图片，其中裂纹明显连续的普通劈裂缺陷200幅，裂纹对比度小的浅劈裂200幅，裂纹不连续的浅劈裂图片200幅。利用本文的检测算法和Canny边缘检测方法对劈裂缺陷图库进行了测试，测试检测结果如表2所示。

由表2可见，本文方法的优点在于，高斯线检测的提取，不但解决了雪糕棒浅劈裂的漏检问题，且能根据缺陷区域的空间形态特征来进行筛选判断，减少了误检的情况，从而可以获得更好的检测效果。对于Canny边缘检测方法的缺陷检测率有相应的提高，检测正确率提高了8.34%。

表2 本文方法与其他方法的检测性能对比

对于检测失败的两根雪糕棒，其裂纹缺陷处闭合紧密，与普通的雪糕棒相比，缺陷处灰度变化不明显，导致漏检。如图12所示。

图12 检测失败图例

6 结论

雪糕棒劈裂是雪糕棒中比较严重且对雪糕棒成本造成损失的缺陷，劈裂缺陷中普通劈裂缺陷利用Canny边缘检测便可检测出劈裂缺陷，但裂纹不明显不连续的浅劈裂缺陷利用此方法不能准确提取到缺陷。针对此情况提出本文的检测算法，对裂纹不明显不连续的浅劈裂缺陷进行了高斯线检测搜索和筛选，利用其空间形态特征判断是否为同一直线上线段，同时阐述了算法的详细步骤，在自己建立的图库下进行实验验证，并且检测准确率相比Canny边缘检测方法提高了8.34%，达到了99.67%，说明了本文所建立的检测方法性能优良，也说明了本文的检测方法对该缺陷检测的有效性。

[1]马文生.雪糕棒是这样生产出来的[N].中国国门时报,2007-08-23(001).

[2]苑玮琦,李德健,李绍丽.雪糕棒轮廓质量视觉在线检测方法[J].计算机应用研究,2016,33(10):3185-3190.

[3]阳天舒,李梅,信荟敏,赵永红.基于形态学的自适应阈值分割算法[J].电子设计工程,2015,23(13):102-104.

[4]Alamri S S,Kalyankar N V,Khamitkar S D.Image Segmentation by Using Threshold Techniques[J].Computer Science,2010,2(5).

[5]郭静,罗华,张涛.机器视觉与应用[J].电子科技,2014,27(07):185-188.

[6]颜发根,刘建群,陈新,丁少华.机器视觉及其在制造业中的应用[J].机械制造,2004(11):28-30.

[7]许宏科,秦严严,陈会茹.一种基于改进Canny的边缘检测算法[J].红外技术,2014,2014,36(03):210-214.

[8]Kewen Liu,Kang Xiao,Hongxia Xiong.An Image Edge Detection Algorithm Based on Improved Canny[P].2017 5th International Conference on Machinery,Materials and Computing Technology(ICMMCT 2017),2017.

[9]王巧妮,杨远洪.基于Steger图像算法的光纤布拉格光栅寻峰技术[J].光学学报,2014,34(08):133-138.

[10]冯瑶,刘宁,冯亚崇.一种针对造影图像中血管狭窄的自动识别技术[J].生物医学工程学杂志,2013,30(02):380-386+394.

[11]王耀贵.图像高斯平滑滤波分析[J].计算机与信息技术,2008(08):79-81+90.

[12]Wang H Y,Fei Z H,Wang X L.Precise simulation of star spots and centroid calculation based on Gaussian distribution[J].Optics &Precision Engineering,2009,17(7):1672-1677.

[13]王玉春.雪糕棒生产工艺简介[J].林业科技开发,1993(03):22.

[14]徐杰.机器视觉中摄像机标定Tsai两步法的分析与改进[J].计算机工程与科学,2010,32(04):45-48+58.

[15]Zhang Z.A Flexible New Technique for Camera Calibration[J].Tpami,2000,22(11):1330-1334.