液滴在不同润湿性表面上蒸发时的动力学特性∗
2018-06-19叶学民张湘珊李明兰李春曦
叶学民 张湘珊 李明兰 李春曦
1 引 言
液滴蒸发是制造工业中的常见现象,处于蒸发状态下的液滴在固体壁面上的运动特性与焊接、农药喷洒和喷墨打印质量密切相关[1−4].基底材质、表面粗糙度和润湿性[5]通过改变液滴运动过程中的接触角和三相接触线[6−8],从而影响液滴的动力学特性[9,10].深入研究其对液滴运动影响的内在机理有助于调控液滴运动,进而改进工艺和提高产品质量.
在实验方面,Mollaret等[11]研究了不同基底加热温度下铝和聚四氟乙烯表面上液滴蒸发的动态过程,发现基底温度较高时呈现接触线钉扎模式下的蒸发过程.Kuznetsov等[12]针对由Al2O3制成的固体基底上的纯水和盐水液滴的蒸发过程,指出浓度为9.1%的盐水液滴蒸发过程中呈现接触线钉扎模式,而浓度达到16.7%时则呈现接触线移动模式下的铺展过程.Kiper等[13]对比了环境压力为1—101 kPa时疏水和超疏水基底上的液滴蒸发动态特征,指出接触角随压力升高而减小;在较低压力下,液滴将从Cassie-Baxter状态转变到Wenzel状态.Lopes和Bonaccurso[14]探究了黏弹性基底上液滴的蒸发过程,发现通过调整基底柔软度可控制接触线钉扎模式和恒定接触角模式间的转变.Gatapova等[15]在基底与环境温差为40◦C的条件下分析了壁面润湿性对液滴蒸发的影响,指出液滴运动过程中接触线呈现钉扎、部分钉扎和去钉扎3种模式;且在液滴存续的最后阶段,蒸发速率急剧增加.Guan等[16]发现放置在光滑纹理表面上的液滴蒸发过程遵循理想的恒定接触角模式,底面纹理的存在对蒸发起抑制作用.Kuznetsov等[17]分析了不同粗糙度铜基板表面上的液滴蒸发过程,指出改变基底粗糙度可调控液滴铺展历程.张文彬等[18]通过观测含SiO2颗粒的液滴蒸发后在固体表面上的环状沉积图案,发现液滴蒸发过程中的接触线钉扎是形成环状沉积的必要条件.
理论研究方面,早期对液滴蒸发过程的理论研究多基于预置液膜模型.Ajaev等[19]研究了在加热倾斜平面上重力驱动的挥发性液膜流动过程中表观接触角的静态值和动态值,指出静态接触角随温度升高而增大.Karapetsas等[20]模拟了不溶性表面活性剂和非相互作用的颗粒存在时液滴蒸发的动态特性,发现活性剂通过抑制接触线的移动进而减缓蒸发过程.值得注意的是,采用预置液膜模型时,液滴并非与固体表面接触,因此无法探究壁面润湿性对液滴蒸发过程的影响.为此,近年来有学者研究液滴与固体表面直接接触时液滴蒸发的动态特征.Bouchenna等[21]研究了接触线钉扎时液滴的蒸发速率和内部的流动模式,指出可忽略热浮力效应对液滴内部流动的影响;在蒸发的最后阶段,接触线处蒸发速率的影响才变得重要;热毛细力主要控制蒸发过程中液滴内部的流动模式.Amini和Homsy[22]通过建立接触线钉扎和具有恒定接触角不同蒸发模式下的理论模型,模拟了光滑加热基底上二维挥发性液滴的形态演变历程,指出尽管随时间推移,液滴厚度的减小使蒸发质量增加,但蒸发质量的总和与液滴的总面积变化使接触线在后退过程中以几乎恒定的速度移动.
上述关于处于蒸发状态的液滴在固体表面上的动力学特性研究虽然涉及壁面性质的影响和以接触线、接触角为代表的壁面因素,但均未阐释壁面润湿性影响接触线动态特征的物理机制,目前也鲜有这方面的文献报道.为此,本文采用滑移边界条件,建立受热蒸发的液滴在固体表面上的二维演化模型,通过数值模拟探讨液-气、固-气和液-固界面张力温度敏感性对壁面润湿性和液滴蒸发过程的影响,揭示壁面润湿性对不同接触线运动模式影响的内在机理.
2 理论模型
2.1 物理模型
如图1所示,一液滴放置在加热的固体表面上并不断蒸发,液滴初始最大厚度为H∗,流动方向尺度为L∗,壁面温度为T∗w.由于ε=H∗/L∗≪1,因此可应用润滑理论[23]进行解析(上角标∗表示有量纲量,下同).
液滴运动过程的控制方程包括连续方程、动量方程和能量方程:

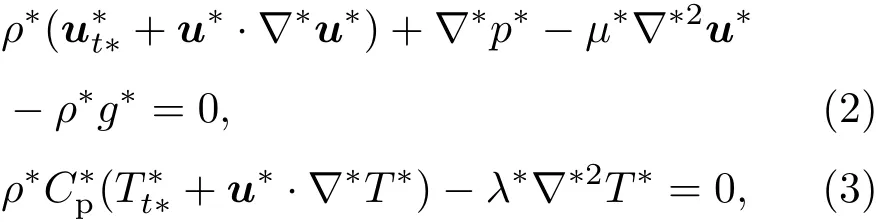
式中 p∗,T∗和t∗分别表示压强、温度和时间;µ∗和ρ∗分别为液体动力黏度与密度,λ∗为液滴导热系数,C∗p为液体的定压比热,∇∗为梯度算子;u∗=(u∗,w∗),u∗和w∗分别为水平和垂直方向上的速度分量.
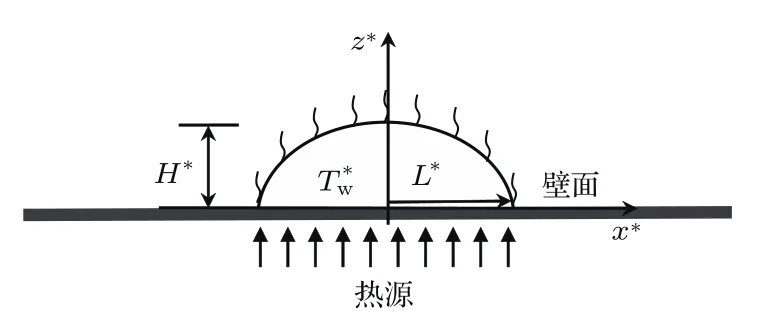
图1 放置在加热表面上的液滴示意图Fig.1.Schematic of drop disposed on a horizontal heated substrate.
在液-气界面处,满足切向和法向应力平衡:
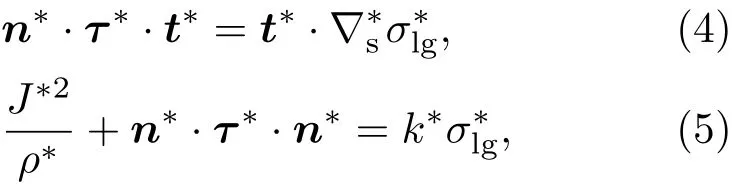
式中分别为界面处的单位法向和切向向量,h∗为液滴厚度;k∗= −∇∗·n∗为液-气界面处的平均曲率,τ∗= −p∗I∗+ µ∗(∇∗u∗+ ∇∗ut∗)为总应力张量,J∗为界面质量迁移的质量跃变流率,σl∗g为液-气界面张力.
在液-气界面处,运动学及热边界条件为

式中L∗a为气化潜热.
界面处的蒸发流量与界面温度有关,其方程为

式中为界面热阻;T∗i为界面温度,Ts∗为液体的饱和温度,R∗g为通用气体常数,Mm∗为单分子质量,ρ∗v为蒸气密度,a为协同因数.
壁面温度满足

假设界面张力与温度满足线性关系[8]:

式中为相应界面在T0∗下的界面张力,为温度引起的张力梯度;T∗0和T∗i分别为参考温度和界面温度;lg,ls和sg分别代表液-气、液-固和固-气界面.
将控制方程和边界条件采用下式进行无量纲化:

式中为特征速度,为铺展系数,λ∗h为液-气界面处液体的导热系数,Tm∗表示液滴的最高温度,为相应界面在Tm∗下的张力,Σi(i=lg,ls,sg)为相应界面张力对温度的敏感系数.
通过无量纲变换并保留数量级大于等于O(ε),可得无量纲控制方程组为:
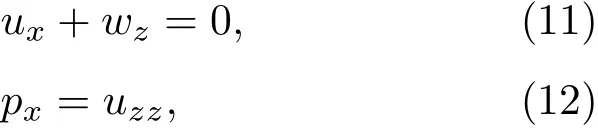

式中为邦德数,下角标表示对该参数求偏导.
无量纲边界条件为:

式中分别表示毛细数、滑移系数、加热系数和蒸发数,β∗为滑移长度.
由(17)式和(22)式可得
无量纲形式的界面张力与温度关系为

采用积分法可得液滴厚度的演化方程为
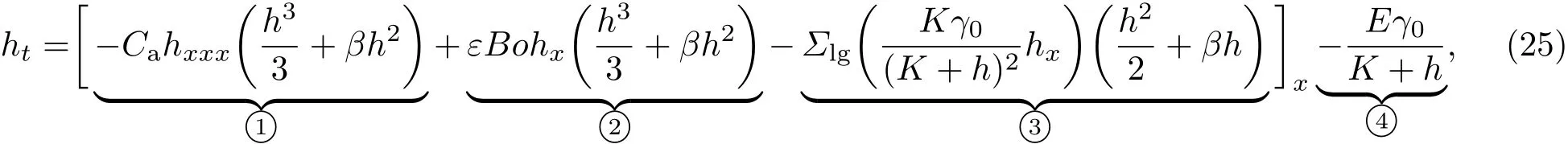
(25)式右侧依次代表毛细力、重力、热毛细力和蒸发在液滴运动过程中的作用.当K=E=0,可简化为Karapetsas等[24]所建模型.
接触线处的液滴高度为零,即h(x=xcl=xcr,t)=0,其中xcl和xcr分别代表左侧和右侧接触线的位置,采用下式描述接触线移动速率与接触角间的关系[24]:

式中 B和q为常数,忽略接触角滞后现象,θ和θa分别为液滴的动态接触角和平衡接触角.υc>0代表向外铺展,υc<0则代表向内收缩.
在接触线处,Young方程为

由于在液滴铺展中θa很小,故采用Karapetsas等[24]的假设:cosθa→ cos(εθa); 又有1 − (ε2θ2a)/2 ≈ cos(εθa),因此可得

式中A=σsg,0−σls,0−1.当(28)式右侧为负时,取θa=0,表示壁面“完全润湿”.
2.2 初始条件和网格选取
计算初始条件为

式中H(x)= 0.5[1+tanh(20x)]为Heaviside函数[25].
模拟中采用Karapetsas等[24]所提方法,把液滴运动区域采用坐标变换的方式固定在[−1,1];采用Freefem软件,计算中将[0,2]×[0,1]的计算域划分为500×2个均匀网格.因方程是一维的,液滴厚度与y方向无关,所以为节约计算时间在y方向仅划分2层网格.计算中时间步长为10−6.模拟中,在x方向上对比了网格数为300,500和700的结果,表明当网格数为500时可同时满足精确性与高效性的要求.
3 结果与讨论
Σlg,Σsg,Σls表征液-气、固-气和液-固界面张力对温度的敏感性.为探究界面张力影响壁面润湿性和液滴运动过程的内在机理,下文分别讨论上述3个敏感性系数在液滴蒸发中的作用.参照Mollaret等[11]和Gatapova等[15]的实验,可得液滴基本参数的取值范围(表1),由此可推出模拟所用无量纲参数的取值范围(表2).如无特殊说明,取值如下:ε=0.1,B=0.001,q=3,σls,0=1,A= −0.001,Bo=0.5,β =1×10−5,γ0=0.1,Ca=0.1,K=10,E=1×10−3.

表1 有量纲液滴的基本参数取值范围Table 1.Typical range of dimensional parameters of drop.

表2 液滴的无量纲参数取值范围Table 2.Range of dimensionless parameters of drop.
3.1 相同的界面张力温度敏感性
当Σlg= Σls= Σsg=1时,其平衡接触角θa=0.447为定值,即此时壁面呈现均匀润湿特征(图2和图3).因液滴运动在x=0两侧呈对称形式(图2(a)),下文以右侧接触角、接触线为例来阐明其动态过程.如图(2(b))所示,液滴演化过程大致分为3个阶段:I)t=0—1.0×104为铺展阶段;II)t=1.0×104—2.55×104为接触线钉扎阶段;III)t=2.55×104—3.4×104为液滴直径和接触角同时减小、直至被蒸干阶段.

图2 液滴演化过程 (a)轮廓;(b)接触线;(c)最大高度Fig.2.Evolution of drop with time:(a)Profi le;(b)contact line;(c)maximum thickness.
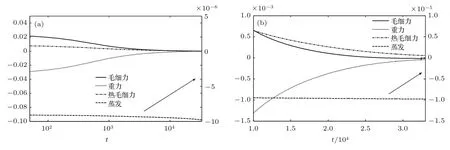
图3 液滴演化过程中的各作用项影响 (a)整体过程;(b)阶段II和IIIFig.3.Eff ect of items during evolution of drop:(a)Entire process;(b)stage II and stage III.
由(25)式可知,液滴运动历程受毛细力、重力及热毛细力和蒸发等因素的影响.由图3可知,重力对液滴铺展起促进作用,而毛细力、热毛细力则起抑制作用.整个运动过程中,随时间持续,毛细力、重力和热毛细力对液滴厚度变化的影响在降低,而蒸发对液滴厚度减少的影响在增强.图2(a)和图2(c)表明,在阶段I,液滴厚度最大时下降最快,此时重力占主导作用,且在阶段I时毛细力对铺展的抑制作用比热毛细力和蒸发更显著(图3(a));在阶段II和III,热毛细力对铺展的抑制作用超过毛细力的影响(图3(b)).因液滴表面温度与液滴厚度成反比,随液滴铺展其表面温度增加,且接触线处的温度最高,所以液滴蒸发量由最大厚度处到边缘处逐渐增大.因此,在阶段II接触线呈现钉扎现象,是由于重力、毛细力与热毛细力等3项作用之和对液滴接触线处的质量补充与蒸发携带走的质量达到平衡所致;而在阶段III接触线呈现去钉扎特征,是由于此时3项作用之和对液滴接触线处的质量补充已不能弥补蒸发携带走的质量.
Mollaret等[11]将初始直径约为3.25 mm的水滴放置在加热到60◦C的铝表面进行蒸发实验,将其所得接触角变化的实验结果采用文中所给无量纲变换式进行变换后,与本文模拟值进行对比,如图4所示.图4表明,模拟值与实验结果趋势相同、符合良好,但实验结果中并未包含液滴铺展阶段,因此无法呈现阶段I的特征.接触角变化的斜率大于模拟值是实验所用加热温度高于模拟值所致.
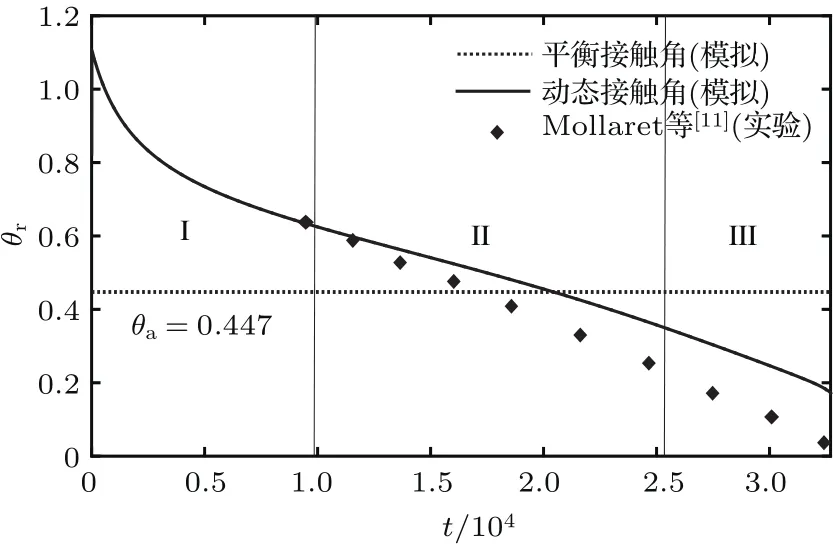
图4 接触角变化的模拟值和实验值对比Fig.4.Comparison of variation of contact angle with time between simulated and experimental results.
3.2 不同界面张力温度敏感性
3.2.1 液-气界面张力温度敏感性
取Σlg=1.005和1.008,其他参数不变,以体现液-气界面张力敏感系数的影响.液滴演化历程如图5—图7所示.由(25)式可知,液-气界面张力系数发生变化时,将改变液滴所受热毛细力,且由图3可知,增大Σlg,即增大热毛细力,可抑制液滴铺展过程.
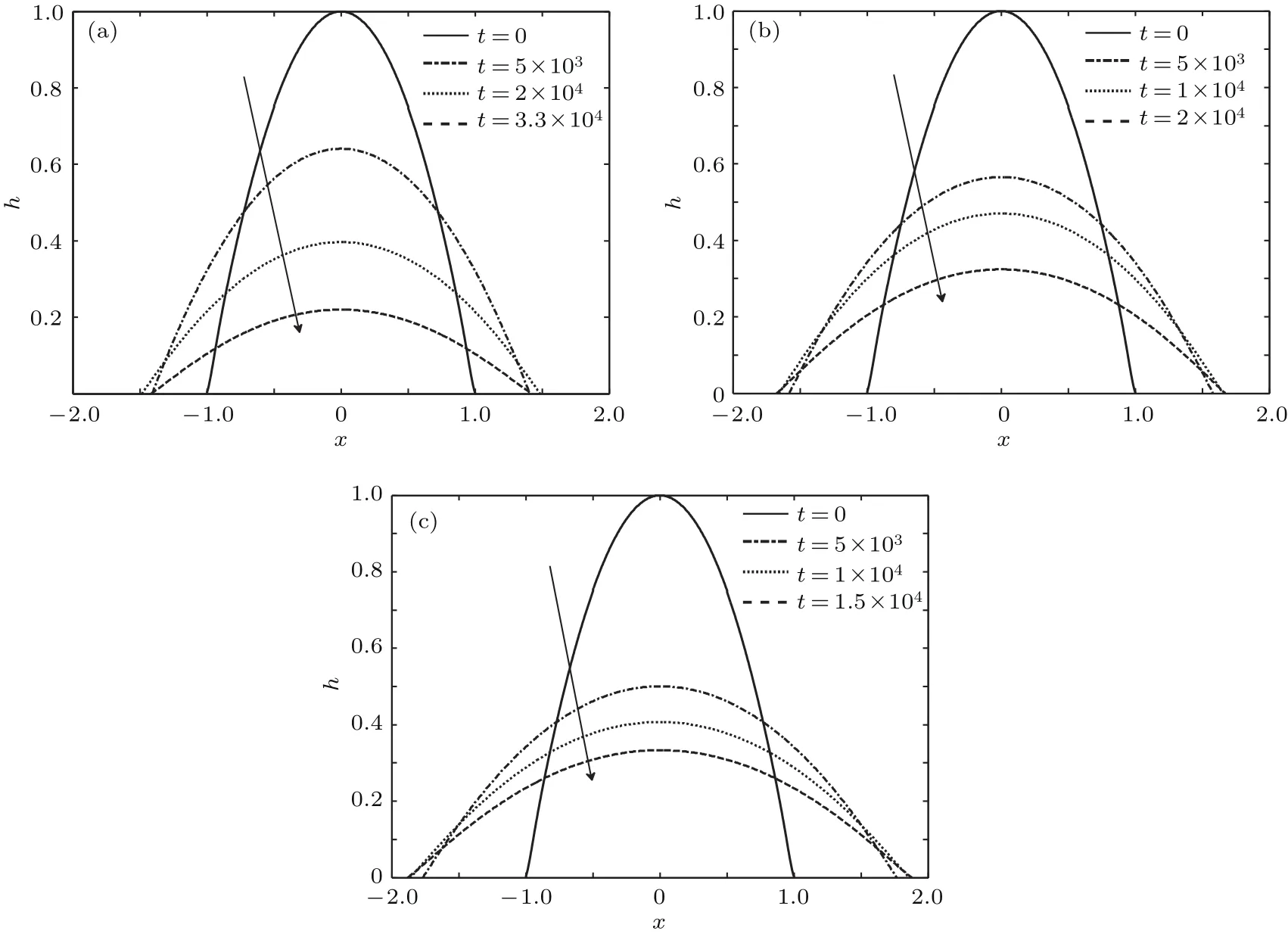
图5 液滴轮廓变化 (a)Σlg=1.0;(b)Σlg=1.005;(c)Σlg=1.008Fig.5.Evolution of drop profi le with time:(a)Σlg=1.0;(b)Σlg=1.005;(c)Σlg=1.008.

图6 不同Σlg时接触线变化 (a)位置;(b)速度Fig.6.Changes of contact line with diff erentΣlg:(a)Location;(b)velocity.

图7 不同Σlg时液滴的演化过程 (a)接触角;(b)直径Fig.7.Evolution of drop with diff erentΣlg:(a)Contact angle;(b)diameter of the drop.
由(28)式可得,此时的平衡接触角分别为θa=0.2982和0.1491,即增大Σlg,将减小液滴在固体壁面铺展时形成的平衡接触角,进而提高其壁面润湿性能.液滴内部流体的水平方向速度为
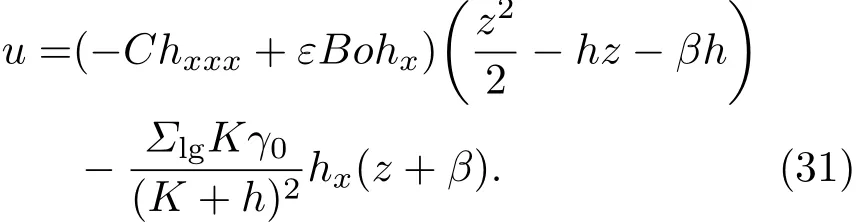
(31)式表明,提高Σlg可增大u,即提高液-气界面张力敏感系数可加速液滴铺展.当Σlg=1.005和1.008时,接触线达到钉扎的时刻分别为t=1.41×104和1.51×104,如图6(a)所示.因此,提高液-固界面张力敏感系数后形成的较小平衡接触角将推迟接触线达到钉扎现象的出现.
Σlg=1.005和1.008时,接触线xcr与t的幂律关系分别为xcr≈t0.041和xcr≈t0.059,即上述作用的综合结果提高了液-气界面张力敏感系数Σlg,进而显著加快了液滴的铺展速度(图5和图6),并使液滴厚度加快减薄.因液滴表面温度与其厚度呈反比,此时液滴表面温度得以提高,而蒸发速率与液滴表面温度呈正比,故提高液-气界面张力系数可增大液滴表面的蒸发速率.该情形下液滴的蒸干时间分别为t=2.39×104和1.64×104,相对于Σlg=1.0的情形,Σlg=1.005和1.008时液滴蒸干时间分别缩短了30%和52%.虽然Σlg仅改变了0.5%和0.8%,但却对液滴铺展和蒸发过程产生了显著影响.
3.2.2 固-气界面张力温度敏感性
为探讨固-气界面张力敏感系数的影响,将Σsg增至1.005和1.008,其他参数不变.此时的平衡接触角分别为θa=0.650和0.745,即提高固-气界面张力敏感性系数Σsg可增大平衡接触角,致使液滴在壁面上的润湿效果变差.模拟显示,这两种情形下的液滴蒸干时间分别为t=6.94×104和7.8×104,相对于Σsg=1.0,其蒸干时间分别延长了104%和129%.由图8可知,同一时刻下(t=1×104),液滴铺展速度明显减慢,因液滴表面温度与其厚度呈反比,此时液滴表面温度降低,而蒸发速率与液滴表面温度呈正比,故提高Σsg可减慢液滴表面的蒸发速率.Σsg=1.005,1.008时接触线达到钉扎状态的时刻分别为t=8×103,7×103(图9).由此可知提高Σsg可使接触线提前达到钉扎状态.
下文以Σsg=1.005,即平衡接触角θa=0.650时做具体分析.图10为液滴的接触线钉扎蒸发模式与恒定接触角蒸发模式.由图11(a)和图11(b)可知,液滴演化过程经历4个阶段:I)t=0—8×103迅速铺展阶段;II)t=8×103—3.5×104接触线钉扎、接触角减小阶段;III)t=3.5×104—6.7×104接触线去钉扎、 接触角近似恒定阶段;IV)t=6.7×104—6.94×104液滴直径和接触角同时减小、直至被蒸干阶段.阶段I和阶段IV的时间较短,而阶段II和阶段III时间相对较长,且二者大体相当.这与Semenov等[4]总结出的液滴在固体壁面蒸发的4个阶段特征相符合(见图11(c)和图11(d)).
Gatapova等[15]在控制基底与环境温差为40◦C的情形下,采用初始体积为92.6µL,直径为4.5 mm的水滴在涂有六甲基二硅氮烷的表面进行蒸发实验.类似于3.1节,将其所得接触角和接触线的实验数据无量纲化后与模拟值进行对比,如图11(a)和图11(b)所示.该图表明,文中所得模拟值与Gatapova等[15]实验结果总体符合良好,即模拟结果可反映液滴在主要阶段的典型特征.但值得注意的是,Gatapova等[15]的实验结果并未呈现液滴铺展阶段与最后的蒸干阶段,前者是因接触角迟滞作用的影响所致,而后者的可能原因是受此阶段变化较快、不易观测记录影响.
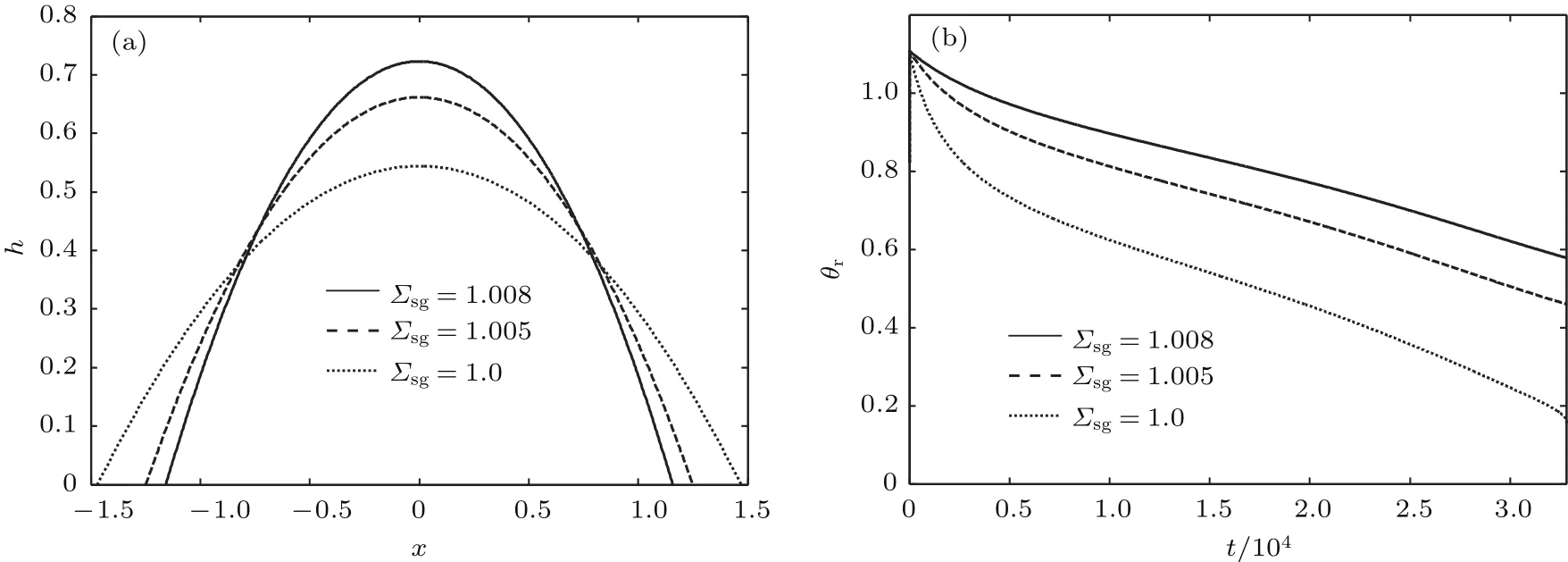
图8 液滴演化过程 (a)轮廓;(b)接触角Fig.8.Evolution of drop with time:(a)Profi le;(b)contact angle.
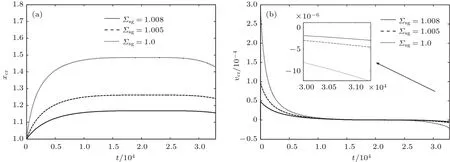
图9 接触线变化 (a)位置;(b)速度Fig.9.Changes of contact line with time:(a)Location;(b)velocity.
在3.2.1节中,液滴接触线并未出现去钉扎现象就已被蒸干,从而未呈现本节提到的阶段III和IV,这是由于与较大的Σlg相比,较大的Σsg对接触线的影响更加明显,所以接触线的动力学特征受Σsg影响更为显著,在工业应用中可利用此特性调控接触线的移动过程来满足实际需要.此结论与Gatapova等[15]使用不同润湿性的基底对液滴蒸发进行控制,从而观察到接触线钉扎、部分钉扎、去钉扎现象的实验结果符合.
为进一步分析液滴演化过程中的内流特征,图12给出了不同时刻下液滴内部的速度与流线. 内部流动大致可为3个阶段. 1)t=0—6.7×104,流线由液滴内部指向边缘处.但t=0—8×103接触线处的水平速度为正,表明此时液滴处于阶段I,如图12(a)和图12(b)所示.当t=0.8×104—3.5×104时,接触线处的水平速度为零,表明此时液滴处于阶段II;当t=3.5×104时接触线处的水平速度为负,表明此时液滴开始出现接触线去钉扎,即开始进入阶段III,如图12(c)所示.2)t=6.7×104—6.9×104,回流阶段.t=6.7×104时,可发现液滴内部靠近接触线处流线出现回折,而在t=6.8×104时可看到明显的回流,表明此时液滴处于阶段IV.3)t=(6.9—6.94)×104,流线由液滴边缘处指液滴内部.此时液滴内部的流线已经完全改变方向,表明液滴已接近阶段IV的最后时刻.

图10 液滴轮廓变化 (a)接触线钉扎阶段;(b)接触线去钉扎阶段Fig.10.Evolution of drop profi le with time:(a)Contact line pinning process;(b)contact line de-pinning process.
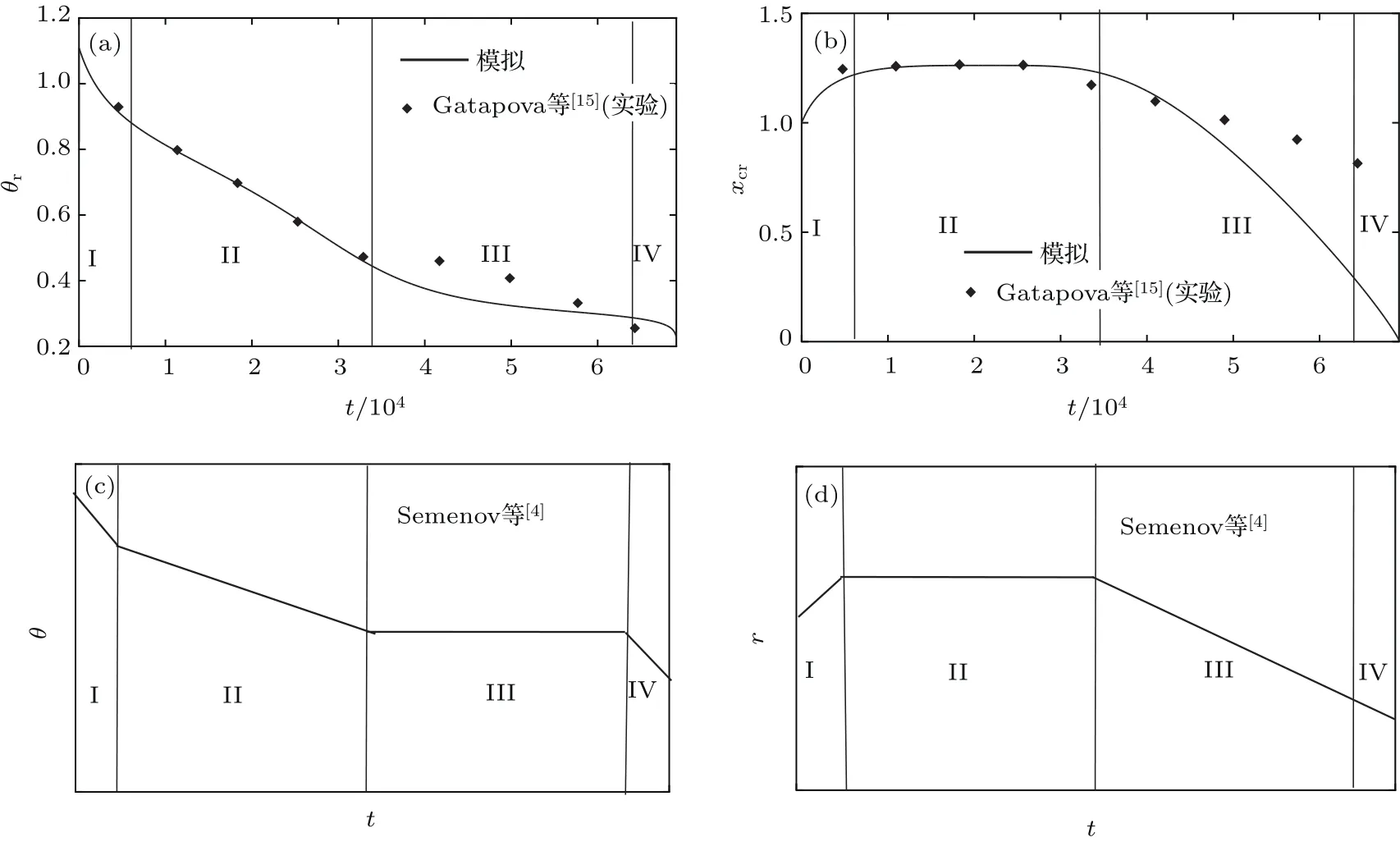
图11 接触角和接触线随时间的变化Fig.11.Changes of contact angle and contact line with time.

图12 不同时刻下液滴内部的流线与水平方向分速度 (a)t=2.0×103;(b)t=8.0×103;(c)t=3.5×104;(d)t=6.7×104;(e)t=6.8×104;(f)t=6.9×104Fig.12.Horizontal velocity contour within the drop along with streamlines at diff erent time:(a)t=2.0×103;(b)t=8.0×103;(c)t=3.5×104;(d)t=6.7×104;(e)t=6.8×104;(f)t=6.9×104.
3.2.3 液-固界面张力温度敏感性
将3.1节中的Σls=1.0增至Σls=1.005和1.008,其他参数不变进行分析.此时的平衡接触角分别为θa=0.2981和0.1490,与Σlg=1.005和1.008时相比,平衡接触角值仅在小数点第4位有差别,因此该情形下的液滴运动过程与3.2.1节中几乎完全相同,由此可知Σls和Σlg对壁面润湿性能的影响总体相同.而Σsg变化0.5%和0.8%时的影响则非常显著,因此通过改变固-气界面张力温度敏感系数调控处于蒸发状态下的液滴运动更加有效.
4 结 论
液滴运动过程中受毛细力、重力、热毛细力及蒸发等因素的影响,重力对液滴铺展起促进作用,而毛细力和热毛细力则起抑制作用.随时间持续,毛细力、重力和热毛细力对液滴厚度变化的影响逐渐降低,而蒸发对液滴厚度减少的影响则逐渐增强.界面敏感性系数是影响液滴运动过程的重要因素,通过改变界面张力温度敏感系数,可使液滴蒸发过程中的接触线呈现钉扎或部分钉扎模式下的动力学特征.
当界面张力温度敏感性相同时,液滴演化过程呈现3个典型阶段:1)铺展阶段;2)接触线钉扎阶段;3)液滴直径和接触角同时减小、直至被蒸干阶段.而界面张力温度敏感性不同时,则呈现不同的液滴演化过程和动力学特征.当Σlg> Σsg= Σls或Σls> Σlg= Σsg时,演化过程呈现两个典型阶段:1)铺展阶段;2)接触线钉扎阶段.与Σls=Σsg=Σlg时相比,该情形下的平衡接触角减小,壁面润湿性能得以改善,进而提高液滴铺展速率,延长接触线达到钉扎状态的时间,增大液滴蒸发速率和缩短液滴存续时间.
当提高Σsg(Σsg>Σls=Σlg)时,液滴演化过程呈现4个典型阶段:1)铺展阶段;2)接触线钉扎阶段;3)接触线去钉扎且接触角近似恒定阶段;4)液滴直径和接触角同时减小、直至被蒸干阶段.与Σls=Σsg=Σlg时相比,该情形下平衡接触角增大,壁面润湿性能恶化,致使液滴铺展变慢,接触线达到钉扎的时间缩短.因此,通过改变固-气界面张力温度敏感系数调控处于蒸发状态下的液滴运动更加有效.
[1]Saada M A,Chikh S,Tadrist L 2013 Int.J.Heat Mass Transf.58 197
[2]Li C X,Yang B C,Ye X M 2015 Chin.J.Theor.Appl.Mech.47 71(in Chinese)[李春曦,杨保才,叶学民 2015力学学报47 71]
[3]Kavehpour P,Ovryn B,Mckinley G H 2002 Colloids Surf.A 206 409
[4]Semenov S,Trybala A,Agogo H,Kovalchuk N,Ortega F,Rubio R G,Starov V M,Velarde M G 2013 Langmuir 29 10028
[5]Erbil H Y 2012 Adv.Colloid Interface Sci.170 67
[6]Zang D,Yu Y,Zhen C,Li X,Wu H,Geng X 2017 Adv.Colloid Interface Sci.243 77
[7]Sefi ane K 2006 J.Petrol.Sci.Eng.51 238
[8]Ye X M,Li Y K,Li C X 2016 Acta Phys.Sin.65 104704(in Chinese)[叶学民,李永康,李春曦 2016物理学报 65 104704]
[9]Zhu J Y,Duan Y Y,Wang X D,Min Q 2014 CIESC J.65 765(in Chinese)[朱君悦,段远源,王晓东,闵琪 2014化工学报65 765]
[10]Sefi ane K 2004 J.Colloid Interface Sci.272 411
[11]Mollaret R,Sefi ane K,Christy J R E,Veyret D 2004 Chem.Eng.Res.Des.82 471
[12]Kuznetsov G V,Feoktistov D V,Orlova E G 2016 Thermophys.Aeromech.23 17
[13]Kiper I,Fulcrand R,Pirat C,Simon G,Stutz B,Ramos S M M 2015 Colloids Surf.A 482 617
[14]Lopes M C,Bonaccurso E 2012 Soft Matter 8 7875
[15]Gatapova E Y,Semenov A A,Zaitsev D V,Kabov O A 2014 Colloids Surf.A 441 776
[16]Guan J H,Wells G G,Xu B,McHale G,Wood D 2015 Langmuir 31 11781
[17]Kuznetsov G V,Feoktistov D V,Orlova E G,Batishcheva K A 2016 Colloid J.78 335
[18]Zhang W B,Liao L G,Yu T X,Ji A L 2013 Acta Phys.Sin.62 196102(in Chinese)[张文彬,廖龙光,于同旭,纪爱玲2013物理学报62 196102]
[19]Ajaev V S,Gambaryan-Roisman T,Stephan P 2010 Colloid Interface Sci.342 550
[20]Karapetsas G,Sahu K C,Matar O K 2016 Langmuir 32 6871
[21]Bouchenna C,Saada M A,Chikh S,Tadrist L 2017 Int.J.Heat Mass Transf.109 482
[22]Amini A,Homsy G M 2017 Phys.Rev.Fluids 2 043603
[23]Zhao Y P 2012 Phys.Mech.Surf.Interface(Beijing:Science Press)pp185–186(in Chinese)[赵亚溥 2012 表面与界面物理力学(北京:科学出版社)第185页—186页]
[24]Karapetsas G,Sahu K C,Matar O K 2013 Langmuir 29 8892
[25]Craster R V,Matar O K 2000 J.Fluid Mech.425 235
