基于最大似然的单通道交叠激光微多普勒信号参数分离估计∗
2018-06-19郭力仁1胡以华1王云鹏1徐世龙1
郭力仁1)2) 胡以华1)2)† 王云鹏1)2) 徐世龙1)2)
1 引 言
在对运动目标进行遥感探测时,目标发动机振动、叶片转动等微运动的存在会对回波信号产生附加的频率调制,产生所谓的“微多普勒效应”[1].典型的目标如坦克、汽车、飞机等都有自己独特的微动形式和特定的微动参数范围[2,3],通过准确地提取微多普勒特征和精确估计微动参数可以实现对目标的分类和精确识别.就发动机引起的振动而言,目标的振动幅度往往在微米量级甚至更小.由于微多普勒调制效应与波长成反比[4],一般雷达探测很难获得明显的微动特征,所以激光探测微多普勒效应在准确反演目标特征和精确估计微动参数中就有着不可替代的优势.
微多普勒效应的应用关键在于目标微动参数的精确估计.在激光探测中,经常存在多目标或目标等效为多个散射点的情况,而且目标微动参数往往比较接近[5],在补偿了目标的主体运动后,回波信号就成为单通道多分量(single channel multicomponent,SCMC)时频域交叠的混合信号,目前还没有有效的估计方法.对SCMC微多普勒信号的研究主要分为非参数化和参数化两类[6].前者主要基于时频分析方法,由于从时频分布图(timefrequency distribution,TFD)上可以直接对瞬时频率变化规律进行观察,便于理解,使其成为过去十几年间研究提取微多普勒特征的主要方向.但是多分量的时频分布受交叉项和窗函数的影响严重[7],改进的时频分析方法[8,9]提高了时频分辨率,但计算过程复杂,运算量大.从包含多个分量的TFD中提取微动特征,传统方法如峰值提取等[10]不再适用.文献[11]根据微动瞬时频率(instantaneous frequency,IF)曲线平滑无跳变的特点,提出基于Viterbi的曲线跟踪类方法,可以逐次提取时频域上混叠的多条IF曲线,但该类方法对信噪比要求较高,对曲线断点、交点处的处理性能差,且严重依赖前面时频分析的效果.文献[12]采用Radon变换从TFD中估计微动参数,提高了算法的鲁棒性,但是这类方法只能将参数定位到一个模糊的区域,估计精度无法保证,而且模型仅适用于两参数估计的情况,参数增多计算量将呈指数增加,不适合对实际中的多参数情况进行分离和估计.
为提高目标微动参数的估计精度,近几年来参数化方法开始兴起.文献[13]提出循环平稳方法,估计了微动频率,但由于信号长度及循环周期性的限制,无法避免出现1/2或双倍周期的估计误差,不适合多分量信号.文献[14]提出基于高阶矩的方法估计微动参数,虽然较图像处理和正交匹配等方法耗时短,但依然不具备实时处理能力,且鲁棒性较差.文献[15]和文献[16]则提出了正弦调频匹配空间滤波法,通过依次估计各分量参数,对信号进行重建,实现分离,但其在参数估计中采用网格搜索,导致估计精度和计算量存在不可调和的矛盾.文献[17]提出基于粒子滤波的SCMC参数估计,但是对于多分量多参数的情况,对粒子数量要求量巨大,难以保证多维粒子的理想更新.文献[18—20]分别引用盲源分离、总体经验分解、局域均值分解等信号处理方法,这对于多通道或频域不混叠的多分量微多普勒信号有一定效果,但是对SCMC这种极端欠定情况或时频域存在交叠的信号则无法有效分离.Setlur等[21]基于最大似然估计的框架提出了迭代加权非线性最小二乘估计方法,得到了近似克拉美罗下界的估计精度,但算法步骤复杂,每次迭代计算量很大.最大似然方法已被证明是一种无偏渐进最优估计[22],在数据足够多、信噪比较高时,MLE的性能可达到估计下界,远高于常用的非参数化方法.但是,目前的似然函数都是面向雷达信号建立,对于适用于微弱振幅探测的激光微多普勒信号,传统方法构建的似然函数非线性程度急剧增加[23],似然函数分布形状由平滑的单峰变为密集的多峰[24],使传统迭代类或统计类的MLE在具体实现中无法得到有效的收敛.
为了从激光探测得到的单通道多分量且时频交叠信号中精确估计目标微动参数,本文提出基于奇异值分解和最大似然框架的微动参数分离估计方法.通过精细化扫描信号周期点数,改进了信号矩阵的构建方法,使基于奇异值比(singular value ratio,SVR)谱的微动频率估计精度得到了数量级上的提高;分析对比了激光与微波探测微弱振幅微多普勒信号的特点,基于频域能量分布设计了新的似然函数,在效果上相当于对传统似然函数分布进行了平滑,而且由于噪声在频域上均匀分布,利用频谱能量构建似然函数有效提高了算法的抗噪性能;利用均值思想给出了最大似然估计的解析表达,并用马尔可夫-蒙特卡罗(Markov Chain Monte Carlo,MCMC)采样方法解决了估计中的高维积分问题,实现了对参数进行联合估计,提高了算法效率,同时避免了误差传递问题.用该算法对仿真和实验数据进行处理,得到了接近克拉美罗界的参数估计精度,验证了算法的可行性.通过与传统基于时频分布的逆Radon变换得到的估计结果对比,体现了本文方法在精确估计混合微动参数上的优势.
2 单通道多分量激光微多普勒信号模型
根据电磁散射理论,电大尺寸目标在光学区的散射具有局部效应,目标总的电磁散射可等效为一些局部散射点的叠加,这些局部的散射源就叫作等效散射中心.对于激光探测的目标微多普勒效应回波信号,其波长远小于目标尺寸,采用电磁散射在光学区的等效散射中心理论是合理的.
Chen[4]基于散射中心模型对振动、转动、锥动等典型微动的微多普勒效应建立了回波数学模型.经过后续化简和整合,这些微动的散射中心模型都具备基本的正弦调频形式.对于实际探测中常遇到的单通道多目标或目标具有多个等效散射中心的多分量情况,包含微多普勒效应的基带信号离散形式可写为
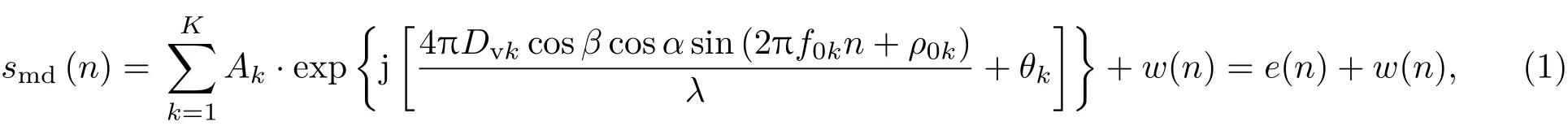
式中 λ表示激光波长;f0k=fvk/fs,fs为采样率;Dvk,fvk,ρ0k分别表示目标第k个散射中心对应的微动幅度、频率、初始相位;Ak和θk表示信号强度和初相;K 表示回波中叠加的分量个数;e(n)表示无噪声干扰信号;w(n)为噪声;α,β是目标相对于雷达的方位角和俯仰角,对于目标微动参数来说是慢变化量,在信号处理过程中认为是常数.另外考虑到激光探测发散角较小,认为照射光斑内各散射点的α,β相同.为简便起见,在计算过程中可将散射点振动方位角和俯仰角,目标方位角和俯仰角都设为0.
3 时频交叠激光微多普勒信号的参数分离估计
3.1 基于SVR谱的微动频率估计
根据奇异值分解理论,若矩阵S的各个行向量间的比值为一个常数,则S的奇异值中只有第一项不为0.所以对于周期信号,若将其构建为矩阵形式,则当矩阵每行长度与信号周期长度接近时,奇异值比σ1/σ2就会是一个较大值.奇异值比谱方法就是通过不断改变构建矩阵的列数,寻找最大的σ1/σ2来实现对信号周期的检测[25].激光微多普勒信号具有正弦调频信号的形式,调制信号的周期性使回波基带信号也具备周期性,所以具备通过奇异值比谱法来估计调制周期的条件.
如果直接用完整的信号构建矩阵,矩阵列数与信号周期之间的误差会随着行数增加不断累加,这常常会导致SVR方法失效.所以,这里提出固定列数的周期扫描的改进方法来实现周期的估计.构建矩阵可写为
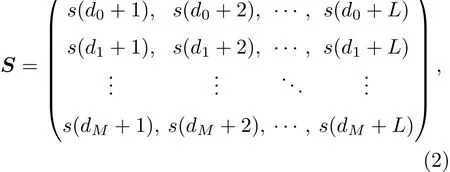
式中dm=round(m·d),d为假设的一个周期内的点数,根据实际情况在目标微动周期的范围[Tmin,Tmax]内对d进行扫描,构建不同列数的矩阵;m=0,1,···,M,M=floor(N/d)−1,表示总信号长度N内包含的周期数;L为每个周期内截取的固定长度,可取L=round(d)以充分利用信号信息.通过SVR估计的信号周期为
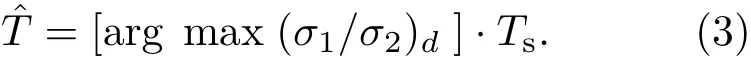
(3)式表示取奇异值比最大时对应的d作为周期长度,ˆT代表估计值,Ts=1/fs表示采样时间间隔.若d在扫描中取整数,即扫描步长∆d=1,则周期估计误差范围在[0—Ts/2],可见信号采样率越高,则估计误差越小.对于确定fs的信号,为进一步减小估计误差,可减小∆d,经过取整运算后,SVR中可能存在最大值对应连续多个位置的情况,则取其中间位置作为最终的点数估计.对应的微动频率为

对于包含多个微多普勒分量的回波信号,若各分量幅度相似,则一次SVR可估计出各分量的微动频率;若各分量信号幅度相差较大,则一次SVR只得到主周期分量的微动频率,继续估计该分量剩余其他参数后,从回波信号中将其重构信号去除,用同样方法可估计其他分量的微动频率.通过仿真得到各分量信号幅度比与SVR峰值比的关系如图1所示.

图1 分量幅值比和SVR峰值比的关系Fig.1.Relationship between the signal amplitude ratio and the peak ratio of SVR spectrum.
图1 中纵坐标SVR1和SVR2分别表示奇异值比谱中周期较长的分量和周期较短的分量对应的峰值大小(即σ1/σ2的值),横坐标代表SVR1和SVR2对应分量的幅值比.当信号幅值比超出图中范围时,SVR中只有一个明显的峰值.图1的关系可为下一节中设计适合激光微多普勒信号的似然函数提供参数选择的依据.
3.2 基于最大似然的微动幅度和初相估计
在3.1节估计了主周期分量微动频率的基础上,继续利用MCMC方法搜索估计该分量的微动幅度和初相,用ψ=[Dvk,ρ0k]T表示第k个分量的微动参数矢量.MCMC是产生服从特定概率分布的样本,所以首先对参数的概率密度函数进行分析.
3.2.1 激光微多普勒信号的均值似然函数
认为(1)式中的噪声是服从N(0,σ2)的加性高斯白噪声,那么信号矢量服从s∼N(µ(ψ),C(ψ)),信号的概率密度函数可写为[26]:
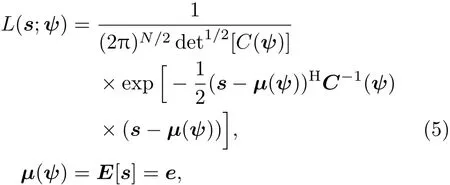
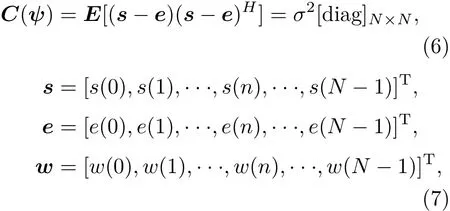
L(s;ψ)即为待估计参数的似然函数,可对其求对数进行化简,
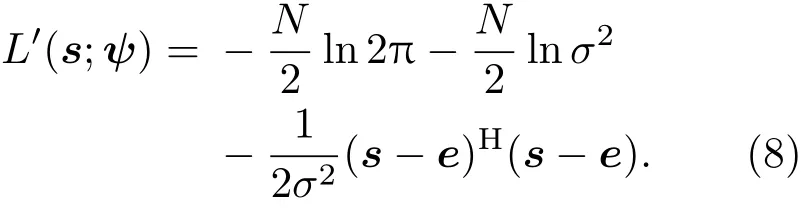
(8)式中,等号右边前两项为常数项,求似然函数的最大值等同于求第三项的最小值,此时参数的似然估计值为:
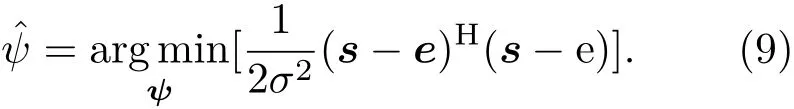
令J(ψ)=(s−e)H(s−e)/2σ2,把信号e分解为振幅项和相位项两个部分,(9)式可改写为:
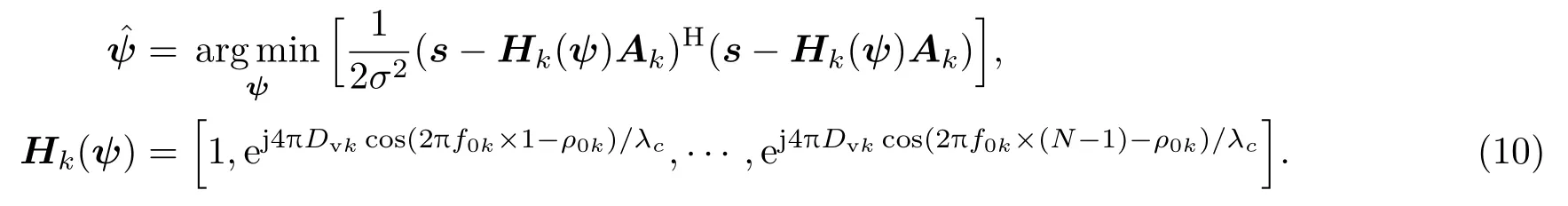
在求解(10)式时,Hk(ψ)和Ak的估计过程解耦分别进行估计与直接求联合MLE是等价的.利用加权最小二乘估计A[24],有

将(11)式代入(10)式得到
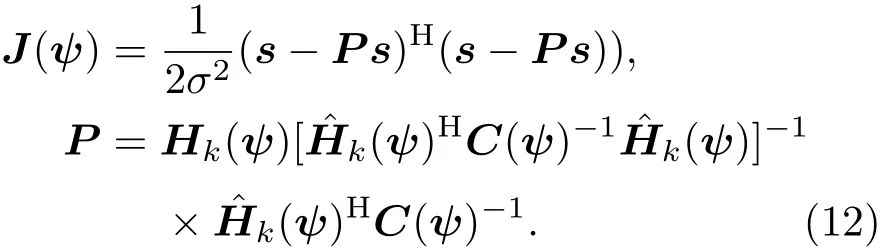
因为P=P2=PH,所以(12)式可化简为
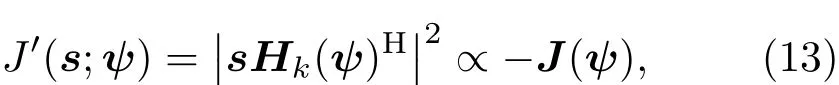
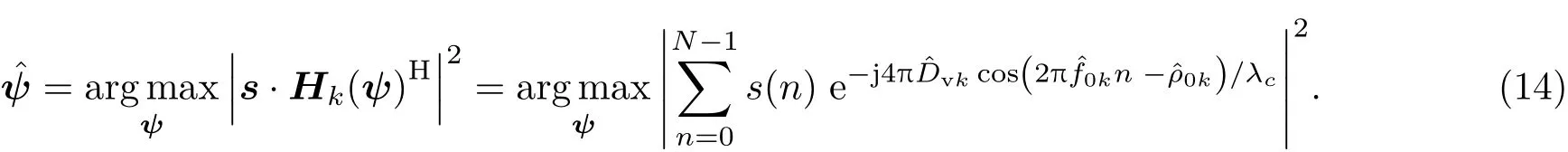
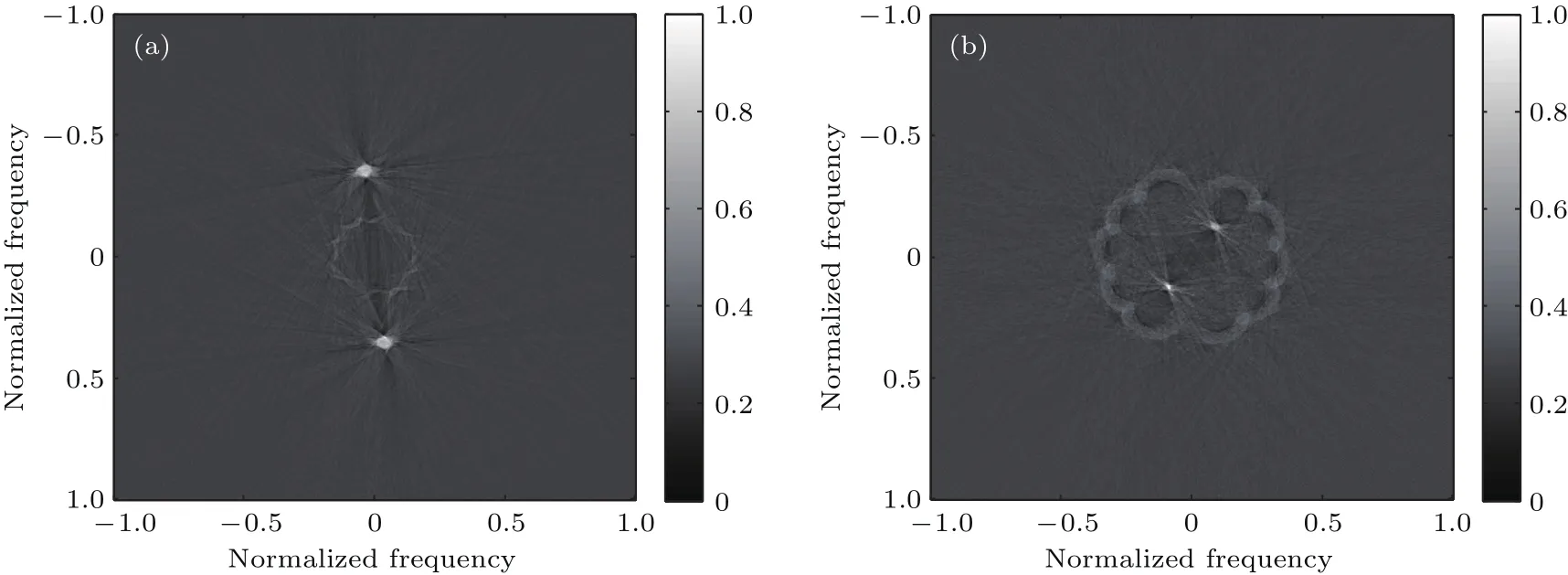
一般直接用(14)式的似然函数形式构建参数ψ的概率分布函数,再用MCMC方法产生服从分布的样本实现对参数的最大似然估计,这对于传统微波探测或是平稳信号处理是可行的.但是对于激光微多普勒信号,由于探测波长极短,信号由雷达探测中的弱调制变为深度调制,似然函数的非线性程度急剧增加,概率分布变为复杂的多峰形状.这将导致马尔可夫链在产生平稳分布时会错误收敛至局部最大值,最终估计错误.微多普勒信号参数估计概率分布与探测波长之间的关系如图2.
图2中的振动幅度设置为5µm,与实验中目标实际振动幅度量级相同.图2(a)为激光波段下的似然函数,其分布为密集的多峰形状.随着波长的增加似然函数峰值分布由密变疏,如图2(a)—图2(d)所示.类似图2(c)平滑的单峰的似然函数可以保证传统的迭代搜索方法实现对参数的高精度估计,但在图2(a)所示的似然函数下,这些方法将失效.此外,随着波长的进一步增加,似然函数峰值消失,这意味着过长的波长失去了对微弱振动的探测和估计能力.所以,处理激光信号时需要对似然函数进行改变.以两分量为例对(14)式中的似然函数进行分析:

图2 不同波长下传统似然函数分布 (a)λ=10−6 m;(b)λ=10−5 m;(c)λ=10−4 m;(d)λ=10−3 mFig.2.Traditional PDF distribution in diff erent wavelength:(a)λ =10−6 m;(b)λ =10−5 m;(c)λ =10−4 m;(d)λ =10−3 m.
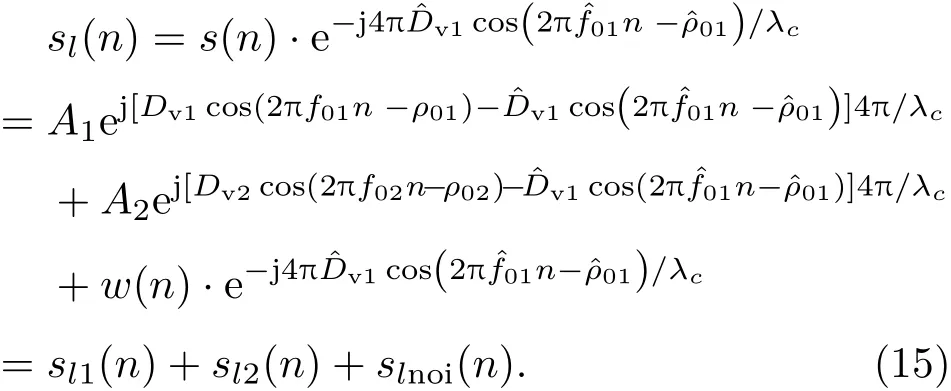
首先通过SVR方法确定出一个分量的微动频率ˆf01,并以此作为先验信息计算Dv1和ρ01参数域上的似然函数分布.当估计值ˆDv1和ˆρ01与信号分量1实际的参数值接近时,sl1(n)的频谱能量集中在零频附近很窄的带宽里,能量峰值极高;而此时,由于分量2与分量1的微动参数不同,在参数域中sl2(n)的频谱能量只能分布在一个较宽的带宽内;slnoi(n)则均匀分布在整个频谱中.当估计值完全与实际值相同时sl1(n)为常数,频谱为冲击响应形状.所以,可以把似然函数频谱中占总能量的比例为η时的能带宽度作为评价参数估计值是否接近真值的标准,构建新的似然函数,

式中F{·}表示傅里叶变换,分母为计算频谱总能量,η为设定sl1(n)部分占总能量的比例,W表示E[sl1(n)]所占频带宽带.由于信号时域和频域能量守恒,η的表达式可写为
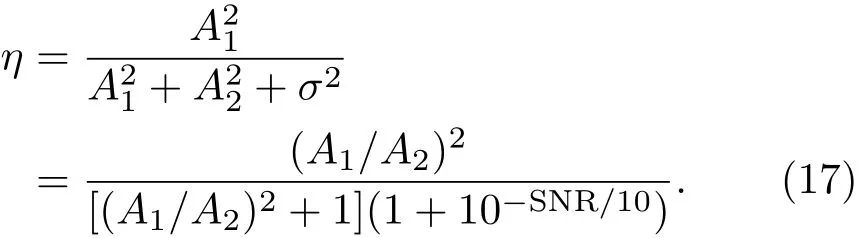
A1/A2的值可根据图1中的关系进行确定.新似然函数各分量频谱关系和参数示意如图3所示.
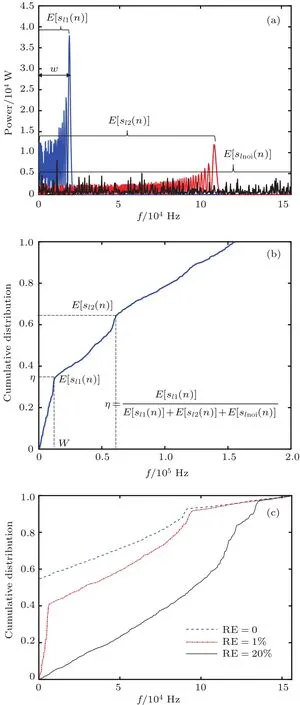
图3 改进似然函数 (a)参数示意图;(b)频谱能量累积分布函数;(c)不同相对误差(RE)下的对比Fig.3 The improved likelihood function:(a)The schematic diagram of parameters;(b)cumulative distribution on spectrum energy;(c)comparison between diff erent relative error(RE).
图3 (b)为图3(a)的累积分布,图中参数估计值与真实值的相对误差为5%,信噪比为5 d B.图3(c)对比结果说明随着相对误差的减小,E[sl1(n)]对应的宽度W也将逐渐减小,所以用W反映参数估计的精度是合理的.由于噪声在频域上均匀分布,利用频谱能量构建似然函数避免了个别时刻噪声的突起对传统基于时域构建似然函数的影响,有效提高了算法的抗噪性能.这时,引入均值似然估计给出多参数MLE的解析表达形式:
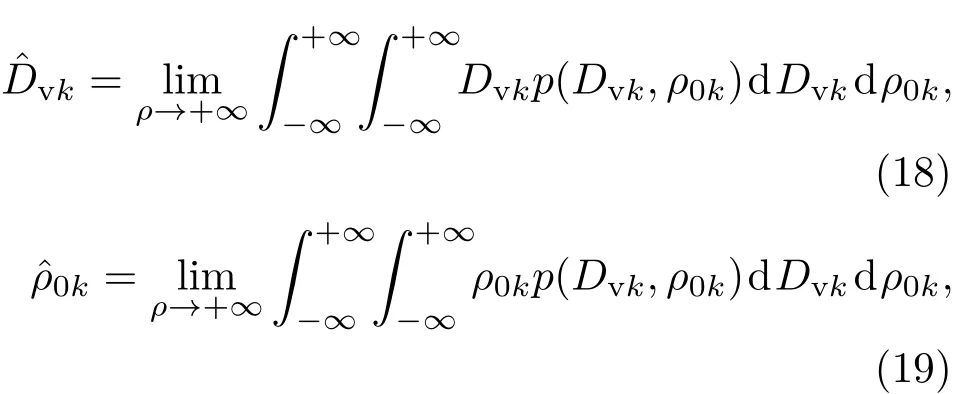
式中p(Dvk,ρ0k)为归一化压缩似然函数,其表达式为
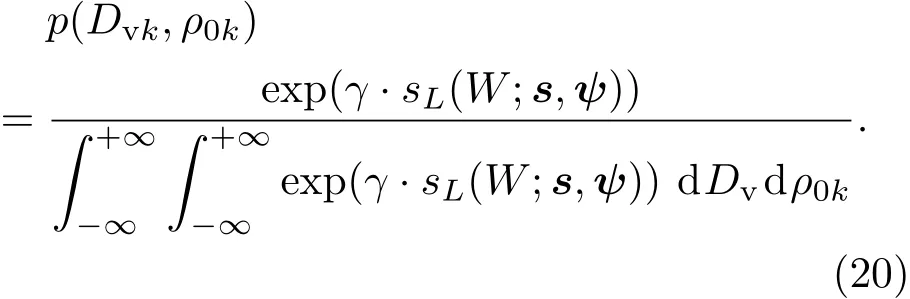
由于(16)式对似然函数形式进行了改进,得到了平滑单峰形状的分布,不再需要专门设置压缩指数γ来突出全局最大值以保证收敛,降低了工作量,这里γ取1.
3.2.2 MCMC算法实现
对于多维参数的MCMC抽样,采用Gibbs方法来具体实现.用π(x)表示目标分布函数,x=(x1,···,xm)是m维参数矢量,q(x)表示建议分布函数. 在产生马尔可夫链的过程中,t时刻第i个参数的状态xti根据条件建议分布q(→ x∗i|) 转移到状态x∗i, 产生t+1时刻的候选样本,=(,···,,,···,);样本的接受概率A(→ x∗i);产生服从0—1均匀分布的随机数u与A(→|)比较,若u小于接受概率,则马尔可夫链t+1时刻状态更新为,否则=.接受概率由概率转移函数的细致平衡等式推出[27]:
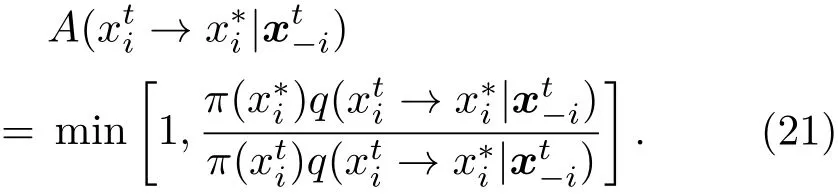
当候选状态使目标分布概率密度增大时,以概率1更新为这个状态,否则,以概率π(x∗i)/π(xti)进行更新.所以,t+1时刻状态的实际转移概率为
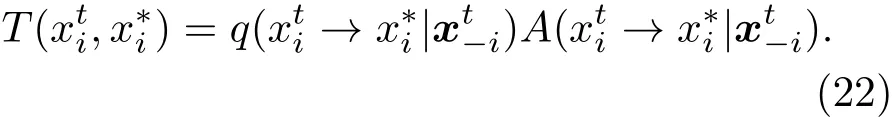
由于T(xti,x∗i)满足细致平衡条件,所以在足够多次的迭代后,马尔可夫链最终将收敛于目标分布π(x).将(20)式作为目标概率分布,对激光微多普勒参数ψ进行似然估计的MCMC算法具体实现步骤为:
1)初始化[D1vk,ρ10k];
2)t时刻,根据条件建议分布的转移概率得到参数 ρ0k的候选状态 ρ∗0k;
3)计算接受概率
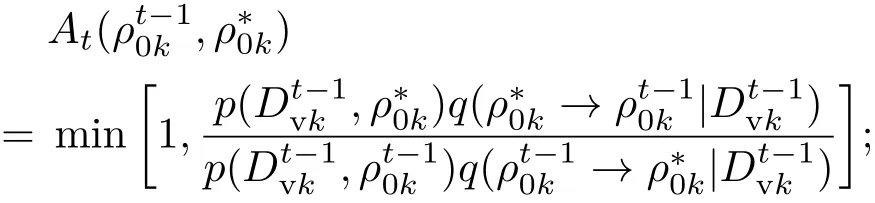
4)产生u ∼ U(0,1), 若u 5)根据条件建议分布的转移概率得到参数Dvk的候选状态D∗vk; 6)计算接受概率 7)产生u′∼ U(0,1),若则 8)将步骤(2)—(7)重复M次,将达到收敛之前的τ−1个样本矢量burn-in,对剩下的样本求均值得到参数的估计为 和 算法建议分布q(x)的选择直接决定了马氏链的收敛效果.若q(x)分布过于分散,则马氏链长期得不到更新,需要很多次迭代才能搜索到最优值,降低算法效率;若分布过于集中虽然能使接受概率高,但每次状态更新跨度太小,同样需要大量的迭代才能实现马氏链的收敛.Gelman等建议将接受概率控制在0.15—0.5比较合适,所以具体操作中可通过对接受概率的监视来调制. 根据3.1节和3.2节估计的第k分量的微动参数重构信号 则(13)式的似然函数形式可改写为 式中 表示观测混合信号中的第k个分量单位调制信号.当估计值与实际参数相等时,重构分量与实际分量抵消,等式最右边第一项等于AkN exp(jθk);由于重构分量与其他分量参数不同,所以第2项相当于是一个宽带正弦调频信号求和,在一个调制周期内其值正好为0,N的值一般根据SVR结果选取整周期长度;噪声和重构信号不相关,经过长时间累积后,第3项也近似为0.此时,可得到信号幅度和相位的估计为: 估计了信号幅度和相位后得到了分量k所有参数,可重建k分量ˆAkˆsk(n)ejˆθk,将其从初始混合信号中去除,用同样方法继续对剩余信号参数进行估计.完整的SCMC混合信号参数估计和分离流程如图4所示. 图4 SCMC激光微多普勒信号分离和参数估计流程Fig.4.The fl ow chart of the estimation and separation method for the SCMC signal. 克拉美罗界(Cramer-Rao bounds,CRB)是所有无偏估计方法所能达到的估计方差的下限,其取值只与信号本身有关,不受估计方法的影响,经常被用作评价参数估计精度的标准.对于矢量参数的CRB,由Fisher信息矩阵求逆后的对角线元素确定,即 式中var(ˆψi)表示第i个参数估计的方差;ψ表示包含待估计微动参数的矢量;I(ψ)为Fisher信息矩阵,其定义为[28] 将微多普勒信号模型代入(28)式,可得到各参数的Fisher信息为: (29)式—(31)式构成微动参数的Fisher信息矩阵I(ψ),其中ω0=2πfv/fs,对I(ψ)求逆可得到参数的CRB.上式中的Fisher信息取值与波长成反比,这意味着CRB与波长成正比.所以,探测中的波长越短,参数估计的CRB越低,能够达到的估计的精度也就越高,这证明了激光微多普勒探测较微波探测在精确估计上具有优势. 以两分量混合的单通道时频域交叠激光微多普勒信号为例,对本文所提分离和参数估计方法进行仿真验证.分量1的微动参数:振动频率、振动幅度和初始相位分别设为256 Hz,5×10−5m和π/3 rad,信号幅度和相位分别为A1=3,θ1=π/4 rad;分量2对应的微动参数设置为300 Hz,2×10−5m和π/6 rad,信号幅度和相位设为A2=1,θ2=π/5 rad.设信号噪声为零均值高斯白噪声,信噪比已知为20 d B,激光波长λ=1550 nm,采样率为fs=312 kHz. 首先根据3.1节介绍的方法计算信号的奇异值比谱,结果如图5(a)所示.扫描周期点数从n=1001点开始,∆d取0.1,图中只有一个明显的峰值在第2178点,所以由SVR估计的微动频率为fs·[1001+(2178−1)×∆d]−1=256.0105 Hz,定义为fv1.将fv1作为已知量计算,利用改进的似然函数计算Dv1和ρ01的概率密度分布,如图5(b).与图2(a)相比可以看出,对激光微多普勒信号的似然函数进行重新设计后,可以把传统密集多峰的分布形状变为平滑单峰的分布,有利于参数的搜索和算法的收敛.此外还降低了对参数初始化精度的要求,只要设置范围合理即可,不需要提前进行精确计算.图5(c)和图5(d)给出了本文方法和传统方法对激光微动参数进行最大似然估计的收敛结果,图中曲线标注“LF”表示似然函数.对比图中四种方法可以看出利用本文设计的似然函数,结合Gibbs算法具有最高的效率,在本文方法下参数Dv1和ρ01收敛到真值需要的迭代次数最少.而MH方法由于在多参数情况下的更新效率低,所以收敛速度较慢.相比之下,利用传统方法计算激光微动信号的似然函数,由于密集局部峰值的存在,不管利用哪种算法都不能正确估计出微动参数,收敛结果停留在初始值附近的某个极大值处.把估计出的微动参数代入(23)式重构分量1的单位调制信号,再根据(25)式和(26)式计算分量1的真实幅度和相位. 从总的回波信号中减去分量1,按照相同的步骤对剩余分量进行参数估计.剩余分量的SVR如图6(a)所示.图中峰值在第391点处,可求出对应分量2的微动频率为300 Hz.图6(b)为分量2对应微动参数的概率密度分布,剩余信号的概率分布仍然是平滑单峰形状,可以保证分量2参数的正确收敛.图6(c)和图6(d)为分量2微动参数的MCMC估计对比结果,整体结果与图5一致,利用传统的似然函数得到的马氏链被困在初始值附近,而改进的似然函数确保了正确的收敛.此外,与图5对比还可发现分量2估计的马尔可夫链收敛到真值的速度较分量1更快.这是因为分量1参数被精确地估计,从原始信号中移除重构的分量1后,分量2成为剩余信号的主要成分,没有其他信号分量的影响,所以收敛更快. 图5 分量1的微动参数估计结果 (a)奇异值比谱;(b)参数D v1和ρ01的概率密度分布;(c)振动幅度;(d)振动初始相位Fig.5.The estimation results of component 1 in the simulation data:(a)SVR;(b)the PDF of D v1 andρ01;(c)vibration amplitude;(d)vibration initial phase. 图6 分量2的微动参数估计结果 (a)奇异值比谱;(b)参数D v1和ρ01的概率密度分布;(c)振动幅度;(d)振动初始相位Fig.6.The estimation results of component 2 in the simulation data:(a)SVR;(b)the pdf of D v1 andρ01;(c)vibration amplitude;(d)vibration initial phaseξ. 各分量参数估计的具体结果和相对误差如表1所列.表中RE=(ˆψ−ψ)×100%/ψ,表示相对估计误差;γ=|E[sk(n)ˆsk(n)]|·|E[sk(n)]2·E[ˆsk(n)]2|−1/2表示波形相似度,通过对比重构信号ˆsk(n)与实际信号在波形上的相似程度来反映参数估计的准确度,γ越接近1则波形相似度越高,表明参数估计越接近真实值.从表1可以看出,本文方法对目标微动参数估计的相对误差都在10−5量级,具有较高的精度. 为定量分析本文方法的参数估计精度,计算不同信噪比下的估计均方误差MSE=并与CRB对比.令信噪比变化范围为−5—35 dB,每隔5 d B进行100次蒙特卡罗实验计算MSE,对比结果如图7. 从图7中可以看出,由于两个分量中参数值的差异导致各信噪比下的CRB也存在差异.但随着信噪比的增加,分量1和分量2的微动参数估计MSE都逐渐接近各自的克拉美罗界,说明本文基于MCMC和重新定义的似然函数来实现微动参数的最大似然估计具有最优的估计性能.此外,仔细对比可发现,各信噪比下分量2中参数的估计误差都略大于分量1的,这是因为对分量2的估计依赖于分量1的结果,会存在一定误差传递的干扰. 表1 参数估计结果Table 1.Parameter estimation result. 图7 微动参数估计均方误差与克拉美罗界对比 (a)分量1参数估计性能;(b)分量2参数估计性能Fig.7.Comparison of MSE and CRB:(a)Parameters of component 1;(b)parameters of component 2. 利用实验数据估计目标微动参数来验证算法有效性,实验设置如图8. 实验结构为全光纤相干激光探测结构,采用波长1550 nm连续波激光器,输出功率40 mW,线宽小于0.1 kHz.激光通过90/10的保偏光纤分束器,9%一路作为信号光,经过光纤扩束系统后照射到两个目标上;另一路经过可调衰减器,作为本振光.接收端采用口径为80 mm的透射式望远镜接收两个目标的散射光信号,回波光和本振光接入平衡探测器,然后由A/D采集卡采集.用振膜扬声器和电驱动音叉模拟微动目标,振动频率分别设为300和256 Hz,振幅在微米量级,振动初始相位由截取信号的时刻决定.实验信号的时域波形与时频分布如图9. 图8 实验结构 (a)系统框图;(b)实物图Fig.8.Experiment system:(a)Structure diagram;(b)experiment setup. 图9 实验信号 (a)归一化时域波形;(b)STFT时频分布Fig.9.Experiment data:(a)Normalized time-domain waveforms;(b)STFT time-frequency distribution. 从图9(a)中可以看出目标振动微多普勒效应对信号的调制效应使两个分量的混合信号在时域上出现了周期性,该周期与目标振动周期一致,所以具备利用SVR谱来估计目标振动频率的条件.图9(b)为混合信号的时频分布,两个分量的微多普勒特征在时频域相互交叠,这一现象将导致传统的信号分离和估计方法失效,体现了研究SCMC时频交叠信号处理方法的必要性.首先利用传统逆Radon变换对时频图进行处理,估计各分量微动参数,作为对比.逆Radon变换估计结果如图10所示. 从图10的逆Radon变换结果可以看出,基于时频分布的参数估计只能把微动参数的估计定位到一个大致区域,并不精确到具体值,这难以保证估计精度.而且,逆Radon定位的参数区域大小严重依赖于时频分布的分辨率,会存在严重的误差传递影响.下面用本文方法对实验数据进行处理,验证算法的有效性.参数估计结果如图11和图12所示. 从图11(a)奇异值比谱中除了得到各分量的振动周期外,还可以得到最高峰和次高峰值比SVR1/SVR2=1.5098,根据图1给出的关系可以得到对应分量的幅值比约为2.1,代入(17)式计算得η=0.815,由此得到的概率分布是理想的平滑单峰形状,如图11(b)所示,可以保证算法快速准确的收敛.利用MCMC方法实现对参数Dv1和ρ01的最大似然估计,结果如图11(c)和图11(d),Markov链迅速得到了收敛,表明锁定了信号真实的参数,整个参数最大估计过程不到1 s,具备实时处理能力.从探测信号中去除分量1,继续对剩余信号进行估计.分量2的周期在图12(a)中有明显的峰值,但SVR谱中除了分量2的主峰值还有分量1的残留分量,这是由于实验中驱动源自身的不稳定和目标对驱动响应不稳定使实验目标对实际振动模拟不理想造成的.实验中的这些不确定性相当于给信号增加了频率噪声,会影响参数估计的精度.但从图12(b)的概率分布形状以及图12(c)和图12(d)的收敛情况看,这并不会影响该方法对参数2中分量的估计效果.算法对实验数据处理得到的收敛效果与仿真分析一致,验证了算法的有效性.为定量分析对比参数估计的准确度,这里用波形相似度γ来验证参数估计的准确度,并与传统非参数化方法进行对比,结果如表2. 图10 逆Radon变换估计结果 (a)分量1参数;(b)分量2参数Fig.10.Results of iRadon:(a)Parameters of component 1;(b)parameters of component 2. 图11 实验数据分量1的微动参数估计结果 (a)奇异值比谱;(b)参数D v1和ρ01的概率密度分布;(c)振动幅度;(d)振动初始相位Fig.11.The estimation results of component 1 in the experiment data:(a)SVR;(b)the PDF of D v1 andρ01;(c)vibration amplitude;(d)vibration initial phase. 图12 实验数据分量2的微动参数估计结果 (a)奇异值比谱;(b)参数D v1和ρ01的概率密度分布;(c)振动幅度;(d)振动初始相位Fig.12.The estimation results of component 2 in the experiment data:(a)SVR;(b)the PDF of D v1 andρ01;(c)vibration amplitude;(d)vibration initial phase. 表2 重构信号波形相似度Table 2.Waveform similarity comparison. 从表2可以看出,利用最大似然估计得到的微动参数重构波形,其相似度达到0.9以上,远高于基于传统时频分布的逆Radon变换重构波形的相似度,验证了参数估计的准确性.说明本文所提方法更有利于实现对微动参数的精确估计,这为基于微动特征的目标分类和精细识别奠定了基础. 本文针对激光微多普勒探测中存在时频域交叠的单通道多分量混合信号,提出了基于最大似然框架的参数估计方法和基于信号重构的分离方法.激光对微弱振动微多普勒效应的探测有不可替代的优势,但激光微多普勒效应对信号的深度调制也使传统似然函数性质发生了本质变化.对此文中给出了适合激光信号的似然函数计算方法,可以得到理想的概率密度分布形式,同时降低了初始化要求,提高了MLE的抗噪能力.通过改进奇异值比谱方法精细扫描混合信号的周期性,得到目标微动频率信息.利用均值似然函数给出了MLE的解析表达,并在求得微动频率的基础上利用MCMC方法实现对剩余微动参数的最大似然估计,解决了复杂的高维积分的问题.利用估计的微动参数重构单位调制信号,估计了信号的幅度和初始相位,通过对各个微动分量所包含参数的分离估计,实现了对单通道混合信号中微动特征参量的精确提取.仿真和实验数据的处理结果验证了所提算法的有效性.该方法可实现对单通道混合微多普勒信号参数的精确估计,为基于微动参数的目标分类和识别以及对目标振动精细成像提供了可能. [1]Chen V C 2006 IEEE Trans.Aerosp.Electron.Syst.42 2 [2]Jiang Y 2014 Ph.D.Dissertation(Xi’an:Xidian University)(in Chinese)[姜悦 2014博士学位论文 (西安:西安电子科技大学)] [3]Yang J,Liu C,Wang Y 2015 IEEE Trans.Geosci.Remote Sens.53 920 [4]Chen V C 2011 The Micro-Doppler Eff ect in Radar(Fitchburg:Artech House)pp15–17 [5]Wang T,Tong C M,Li X M 2015 Acta Phys.Sin.64 058401(in Chinese)[王童,童创明,李西敏2015物理学报64 058401] [6]Hong L,Dai F,Wang X 2016 IEEE Geosci.Remote Sens.Lett.13 1349 [7]Zhu H,Zhang S N,Zhao H C 2014 Acta Phys.Sin.63 058401(in Chinese)[朱航,张淑宁,赵惠昌2014物理学报63 058401] [8]Simeunovic M,Popovic-Bugarin V,Djurovic I 2017 IEEE Trans.Aerosp.Electron.Syst.53 1273 [9]Tan R,Lim H S,Smits A B 2016 IEEE Region 10 Conference,TENCON,2016 p730 [10]Chen G F 2014 Ph.D.Dissertation(Xi’an:Xidian University)(in Chinese)[陈广锋 2014博士学位论文 (西安:西安电子科技大学)] [11]Zhao M M,Zhang Q,Luo Y 2017 IEEE Geosci.Remote Sens.Lett.14 174 [12]Yang Q,Deng B,Wang H 2014 EURASIP J.Wirel.Comm.1 61 [13]Huo K,You P,Jiang W D 2010 Jounal of Electronics&Information Technology 32 355(in Chinese)[霍凯,游鹏,姜卫东2010电子与信息学报32 355] [14]Deng D H,Zhang Q,Luo Y 2013 Acta Electronica Sinica 41 2339(in Chinese)[邓冬虎,张群,罗迎 2013电子学报41 2339] [15]Zhu H,Zhang S N,Zhao H C 2015 Digital Signal Process.40 224 [16]Sun Z G,Chen J,Cao X 2016 J.Syst.Engin.Electron.10 1973 [17]Zhang S N,Zhao H C,Xiong G,Guo C Y 2014 Acta Phys.Sin.63 158401(in Chinese)[张淑宁,赵惠昌,熊刚,郭长勇2014物理学报 63 158401] [18]Sharafi nezhad S R,Alizadeh H,Eshghi M 2014 Elect.Eng.22nd Iranian Conference on IEEE Iran,2014 p1673 [19]Wang Y,Wu X,Li W 2016 Neurocomputing 171 48 [20]Yuan B,Chen Z,Xu S 2014 IEEE Trans.Geosci.Remote Sens.52 1285 [21]Setlur P,Fauzia A,Moeness A 2011 IET Signal Proc.5 194 [22]Ye Z F 2009 Statistical Signal Processing(Hefei:China University of Science and Technology Press)pp241–246(in Chinese)[叶中付 2009统计信号处理(合肥:中国科学技术大学出版社)第241–246页] [23]Guo L R,Hu Y H,Wang Y P 2016 Proceedings of the SPIE,Photonics Asia Beijng,China,October 11–14,2016 p21 [24]Hu Y,Guo L,Dong X 2016 Ubiquitous Positioning,Indoor Navigation and Location Based Services(UPINLBS)Fourth Int.Conf.IEEE Shanghai,China,November 2–4,2016 p264 [25]Hou Z F,Yang J,Zhang X 2011 Journal Wuhan University of Technology 1 142(in Chinese)[侯者非,杨杰,张雪2011武汉理工大学学报 1 142] [26]Kay S M 2006 Fundamentals of Statistical Signal Processing:Estimation Theory(Prentice Hall PTR:Upper Saddle River)pp142–150 [27]Li j,Zhao Y J,Li D H 2014 Acta Phys.Sin.63 130701(in Chinese)[李晶,赵拥军,李冬海 2014物理学报 63 130701] [28]Guo L R,Hu Y H,Wang Y P 2017 Infrared and Laser Engineering 46 17(in Chinese)[郭力仁,胡以华,王云鹏2017红外与激光工程 46 17]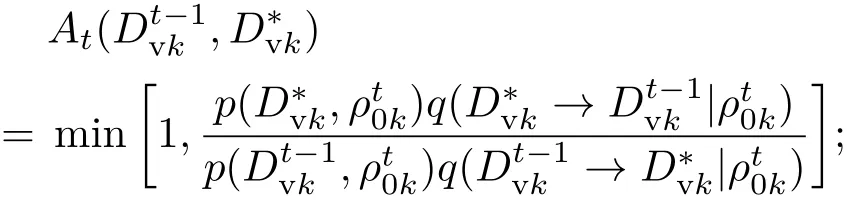
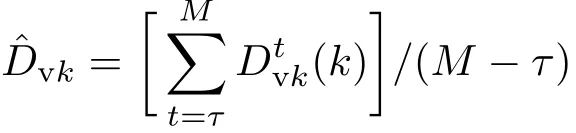
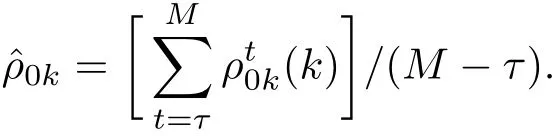
3.3 信号幅度和初相的估计
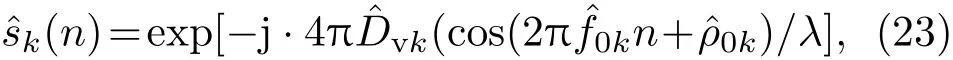

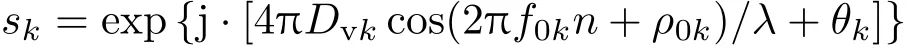
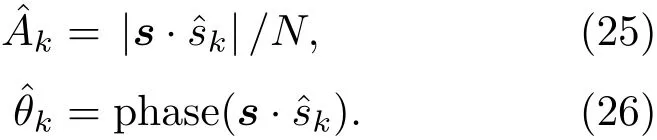
3.4 激光M D信号参数估计的克拉美罗界
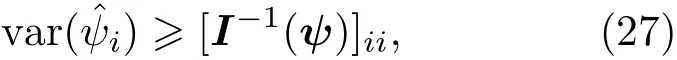
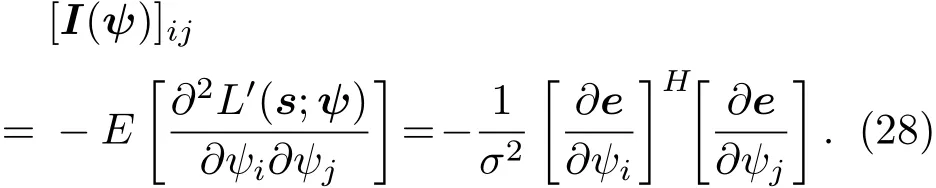
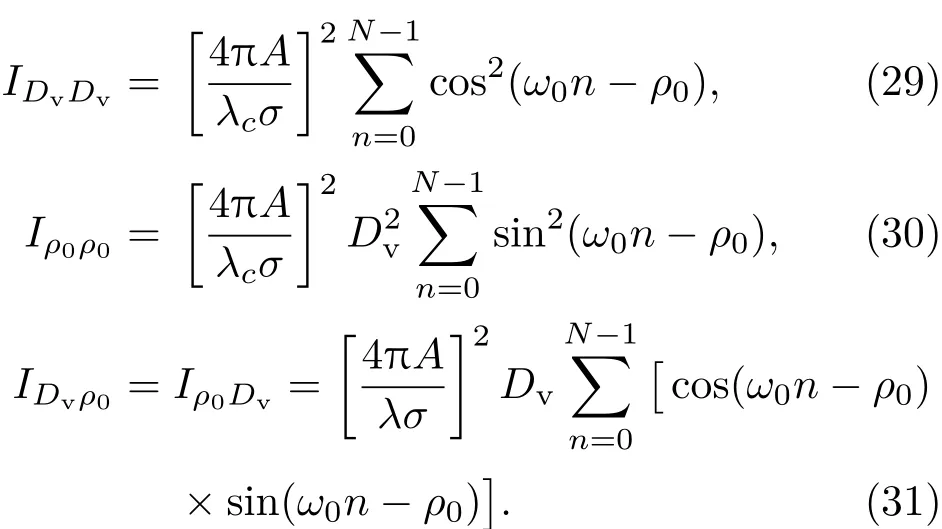
4 仿真分析和实验验证
4.1 仿真结果与分析
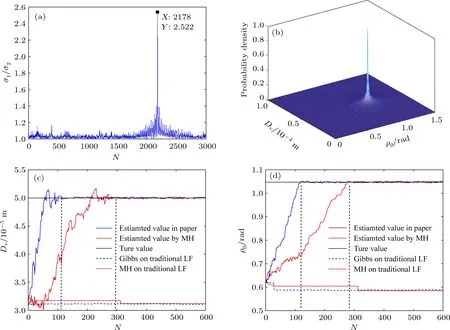
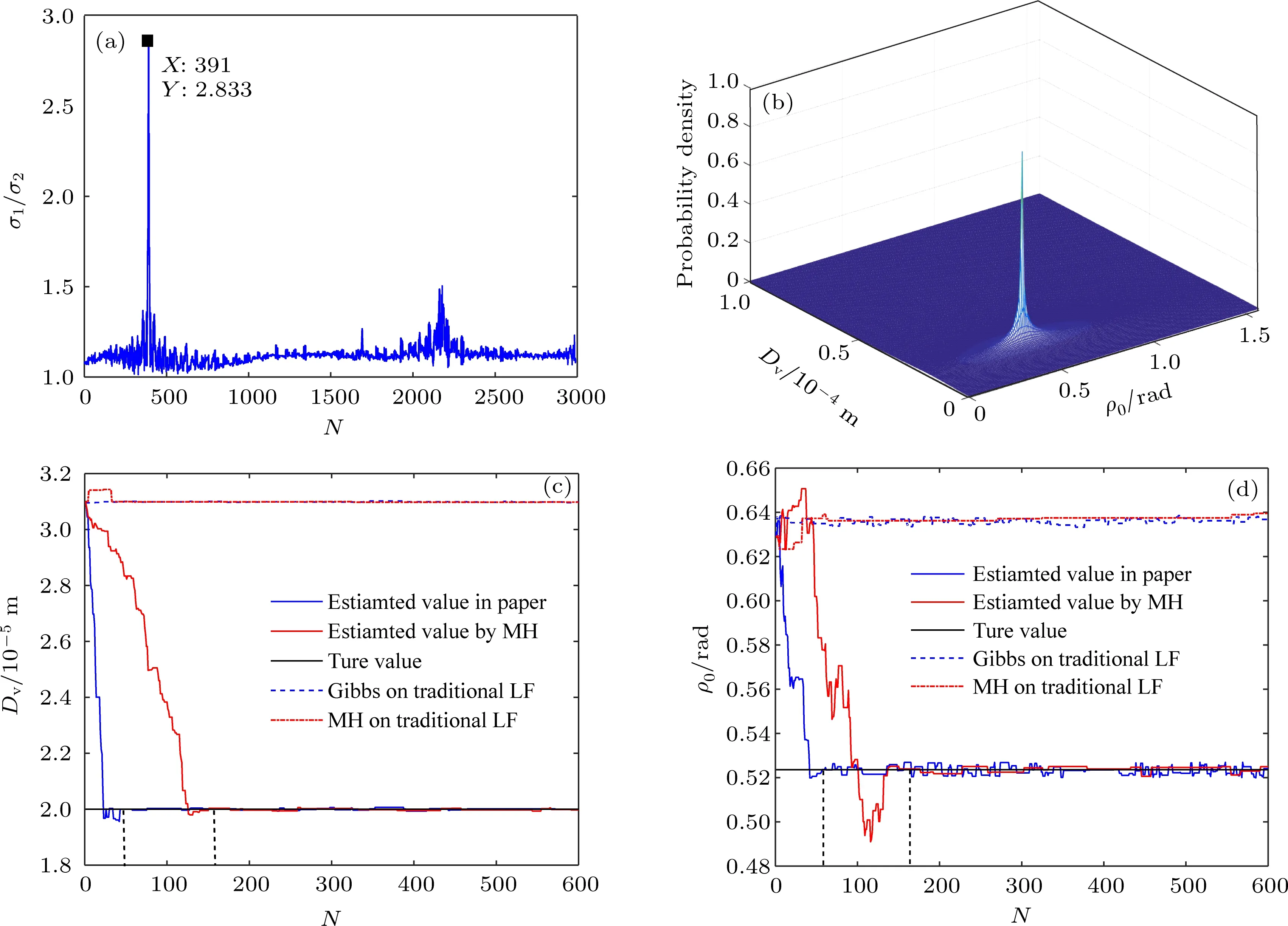

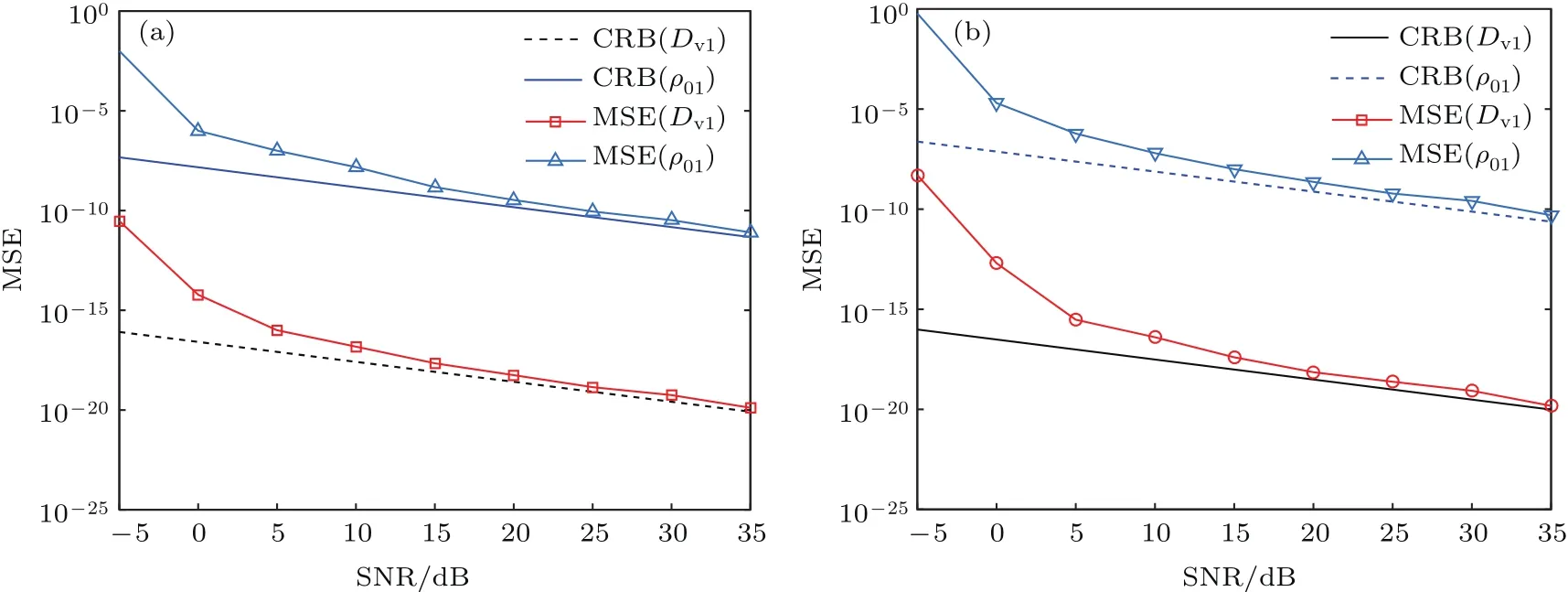
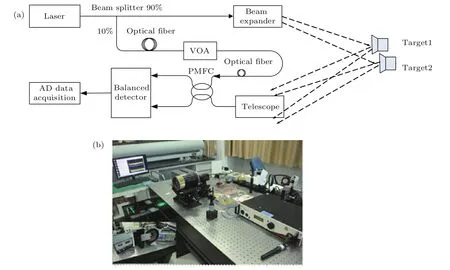
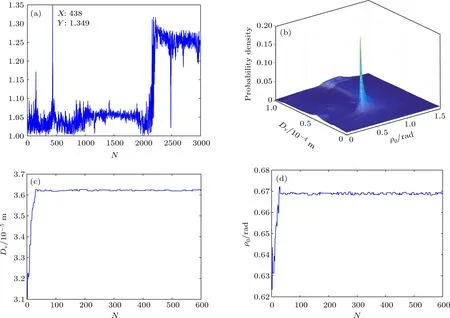
4.2 实验验证与对比



5 结 论
