质子碰撞电离过程中程函近似效应的理论研究∗

2018-06-19陈展斌马堃

物理学报 2018年11期

陈展斌马堃

1 引言

离子-原子碰撞是原子与分子物理领域的基本过程之一,广泛存在于天体物理和实验等离子体环境中,对该过程的深入研究不仅可以揭示详细的原子内部结构以及散射过程中的动力学信息,还可以为天体物理、等离子物理、核聚变、团簇物理、医学、材料、加速器等提供实验依据,具有重要的应用价值[1−9].相对于电子散射过程[10−15],离子-原子碰撞提供了更为丰富的物理图像,因此,在过去的几十年中,引起了许多理论和实验物理学家的关注.在实验方面,早期的离子原子碰撞主要局限于H,He2+离子和He等简单原子的直接电离过程和单电子俘获过程,而在离子与多电子靶碰撞过程中的电子俘获和电子丢失等总截面的测量方面,受限于多个反应通道,从所测数据上很难清晰反映通道之间的分支比例以及获取更为精细的碰撞动力学机制.20世纪80年代中期,随着离子原子碰撞实验技术的发展,克服了以前实验方法的不足,在确定散射离子电荷态的同时,采用的飞行时间技术也确定了反冲离子的电荷态,这样根据碰撞反应过程中电荷守恒规律就可以明确地鉴别出各个反应通道.近年来,随着离子源和加速器技术的发展以及对不同的反应过程中的所有产物实现完全测量和碰撞产物成像技术的进步,人们可以从复杂反应通道中揭示更加深刻的物理机制.

实验中得到大量数据的同时也有力地推动了理论工作的展开,一些新颖的理论模型应运而生,如一阶玻恩近似方法、经典轨道蒙特卡罗方法、半经典近似理论、扭曲波模型、通过解耦合方程来得到所需波函数的密耦合理论等.此外,为了解决一阶近似方法在某些场合下失效的问题(如入射离子电荷过大,或入射粒子与电子间的距离太小),20世纪90年代,人们发展了连续扭曲波方法(CDW)及连续扭曲波程函初态近似方法(CDW-EIS),并将之运用于粒子碰撞电离研究[1,16−20].其基本思路是:当碰撞粒子各方彼此足够分离,电子的渐近行为可以较精确地描述,即初态电子处于靶的束缚态和入射粒子的连续态;末态电子同时处于靶与入射粒子电场的连续态.CDW-EIS理论则是在CDW理论的基础上将初态波函数加上程函扭曲相因子,更好地考虑了双中心效应及一些有特点的碰撞效应.由于其具有非常好的适用性、灵活性、简洁性,为人们细致地探索初、末通道中相互作用与动力学问题提供了便利条件,因此,在离子碰撞领域得到了广泛的应用.但是,据我们所知,相关的实验和理论文献中大多只研究了结构较简单的壳层和电子少的靶原子,对于多电子原子的研究相对较少.此外,对于模型差异的报道及初通道程函近似效应对截面的影响的研究也相对匮乏.

本文分别利用CDW和CDW-EIS方法对质子(H+)与复杂氖原子1s,2s,2p壳层的碰撞电离过程进行了理论研究,计算得到了质子与氖原子碰撞电离的总截面、单重微分散射截面(SDCS)和二重微分散射截面(DDCS),比较了不同模型的结果,分析了截面曲线的细致结构,研究了初态程函近似效应对各截面的影响,并探讨了该体系碰撞电离过程所涉及的各种电离机制.

2 理论方法

关于CDW和CDW-EIS理论,在文献[1,16—20]中给出了较为详尽的描述,这里只做一般介绍.在CDW理论方法中,初、末态波函数分别表述为[1,16]:

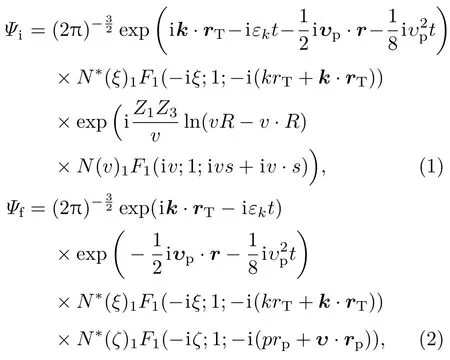
其中R=rT−rp,rT和rp分别为实验室坐标系中电子相对于靶核和入射粒子的位矢;r=(rT+rp)/2;ξ=ZT/k;ζ=Zp/p;ZT和Zp分别为靶和入射粒子的有效核电荷数;k为出射电子相对于靶核的动量;p=k−υp为出射电子相对于入射粒子的动量;εk=k2/2为出射电子相对于靶核的动能;− iξ;1;−i(kr+k ·r)和T1F1− iζ;1;−i(prp+p ·rp)是合流超几何函数,分别表示靶核和入射粒子对出射电子的库仑扭曲;N(a)=exp(πa/2)Γ(1− i a)是库仑态密度因子.当入射粒子与靶的作用使得靶中电子从一个量子态Ψi跃迁到另一个量子态Ψf时,其跃迁概率可以表示为

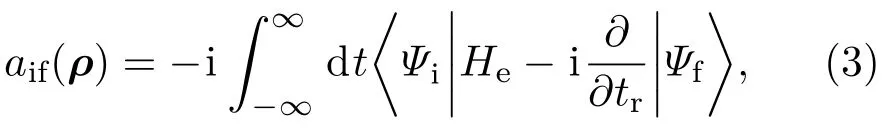
其中ρ为碰撞参数,其方向与入射粒子的速度υp垂直;Ψi表示体系总的初态波函数;Ψf表示体系总的末态波函数.CDW-EIS理论是用初态程函近似替代CDW理论的扭曲库仑因子,即初态波函数表示为[1,16−20]

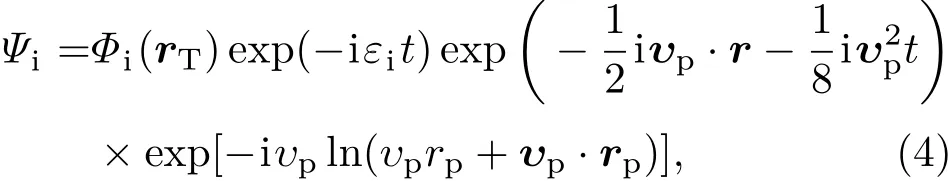
其中υp为入射粒子相对于靶核的速度;Φi(rT)为活跃电子以靶核为中心的电子束缚态波函数,在具体计算中采用Roothaan-Hatree-Fock(RHF)波函数;εi为束缚能;最后一项exp[−iυpln(υprp+ υp·r)]为程函扭曲因子.

体系哈密顿量可以写为

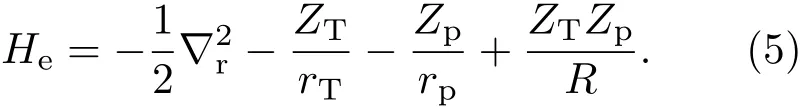
利用上述公式可得电离过程的三重微分截面(TDCS)为[1,16]

对动量积分,得到DDCS为

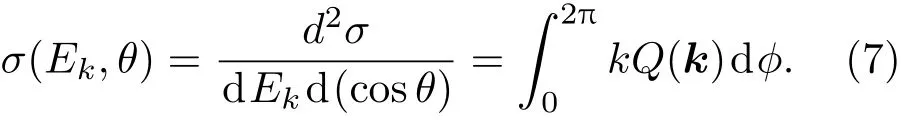
再对能量或者角度积分,可得到极角的SDCS和能量的单重微分截面,分别表示为

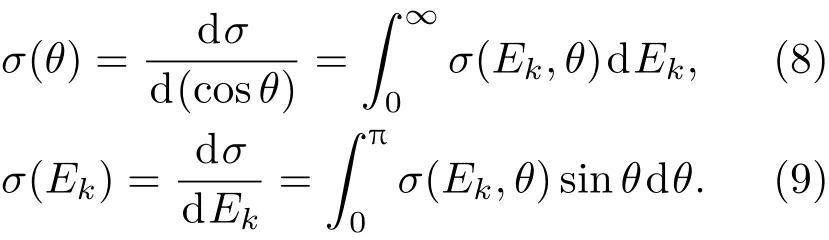
进一步,完成极化或者能量的积分,最终可以得到质子碰撞的总散射截面

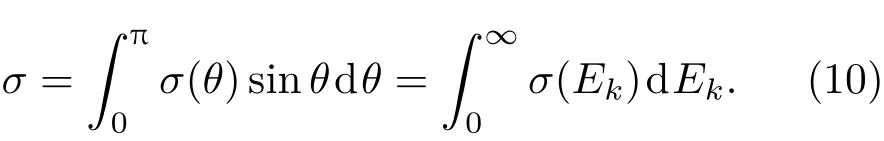
3 结果与讨论

基于(7)—(9)式,分别采用CDW和CDW-EIS模型对Ne原子1s,2s和2p壳层的质子碰撞电离截面、SDCS和DDCS进行了详细的计算,并分析了所得曲线的细致结构.

3.1 总截面

图1给出了用CDW-EIS模型计算的质子碰撞电离氖原子1s,2s,2p壳层截面及总截面随入射能量的变化关系,相应计算结果分别记为1s,2s,2p和total.作为比较,图中同时给出了总电离截面(圆点)及2s壳层电离截面(三角)的实验数据.如图1所示,随着入射质子能量的增加,各曲线的总散射截面快速增加到峰值,然后缓慢减小;且内、外壳层对应的峰值位置向着入射能量减小的方向移动,如1s电离的总散射截面的峰值位置出现在300 keV/u附近,2s电离的总散射截面的峰值位置出现在100 keV/u,2p电离的总散射截面的峰值位置出现在80 keV/u.这主要是由于当入射粒子的速度接近靶内束缚电子的速度时,靶内电子比较容易受到入射粒子的作用而被俘获到入射粒子的连续态,从而形成峰的结构;由于氖原子复杂的结构,内壳层1s电子受到靶核的束缚作用相对较大,内层电子要比外壳层2s或2p电子挣脱靶核的束缚更加困难,因此2s,2p壳层电子的总散射截面要远远大于1s壳层电子的散射截面.此外,注意到,在低能入射区域,电离1s与2s壳层之间的截面相差较大,随着入射能量的增大,1s壳层截面与2s壳层之间差异逐渐减小,幅度逐渐接近.同时,可以看到,目前理论结果与实验数据之间符合得非常好,除了在低入射能量区域总截面与实验数据存在部分差异之外,目前计算的2s截面和总截面结构及幅度与实验数据基本重合.

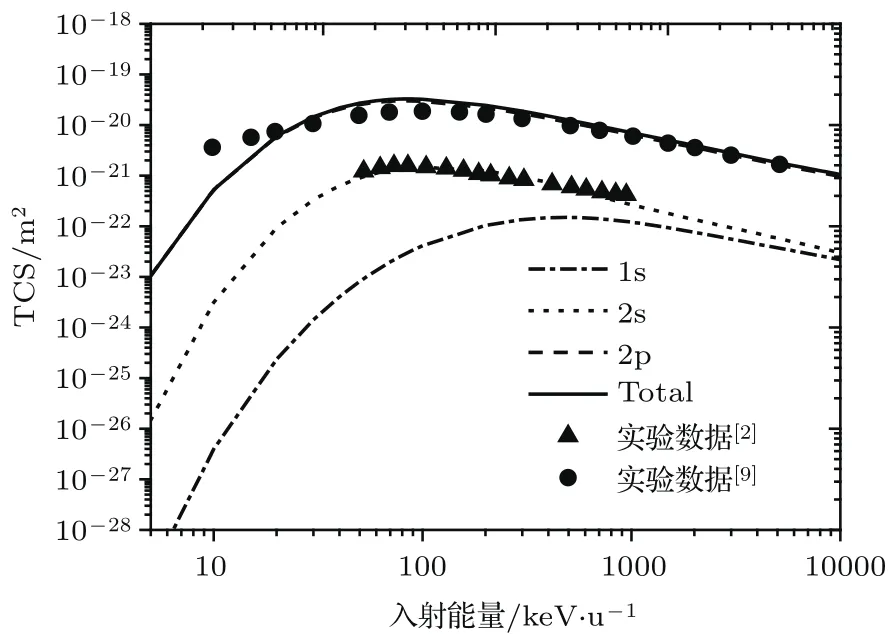
图1 CDW-EIS模型计算的随入射质子能量变化的总散射截面Fig.1.Present CDW-EIS cross sections as a function of the incident energy.

3.2 微分散射截面

离子-原子碰撞过程中,电子出射机制非常复杂,而微分截面则是揭示电子出射机制的一个重要的物理量,探讨微分截面特征对于加深对碰撞机制的理解有着重要作用.图2(a)和图2(b)给出了入射粒子能量为600 keV/u时,分别利用CDW和CDW-EIS两种模型计算得到的电离不同壳层的DDCS随出射电子能量的变化关系.图2(a)中出射电子的散射角θ=0◦,图2(b)中出射电子的散射角θ=6◦.遗憾的是,在该几何条件下,没有找到相关实验的数据做比较.从图2可以看出,各壳层的截面显现明显的峰结构,其中,在岀射电子的低能区域,电子能量靠近能量零点的峰为软碰撞电离(SC)峰.随后出现的与电子被俘获到连续态机制有关的第一个明显的峰为入射粒子连续态(ECC)峰,该峰的位置位于靶内束缚电子的速度与入射粒子的速度匹配时,在目前的几何条件下,氖原子中各分壳层电子均能被入射粒子俘获到连续态而产生ECC峰.且其位置T满足T=meυ2p/2关系,例如图2(a)中ECC锋的位置为出射电子能量327 eV处,与目前的计算结果符合得较好.在高能区的末端,产生的峰主要来自二体相遇碰撞电离(BE),此时二者之间发生大的动量转移,出射电子获得很高的能量,形成了BE峰.根据能量和动量守恒,当出射电子的散射角θ=0◦时,出射电子获得的能量满足EBE=4T−2I关系,式中I为靶中电子的电离能,可以看到目前的理论BE峰位置与计算结果符合得也较好.此外,比较不同壳层随岀射电子能量的变化可以看到,在目前能量条件下,对于碰撞电离最内1s壳层没有出现二体碰撞时产生的BE峰,这是由于1s壳层电子比2s,2p壳层电子受到原子核的束缚强,因此,对应的截面值小且部分峰结构没有显现.这一规律与总截面呈现的规律一样.如图2(b)所示,当出射电子散射角θ=6◦时,出射方向与入射粒子的速度方向不一致,可以看到,各分壳层截面中的ECC峰的强度迅速减小而逐渐消失.在高能区的末端,产生的峰主要来自二体相遇碰撞电离,此时二者之间发生大的动量转移,出射电子获得很高的能量,形成了BE峰.同样,根据能量和动量守恒,可以看到目前的理论BE峰位置与计算结果符合得也较好.与总截面的规律类似,1s壳层电子比2s,2p壳层电子受到原子核的束缚强,因此,对应的截面值小且部分峰结构也没有显现.此外,通过对CDW和CDW-EIS两种模型计算结果的比较可以看到,在目前的几何条件下,两种模型所得结果之间差异较小,极小的差异仅出现在电离1s壳层岀射时电子低能区域上,对于电离2s,2p壳层各截面随岀射电子能量的变化基本重合.

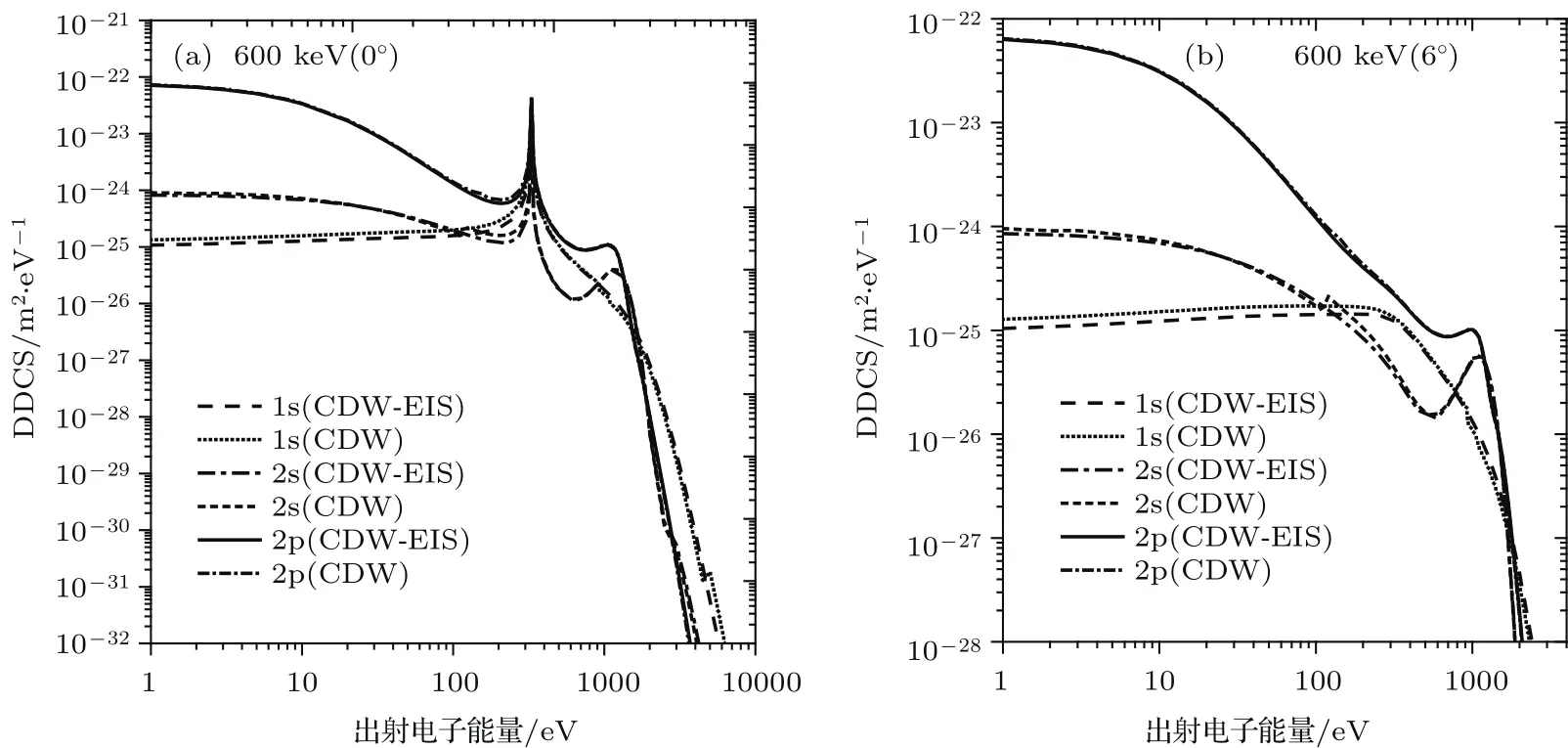
图2 分壳层的DDCS随出射电子能量的变化关系 (a)θ=0◦;(b)θ=6◦Fig.2.DDCS of each shell as a function ofthe ionized electron energy:(a)θ =0◦;(b)θ =6◦.

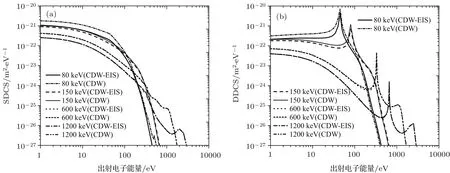
图3 不同入射能量时电离2p壳层的SDCS和DDCS随出射电子能量变化的关系 (a)SDCS;(b)DDCSFig.3.SDCS and DDCS of 2p shell as a function ofthe ionized electron for diff erent incident energy:(a)SDCS;(b)DDCS.

图3 (a)和图3(b)给出了出射电子散射角θ=0◦,入射粒子能量分别为80,120,600,1200 keV/u时,质子入射碰撞电离氖原子2p壳层的SDCS和DDCS随出射电子能量的变化关系.如图3所示,2p外壳层SDCS随着出射电子能量的增加首先变化平缓,随后急剧下降.按照前面对于能量区域的划分[1],可以看到,随着入射粒子能量的增加,SC的能量区域增加,ECC电离的能量区域和BE电离区域依次向高能方向平移增加,这个区域变长;而强度大小依次减小,减小速度变快.因此,从SDCS形成上可以推断出,出射电子在低能区以软电离机制为主,而随着能量的增大,对于高能入射粒子,软碰撞电离机制所占的区域变长,比重变大.此外,比较图3中的结果还可以看到,两种模型结果之间的差异主要在于低能质子碰撞,随着入射质子能量的增大,模型之间的差异逐渐减少,以致于各曲线之间基本重合.与此同时,在入射能量固定的情况下,模型之间的差异主要出现在出射电子能量较低的区域,随着出射电子能量的增大,差异逐渐消失.如图3(b)所示,对于DDCS,随着入射质子能量的增加,SC峰、ECC峰和BE峰依然存在,但3个峰值的大小逐渐减小,ECC峰和BE峰位置逐渐增大.这是由于入射能量增加时,对峰形成的条件不再较好地满足,因此各峰的强度都迅速变小;此外由公式EBE=4T−2I可以看到ECC峰和BE峰的位置向高能发生了平移,SC峰的分布区域增宽,TCEE区域[1]相对增大.同样,比较两种理论模型的结果可以看到,两种模型之间的差异主要在于低能质子碰撞,随着入射质子能量的增大,模型之间的差异逐渐减少,在高能入射时两种模型之间的曲线基本重合.当入射能量固定时,模型之间的差异主要出现在出射电子能量较低的区域,随着出射电子能量的增大,差异也逐渐消失.

3.3 初态程函近似效应

当电子被俘获到入射粒子连续态时,对应着双中心效应,虽然CDW可以很好地描述低能区的ECC电离,但由于CDW模型下初态波函数没有归一化,因此在中能区所得到的结果往往会比实验值偏高.而CDW-EIS模型则是初态波函数的基础上乘以一个程函扭曲相因子,不改变末态波函数,这样就可以很好地考虑双中心效应,弥补CDW初态函数不归一的缺点.下面将进一步探讨CDW及CDW-EIS模型之间的差异,揭示初态程函效应对各壳层截面的影响.图4(a)和图4(b)给出了入射粒质子能量为20 keV/u时,SDCS与DDCS随出射电子能量的变化关系.如图4所示,初态程函近似效应对于内壳层的影响比外壳层大,主要表现在幅度上,而对峰的位置影响较小.

为了进一步了解初态程函近似对氖原子不同壳层SDCS和DDCS的影响,图5给出了程函效应对SDCS和DDCS影响的相对值(CDW−CDW-EIS)/CDW.从图5可以看出,对于SDCS,CDW-EIS的结果普遍比CDW的结果大,约为2倍;对于DDCS,CDW的结果比CDW-EIS的结果大很多,在高能区域甚至大4个数量级.程函效应对不同壳层的影响也不相同,例如,无论是SDCS还是DDCS,程函对2p壳层截面的影响几乎与出射电子能量无关;对1s壳层和2s壳层的影响规律基本一致,均随着出射光子能量的增加,出现3个分段单调区间,即0—1000 eV,1000—2000 eV,2000 eV以上,在各区间内均是随着出射电子能量的增加而增加.这是因为多重微分截面携带着大量散射过程的相关信息,同时多重微分截面上的变化趋势所体现出来的特征也更丰富,DDCS多于SDCS,因为后者完成了对前面角度和能量的积分,在图像上已缺少了相关的物理信息.因此,程函近似对DDCS特征上的影响要比对SDCS的影响大得多.

图4 入射粒质子能量为20 keV/u时,分壳层SDCS和DDCS随出射电子能量的变化关系 (a)SDCS;(b)DDCSFig.4.SDCS and DDCS of each shell as a function of ionized electron atan incident energy of 20 keV/u:(a)SDCS;(b)DDCS.

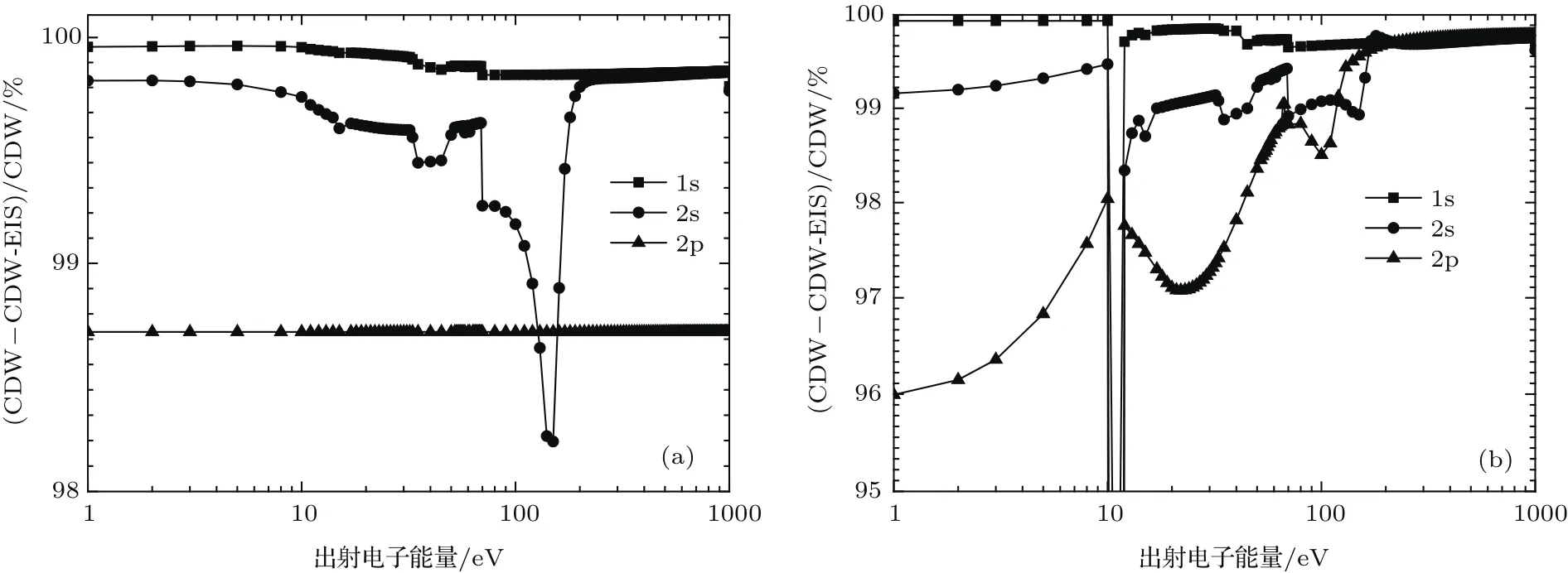
图5 入射粒质子能量为20 keV/u时程函效应对分壳层(a)SDCS,(b)DDCS的影响Fig.5.SDCS(a)and DDCS(b)of each shell as a function of ionized electron at incident energy of 20 keV/u.

4 结论

本文利用CDW和CDW-EIS理论分别计算了质子与氖原子的碰撞电离过程,得到了碰撞电离过程的总散射截面及随出射电离电子能量变化的SDCS和DDCS.所得结果与实验数据进行了比较,分析了截面曲线的细致结构,研究了初态程函近似对截面的影响,并对其内部碰撞电离机制进行了探讨.结果表明,目前的计算结果与实验符合得较好.对于电离氖原子2p壳层,随着入射质子能量增加,SDCS的区域变长、幅度减小,在低能区以软电离为主,而DDCS出现的峰均迅速减小.比较两种理论发现,CDW模型计算的分壳层截面随着电离电子能量的增大,结果较CDW-EIS模型先高后低,在峰分布方面符合得较好.初态程函近似效应对截面的影响随入射能量的增大而逐渐减小,呈现出一定的规律性,在较低能入射时尤为明显.

感谢Mcsherry教授提供的代码,黄炼和王凯博士对论文的修改,以及S.Xue博士给予的建设性意见.

[1]Ning Y,He B,Liu C L,Yan J,Wang J G 2005 Acta Phys.Sin.54 3075(in Chinese)[宁烨，何斌，刘春雷，颜君，王建国2005物理学报54 3075]

[2]Eckhardt M,Schartner K H 1983 Z.Phys.A:Hadrons Nucl.312 321

[3]Janev R K,Kato T,Wang J G 2000 Phys.Plasma 7 4364

[4]Miraglia J E,Gravielle M S 2010 Phys.Rev.A 81 042709

[5]Tong X M,Li J M 1987 Acta Phys.Sin.36 773(in Chinese)[仝晓明，李家明 1987物理学报 36 773]

[6]Zhou X X,Zhang X Z,Chen H S,Dong C Z 1997 Acta Phys.Sin.46 1096(in Chinese)[周效信，张现周，陈宏善，董晨钟1997物理学报46 1096]

[7]Suzuki S,Gulyás L,Shimakura N,Fainstein P D,Shirai T 2000 J.Phys.B 33 3307

[8]Schultz D R,KrstićP S,Reinhold C O 1996 Phys.Scr.T 62 69

[9]Rudd M E,Kim Y K,Madison D H,Gallagher J W 1985 Rev.Mod.Phys.57 965

[10]Chen Z B,Dong C Z,Xie L Y,Jiang J 2014 Phys.Rev.A 90 012703

[11]Chen Z B,Dong C Z,Jiang J 2014 Phys.Rev.A 90 022715