论PowerPoint在全等三角形判定教学中的应用
2018-06-19四川省岳池县大佛初级中学校
四川省岳池县大佛初级中学校 王 茜
当代中国,随着国家对教育的投入增多,义务教育均衡发展的推行,学校硬件和软件设施(尤其是农村地区)逐步完善,教师使用多媒体辅助教学常态化。现在亟需解决的是:激发学生学习的热情同时,于单位教学时间内,学生熟练应用本节课的知识解决实际问题,丰富已有的知识体系结构。
一、全等三角形判定的相关概念
定义:能够完全重合的两个三角形叫做全等三角形,重合的顶点叫做对应顶点,
重合边叫做对应边,重合的角叫做对应角。
性质:全等三角形的对应边相等,全等三角形的对应角相等
判定:1.三边分别相等的两个三角形全等(简写“边边边”或“SSS”)
2.两边和它们的夹角分别相等的两个三角形全等(简写“边角边”或“SAS”)
3.两角和它们的夹边分别相等的两个三角形全等(简写“角边角”或“ASA”)
4.两角分别相等且其中一组等角的对边相等的两个三角形全等(简写“角角边”或“AAS”)
5.斜边和一条直角边分别相等的两个直角三角形全等(简写“斜边、直角边”或“HL”)
二、基于PowerPoint的全等三角形判定的教学应用
PowerPoint,我们一般习惯简写成PPT,能够制作出集文字、图形、图像、声音以及视频剪辑等多功能的的演示文稿, 在一组图文并茂的画面中以多种形式呈现,由于其操作原理简单易学,且使用方便,一般情况下,教师在课堂教学中更青睐于用PPT辅助教学。
PPT辅助教学具有以下特点:1.界面简洁新颖,交互性强,有利于解决教学中的重难点。2.画面生动形象,往往将静态教学动起来,学生更有积极性。3.扩大教师的教学面,增加学生的知识量。它帮助教师为学生进行自主建构提供资源并创设任务情境,多维度的使学生全面发展,增强了教学效果。
在进行全等三角形的判定的教学时,从复习全等三角形的性质导入新课:“三边分别相等且三个角分别相等的两个三角形全等”,在此基础上,创设情景,帮助学生自主探究如何判定两个三角形全等。
首先,让学生探究如何精简条件以及至少需要多少个条件,一开始,学生可能无法完全自主探究,这时老师的引导就很重要,为了使学生对全等三角形是否全等有直观印象,我们可以用PPT将图形动态地呈现出来,直接面向全体学生模拟两个三角形能否完全重合。
通过老师给出的提示,学生可分小组探究,依次总结出:一个条件相等或两个条件相等均不能保证三角形全等。在此过程中,学生既可以培养探究精神,也可以树立团结的意识,更增强了学习数学的乐趣。
探究满足三个条件的情况下,两个三角形是否全等,我们有四种情况:1.三个角分别相等;2.三条边分别相等;3.两条边及一个角分别相等;4.两个角及一条边分别相等。
以探究两条边及一个角分别相等的两个三角形是否全等为例,在老师的指导下,结合PPT的使用,学生依靠自己努力对此判定进行证明,得出结论。
两条边及一个角分别相等的情况除了边角边(SAS),还存在另一种可能,也就是满足两边和其中一条边的对角分别相等的两个三角形是否全等,可以留给学生课后思考、课后探究这也是一个不错的选择,也体现了新课标的教学要求。
有了前面两节课的经验,两条角及一个边分别相等的两个三角形是否全的问题,学生处理起来也得心应手。

图2-9 问题导入
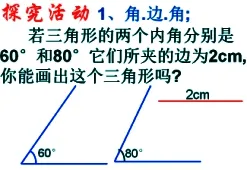
图2-10 探究两角及其夹边相等判定两个三角形全等
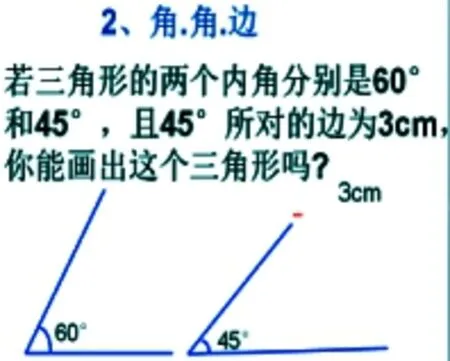
图2-11 探究两个角及其一角对边相等判定两个三角形全等
这节课的知识点在老师和学生的共同努力下,我们可以获得:

图2-12 得出结论:ASA、AAS
最后,老师可以启发学生思考一个问题:△ABC中,∠C =90°直角边是BC、AC,斜边是AB,这样的三角形是直角三角形,直角△ABC记作 Rt△ABC,前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
例如:两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?(答:全等,根据AAS ,这两个直角三角形全等。)
又或者:两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?(答:全等,根据ASA ,这两个直角三角形全等。)
在多年的教学实践中,我们必须承认PPT教学确实给课堂教学带来了更多的可能性,但我们依然不能忽视传统教学的可靠性,在不能利用PPT辅助教学完成教学任务的情况下,应当更有耐心的为学生传道、授业、解惑。我们必须谨记:在利用现代信息技术为课堂教学“减负”的同时,作为一名教师,永远不能将自己的职责——教书育人“减负”。
