压缩感知在无线传感网的节能应用综述
2018-06-19林德钰郭新明
林德钰,郭新明
(1.西安电子科技大学 计算机学院,陕西 西安 710071;2.咸阳师范学院 信息工程学院,陕西 咸阳712000)
无线传感器网络(Wireless Sensor Networks,WSNs)是由大量传感器节点密集铺设以自组织形式构成的网络系统。因传感器节点成本低廉,铺设简单而被广泛应用在数据获取、环境监测、灾难救援等场景中。[1]传感器节点大多数采用电池供电,且大多数传感器网络节点数量庞大,给各个传感器节点更换电池或者补充能量显得不切实际。因此,能量受限是WSNs不容忽视的瓶颈之一。[2-3]近年来,围绕如何提高能量效率、延长网络生命期等关键问题,出现了一系列研究成果。其中包括:分簇路由策略[2-3]、移动Sink节点策略[4-5]、拓扑控制技术[6-7]以及数据聚合技术[8]等。同时,由于传感器网络大多数情况下采取了密集铺设的形式,这导致数据采集过程中来源于连续区域内的数据具有一定的冗余性,此即感知数据的空间相关性;另一方面,传感器节点连续进行数据感知,造成数据在临近时段内也存在冗余——数据的时间相关性。因此,合理地消除数据的时空相关性可以进一步节约传感器能耗,进而延长网络生命期。
压缩感知(Compressed Sensing,CS)理论是近些年出现的,是一种利用信号稀疏性、数理统计理论以及最优化理论进行信号处理与描述的新的框架[9-11]。压缩感知理论首先由Doboho D、Candes E以及Baraniuk R等人首先提出,并且作出了奠基性成果,提出了压缩感知的理论框架。在传统的信号获取中,奈奎斯特采样定理是信号获取的理论基础,即为了完整地获取原始信号,采样频率至少必须为原始信号的最高频率的两倍以上。CS理论的提出颠覆了奈奎斯特采样定理对采样频率的要求,即针对原始状态具有稀疏性的信号或者在一定的变换基下具有稀疏性的信号可以在降低采样频率的情况下高精度地还原原始信号。CS理论使得采样频率依靠信号本身的特性而不再依赖于信号带宽。并且,有别于常规的数据压缩技术,CS可以将采样与压缩同步进行,压缩采样过程中只需要简单的乘法与加法操作,将复杂的数据恢复操作留待汇聚节点进行。显然,这种特点适用于传感器节点能量、处理能力受限而Sink节点处理能力以及能量相对无限的传感器网络。
1 压缩感知理论框架
压缩感知理论框架包括三个主要构件:信号稀疏性、有限等距性质(RIP)以及信号恢复算法。其中,信号稀疏性是前提,有限等距性质为压缩感知的充分条件,信号恢复算法是基于压缩感知数据采集的关键。
1.1 信号稀疏性
假设传感器网络中有N个节点,每个节点获知的数据表示为x i(1≤i≤N),则WSNs中所采集的所有节点获得原始数据可以表示为X=x(x1,x2,...,x n)。假如存在某个稀疏变换基Ψ使得下式成立时,信号X称为K-稀疏信号。
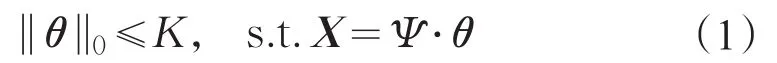
成立,其中,矩阵θ为信号X的稀疏系数矩阵,||θ||0表示向量θ中所有非零元素的个数。
1.2 有限等距性质
为进行稀疏信号的压缩感知,需构建相应的观测矩阵Φ,则采集信号可表示为y=ΦX,其中X=Ψθ。观测矩阵Φ为M×N矩阵,通过合理设计观测矩阵,最终获得观测信号y为M×1矩阵,由于M≪N,因此实现了对信号的压缩感知。通过观测矩阵y精确恢复原始信号X的充分条件是,观测矩阵Φ满足有限等距性质(Restricted Isometry Property,RIP)。即对于任意信号X,存在一个任意小的非负常数ε满足下列不等式

此时,则称观测矩阵Φ满足集合大小为K,参数为ε有限等距性质。对于观测矩阵而言,其行数M代表所需采集的测量值数目。一般而言,测量值数目M与稀疏度K需要满足如下关系:

1.3 原始信号重构
根据测量值y重构为原始信号X,且已知观测矩阵Φ的前提下,为了实现最小采样率,可将原始信号的恢复过程规划成如下的l0优化问题:

从而获得原始信号的近似解如下式(5)所示:

事实证明:上述l0范数的求解为NP-Hard问题。因为需要穷举X的所有可能组合,当X的维数变大时,无法直接求得其最优解。因此,Donoho提出,在观测矩阵Φ满足RIP性质时,可用l1范数的最优解来近似代替l0范数的最优解[12]。因此,原始信号X的重构问题转化为如下凸优化问题:

从而求得原始信号近似解为:

2 压缩感知在传感器网络节能策略中的应用
2.1 压缩感知数据收集框架
Luo等人首先提出了基于CS的大规模无线传感网的数据收集框架(Compressive Data Gatheriing,CDG)[13]。在CDG框架中,对如图1所示的两种传输模型进行了理论分析。图1a)示的传统数据传输模式下,假设传感器网络中铺设有N个节点,每个节点Si(1≤i≤N)产生的数据记为d i,显然节点Si所需要传输的数据量为i(i-1)2。N个节点所需要传输的数据量为n(n+1)(4n-1)12,即为Θ(n3)。然而,采用CDG框架之后(如图1b所示),每个节点传输的数据量为M,因此,整个网络的数据传输负载为Θ(MN)。由于M< 近年来,不少学者开始采用分簇机制与压缩感知相结合的数据收集机制[14-22]。文献[14]中Lan提出一种基于CS的分簇算法——Compressibility-based Clustering Algorithm(CBCA)。在CBCA中,网络拓扑先由网状拓扑转换成逻辑链状拓扑,再根据WSNs中存在的空间相关性进行分簇以最小化平均压缩比。文中采用了类两种数据传输模式:Raw Data Gathering(RDG)以及 Compressive Data Gathering(CDG)。设计了阈值机制以确定数据的传输模式,并根据压缩比Compression Rate(CR)动态地确定传输模式以及分簇尺寸。实验证明:CBCA算法可以在压缩率为40%条件下实现小于5%的相对误差还原率。Li等人在文献[15]中提出一种Unbalanced Expander Graph based Compressive Data gathering(UEGCD)算法,从理论上证明了对于一个含有N c个簇的WSNs,当M=Ο(klogN/k)以及t=Ο(Nc/kq)同时成立时,M×N阶稀疏感知矩阵对应于一个(k,ε)非平衡扩展图的邻接矩阵。通过仿真实验证明UEGCD可以节约27.8%的能量。Zhao等人在文献[16]中指出,常用于信号稀疏变换的离散余弦变换基并不能很好地稀疏化真实信号,因其会削弱CS数据压缩的优势,在此基础之上提出了Treelet-based Clustered Compressive Data Aggregation(T-CCDA)算法。利用数据之间的相关特性提出了基于Treelet的稀疏变换矩阵,由此提出了一种新型的分簇路由算法。仿真结果表明:由于T-CCDA采用了将T-CDA与分簇相结合的策略,相比未采用分簇的T-CDA策略可以在通信开销上提高30%的性能。文献[17]针对信号存在的可压缩性以及信号的非均匀产生特性提出一种非均匀压缩感知算法。定义了两种不同的采样分布模型,即均匀伯努利分布模型以及非均匀伯努利分布模型。通过扩展的CS理论,非均匀CS框架可以高概率地重构异构采样信号。Xie等人在文献[18]提出一种基于分簇的混合CS数据收集算法,将整个传感网划分成簇。簇内的成员节点按照传统数据收集方式将数据传输至簇头节点,簇头节点按照数据压缩的方式将数据传输至Sink节点。最后构建了关于分簇尺寸与传输量之间关系的分析模型并且在此基础上得出可最小化传输量的最优分簇数目。文章指出,在含有N个传感器的WSNs中,若最优化的分簇尺寸为N*c,则可得出最优分簇数目为[N N*c]。仿真实验表明,与传统分簇策略相比,采用基于CS的分簇策略时数据传输量可以减少60%。文献[19]提出了一种测量矩阵优化算法MMOA,使用弥散小波变换矩阵DWTM作为压缩感知的稀疏基矩阵。在此基础上提出了一种基于CS以及路由拓扑的优化数据融合树ODAT。文献[20]将压缩感知与分簇算法PEGASIS[23]相结合进行数据获取。采用PEGASIS策略进行分簇,同时采用CS进行簇内数据压缩,因此可以同时实现减少通信能耗和以及均匀化能耗的目的。文献[21]提出一种时空数据收集模型,主要包括两个组件:能量自适应数据汇集算法A-HDACS以及Matrix Completion(MC)。具体来说,单个时隙内采用随机节点子集的方式来减少数据空间相关性;同时在时间段内,通过转换成Matrix Completion减少数据时间相关性从而减少能耗。文献[22]提出一种带有移动Sink的合作式压缩感知分簇节能算法——DSM-NbC。该算法中,移动Sink智能地向节点密集区域移动,由于大部分传感器节点只需要单跳地传输数据,因而可以显著地节约能量。同时,为了避免稀疏区域节点因为等待移动Sink节点而造成缓冲区溢出,采用了按需分簇技术。基于合作式的分簇策略可以进一步减少网络通信开销以及降低计算复杂性。 除了上述将CS理论与分簇路由算法相结合的节能策略之外,近年来还涌现了一系列关于压缩感知在无线传感器网络中节能应用的其他策略[24-34]。文献[24]提出一种基于邻居协助的压缩感知方案——NACS用于高能效地收集时空关联数据。每一个感知阶段,传感器节点将原始感知数据传输给随机选出的邻居节点,邻居节点进行基于CS的数据压缩并后将压缩过的数据发送至Sink节点。文献[25]从CS与随机图论结合的角度出发,提出了一种随机行走数据数据收集算法。从理论上证明了当采取m=Ο(klog(n k))次随机独立行走,并且每次行走步长为t=Ο(n k)时,可以采用l1优化算法来精确重构k稀疏信号。Zheng等人在其前期工作[25]的基础上进一步提出综合采用随机行走以及核方法的移动CDG方案[26]。文献[26]证明了基于核函数的稀疏基矩阵满足RIP性质,同时在该方案中,移动数据收集器使用m=Ο(klog(n k))次测量就可以实现数据精确重构。与文献[25]相比,步长值仅为t=Ο(klog(n k))。Liu等人在文献[27]中提出一种基于CS高保真度且适用于任意拓扑结构的网络节能数据收集策略。并且通过真实数据集以及合成数据集证实了该算法的有效性。此外,Yang等人在其工作中采用了分布式数据存储DDS结合CS以及网络编码技术来高能效地进行传感网的数据收集——CNCDS[28]。实验结果表明,CNCDS可以在传输数目Nttot、接收数目Nrtot以及数据恢复平均均方误差分别减少55%、74%及76%。同时针提出了自适应CNCDS方案,与常规CNCDS相比,传输数目Nttot、接收数目Nr tot可以分别减少63%和32%。此外,Quer等人在文献[30]中使用主成分分析法获得实际信号的时空关联特性,结合CS提出一种可在线恢复原始信号的无线传感器数据收集策略。由此定义了一种结合CS以及主成分分析PCA的数据收集框架SCoRe1。Chen等人在文献[29]中针对收集一维信号的传感器网络提出了一种基于CS的数据收集框架。在此框架中,采用反馈机制实现自适应控制采样速率。采用SCI指标在线监测数据恢复误差,实现在一定的数据恢复精度内最大限度地减少传输能耗。同时伴随着CS技术而产生的节能数据收集策略还有基于分布式压缩感知及预测的随机谣传路由[31];CS与数据驴相结合的节能数据收集策略[32];基于树的节能压缩感知数据收集策略[33]以及采用群稀疏的压缩感知数据收集策略[34]。 文献[35-37]对基于CS的传感网数据收集策略性能进行了研究。Karakus等人[35]给出了关于WSNs数据获取、计算以及通信能耗的定量模型。并将该定量模型应用到一个混合整数规划中,将基于CS的数据采集策略DACS与两种传统数据收集方式DANP以及DATC进行对比,实验表明在获取信号高度稀疏(如k N<0.10)以及传感器节点铺设密度较低时(如Rnet≤150 m ,ς=50),DACS策略可以显著地延长网络生命期。Zheng等人[36]从网内通信开销的角度评价了基于CS的传感网的性能。将CS的稀疏矩阵的计算过程规划为随机几何网络的网内计算问题,着眼于减小计算复杂性的角度来进行协议的设计和性能分析。提出一种带有最优更新速率的基于树的计算协议,并且给出了能耗以及网络延迟的特性关系。在此基础上提出一种旨在降低能耗和较少网络时延的块状计算协议,同时也设计了一种增强鲁棒性的基于谣传路由的协议。Zheng等人[37]针对稀疏分布的无线传感器网络分别在采用单Sink和多Sink的情况下,使用CS技术时的网络容量和延迟。文章指出,在采用单Sink的情况下,其容量和延迟分别为,其中W、M分别表示链路带宽和压缩感知测量值数量。对于采用nd个Sink节点、每个Sink节点平均收集随机选取的ns个传感器节点的数据时,所能获得的网络容量和网络延迟分别为和 本文首先简要分析了无线传感器网络存在的瓶颈——能量受限问题,概括了压缩感知理论。压缩感知理论可以让传感器网络在进行数据收集时摆脱传统奈奎斯特采样定理所需要的采样频率要求,并且有别于传统数据融合技术,可以实现数据采集与数据压缩同时进行。复杂的数据恢复留待具有较强处理能力以及相对无限能量预算的Sink节点处理。因此CS理论恰好适用于无线传感器网络数据收集。对压缩感知理论的三个基本构件进行了简单阐述,紧接着对压缩感知在无线传感器网络节能策略上的应用进行了综述。近年来CS在无线传感器网络节能方向的应用主要体现在四个方面:基于压缩感知的数据收集框架(CDG),与分簇路由策略相结合的压缩感知数据收集策略,其他应用压缩感知的节能数据收集策略以及基于CS的节能策略的性能分析。结合上述研究现状的分析,对未来基于CS的无线传感器网络数据收集可在如下方向做一定的研究: (1)目前基于CS的节能策略大多基于一个假设,即网络中不存在或者不考虑丢包率。然而,现实的WSNs中一定的丢包率是不可避免的。因此,未来的研究中,应该对存在丢包的WSNs作进一步研究。在满足一定的丢包率以及满足一定数据恢复精度的前提下,设计最大化能量效率的CS节能策略。 (2)目前现有关于基于分簇的CS节能策略基本大多假设簇头节点之间的通信采用SPT来构建路由树。尽管根据SPT算法,可以保证簇头节点在进行数据转发时使得能量最小化,然而这并不利于能量的均衡。为了使得WSNs网络生命期足够长,需要尽可能优化数据传输的能量效率。能量效率包括两个方面:能耗最小化以及能耗均衡。因此,未来的CS节能策略需要同时考虑最大化节约能量的同时使得能耗尽可能均衡。 (3)现有的研究成果大多聚焦在一维信息获取上,所谓一维数据获取是指所有传感器节点都是同构的。如都是温度传感器或者湿度、风速等单一物理量传感器。显然,在实际应用中,例如在农作物生存条件的监控应用中需要对多种物理指标进行监测。因此,如何将CS应用到多维信息的获取是未来一个值得进行深入研究的课题。 [1]FRANCESCO M D,Das S K,ANASTASI G.Data collection in wireless sensor networks with mobile elements∶A survey[J].ACM Transactions on Sensor Networks,2011,8(1):1-31. [2]LIN D Y,WANG Q,LIN D Q,et al.An energy-efficient clustering routing protocol based on evolutionary game theory in wireless sensor networks[J].International Journal of Distributed Sensor Networks,2015(223):1-12. [3]LIN D Y,WANG Q.A game theory based energy efficient clustering routing protocol for WSNs[J].Wireless Networks,2017,23(4):1101-1111. [4]BASAGNIS,CAROSIA,MELACHRIOUDISE,et al.Controlled sink mobility for prolonging wireless sensor networks lifetime[J].Wireless Networks,2007,14(6):831-858. [5]林德钰,王泉,刘伎昭.无线传感网的移动与静态sink相结合的节能策略[J].哈尔滨工业大学学报,2016,48(11):162-168. [6]LIN D Y,WANG Q,LIU J Z.An energy efficient sink deployment scheme aiming at extending the lifespan for wireless sensor networks[J].International Journal of Future Generation Communication and Networking,2016,9(8):77-86. [7]WU X B,CHEN G H,SAJALl K.Avoiding energy holes in wireless sensor networks with nonuniform node distribution[J].IEEE Transactions on Parallel and Distributed Systems,2008,19(5):710-720. [8]杨军,张德运,张云翼,等.基于分簇的无线传感器网络数据汇集传送协议[J].软件学报,2010,21(5):1127-1137. [9]DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306. [10]BARANIUK RG.Compressive sensing[J].IEEESignal Processing Magazine,2007,24(4):118-121. [11]CANDES E J.Compressive sampling[C]//Proceedings on the International Congress of Mathematicians.Madrid,Spain,the European Mathematical Society,2006:1433-1452. [12]DONOLO D L,ELAD M,TEMLYAKOV V N.Stable recovery of spare overcomplete representations in the presence of noise[J].IEEE Transactions on Information Theory,2006,52(1):6-18. [13]LUO C,WU F,SUN J,et al.Compressive data gathering for large-scale wireless sensor networks[J].International Conference on Mobile Computing and Networking,2009,14(1):145-156. [14]LAN K,WEIM Z.A compressibility-based clustering algorithm for hierarchical compressive data gathering[J].IEEE Sensors Journal,2017,17(8):2550-2560. [15]LI X L,TAO X F,MAO G X.Unbalanced expander based compressive data gathering in clustered wireless sensor networks[J].IEEEAccess,2017,5:7553-7566. [16]ZHAO C,ZHANGW X,YANGY,et al.Treelet-based clus-tered compressive data aggregation for wireless sensor networks[J].IEEETransactionson Vehicular Technology,2015,64(9):4257-4267. [17]SHEN Y R,HU W,RANA R,et al.Nonuniform compressive sensing for heterogeneous wireless sensor networks[J].IEEESensors Journal,2013,13(6):2120-2126. [18]XIE R T,JIA X H.Transaction-efficient clustering method for wireless sensor networks using compressive sensing[J].IEEE Transactions on Parallel and Distributed Systems,2014,25(3):806-814. [19]YAN W J,DONG Y F,ZHANG S Q,et al.An optimal CDG framework for energy efficient WSNs[J].Chinese Journal of Electronics,2017,26(1):138-144. [20]XIE D F,ZHOU Q W,LIU JP,et al.A chain-based data gathering protocol under compressive sensing framework for wireless sensor networks[C]//Proceedings of the 2013 International Conference on Computational and Information Sciences,IEEESociety,2013:1479-1482. [21]XU X,RASHIDA,ASHFAQ K.Spatio-temporal hierarchical data aggregation using compressivesensing(ST-HDACS)[C]//Proceedings of the 2015 International Conference on Distributed Computing in Sensor Systems,Fortaleza,IEEE,2015:91-97. [22]BEHZAD M,GE Y.Performance optimization in wireless sensor networks∶a novel collaborative compressed sensing approach[C]//Proceedings of the IEEE 31stInternational Conference on Advanced Information Networking and Applications,Taipei,2017:749-756. [23]LINDSEY S,RAGHAVENDRA C S.PEGASIS∶power-efficient gathering in sensor information systems[C]//Proceedings of the Aerospace Conference, Big Sky, 2002:3-1125-3-1130. [24]QUAN L,XIAO S,XUE X,et al.Neighbor-aided spatial-temporal compressive data gathering in wireless sensor networks[J].IEEE Communications Letters,2016,20(3):578-581. [25]ZHENG H F,YANG F,TIAN X H,et al.Data gathering with compressive sensing in wireless sensor networks∶a random walk based approach[J].IEEE Transactions on Parallel and Distributed Systems,2015,26(1):35-44. [26]ZHENGH F,GUOWZ,XIONGN X.Akernel-based compressive sensing approach for mobile data gathering in wireless sensor network systems[J].IEEE Transactions on Systems,Man and Cybernetics∶Systems,2017(99):1-13. [27]LIU X,LUOJ,Catherine Rosenberg.Compressed data aggregation∶energy-efficient and high-fidelity data collection[J].IEEE/ACM Transactions on Networking,2013,21(6):1722-1735. [28]YANG X J,TAO X F,DUKIEWICZ E,et al.Energy-efficient distributed data storage for wireless sensor networks based on compressived sensing and network coding[J].IEEE Transactions on Wireless Communications,2013,12(10):5087-5099. [29]CHEN W,WASSELL I J.Energy-efficient signal acquisition in wireless sensor networks∶a compressive sensng framework[J].IET Wireless Sensor Systems,2012,2(1):1-8. [30]QUER G,MASIERO R,PILLONETTO G,et al.Sensing,compression,and recovery for WSNs:sparse signal modeling and monitoring framework[J].IEEE Transactions on Wireless Communications,2012,11(10):3447-3461. [31]RABBAT M,HAUPT J,SINGH A,et al.Decentralized compression and predistribution via randomized gossiping[C]//Proceedings of the International Conference on Information Processing in Sensor Networks,Nashville,TN,USA,IEEESociety,2006:51-59. [32]ZHOU SW,ZHONGQ,OU B.Intelligent compressive data gathering using data ferries for wireless sensor networks[C]//Proceedings of the IEEE International Conference on Acoustics,NEW ORLEANS,USA,IEEE Society,2017:6015-6019. [33]NGUYEN M T,TEAGUE K A.Tree-based energy-efficient data gathering in wireless sensor networks deploying compressive sensing[C]//Proceedingsof the Wirelessand Optical Communication Conference,Newark,NJ,USA,IEEE Society,2014:1-6. [34]LIU SD,LIUY,ZHANGY,et al.Compressve datagathering in wireless sensor networks via group sparse regularization[C]//Proceedings of the IEEEICC 2017 Ah-Hoc and Sensor Networking Symposium,Paris,France,IEEE Society,2017:1-5. [35]KARAKUSC,GURBUSA C,TAVLI B.Analysis of energy efficiency of compressive sensing in wireless sensor networks[J].IEEESensors Journal,2013,13(5):1999-2008. [36]ZHENG H F,GUO W Z,FENG X X,et al.Design and analysis of in-network computation protocols with compressive sensing in wireless sensor networks[J].IEEE Access,2017,99(5):11015-11029. [37]ZHENG H F,XIAOSL,WANGX B,et al.Capacity and delay analysis for data gathering with compressive sensing in wireless sensor networks[J].IEEE Transactions on Wireless Communications,2013,12(2):917-927.2.2 与分簇机制相结合的压缩感知数据收集框架
2.3 其他基于CS的节能策略
3 采用CS的WSNs的性能分析
4 总结与展望
