基于罗特曼透镜的多波束比幅测向算法研究
2018-06-19陈佳林丛天孺赵海波
陈佳林,丛天孺,赵海波
(1.海军研究院,上海 200436;2.中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
多波束阵列天线已在多目标跟踪雷达、电子侦察、电子干扰等传统军事领域得到了广泛应用[1],而相比于相控阵波束形成技术,基于罗特曼透镜的波束形成网络因其宽频带、同时多波束与低成本同时兼顾的优点具有独特的优势。与此同时,相比于相控阵天线技术,若设计时体积及波束数量受限,其幅相一致性便难以保证,导致形成的方向图波束一致性较差。当其作为比幅测向的波束形成网络时,保证测向精度的难度就很大。本文以一个六波束罗特曼透镜方向图为例,比较了传统的高斯近似算法、三角近似算法、三波束算法的优劣,并给出了算法具体应用时的技巧。
1 系统组成和原理
基于罗特曼透镜的多波束比幅测向系统由透镜波束形成网络、对数视频放大器(DLVA)幅度检测、多通道采样及角度计算单元组成[2-3]。以六波束比幅测向系统为例,其组成框图如图1、图2所示。
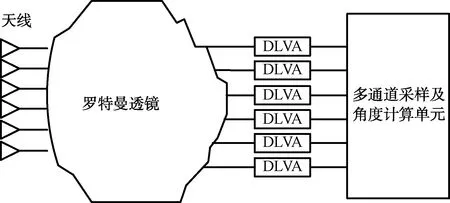
图1 罗特曼透镜六波束测向系统框图

图2 多通道采样及角度计算单元框图
其基本原理是:六元阵天线及罗特曼透镜形成不同指向的6个波束,覆盖±45°范围,透镜波束口将6波束接收信号送至DLVA进行幅度检测,测得的电压值送入多通道采样及角度计算单元计算角度值,送出给后端接收机进行数据融合。
本文的透镜设计工作于S波段,实测其在3 GHz方向图如图3所示。
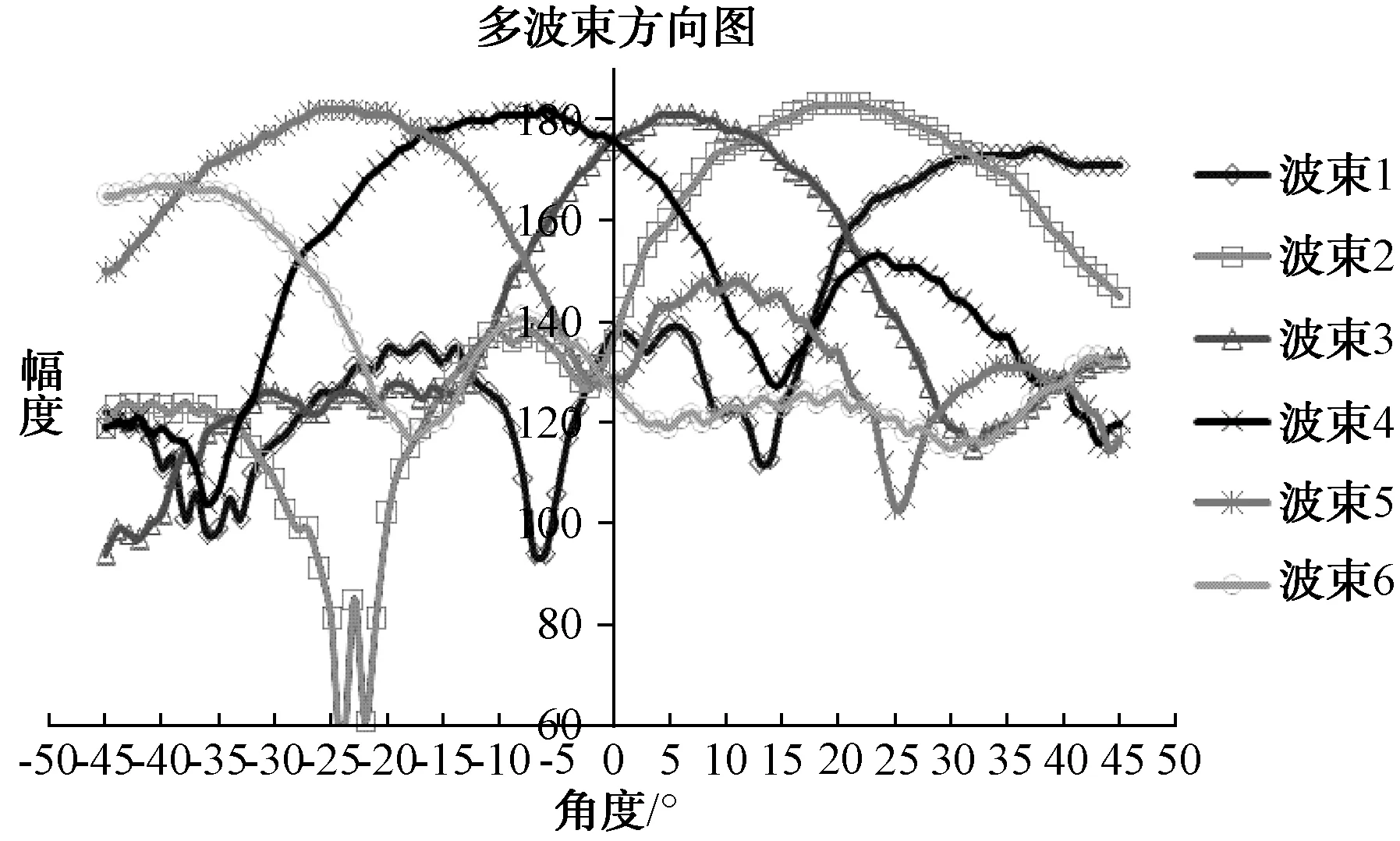
图3 六波束方向图
观察此方向图,其具有如下特点:
(1) 波束幅度一致性差;
(2) 波束宽度一致性差;
(3) 波束指向分布不均匀;
(4) 波束左右对称性差。
显然,要在设计的±45°范围内取得较高的测向精度,需对测向算法进行选择及优化。
2 算法原理介绍
2.1 两波束算法
2.1.1 高斯近似算法
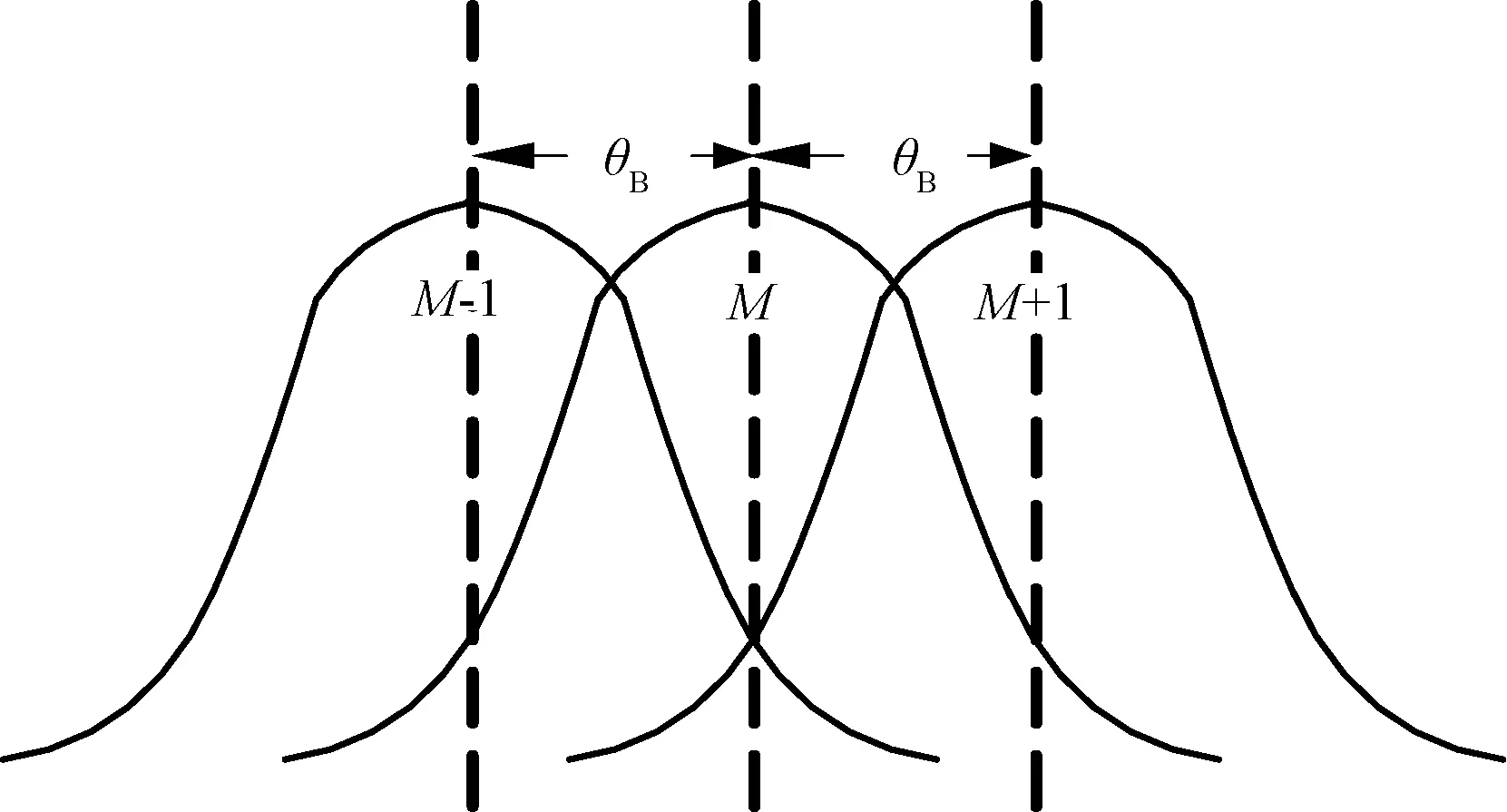
图4 高斯近似算法示意图
设各天线3 dB波束宽度均为θB,信号入射的方位角θ处于第M个天线轴线附近,天线的方向图在偏离轴线±θB的角度范围内通常可以认为是高斯型,高斯近似算法示意图如图4所示。设此时第M个天线顶点幅度为A0,则第M个天线接收信号幅度为:
AM(θ)≈A0e-k(θ-θM)2
(1)
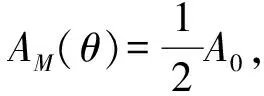
(2)
先将式(1)取对数。此时,需判断第M个波束左右的波束哪个幅度为次大。若第M-1个波束为幅度次大波束,则:
AM-1-A0=-k(θ+θM)2
(3)
AM-A0=-kθ2
(4)
若第M+1个波束为幅度次大波束,则:
AM+1-A0=-k(θ-θM)2
(5)
将式(4)-式(3)得到:
(6)
整理得:
(7)
同理,将式(4)-式(5)得:
(8)
式中:DL=AM-AM-1;DR=AM-A1
因子1/2kθM为高斯近似因子,等效为幅度相差1 dB所对应的角度偏离。
通常,如M-1号波束为次大幅度波束,则取式(7)计算;如M+1号波束为次大幅度波束,则取式(8)计算。
2.1.2 三角近似算法
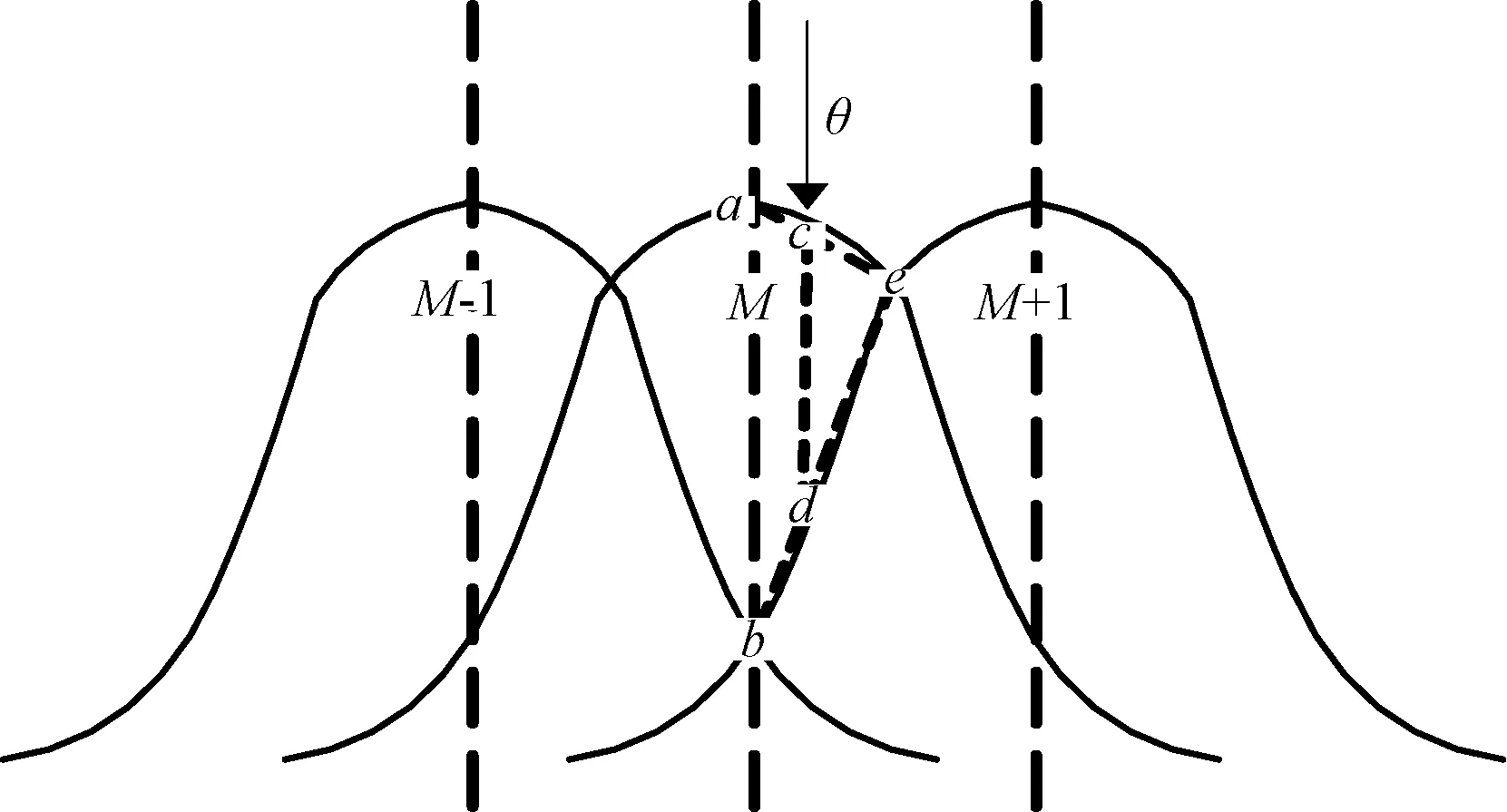
图5 三角近似算法示意图
三角近似算法实现较为简单。三角近似算法示意图如图5所示。设实际信号入射角度为θ,位于第M号与M+1号波束之间。则此时第M号波束接收幅度近似为Ac,第M+1号波束接收幅度近似为Ad。两波束交叉点幅度为Ae。第M号波束中心Aa与第M+1号波束垂线交点为Ab。由近似三角形原理,有:
(9)
求得角度:
(10)
此方法原理简单,利用了与幅度次大波束的波束交叉点参与计算,适用范围较广。
2.2 三波束算法
三波束算法可以看作是上文中高斯近似算法的改良。由于高斯近似算法精度受限于高斯近似因子K的拟合精度,对于波束一致性不好的方向图,由于左右两边波束特性不同,方位数据可能会发生跳变。因此,可同时利用左右波束同时参与计算,以在公式中消除高斯近似因子K。将式(8)和式(7)相加除以2得到两边的平均值:
(11)
但式(11)中仍然含有K,为此再将式(8)和式(7)相减再代入式(11)得:
(12)
实际上,式(12)就是将最大波束分别和左右相邻的一个波束接收的幅度进行计算结果的平均值,而且从式中可以看出计算结果并不包含高斯近似因子K。
综上所述,改善民生的战略价值和着力点已明确,那么靠什么来推动民生问题的解决呢?毛泽东阐述了解决民生问题的基本的动力,这就是一要靠人民,二要靠党和政府制定切合实际的政策。
采用上述方法改善了测向精度,但由于其需要左右两波束同时参与计算,在边缘波束上不适用。
3 算法优化
3.1 方向图幅度校正
显然,针对如图3所示的方向图,利用上述3种方法中无论哪一种均不能达到较高的测向精度,需对方向图进行幅度校正。即找出6个波束中幅度最大波束,比较其余5个波束顶点与此波束顶点的幅度差值,进行幅度补偿,即将方向图“拉平”。进行校正后的方向图如图6所示。
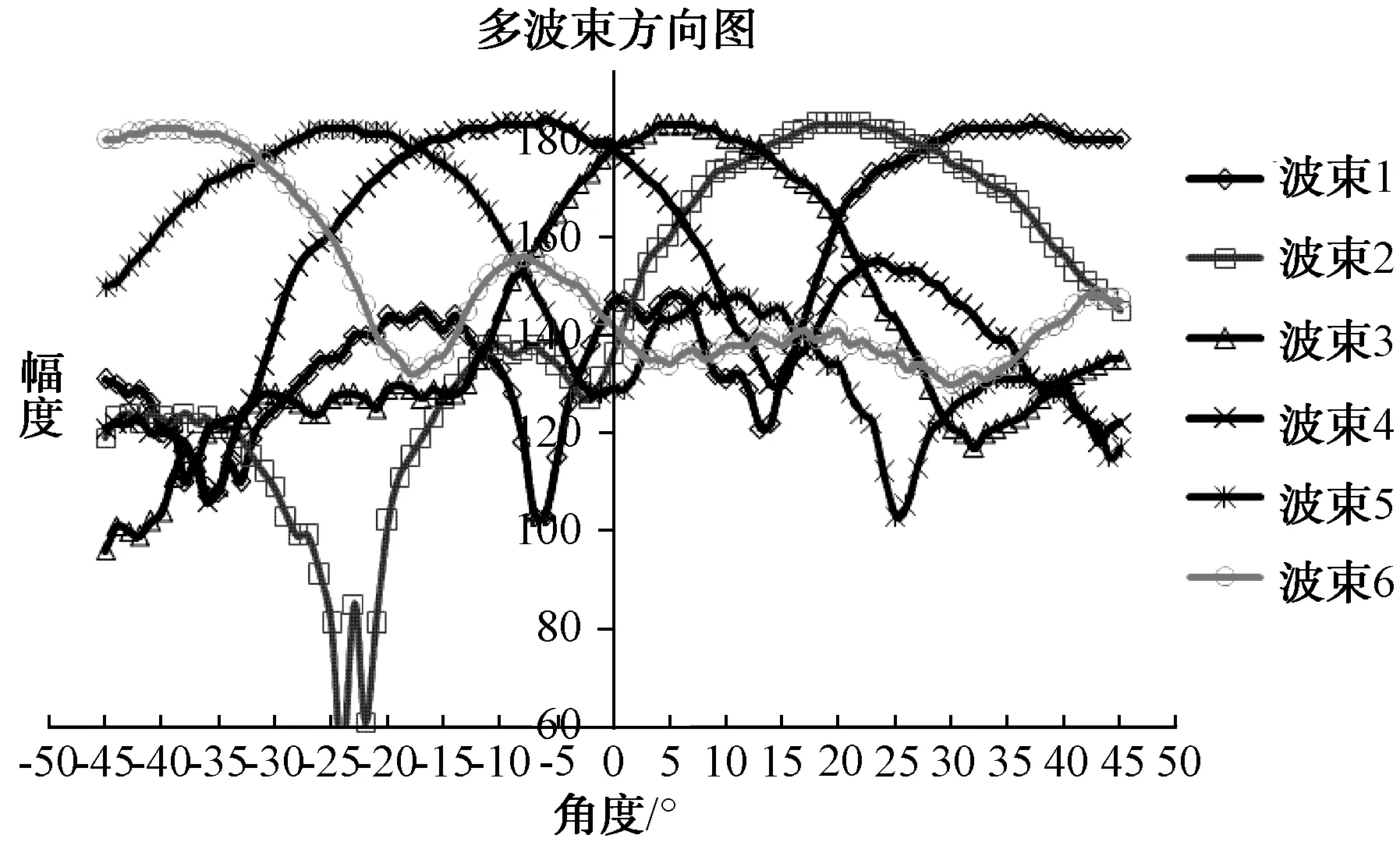
图6 进行幅度校正后的六波束方向图
3.2 边波束梯形近似
显然,上述3种算法在第M+5号波束中心点向外是无法给出测向结果的,而罗特曼透镜又常常由于体积和波束口个数所限无法完全覆盖想要的覆盖范围。此优化方法利用梯形近似原理,对三角近加以优化,使其得以适用于边波束中心点以外,其原理如图7所示。
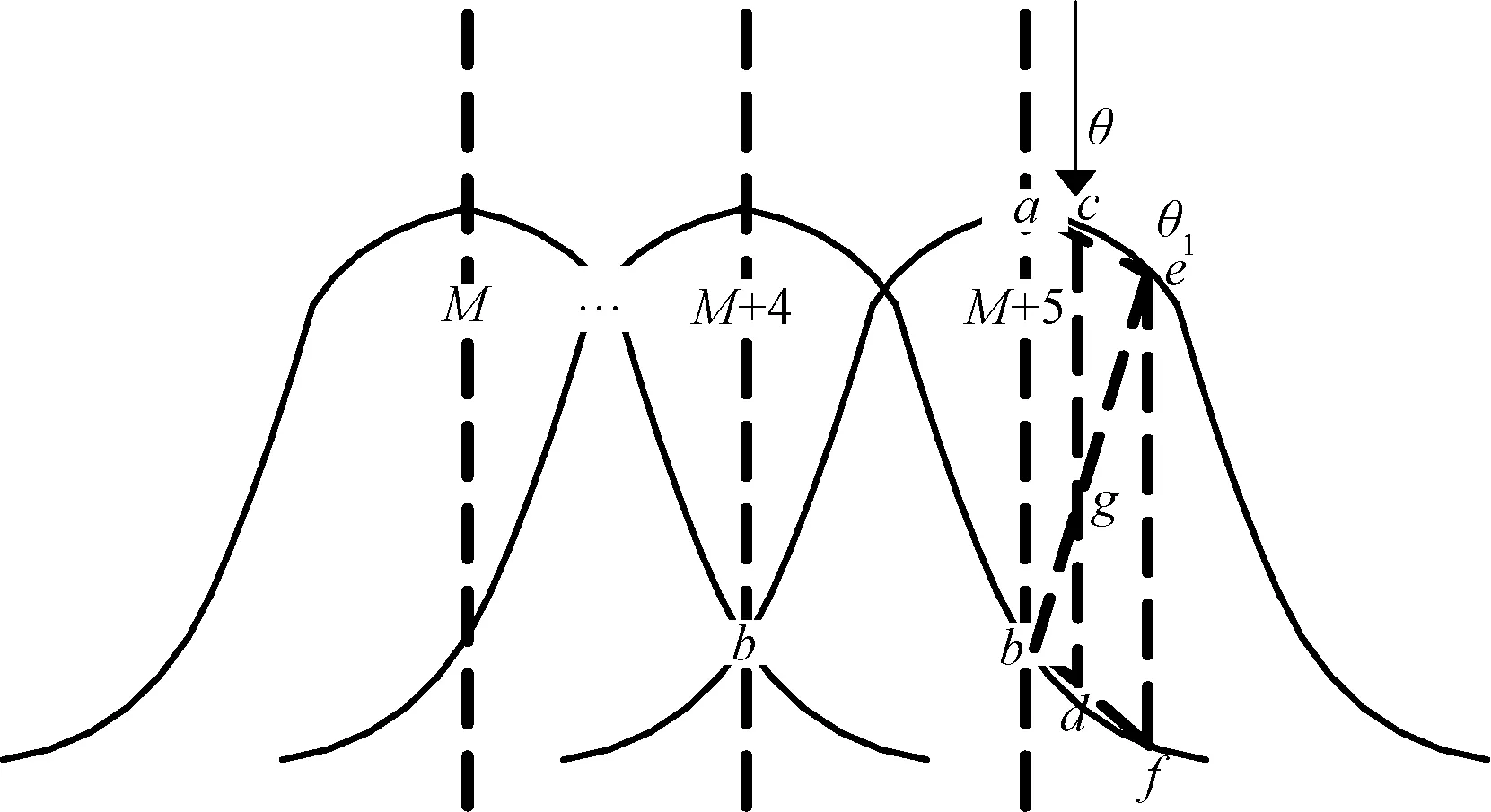
图7 边波束梯形近似原理
设θ方向入射的信号分别与M+5、M+4号波束交叉于Ac、Ad点。在θ外侧取θ1交M+5、M+4号波束于Ae、Af点。M+5号波束顶点Aa作垂线交M+4号波束于Ab点。e、g点与c、d连线交点为g。由三角近似的原理可得:
(13)
(14)
由上述两式可求出θ为:
(15)
4 测向结果分析

表1 3种算法测向结果
由表1可见,高斯近似由于依赖于方向图的高斯分布,对于如罗特曼透镜这种波束一致性较差方向图测得精度较差;三波束算法与三角近似在边波束以内精度相当,却无法计算边波束的角度值;三角近似结合梯形近似的方法精度较好,计算范围宽,更适用于基于罗特曼透镜的比幅测向系统。
5 结束语
本文介绍了基于罗特曼透镜比幅测向系统的工作原理,并以一个六波束比幅测向系统为例,分析了几种不同算法分析此问题的优劣,说明了算法应用中的优化技巧。发现以三角近似的方法与梯形近似优化结合,能够得到较好的测向精度。今后,将以进一步提高测向精度为目的,以更多波束、更宽频带的透镜为例,进一步研究算法可行性。
[1] 吴鹏.一种数字信道化接收机参数编码方法[J].电子世界,2014(1):107-108.
[2] 赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社,2003.
[3] 桂盛,姚申茂.罗特曼透镜馈电的多波束阵列系统设计[J].舰船电子对抗,2014,37(4):102-107.
