外场条件下信噪比估计算法应用研究

高墨昀，顾 军，柴 恒

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

雷达信号的信号功率与噪声功率之比，称为信噪比(SNR)，是雷达信号侦收的一个重要指标，单位为分贝(dB)。接收信号的信噪比估计，对于雷达信号的截获和识别来说是非常重要的。高信噪比的截获信号，是雷达信号特征能够准确提取的前提，也是进行信号源识别工作的基础。接收信号信噪比估计的准确性直接影响雷达信号处理准确率和相关算法计算结果的正确性。

对于给定调制方式信号的信噪比估计，可以分为恒包络和非恒包络两大类。恒包络信号的信噪比估计算法较简单，根据平方信噪方差比(SNV)估计法[1]，可以将信号包络的变化归结为噪声的影响，把信号包络的方差作为噪声的功率，信号包络均值的平方作为信号功率，可以较为准确地估计出信号的信噪比。计算公式如下：

(1)

式中：a(n)为信号瞬时包络。

对非恒包络信号的信噪比估计已经有了一些方法。早在1996年，Andersin等利用训练序列来构造接收信号的相关矩阵，通过噪声子空间投影或信号子空间投影分离信号与干扰和噪声得到信噪比的估计[2]。Pauluzzi在文献中论述了几种常用的基于高斯信道的信噪比估计算法，并做了很好的总结比较[3]。下文将对非恒包络信号的信噪比估计算法进行具体分析。

1 几种常见信噪比估计算法分析

对非恒包络信号的信噪比估计，目前理论分析比较成熟的经典信噪比估计算法有：

(1) 最大似然估计(ML)法：利用训练序列或判决反馈序列来构造似然函数，属于一种自适应算法。这种算法获得的信噪比估计是有偏差的，Thomas引入了修正因子可以减少这一偏差[4]；

(2) 二阶四阶矩(M2M4)估计法：利用信号和噪声的2、4阶矩之间的关系来估计信噪比；

(3) 信号投影(SP)估计法：通过信号投影算法分别得出干扰功率的投影表达式和信号功率的投影表达式，从而得到信噪比估计；

(4) 信号子空间分解(SB)估计法：针对窄带信号，利用训练序列来构造接收信号的相关矩阵，基于信号子空间分解来得出信号与噪声功率的估计，从而计算出较为精确的实时信噪比。

此外，针对上述几种算法存在的不足，又有一些新的算法出现，如高阶累积量估计法、自相关矩阵奇异值分解(SVD)估计法、数据拟合估计法等等。下面针对M2M4估计法和自相关矩阵奇异值分解估计法进行详细的介绍。

1.1 自相关矩阵奇异值分解(SVD)估计法

调制信号s(n)通过一加性高斯白噪声(AWGN)信道，接收信号无失真采样后由下式表示：

y(n)=s(n)+w(n)

(2)

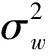
则接收信号的自相关矩阵Ry为：

Ry=E{y(n)yH(n)}=

E{[s(n)+w(n)][s(n)+w(n)]H}=

E{[s(n)+w(n)]}+E{[s(n)+w(n)]H}=

Rs+Rw

(3)

式中：H表示共轭转置；自相关矩阵阶数为m。

根据信号空间分解法，R矩阵可被分解成信号子空间和噪声子空间。由于上式中3个矩阵Ry、Rs、Rw均为对称阵，则经特征值分解后，可表示为：

Rs=UΛsUH

(4)

Rw=UΛwUH

(5)

式中：U为一正交矩阵；Λs为一个秩p小于其阶数m的对角矩阵：

Λs=diag(γ1,γ2,…,γp,0,…,0)m×m

(6)

式中：γ1≥γ2≥…≥γp。

(7)

代入公式Ry=Rs+Rw后可得：

Ry=Rs+Rw=U(Λs+Λw)UH=U(Λy)UH

(8)

其中：

Λy=diag(λ1,λ2,…,λm)m×m=

(9)

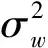
(10)

1.2 二阶四阶矩(M2M4)估计法

二阶四阶矩估计法是一种自适应算法，由于其是基于接收信号的二阶和四阶量估计，从而不需要相位恢复。作为累计量算法，它不需要接收机判决，因此是一种无辅助数据估计算法。

早在1967年，Benedict和Soong就提出了二阶和四阶矩应用于实加性高斯白噪声(AWGN)信道中载波和噪声的估计[6]。Matzner等也在这方面做了不断的研究。在他们的研究基础上可以得出对于实信道和复信道中信噪比的估计方法。

假设接收信号y(n)与噪声都是零均值、相互独立的随机过程，并且复噪声的同相和正交2路相互独立，则信号的二阶量M2和四阶量M4可以简化表示为：

M2=S+N

(11)

M4=KaS2+4SN+KwN2

(12)

其中：

ka=E[an4]/(E[an2])2

(13)

kw=E[wn4]/(E[wn2])2

(14)

联立两式可以推出信号、噪声的估计值：

(15)

N=M2-S

(16)

此处S与N的比值即为信噪比。

对于多进制相移键控(MPSK)信号来说，ka=1；对于复噪声来说，kw=2，因此可得：

(17)

(18)

在实际应用中，二阶和四阶量是由接收信号的时间平均来计算的，下面给出它们的近似表达式，对于实信道或复信道都适用：

(19)

(20)

式中：N为接收信号时域宽度。

2 算法仿真

以常见的AWGN信道为例，假设信道为理想信道，以恒包络信号常用的平方信噪方差比估计法作为对照，对上述M2M4估计算法和自相关矩阵奇异值分解估计法等2种估计算法的性能分别进行测试，对其均方误差加以比较。选取仿真软件为Matlab R2013a。

仿真试验中，接收信号由软件生成。为了提高所模拟信号的逼真度，以软件生成的相位调制信号作为输入信号，以均值为0、正态分布的随机数发生器产生高斯噪声序列，作为加性高斯白噪声的仿真。

主要对3种估计算法在不同信噪比下的信噪比估计值结果进行了仿真研究。生成信号为二进制相移键控(BPSK)信号，其载频为120 MHz，采样频率600 MHz。取信号长度为4 000，对-6～30 dB范围信噪比作仿真计算各500次，得到信噪比估值的均值、方差和标准差，如图1～图3所示。

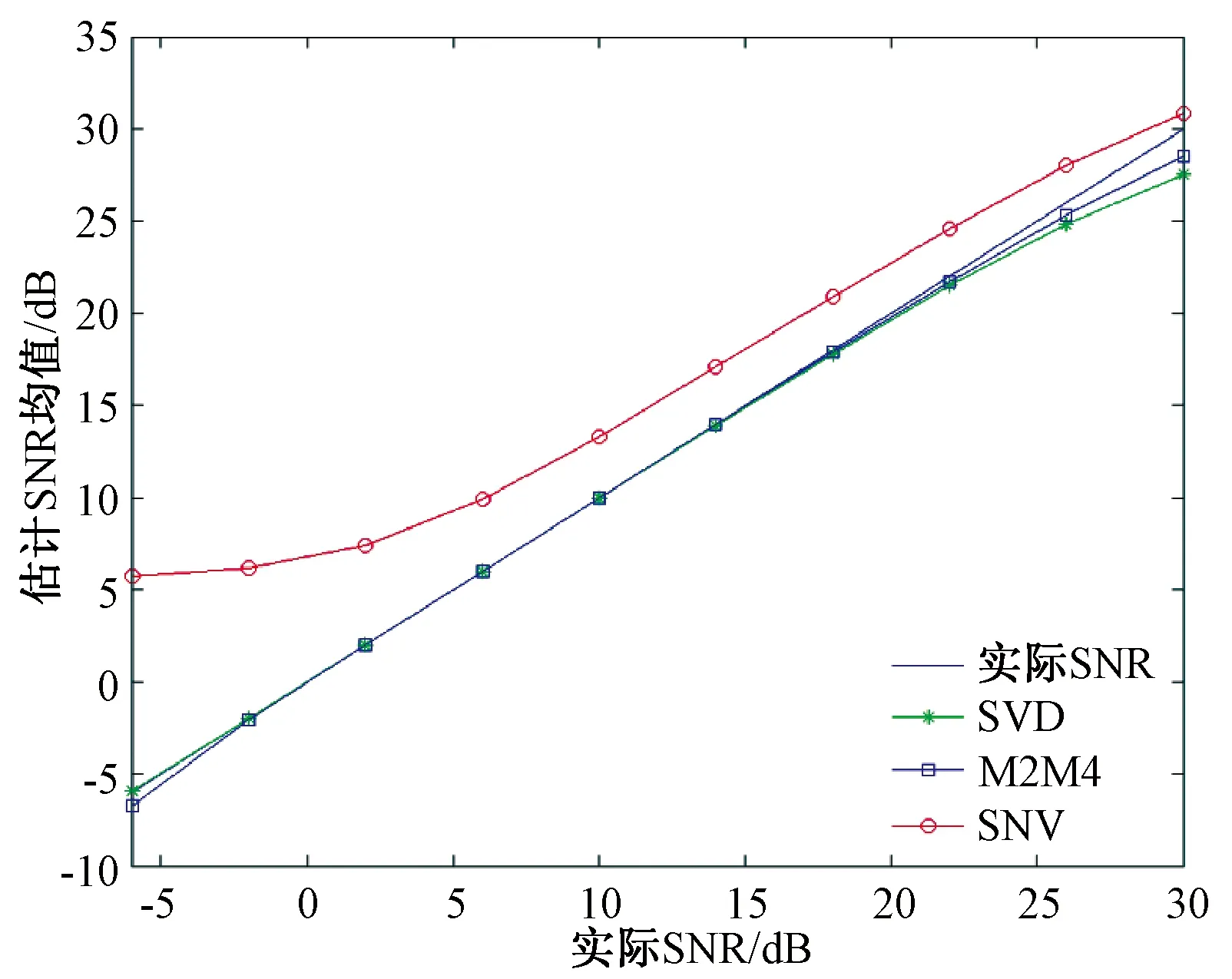
图1 3种方法在不同SNR实际值下SNR估计的均值

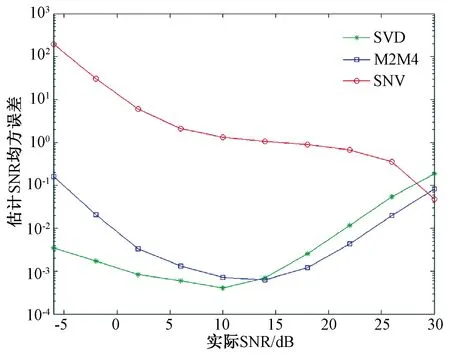
图2 3种方法在不同SNR实际值下SNR估计的均方误差

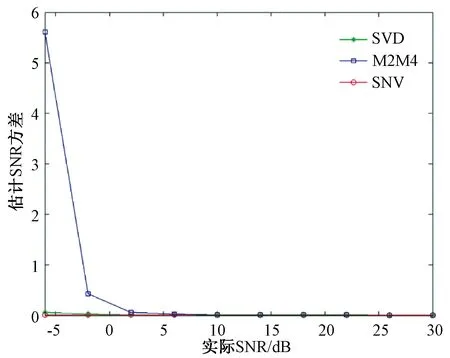
图3 3种方法在不同SNR实际值下SNR估计的方差

由图可得，平方信噪方差比估计法的SNR估计值较实际值总体偏大，误差较高，且在低信噪比条件下偏离得更多；M2M4法在高信噪比和低信噪比条件下均略微偏小，而在0～20 dB范围内的估值较为准确；自相关矩阵奇异值分解法在中低信噪比条件下的估值较为准确，而仅在信噪比高于25 dB条件下的准确性略逊于M2M4法。

在3种方法的稳定性方面，M2M4法和自相关矩阵奇异值分解法估计值的均方误差均低于平方信噪方差比估计法，其中自相关矩阵奇异值分解法的均方误差在低信噪比条件下低于M2M4法，而在高信噪比条件下较之要高。3种方法在信噪比大于5 dB时的SNR估计值方差都比较低，但M2M4法的方差在低信噪比时远高于平方信噪方差比估计法和自相关矩阵奇异值分解法。

综合分析可知，M2M4法和自相关矩阵奇异值分解法的SNR估计较为准确，但M2M4估计法的稳定性在低信噪比条件下不及自相关矩阵奇异值分解法。

3 外场实测

在电磁环境复杂的外场条件下，以实际侦收到的某型雷达脉冲信号作为待测信号，选取信噪比较高的同调制方式同脉宽脉冲共100个，对上述仿真试验中的3种信噪比估计算法的实际性能和效果做一评估。

实际测得，通过平方信噪方差比估计法、M2M4法和自相关矩阵奇异值分解法计算100个脉冲的信噪比估计值平均值分别为32.86 dB，31.39 dB和29.86 dB，如图4、图5所示。由图4可以看出，通过自相关矩阵奇异值分解法与M2M4估计法得出的SNR估计值均低于平方信噪方差比估计法，符合仿真结果的预期，但是自相关矩阵奇异值分解法的实测SNR估计值略大于M2M4估计法。同时由图6可知自相关矩阵奇异值分解法的SNR估计方差在3种算法当中是最小的，这表明在信噪比为30 dB左右时，自相关矩阵奇异值分解估计算法的稳定性最好。

图4 外场条件下3种方法的SNR估计

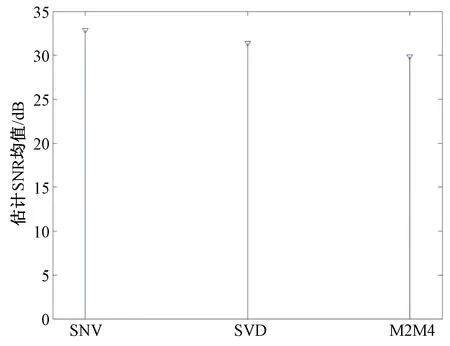
图5 外场条件下3种方法的SNR估计均值

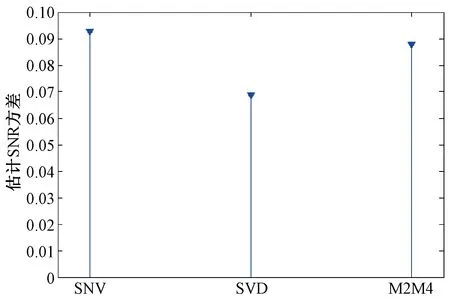
图6 外场条件下3种方法的SNR估计方差

4 结束语

本文详细分析了自相关矩阵奇异值分解法和M2M4估计法2种信噪比估计算法，并对该2种算法进行了加性高斯白噪声的Matlab仿真计算，以及将算法应用到外场条件下实际截获到的脉冲。算法仿真结果表明：在低信噪比条件下，M2M4估计法的准确性和稳定性不及自相关矩阵奇异值分解法；而在信噪比较高时，M2M4法的准确性略优于自相关矩阵奇异值分解法，但两者差异较小。在外场条件下的实际应用结果表明：自相关矩阵奇异值分解法的SNR估计值与M2M4估计法接近，但方差更小，算法更加稳定，基本与仿真结果相吻合。

[1] GILCHRIEST C E.Signal-to-noise monitoring[J].JPL Space Programs Summary,1966,4(37-27):169-184.

[2] ANDERSIN M,MANDAYAM N B,YATES R D.Subspace based estimation of the signal to interface ratio for TDMA cellular systems[C]//IEEE Vehicular Technology Conference.Atlanta,GA:IEEE,1996:1155-1159.

[3] PAULUZZI D R,BEAULIE N C.A comparison of SNR estimation techniques for the AWGN channel[J].IEEE Transactions on Communications，2000，48(10):1681-1691.

[4] THOMAS C M.Maximum liklyhood estimation of signal-to-noise ratio[D].Los Angeles:University of Southern California,1967.

[5] 张贤达.现代信号处理[M].北京:清华大学出版社,1995.

[6] BENEDICT T R,SOONG T T.The joint estimation of signal and noise from the sum envelope[J].IEEE Transactions on Information Theory,1967:13(3)：447-454.