上行小小区网络采用累计分布函数的资源分配

王建伟， 张海林

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

小小区通信可以提升网络容量，优化网络覆盖，为用户提供更好的使用体验，成为5G移动通信的关键技术之一[1]．然而，小小区通信采用共信道模式，会产生严重的同频干扰，尤其在上行链路中，各小区基站无法预知其他小区用户的干扰，系统性能和用户服务质量(Quality of Service，QoS)会受到严重影响[2]．

小小区蜂窝异构网络中的公平性资源分配一直是研究热点．文献[3]在宏小区用户干扰约束下，研究了家庭基站网络中的资源分配问题，以保证资源分配的公平性．文献[4]提出了一种联合信道分配和功率分配算法，实现了系统容量最大化， 但是文中没有考虑小小区对宏基站的干扰．博弈论作为一种有效工具，已经广泛用于通信资源分配问题中[5-6]．随着基站端天线数目和用户数目的不断增大，集中式资源分配会产生大量的系统开销，分布式算法可以有效降低系统复杂度．文献[7]提出了一种基于累计分布函数的调度(Cumulative distribution function-based Scheduling，CS)算法．在CS算法中，系统认为每一个用户的速率为独立同分布随机过程，用户的平均速率和其他用户的速率分布无关．这一特性使CS算法广泛应用于下一代无线通信中的多个场景[8]．然而，CS算法在上行异构网络中应用较少．

针对上述文献的不足，笔者考虑上行小小区网络场景，采用一种基于累计分布函数的资源分配策略．首先基站使用CS算法为小小区用户进行信道分配，然后提出了一种简化的、分布式功率分配算法．

1 系统模型

文中考虑上行蜂窝异构网络，包括1个宏基站和S个小小区，每个小小区包含K个用户．假定在给定的时隙内，一个小小区只能为一个用户服务．

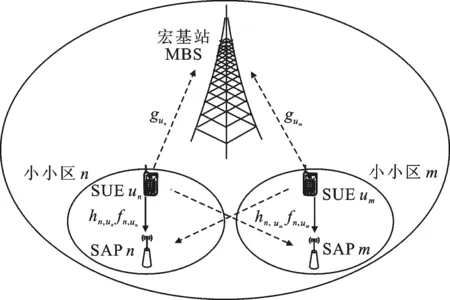
图1 系统模型

系统模型如图1所示．令hm，unfm，un代表小小区n(n∈ {1，2，…，S})中的用户un(un∈ {1，2，…，K})到服务接入点(Service Access Point，SAP)m(m∈ {1，2，…，S})之间的信道增益，其中hm，un代表大尺度衰落，在给定的时隙内值为常数且不变;fm，un代表小尺度快衰落; 设定用户和接入点之间的快衰落信道为瑞利衰落信道，fm，un独立同分布，且均值为0;gun代表小小区n中的用户un到宏基站(Macrocell Base Station，MBS)的信道增益;pun代表用户SUEun的发射功率;aun代表SUEun的信道分配指数．如果小小区SAPn为用户SUEun服务，则aun=1；如果SAPn不为SUEun服务，则aun=0．

综上，小小区用户SUEun在本小区接入点SAPn端的瞬时信干噪比可以表示为

(1)

其中，P=[p1，p2，…，pS]，为各用户发射功率矩阵，σ2代表系统背景噪声．根据香农公式，在单位带宽内，用户SUEn的传输速率Rn，un(P)= lb(1+ηn，un(P))．

以系统的容量最大化为目标，在满足小小区用户在宏基站端的总功率一定，以及保证用户正常通信的前提下，此问题可用如下最优化问题P1表示:

(2)

2 基于累计分布函数的用户调度

假设在给定的时隙和频带内，用户u1，u2，…，uS被选定传输数据，发射功率为p，则式(1)可以转化为

(3)

其中，γn，um代表其他用户静默，用户um在小小区基站SAPn端的信噪比．γn，um符合指数分布，其累积分布函数(Cumulative Distribution Function，CDF)可以表示为

(4)

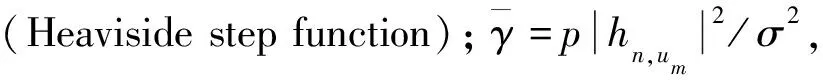
在信道估计阶段，小小区基站向用户发送导频信号，用户根据接收到的信号可以获得用户和基站之间的信道状态信息，即信噪比，通过一段时间的观察，进而获取信噪比的累计分布函数Cn，um(γ)．在给定的时隙，用户计算瞬时信噪比，将该时隙的信噪比CDF值反馈给基站，基站从本小区所有用户的反馈值中选取CDF值最高的用户，从而进行下一阶段数据传输．

3 最优的功率分配

进行数据传输的用户，通过功率控制，大大降低了对其他同频用户的干扰，可认为系统运行在高信干噪比区域，即η远大于1．因此，用户数据速率可进行如下近似:Rn，un(P)= lb(ηn，un(P))．

系统容量可以写成

(5)

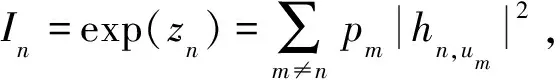
(6)

根据文献[9]，上述问题是一个凸优化问题，式(6)的拉格朗日形式可以转化成S个子问题，即

(7)

拉格朗日乘数因子λ、μ和ν分别对应基站端总功率约束; 单个用户QoS约束和同频用户干扰约束．上述子问题的拉格朗日形式可表示为

可以采用次梯度迭代算法，通过t+1次迭代得到各拉格朗日因子，即

其中，δ为迭代步长，[X]+=max{X，0}．根据KKT(Karush-Kuhn-Tucker)条件，最优的传输功率可以通过对拉格朗日公式求导获得，即∂Ln(yn，Zn，λ，μn，νn) ∂yn=0，结果如下:

(12)

由以上算法可以看出，虽然采用标准的最优化算法进行求解，但是在收敛之前，基站和用户端需要进行大量的信号交互．当基站和用户数目变大时，系统开销过大，全局最优功率分配算法不再实用．

4 基于CDF的分布式功率分配

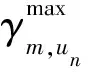
当所有小小区采用基于CDF调度算法，用户SUEn在SAPn的信干噪比下限可以表示为η≥ηn，un(1+ (S- 1)γth)．文献[10]给出的用户速率下界表达式为

(13)

由式(13)可以看出，用户速率下界是关于用户到各小小区接入点信道状态信息和信噪比门限γth的函数，与小区间同频干扰无关．通过设置合适的信噪比门限，全局优化问题可以转化为分布式最优问题．问题P2中的用户QoS约束则可以转化为线性约束条件．分布式优化问题P3可以表示为

(14)

采用和问题P2相同的方法进行求解，获取用户的最优发送功率．同全局最优功率分配算法相比，分布式功率分配只要设置合适的信噪比门限值γth，用户不需要广播各自的信道状态信息，可以减少系统开销，降低运算复杂度．

5 计算机仿真

图2给出了小小区用户数目不同时，系统容量随信噪比门限变化的曲线．由图2可以看出，基于CDF的用户调度策略，可以利用多用户分集，当用户数目变大时，系统容量可以得到有效提升．其次，信噪比门限可以作为一个独立的参数，通过设置合适的信噪比门限，可以获取最佳的系统性能．当信噪比门限变大时，用户发送功率变大，对其他小区产生的干扰变大，从而降低系统容量．当信噪比门限大于一定数值时，系统容量为零，两条曲线有相交的趋势．

图3给出了系统容量随功率衰减因子变化的曲线．当小小区用户的功率衰减因子很小时，用户SUEn对其他小小区造成的同频干扰比较小，增大功率衰减因子，提高用户发射功率，则系统容量变大．当功率衰减因子超过某一门限值时，用户SUEn会对其他小小区用户造成严重的同频干扰；当继续增大发射功率时，则会降低系统容量．仿真结果表明，基于CDF分布式功率分配算法同全局最优功率算法相比，性能损失不大．

图4给出了全局最优功率分配算法同分布式功率分配算法收敛速度对比，初始化用户功率衰减因子为1，向下搜索最优解．可以看出分布式功率分配具有更快的收敛速度，系统开销较小．

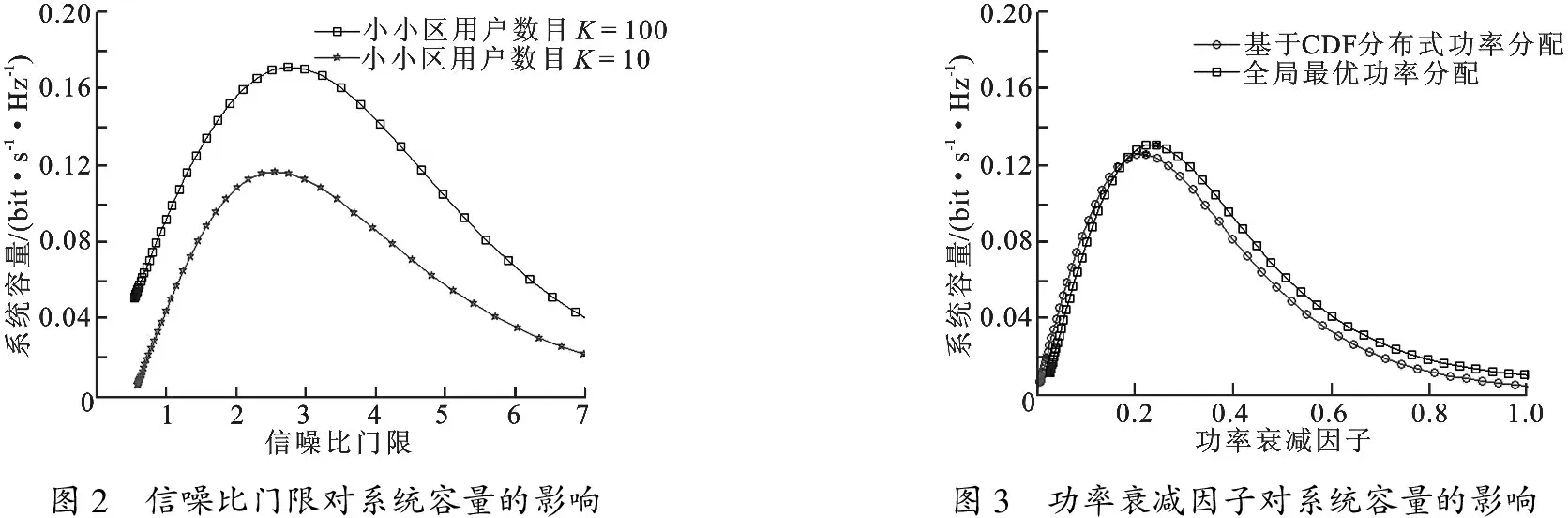
图2 信噪比门限对系统容量的影响图3 功率衰减因子对系统容量的影响

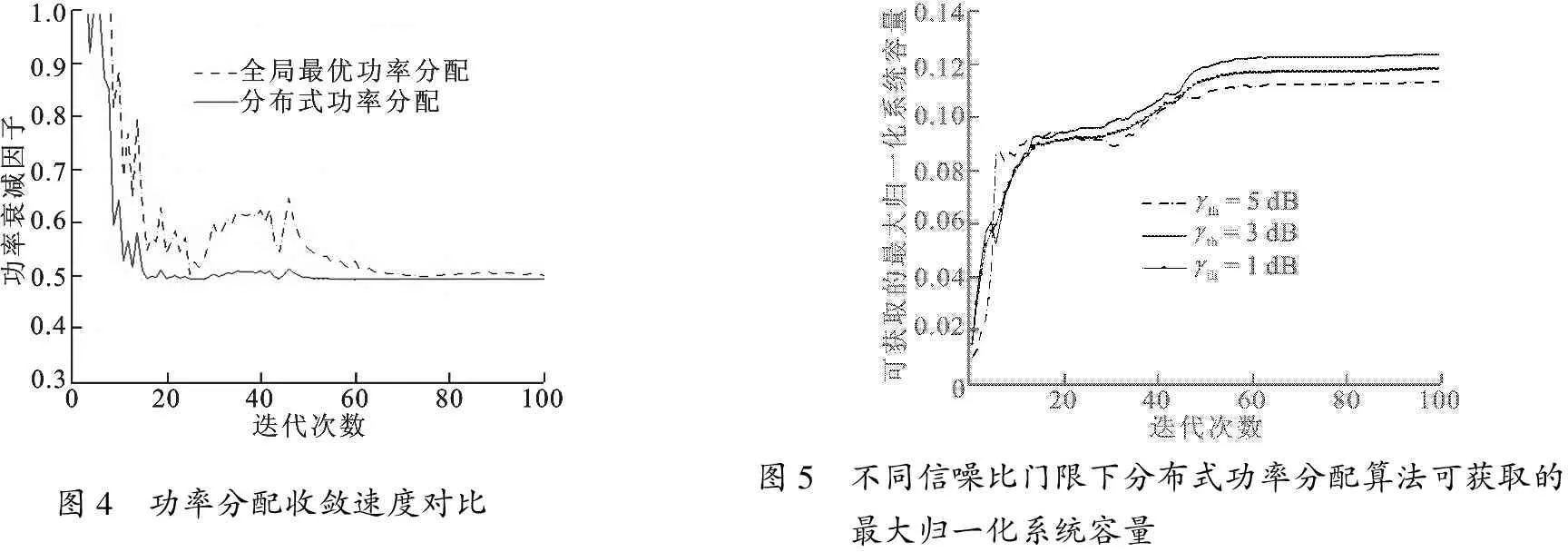
图4 功率分配收敛速度对比图5 不同信噪比门限下分布式功率分配算法可获取的最大归一化系统容量

图5给出了不同信噪比门限下分布式功率分配可获取的最佳系统性能，与图4中全局最优功率分配算法相比，其收敛更快．与图2相比，分别设置不同的信噪比门限，分布式功率分配可以获取不同的系统性能．当信噪比门限较小时，对应信噪比门限γth= 1 dB，用户发送功率较小，系统和速率较小；当信噪比门限取合适值时，对应γth= 3 dB，分布式功率分配算法可以获取最优的系统性能；当信噪比门限较大，对应γth= 5 dB 时，用户发送功率变大，对其他小区产生较大的同频干扰，系统和速率变小．

6 结 束 语

为了解决上行蜂窝异构网络中资源分配问题，文中提出一种基于CDF的用户调度策略和分布式功率分配算法．基于CDF的用户调度，利用多用户分集，当用户数目变大时，可以提升系统的容量．全局最优功率分配可以使系统容量最大化，但是由于开销过大，当基站和用户数目变大时，不再实用．基于CDF的分布式功率分配算法可以有效降低复杂度，并且系统性能损失不大．

[1] JUNGNICKEL V, MANOLAKIS K, ZIRWAS W, et al. The Role of Small Cells, Coordinated Multipoint, and Massive MIMO in 5g[J]. IEEE Communications Magazine, 2014, 52(5): 44-51.

[2] SHENGM, LIU G, WANG X, et al. Interference Alignment and Cancelation for the Uplink of Heterogeneous Networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(2): 1104-1115.

[3] HA V N, LE L B. Fair Resource Allocation for OFDMA Femtocell Networks with Macrocell Protection[J]. IEEE Transactions on Vehicular Technology, 2014, 63(3): 1388-1401.

[4] KIM J, CHO D H. A Joint Power and Subchannel Allocation Scheme Maximizing System Capacity in Indoor Dense Mobile Communication Systems[J]. IEEE Transactions on Vehicular Technology, 2010, 59(9): 4340-4353.

[5] 曹傧, 孙曦, 李云, 等. 考虑竞争的纳什均衡协作通信传输策略[J]. 西安电子科技大学学报, 2015, 42(6): 145-151.

CAO Bin, SUN Xi, LI Yun, et al. Nash Equilibrium Cooperative Transmission Strategy Considering Competition[J]. Journal of Xidian University, 2015, 42(6): 145-151.

[6] 杜白, 李红艳. 一种采用剩余服务时间的异构网络选择算法[J]. 西安电子科技大学学报, 2016, 43(1): 7-11.

DU Bai, LI Hongyan. Network Selection Algorithm in Heterogeneous Wireless Networks Based on Residual Sevice Time[J]. Journal of Xidian University, 2016, 43(1): 7-11.

[7] PARKD, SEO H, KWON H, et al. Wireless Packet Scheduling Based on the Cumulative Distribution Function of User Transmission Rate [J]. IEEE Transactions on Communications, 2005, 53(11): 1919-1929.

[8] ZHENG. Z, HAMALAINEN J, DING Z. On the Sum Rate of Fair Resource Allocation with Selective Feedback[J]. IEEE Transactions on Wireless Communications, 2016, 15(8): 5193-5205

[9] BOYD S, VANDENBERGHE L. Convex Optimization [M]. Cambridge: Cambridge University Press, 2004.

[10] JIN H, JUNG B C, LEUNG V C M. On the CDF-based Scheduling for Multi-cell Uplink Networks[C]//Proceedings of the 2014 IEEE International Conference on Communications. Piscataway: IEEE, 2014: 5012-5017.