无人机中继广播通信系统航迹优化方法

李冬霞， 李春鸣， 赵文强， 刘海涛

(中国民航大学 天津市智能信号处理与图像处理重点实验室，天津 300300)

中继通信是无人机(Unmanned Aerial Vehicle，UAV)应用的一个重要领域．与传统的固定中继通信相比，无人机中继通信具有部署方便、网络构建迅捷、通信覆盖范围大等诸多优点，因此，近年来无人机中继通信在军用与民用领域获得广泛关注[1-2]．特别是无人机中继广播通信技术，在军事通信中的应用越来越显示出其独特的优势，成为未来局部战争的重要技术手段．与此同时，无人机中继通信也面临一系列新的技术挑战，例如无人机中继航迹优化问题，系统链路传输可靠性问题等．

目前，无人机中继通信的研究主要集中在以下4个方面: 无人机中继网络性能优化[3-4]，无人机空地通信信道建模[5]，无人机中继通信传输方法[6]，无人机中继航迹优化[7-10]．其中，无人机中继航迹优化是提高通信系统服务质量的重要技术手段．为解决无人机中继点对点通信系统的航迹优化问题，文献[7]提出基于发射与接收波束成形的无人机中继传输方法，并给出了基于信噪比最大化准则的中继无人机航迹优化方法; 文献[8]提出了基于人工势场法的无人机航迹优化方法，该方法采用多架无人机作为中继平台，极大地提升了链路的传输容量．为解决多用户接入无人机中继系统的航迹优化问题，文献[9]基于和速率最大化准则，分别给出了空分多址和时分多址两种传输方式下的中继无人机航迹优化方法;文献[10]基于最小各态历经链路容量最大化准则给出了无人机航迹优化方法．上述文献仅讨论了点对点和多用户接入无人机中继通信系统的航迹优化问题，没有涉及到无人机中继广播通信系统航迹优化问题．

针对无人机中继广播通信系统性能优化问题，文献[11]基于多架中继无人机总发射功率最小化准则提出了一种无人机位置部署及其覆盖区域划分的联合优化方法．然而，该方法仅考虑了无人机至用户节点单跳链路，没有考虑基站至无人机链路对系统性能的影响．针对同样的问题，文献[12]基于中断概率最小化准则提出了中继无人机的最优位置部署及功率分配方法．然而，文献采用旋翼无人机作为中继平台，所采用的方法能否应用到固定翼无人机中继通信系统还需要进一步的验证．

考虑到固定翼无人机中继广播通信系统在实际应用中发挥着重要作用，笔者针对固定翼无人机中继广播通信航迹优化问题，提出了基于用户节点平均中断概率最小化准则的无人机航向角的优化方法，给出了单用户节点中断概率计算公式，并仿真验证了笔者提出方法的正确性；最后分析了无人机最大转弯角和服务区域半径对最优航迹和系统性能的影响．

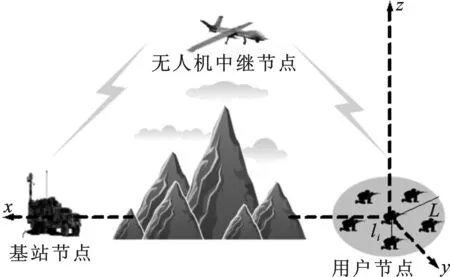
图1 无人机中继广播通信系统模型

1 系统模型

1.1 系统模型

图1给出了无人机中继广播通信系统的模型．系统由固定基站(Base Station，BS)节点、机动飞行的无人机中继节点及N个用户(ui，i=1，…，N)节点组成．其中，基站节点位于地面，无人机搭载中继载荷以固定高度h、恒定速度v飞行，N个用户节点均匀分布在地面一个圆形服务区域内．

假设基站节点与服务区域距离较远，不存在基站节点到各个用户节点的直达通信链路，则必须通过无人机的中继才能够实现基站节点与各个用户节点的广播通信．此外，假设基站节点、无人机中继节点及各用户节点均配置单个天线．

为方便计算基站与无人机节点及无人机节点与各个用户节点的距离，按照以下方式建立三维直角坐标系: 以圆形服务区域的中心作为笛卡尔直角坐标系的原点，以坐标原点与基站连线的方向作为直角坐标系的x轴，以坐标原点垂直于大地向上的方向作为直角坐标系的z轴．假设基站节点与直角坐标系原点的距离为R0，则基站节点的坐标为[R0，0，0]．此外，为方便描述各个用户节点在服务区内的分布情况，以直角坐标系的原点作为极坐标系原点，以直角坐标系的x轴方向为极坐标系零度极角方向建立极坐标系，则所有用户节点均匀分布于极坐标系下以原点为中心、半径为L的圆形区域内．

1.2 信号模型

在无人机中继广播通信系统中，无人机采用放大转发模式工作．第1个时隙，基站节点发射信号s，无人机中继节点接收信号表示为

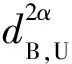
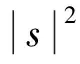
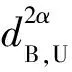
i=1，2，…，N，(2)

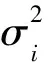
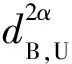
2 无人机航迹优化方法

2.1 单用户节点近似中断概率

中断概率定义为接收信噪比低于某一门限值γth的概率，是衡量无线通信系统连通性能的一项重要指标．为了便于优化处理，降低计算复杂度，以用户节点的近似中断概率作为性能优化指标．以下分析给出其具体的数学描述．

利用式(3)，可计算得到用户ui节点的中断概率近似表达式[13]:

(4)

(5)

考虑到无人机飞行高度恒为h，在t时刻，基站节点、无人机中继节点及用户节点ui的三维笛卡尔坐标分别为b= [R0，0，0]T，rt= [xt，yt，h]T和ui= [xi，yi，0]T，由此可计算得到dB，U与dU，i，并将其代入式(5)，得到t时刻用户ui节点的近似中断概率:

(6)

式(6)表明，在基站与无人机中继节点发射功率及信道输入噪声功率给定的情况下，用户节点ui的中断概率由无人机的位置矢量rt及用户节点位置矢量ui联合决定．在固定翼无人机中继通信系统中，无人机中继节点的位置时刻改变，用户节点的中断概率也随之改变，因此需要依据用户节点的位置及时调整无人机的航迹才能提高系统的连通性能．

2.2 基于平均中断概率最小化准则的航迹优化方法

考虑到系统由多个用户组成，为了提高用户节点的平均连通性能，以服务区内所有用户节点平均中断概率最小化为准则进行航迹优化设计．

假设在极坐标系中用户ui节点的极径为li，极角为θi，则用户ui节点的位置矢量为ui= [licosθi，lisinθi，0]T．考虑到用户节点均匀分布于半径为L的圆形区域内，极径li与极角θi的联合概率密度函数为p(li，θi)= 1 (πL2)，则t时刻圆形服务区内所有用户节点的平均中断概率为

(7)

式(7)表明，给定服务区域半径，所有用户节点的平均中断概率仅取决于t时刻无人机中继节点的位置矢量rt．

进一步根据固定翼无人机的运动模型[7]，假设在t-Δτ时刻无人机中继节点的位置矢量为rt-Δτ= [xt-Δτ，yt-Δτ，h]T，则t时刻无人机在二维平面内的坐标可表示为

(8)

其中，Δτ代表无人机中继节点位置更新的周期，δt代表t时刻无人机中继节点的航向角，满足δt-δt-Δτ≤δmax，其中δmax代表最大转弯角．将式(6)代入式(7)，服务区域内所有用户节点的平均中断概率表示为

Pave(δt)≈γth(ξt+ηtcosδt+ζtsinδt)=γth[ξt+ψtcos(δt-φt)] ,(9)

其中，

式(9)表明，给定t-Δτ时刻无人机中继节点的位置矢量rt-Δτ，t时刻服务区域内所有用户节点的平均中断概率仅取决于t时刻无人机中继节点的航向角δt．至此，基于所有用户节点平均中断概率最小化准则的航迹优化问题表述为

(10)

利用式(9)的结果，以上问题进一步表示为

(11)

通过式(11)对航向角δt求导并使之等于零，同时结合无人机中继节点航向角的约束条件，可计算得到最优航向角为

(12)

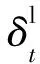
3 性能分析

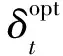
(13)

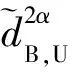
根据中断概率的定义，用户ui节点的中断概率的数学表示为

(14)

(15)

其中，Pr(·)代表概率，fγ1(·)代表γ1的概率密度函数．式(15)可进一步化简[7]为

(16)

其中，Fγ2(·)代表γ2的累积分布函数．

由于基站节点至无人机中继节点及无人机中继节点至用户节点信道的小尺度衰落系数服从瑞利分布，因此γ1和γ2均服从自由度为2的中心卡方分布．γ2的累积分布函数Fγ2(x)与γ1的概率密度fγ1(x)分别为

(17)

将式(17)代入到式(16)中，可得

(18)

其中，K1(·)表示第二类1阶修正贝塞尔函数．令式(18)中μ=γth，即可得到用户ui节点的精确中断概率．

4 数值仿真

4.1 仿真条件

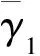
4.2 仿真结果

图2给出了各节点的位置坐标及无人机最优航迹．其中圆形区域代表用户服务区域，“□”代表基站节点位置，“❋”与“○”分别表示无人机中继节点的初始位置及最优中继位置．图2(a)给出了理论和仿真最优航迹的比较图，其中实线为理论分析得到的无人机最优航迹，虚线及点划线分别代表用户数为10及200个用户时，利用穷举法仿真得到的无人机最优航迹．图2(a)结果表明:理论航迹与仿真获得的无人机航迹走势保持一致，且随着用户数的增加，仿真航迹更接近于理论航迹，验证了笔者所提方法的正确性;无人机从初始位置飞行到最优中继位置 [R0/2，0，h]后(参见文献[12])，开始以圆形轨迹飞行，圆的半径为 100 m，周期约为 25 s．图2(b)给出了服务区域半径对最优航迹的影响，其中实线和虚线分别表示服务区域半径为 150 m 与 300 m 时的最优航迹．图示结果表明: 无人机最优航迹不受服务区域半径影响 (α=1)．图2(c)给出了最大转弯角对无人机最优航迹的影响，其中实线和虚线分别表示最大转弯角为15°和25°时的最优航迹．图形观测表明:无人机进入圆形飞行轨迹后，圆的半径随最大转弯角的增加而减小; 当最大转弯角为25°时，无人机圆形飞行路径的半径约为 57.3 m，周期为 14.5 s．

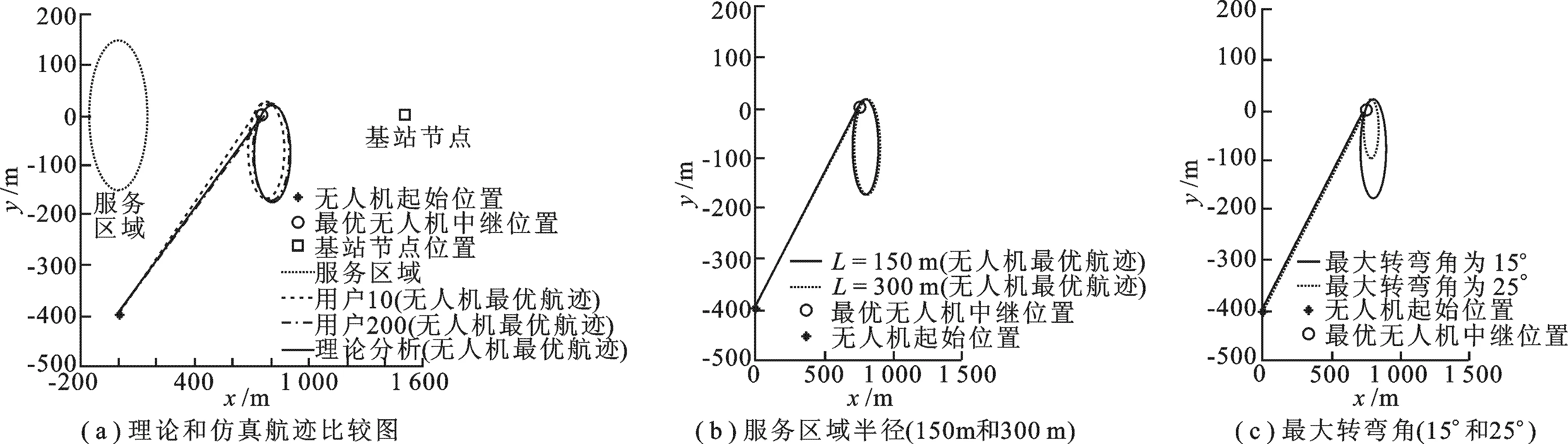
图2 各节点位置及无人机最优飞行航迹

图3给出了服务区域半径和最大转弯角对用户平均中断概率的影响．图3(a)给出了不同服务区域半径下用户节点平均中断概率随时间的变化曲线，其中包含基于用户平均中断概率(见式(9))得到的理论分析曲线和基于精确用户中断概率(见式(18))得到的仿真曲线．图示结果表明:基于用户平均中断概率的近似理论分析曲线与精确仿真曲线非常接近，验证了所提优化方法的有效性．增大服务区域半径，用户平均中断概率增大，系统平均连通性能降低．图3(b)给出了不同最大转弯角下的用户节点平均中断概率曲线．实线和虚线分别表示最大转弯角为15°和25°时，平均中断概率随时间的变化曲线．曲线表明: 随着最大转弯角的增加，用户的平均中断概率减小，系统的平均连通性能提高．

图3 服务区域半径和最大转弯角对用户平均中断概率的影响(10次独立重复实验)

5 结 论

笔者针对固定翼无人机中继广播通信航迹优化问题，提出了一种中继无人机航迹优化方法．该方法有效地实现了中继无人机对其最优中继位置的追踪．研究结论如下:固定翼无人机以恒定速度飞行，飞到最优中继位置后，为了保持系统连通性能最优，开始绕圆在空中盘旋．笔者所提航迹优化方法得到的无人机最优航迹不受服务区域半径的影响 (α=1)，且服务区域半径增大，用户的平均中断概率亦增大．随着最大转弯角的增大，圆形航迹的半径减小，用户的平均中断概率减小，系统的平均连通性能提高．

[1] ZENG Y, ZHANG R, LIM T J. Wireless Communications with Unmanned Aerial Vehicles: Opportunities and Challenges[J]. IEEE Communications Magazine, 2016, 54(5): 36-42.

[2] GUPTA L, JAIN R, VASZKUN G. Survey of Important Issues in UAV Communication Networks[J]. IEEE Communications Surveys and Tutorials, 2016, 18(2): 1123-1152.

[3] 徐赞新, 袁坚, 王钺, 等. 一种支持移动自组网通信的多无人机中继网络[J]. 清华大学学报:自然科学版, 2011, 51(2): 150-155.

XU Zanxin, YUAN Jian, WANG Yue, et al. UAV Relay Network to Provide Communications in Mobile Ad Hoc Networks[J]. Journal of Tsinghua University: Science and Technology, 2011, 51(2): 150-155.

[4] 符小卫, 程思敏, 高晓光. 无人机协同中继过程中的路径规划与通信优化[J]. 系统工程与电子技术, 2014, 36(5): 890-894.

FU Xiaowei, CHENG Simin, GAO Xiaoguang. Path Planning and Communication Optimizing in Multi-UAVs Cooperative Communication relay[J]. Systems Engineering and Electronics, 2014, 36(5): 890-894.

[5] SUN R, MATOLAK D W. Air-ground Channel Characterization for Unmanned Aircraft Systems Part Ⅱ: Hilly and Mountainous Settings[J]. IEEE Transactions on Vehicular Technology, 2017, 66(3): 1913-1925.

[6] CHENG C M, HSIAO P H, KUNG H T, et al. Maximizing Throughput of UAV-relaying Networks with the Load-carry-and-deliver Paradigm[C]//Proceedings of the 2007 IEEE Wireless Communications and Networking Conference. New York: IEEE, 2007: 4420-4427.

[7] OUYANG J, ZHUANG Y, LIN M, et al. Optimization of Beamforming and Path Planning for UAV-assisted Wireless Relay Networks[J]. Chinese Journal of Aeronautics, 2014, 27(2): 313-320.

[8] ZHU M, CHEN Y Y, CAI Z P, et al. Using Unmanned Aerial Vehicle Chain to Improve Link Capacity of Two Mobile Nodes[C]//Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation . Piscataway: IEEE, 2015: 494-499.

[9] JIANG F, SWINDLEHURST A L. Optimization of UAV Heading for the Ground-to-air Uplink[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(5): 993-1005.

[10] CHOI D H, JUNG B H, SUNG D K. Low-complexity Maneuvering Control of a UAV-based Relay without Location Information of Mobile Ground Nodes[C]//Proceedings of the 2014 International Symposium on Computers and Communications. Piscataway: IEEE, 2014: 6912558.

[11] MOZAFFARI M, SAAD W, BENNIS M, et al. Optimal Transport Theory for Power-efficient Deployment of Unmanned Aerial Vehicles[C]//Proceedings of the 2016 IEEE International Conference on Communications. Piscataway: IEEE, 2016: 7510870.

[12] JIN Y, ZHANG Y D, CHALISE B K. Joint Optimization of Relay Position and Power Allocationin Cooperative Broadcast Wireless Networks[C]//Proceedings of the 2012 International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE , 2012: 2493-2496.

[13] SURAWEERA H A, LOUIE R H Y, LI Y, et al. Two Hop Amplify-and-forward Transmission in Mixed Rayleigh and Rician Fading Channels[J]. IEEE Communications Letters, 2009, 13(4): 227-229.