估计偏差修正扩展卡尔曼滤波新算法

邓 兵， 孙正波， 贺 青

(盲信号处理重点实验室，四川 成都 610041)

长期以来，目标跟踪作为一个经典问题，在雷达、通信、声纳、遥测遥控、无线网络等多个领域受到广泛关注[1-4]．典型的无源定位跟踪系统，通过测量目标与传感器之间在时域、频域、空域或能量域的相对关系[5]，应用卡尔曼滤波(Kalman Filter，KF)算法[1-5]、粒子滤波(Particle Filter，PF)算法[6]等获取目标状态估计．而在实际当中，由于测量系统往往是非线性模型，需要采用非线性滤波方法来提高滤波精度．

扩展卡尔曼滤波器(Extended Kalman Filter，EKF)作为一种应用最为广泛的非线性滤波器[2]，其通过对非线性函数进行一阶泰勒级数展开并舍弃高级误差项，将滤波过程中的非线性目标状态估计问题转化为线性估计问题，再利用最优卡尔曼滤波进行状态估计，是一种次优滤波方法．获得一次状态估计以后，在更新的状态估计值附近对原非线性函数重新进行泰勒展开，再次利用扩展卡尔曼滤波器对重新展开的线性函数进行估计，可能会获得更好的估计值，重复迭代这一过程直至收敛，即为迭代扩展卡尔曼滤波器(Iterated Extended Kalman Filter，IEKF)[3-5]．此外，通过计算非线性测量方程的修正函数还发展出了修正增益扩展卡尔曼滤波器(Modified Gain Extended Kalman Filter，MGEKF)[5]，但是修正函数不是任何场景下均存在，影响了此类算法的推广应用．近年来，将粒子滤波器与标准扩展卡尔曼滤波器相结合，利用扩展卡尔曼滤波器产生重要性密度函数，从而形成了扩展卡尔曼粒子滤波器(Extended Kalman Particle Filter，PF-EKF)[6]．但是以上方法均没有克服掉扩展卡尔曼滤波器固有的缺陷，当系统的非线性比较强时，采用局部线性化处理非线性系统估计问题会带来较大的误差，严重时甚至会导致滤波器的发散．文献[7-8]中提出了一种线性校正时差定位算法，通过线性校正非线性定位方程的初始定位结果来提升定位精度．因此，若能够采用线性校正思想对状态滤波结果进行偏差修正，抑制局部线性化所带来的误差影响，将有利于提升目标跟踪精度．

笔者主要考虑在非线性目标跟踪滤波中，利用文献[7-8]中的线性校正思想，结合扩展卡尔曼滤波器滤波算法的特点，通过对扩展卡尔曼滤波器滤波结果偏差进行估计校正来提升跟踪的有效性．首先给出标准扩展卡尔曼滤波的基本流程，在此基础上提出偏差修正扩展卡尔曼滤波算法；然后在时差频差跟踪场景下给出具体的表达式．

1 标准扩展卡尔曼滤波算法基本流程

目标跟踪主要是在目标运动建模的基础上建立状态方程与测量方程，再利用滤波跟踪算法求得目标的状态信息．卡尔曼滤波是线性高斯条件下的状态最优估计解，然而在实际系统中，动态过程和量测过程通常是非线性的，不能直接使用卡尔曼滤波算法．通过泰勒级数展开的方法可以获得非线性系统的近似，进而采用卡尔曼滤波处理非线性系统的滤波问题，这就是扩展卡尔曼滤波．由于采用局部线性化的方法处理非线性滤波问题，扩展卡尔曼滤波算法只有在模型线性化误差较小时才能够获得优良的滤波结果，否则线性化截断误差将会严重影响目标状态的估计精度，甚至使得跟踪结果不收敛．

考虑如下方程所描述的离散时间非线性系统，假定系统中的过程噪声和量测噪声都是加性噪声:

其中，xk∈Rn，表示k时刻的状态向量;zk∈Rn，表示k时刻的量测向量; 非线性函数f(·)和h(·)分别表示动态模型函数和量测模型函数;wk～N(0，Qk)和vk～N(0，Rk)，分别为系统服从零均值高斯分布的过程噪声和量测噪声，其协方差分别为Qk和Rk，两者互不相关．

扩展卡尔曼滤波算法递推步骤描述如下[4]．

步骤2 计算动态系统状态方程的雅可比矩阵:

(3)

步骤3 计算状态估计和估计误差协方差:

(6)

步骤5 计算量测预测、新息协方差矩阵和卡尔曼增益:

步骤6 计算状态估计和估计误差协方差:

相对于其他非线性滤波方法，扩展卡尔曼滤波的优点是使用较为简便，用简单的算法即可获得较好的滤波效果．而且在工程实践上，线性化近似是解决非线性系统问题的常用手段，易于理解和使用，因此可以广泛应用于大多数实际问题中．然而，其缺点在于扩展卡尔曼滤波在非线性度较高的系统中无法获得满意的滤波效果，线性化截断误差对目标状态估计结果影响明显，严重时甚至导致跟踪发散．

迭代卡尔曼滤波[5]通过将式(10)获得的目标状态估计带回式(6)重新计算Hk，并重复步骤5至步骤6直至收敛．实际当中往往限制迭代次数以增强算法的时效性．

2 线性校正扩展卡尔曼滤波算法

(12)

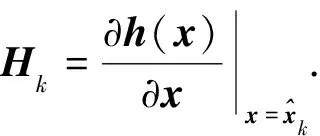
(13)

根据最小二乘原理，可以得到

(14)

其中，W为加权矩阵，W=(R)-1．

则经线性校正后的目标状态最终估计及协方差分别为

至此可以得出偏差修正迭代扩展卡尔曼滤波算法流程图，如图1所示．

图1 偏差修正迭代扩展卡尔曼滤波算法流程图

3 时频差场景下偏差修正迭代扩展卡尔曼滤波算法

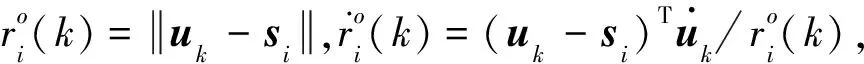
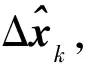
4 仿真结果及分析

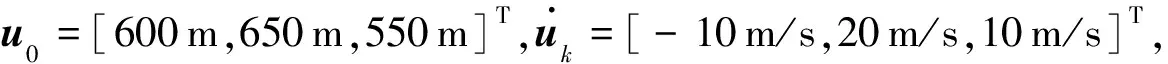
图2和图3分别仿真分析了扩展卡尔曼滤波器、迭代扩展卡尔曼滤波器、修正增益扩展卡尔曼滤波器算法与笔者所提线性校正迭代扩展卡尔曼滤波算法的位置与速度均方根误差．仿真中迭代扩展卡尔曼滤波器及笔者所提算法迭代次数均为3次．从仿真结果可以看出，扩展卡尔曼滤波器由于局部线性化所带来的舍入误差会随着跟踪时间的增加而逐渐增加，严重时会引起滤波发散；迭代扩展卡尔曼滤波器由于增加了迭代过程，能够减小局部线性化误差所带来的影响，但是也不能完全消除；修正增益扩展卡尔曼滤波器由于修正了每次的滤波增益，较扩展卡尔曼滤波器、迭代扩展卡尔曼滤波器算法跟踪性能更优；而笔者所提算法由于在每次滤波后进行了线性校正，较好地克服掉了大部分线性化误差对滤波结果所带来的影响，跟踪收敛性最好．

图2 不同算法位置估计均方根误差图3 不同算法速度估计均方根误差

图4和图5为笔者所提线性校正扩展卡尔曼滤波算法在不同的迭代次数下的跟踪效果．从结果可以看出，随着迭代次数的增加，笔者提出算法的性能也得到增强．

此外，相比于迭代扩展卡尔曼滤波器算法，文中增加了线性校正过程，算法的复杂度有所增加，但增加不多．为验证上述分析，在MATLAB R2009b仿真条件下，经统计，在 60 s 数据长度下，运算200次扩展卡尔曼滤波器、迭代扩展卡尔曼滤波器(迭代次数为3次)、修正增益扩展卡尔曼滤波器以及笔者所提算法(迭代次数为3次)的计算总时间分别为 2.213 4 s、5.962 6 s、3.235 2 s、6.531 8 s，符合预期．

图4 不同迭代次数下位置估计均方根误差图5 不同迭代次数下速度估计均方根误差

5 总 结

针对实际当中非线性目标跟踪滤波问题，根据扩展卡尔曼滤波器算法的自身特点，通过增加对滤波结果的偏差修正，利用加权最小二乘算法估计出目标状态估计偏差，对原观测矩阵进行更新，并再次滤波，最终得到目标状态估计．仿真分析表明，笔者所提算法相比于扩展卡尔曼滤波器、迭代扩展卡尔曼滤波器以及修正增益扩展卡尔曼滤波器算法具有较好的跟踪性能，能够更好地适应非线性滤波问题．笔者所提的偏差修正滤波思想可以进一步推广到其他非线性滤波算法中，下一步将开展相应的研究工作．

[1] 蔚婧, 文珺, 李彩彩, 等. 辅助变量纯方位目标跟踪算法[J]. 西安电子科技大学学报, 2016, 43(1): 167-172.

YU Jing, WEN Jun, LI Caicai, et al. Modified Instrumental Variable Method for Bearings-only Target Tracking[J]. Journal of Xidian University, 2016, 43(1): 167-172.

[2] LIU Y H, LI T, YANG Y Y, et al. Estimation of Tire-road Friction Coefficient Based on Combined APF-IEKF and Iteration Algorithm[J]. Mechanical Systems and Signal Processing, 2017, 88: 25-35.

[3] YANG Y J, FAN X G, ZHOU Z F, et al. Amended Kalman Filter for Maneuvering Target Tracking[J]. Chinese Journal of Electronics, 2016, 25(6): 1166-1171.

[4] CHEN X Y, XU Y, LI Q H, et al. Improving Ultrasonic-based Seamless Navigation for Indoor Mobile Robots Utilizing EKF and LS-SVM [J]. Measurement, 2016, 92: 243-251.

[5] TIAN Y, CHEN Z, YIN F L. Distributed Iterated Extended Kalman Filter for Speaker Tracking in Microphone Array Networks [J]. Applied Acoustics, 2017, 118: 50-57.

[6] YU H B, WANG G H, CAO Q, et al. A Fusion Based Particle Filter TBD Algorithm for Dim Targets[J]. Chinese Journal of Electronics, 2015, 24(3): 590-595.

[7] 朱国辉, 冯大政, 周延, 等. 一种线性校正TOA定位算法 [J]. 西安电子科技大学学报, 2015, 42(3): 22-25.

ZHU Guohui, FENG Dazheng, ZHOU Yan, et al. TOA Localization Algorithm Using the Linear-correction Technique [J]. Journal of Xidian University, 2015, 42(3): 22-25.

[8] 邓兵, 孙正波, 杨乐, 等. 存在站址误差时的线性校正TDOA定位算法[J]. 西安电子科技大学学报, 2017, 44(4): 252-258.

DENG Bing, SUN Zhengbo, YANG Le, et al. TDOA Localization with Linear-correction in the Presence of Sensor Position Errors[J]. Journal of Xidian University, 2017, 44(4): 252-258.

[9] ZHU G H, FENG D Z. Bi-iterative Method for Moving Source Localisation Using TDOA and FDOA Measurements[J]. Electronics Letters, 2015, 51(1): 8-10.

[10] HU D X, HUANG Z, CHEN X, et al. A Moving Source Localization Method Using TDOA, FDOA and Doppler Rate Measurements[J]. IEICE Transactions on Communications, 2016, E99B(3): 758-766.

[11] DENG B, SUN Z B, YANG L, et al. A Linear-correction TDOA and FDOA Method for Moving Source Localization[J]. IEICE Transactions on Fundamentals, 2017, E100A(4): 1066-1069.