陆地移动卫星信道中的LDPC码分析与优化

戴精科， 林开亮

(1. 火箭军工程大学 信息工程系，陕西 西安 710025；2. 西北农林科技大学 理学院，陕西 西安 712100)

近年来，随着移动通信业务需求的不断增长，陆地移动卫星(Land Mobile Satellite，LMS)系统成为研究热点[1-4]．在移动环境中信号易受到信道衰落的影响，而低密度奇偶检验(Low Density Parity Check，LDPC)码作为一种性能逼近香农极限的先进信道编码技术，具有极强的纠错能力，因此将其应用于陆地移动卫星系统可提高抗衰落能力，改善通信质量．

基于密度进化理论[5]，人们已经获得了低密度奇偶检验码在多种衰落信道中的性能，例如瑞利信道[6]，赖斯信道[7]和Nakagami-m信道[8]等．但是陆地移动卫星信道比较复杂，前述的衰落模型不足以描述所有的信道特征，因此人们提出了多种更精确的理论模型，其中经典的有Loo模型[2]，Lutz模型[9]和阴影-赖斯(Shadowed-Rician，SR)模型[10]等．通过调整相应的参数，这些模型与实际测量的信号特征非常吻合．文献[11]将低轨卫星信道建模为Loo模型，得到了规则低密度奇偶检验码的译码门限，但没有研究不规则码，也未证明码字稳定性条件，这主要是因为Loo模型中衰落系数具有复杂的非闭合概率密度函数(Probability Density Function， PDF)，在数学上很难处理(Lutz模型也是如此)．

阴影-赖斯模型是对Loo模型的修改，其衰落系数的概率密度函数存在闭合形式，降低了理论性能分析的难度．文献[12]推导了最大比值合并系统在阴影-赖斯信道中的误码率，文献[13]研究了正交空时编码在该信道中的性能．文献[14]对低密度奇偶检验码在阴影-赖斯信道中的误码率性能进行了仿真，但未得到性能界(即译码门限)，也没有进行码字度分布优化．笔者证明了阴影-赖斯信道的对称性，推导了稳定性条件和信道容量;利用离散密度进化获得了规则低密度奇偶检验码在该信道的译码门限，并结合差分进化得到了优化的不规则码，其译码门限在最坏信道条件下距离香农极限约0.1 dB，且在相同码长条件下的误码性能优于规则码、高斯信道中优化的不规则码[5]以及新一代数字卫星广播(Digital Video Broadcasting-Satellite-second generation，DVB-S2)标准中的不规则码．

1 阴影-赖斯信道

设传输符号x∈{0，1}，经映射w(w=1-2x)后进行二进制相移键控调制，则解调器输出y的条件概率密度函数为[6]p(y|w，a)= 1/ (2πσ2)1/2exp[-(y-wa)2/ (2σ2)]， 其中噪声方差σ2=S/ (2REb/N0)，R为码率，Eb/N0为信噪比，S=E[a2]．衰落因子a满足阴影-赖斯分布[10]，其条件概率密度函数为

p(a|Z=z)=(a/b0) exp-(a2+z2)/(2b0)I0(za/b0) ,

且a>0．式中，2b0为散射信号分量平均功率；Z=z，为直射信号的瞬时值；I0(x)是零阶修正的贝塞尔函数．如果Z为常数，则a服从赖斯分布．但是受到阴影衰落的影响，Z是一个随机变量且服从Nakagami-m分布，即pZ(z)= 2mm/ (Γ(m)Ωmz2m-1) exp(-mz2/Ω)且z>0，其中m为Nakagami参数，Γ(x)为伽马函数．Ω=E[Z2]，表示直射分量的平均功率，显然Ω=S- 2b0．结合p(a|Z=z) 和pZ(z)可推出a的密度函数为[10]

p(a)=(a/b0) [2b0m/(2b0m+Ω)]mexp(-a2/(2b0))1F1m; 1;Ωa2/[2b0(2b0m+Ω)] ,(1)

其中，1F1(.;.;.)为合流超线几何函数．

和积译码器以信道输出的对数似然比为初始消息，即u0=2ya/σ2，在全零假设[5]下可得到u0的条件概率密度函数为Pu0(u0|a)= (σ2/ (8πa2))1/2exp[-(u0- 2a2/σ2)2/ (8a2/σ2)]．将其对a取平均，有

式(2)即为阴影-赖斯信道输出初始消息的概率密度函数．根据经历阴影的严重程度，信道可分为轻度阴影、中度阴影和重度阴影，相应的参数取值参见文献[10]中的Table Ⅲ．

2 对称性、稳定性与信道容量

2.1 对称性与稳定性条件

(3)

推导过程如下:

将式(2)代入参数s的定义式，可得

代入式(1)，有

(4)

至此，稳定性条件式(3)得证．

2.2 信道容量

已有很多文献论述了瑞利和赖斯衰落信道的香农限，但对于阴影-赖斯信道尚未见已出版文献报道，现推导如下．由信道容量定义，有

其中，I(W;Y，A)为W和Y的条件互信息，PW是W的概率分布，wi=±1且与a相互独立．由于阴影-赖斯信道是对称的，输入符号等概使互信息最大化，所以

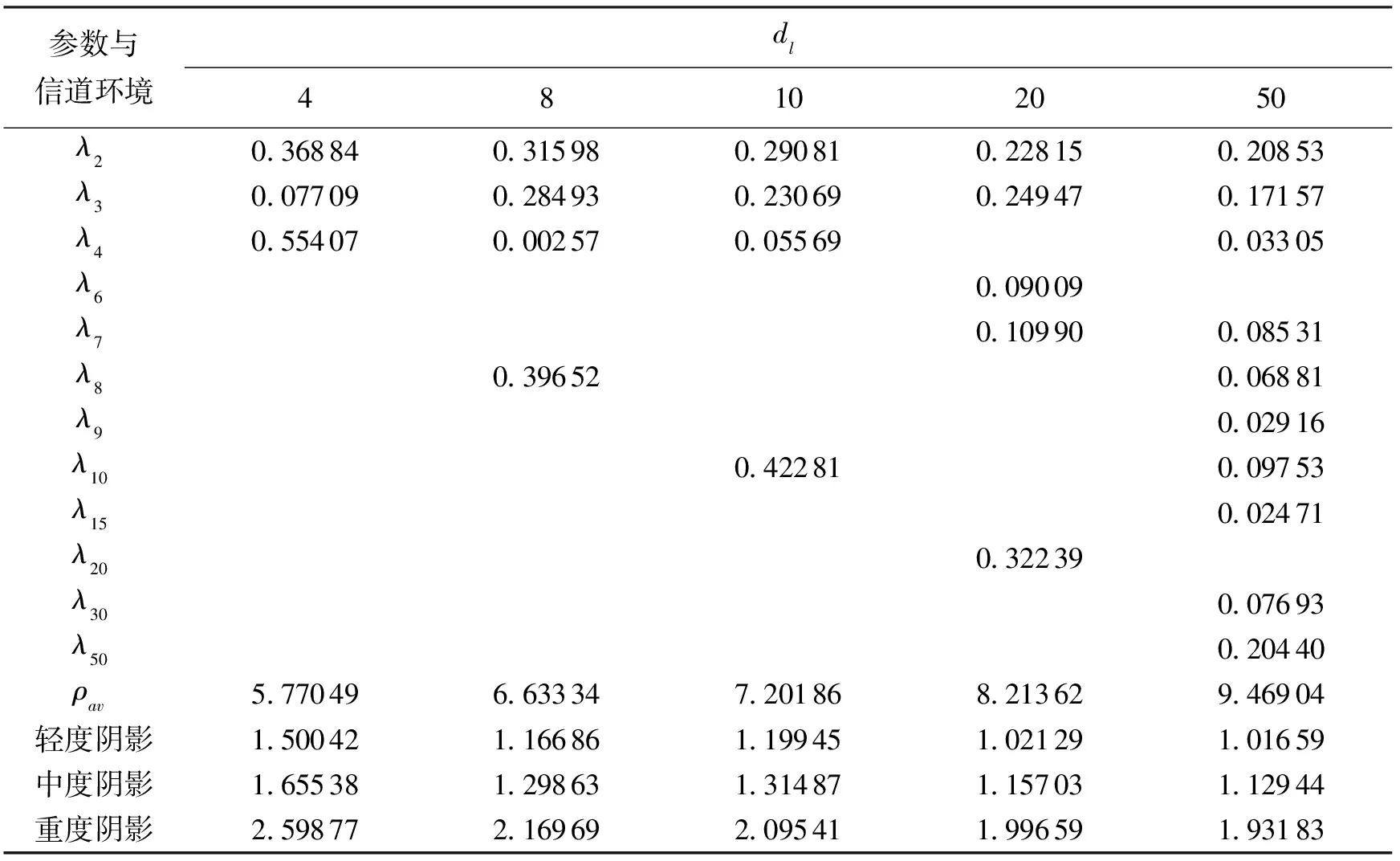
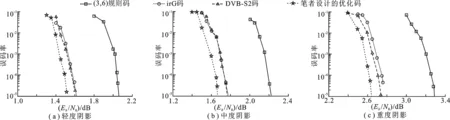
根据编码定理，存在码率R

表1不同环境下阴影-赖斯信道的香农限dB

信道环境R=2/3R=1/2R=1/3R=1/4轻度阴影2.09040.8383-0.1042-0.5098中度阴影2.31980.9783-0.0221-0.4507重度阴影3.66751.83110.4881-0.0803

3 数值计算与仿真

采用离散密度进化(Discretized Density Evolution，DDE)[7]来确定规则低密度奇偶检验码在阴影-赖斯信道中的译码门限，量化范围设为 [-25 ，25]，量化间隔为0.05．图1展示了 1/2 码率的(3，6)规则低密度奇偶检验码在不同阴影条件下阴影-赖斯信道中的门限，以及通过蒙特卡罗仿真获得的码长分别为105和106码字的误码率(Bit Error Rate， BER)性能．从图中可以看出，随着码长的增加，低密度奇偶检验码在误码率低于10-6时所需的信噪比收敛于译码门限，且码长为106时与门限的差距在 0.1 dB 以内．例如在重度阴影条件下，门限值约为 3.06 dB，而实际码字所需的信噪比约为 3.12 dB．这说明获取的门限值能够很好地预测低密度奇偶检验码在阴影-赖斯信道中的性能(界)．在轻度阴影下，系统性能最佳；中度阴影造成系统性能下降约 0.2 dB；在重度阴影下，系统性能下降约 1.2 dB．表2列出了几种常用的规则低密度奇偶检验码在阴影-赖斯信道中的译码门限和相应码率，其中(3，4)码的门限值和码率都最低，(3，9)码的最高，(3，6)码的适中．

图1 (3,6)规则低密度奇偶检验码在阴影-赖斯信道中的误码率与译码门限

通过比较表1和表2的结果可知，规则低密度奇偶检验码距离香农限还有一定距离 ． 例如(3，6)码在3种阴影环境中距离香农限约有 1.0～ 1.2 dB 的差距 ． 因此 ， 需要针对阴影-赖斯信道设计不规则码，这是一个连续空间参数(度分布)的非线性代价函数(门限值)最小化问题，而差分进化是一种非常高效的解决办法．其基本思想[6]简述如下: 在最大度数(dl，dr)和码率R确定的情况下，设参数L=dl+dr-5，并定义一个L维向量(λ3，…，λdl-1，ρ3，…，ρdr)，则该向量就完全确定了码字的度分布，且参数λ2，ρ2和λdl可由该向量计算得到，参见文献[6]中的式(25)和(26)．之后随机选择10L组向量作为“种子”，按照标准差分进化算法进行搜索，经过一定次数迭代后选择代价函数最小的那组度分布作为输出结果．在实际搜索过程中，为了降低计算复杂度，校验节点的度分布可限定为2个[7]，即取“集中度分布”ρ(x)= (1-ρ)xj-1+ρxj，且平均校验度数ρav= (1-ρ)j+ρ(j+ 1)=j+ρ．

表2不同码率的规则低密度奇偶检验码在阴影-赖斯信道中的译码门限dB

信道环境(3,9),R=2/3(3,6),R=1/2(4,6),R=1/3(3,4),R=1/4轻度阴影2.91591.87122.30011.3611中度阴影3.17982.03942.43631.4462重度阴影4.71333.05723.26601.9799

由于信道参数的不同，3种阴影环境下设计出的最佳不规则码度分布将有所差异，但是移动环境下信道状态会发生快速的随机变化且通信双方码字难以实时进行调整．因此，从实际出发使用最坏情况下得到的优化码字．从下面的结果可知该码字在另外两种环境下也具有良好的性能．设置环境为重度阴影后搜索得到的 1/2 码率不规则码度分布如表3所示．通过与表2的门限结果比较，相同环境下不规则码明显优于规则码．例如，3种阴影环境中变量节点最大度数 (dl=20) 的不规则码门限值比相应的(3，6)规则码分别低 0.85 dB，0.88 dB 和 1.06 dB．文献[5]在高斯信道中对低密度奇偶检验码进行了优化，将其中dl=20 的 1/2 码率不规则码记为irG并应用于阴影-赖斯信道，得到3种阴影下的译码门限分别为 1.029 96 dB，1.185 35 dB 和 2.119 21 dB．与表3的结果比较可知，在相同dl下获得的优化码门限更低，特别是在重度阴影下比irG码的门限低 0.12 dB．另外，当dl=50 时，得到的优化码字在3种阴影条件下的译码门限分别距离香农限约 0.18 dB，0.15 dB 和 0.10 dB．从上述结果来看，优化的不规则码在3种阴影下都具有良好的性能，但在重度阴影环境中相对规则码和irG码提升最大且最接近相应的香农限．这是因为进行搜索时已设置信道为重度阴影，若修改信道条件则会得到在该特定环境(中度或轻度阴影)中具有更优性能的码字．

达到或接近译码门限需要极长(例如大于106)的码字，这在实际应用中很难实现，因此需要考虑有限长度的低密度奇偶检验码．得到广泛应用的DVB-S2标准采用了码长64800的低密度奇偶检验码，因此笔者设置不规则码的码长为 64 800，其校验矩阵通过线性渐进边增长算法构造(环长较大)，且服从表3中dl=20 列的度分布．在构造校验矩阵的过程中，为了获得较大的最小码距和较好的“陷阱集”性能，选择具有最高连接度的校验节点[15]，而且可以基于平衡搜索树降低计算复杂度[16]．图2比较了优化的不规则码、DVB-S2采用的不规则码、irG码以及(3，6)规则码在3种阴影环境中的误码率性能．可以看出，在相同信道环境下，3种不规则码都远好于规则码，且笔者设计的优化码在3种阴影中的性能增益分别为 0.55 dB、0.59 dB 和 0.64 dB; irG与DVB-S2码字在中度阴影下的性能基本相当，在轻度和重度阴影下DVB-S2略好于irG码．笔者设计的不规则码性能优于DVB-S2码字: 在误码率达到10-5时，轻度阴影下所需的信噪比相对DVB-S2码字低 0.09 dB，中度阴影下差值为 0.11 dB，重度阴影下差值为 0.10 dB．

表3优化的1/2码率不规则低密度奇偶检验码度分布及译码门限dB

参数与信道环境dl48102050λ20.368840.315980.290810.228150.20853 λ30.077090.284930.230690.249470.17157λ40.554070.002570.055690.03305 λ60.09009λ70.109900.08531λ80.396520.06881λ90.02916λ100.422810.09753λ150.02471λ200.32239λ300.07693λ500.20440 ρav5.770496.633347.201868.213629.46904轻度阴影1.500421.166861.199451.021291.01659 中度阴影1.655381.298631.314871.157031.12944 重度阴影2.598772.169692.095411.996591.93183

图2 长度为64 800的低密度奇偶检验码性能比较

4 结 束 语

笔者对陆地移动卫星信道中的低密度奇偶检验码进行了性能分析和优化设计．首先证明了阴影-赖斯信道满足对称性条件，推导了稳定性条件和信道容量；在此基础上，利用密度进化工具计算出低密度奇偶检验码在该信道中的译码门限，能够快速评估码字在3种阴影环境中的性能(界)．基于差分进化对不规则低密度奇偶检验码的度分布进行了优化，在最大变量节点度数为50时译码门限距离香农限仅有约 0.1 dB；在码长为 64 800 且码率为 1/2 时，优化的不规则码相对规则码和DVB-S2不规则码有约 0.6 dB 和 0.1 dB 的性能增益．所以，笔者设计的优化码非常适合陆地移动卫星信道的信息传输．

[1] AL-SAEGH A M, SALI A, MANDEEP J S, et al. Channel Measurements, Characterization, and Modeling for Land Mobile Satellite Terminals in Tropical Regions at Ku-band [J]. IEEE Transactions on Vehicular Technology, 2017, 66(2): 897-911.

[2] LIU T, SUN B W, LI Z G, et al. Analysis of Channel Characteristics and Channel Model for Satellite Communication System[C]//Proceedings of the 2016 IEEE International Conference on Electronic Information and Communication Technology. Piscataway: IEEE, 2016: 166-169.

[3] ARTI M K. Channel Estimation and Detection in Hybrid Satellite-terrestrial Communication Systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(7): 5764-5771.

[4] LI J, LI Y B. Modeling Ka-band Satellite Communication System with MPSK[C]//Proceedings of the 2016 2nd IEEE International Conference on Computer and Communications. Piscataway: IEEE, 2016: 1785-1789.

[5] RICHARDSON T J, SHOKROLLAHI M A, URBANKE R L. Design of Capacity-approaching Irregular Low-density Parity-check Codes[J]. IEEE Transactions on Information Theory, 2001, 47(2): 619-637.

[6] HOU J, SIEGEL P H, MILSTEIN L B. Performance Analysis and Code Optimization of Low-density Parity-check Codes on Rayleigh Fading Channels[J]. IEEE Journal on Selected Areas in Communications, 2001, 19(5): 924-934.

[7] 徐华, 徐澄圻. Rice信道下LDPC码密度进化的研究[J]. 电子与信息学报, 2006, 28(10): 1831-1836.

XU Hua, XU Chengqi. Research of Density Evolution of LDPC Codes over Rice Channels[J]. Journal of Electronics & Information Technology, 2006, 28(10): 1831-1836.

[8] TAN B S, LI K H, TEH K C. Performance Analysis of LDPC Codes with Maximum-ratio Combining Cascaded with Selection Combining over Nakagami-mFading[J]. IEEE Transactions on Wireless Communications, 2011, 10(6): 1886-1894.

[9] LUTZ E. Modelling of the Land Mobile Satellite Communications Channel[C]//Proceedings of the 2013 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications. Piscataway: IEEE, 2013: 199-202.

[10] ABDI A, LAU W C, ALOUINI M S, et al. A New Simple Model for Land Mobile Satellite Channels: First- and Second-order Statistics[J]. IEEE Transactions on Wireless Communications, 2003, 2(3): 519-528.

[11] BAE H, KIM H, BAE K. Analysis of Noise Threshold of Regular LDPC Codes on LEO Satellite Channel [C]//Proceedings of the 2008 23rd International Technical Conference on Circuits/Systems, Computers and Commnications. Piscataway: IEEE, 2008: 1289-1292.

[12] ARTI M K. Performance Evaluation of Maximal Ratio Combining in Shadowed-Rician Fading Land Mobile Satellite Channels with Estimated Channel Gains[J]. IET Communications, 2015, 9(16): 2013-2022.

[13] ARTI M K, JINDAL S K. OSTBC Transmission in Shadowed-Rician Land Mobile Satellite Links[J]. IEEE Transactions on Vehicular Technology, 2016, 65(7): 5771-5777.

[14] DAI C Q, HUANG N N, CHEN Q B. Adaptive Transmission Scheme in Ka-band Satellite Communications[C]//Proceedings of the 2017 International Conference on Digital Signal Processing. Piscataway: IEEE, 2017: 336-340.

[15] XIAO H, BANIHASHEMI A H. Improved Progressive-edge-growth(PEG) Construction of Irregular LDPC Codes[J]. IEEE Communications Letters, 2004, 8(12): 715-717.

[16] 陈霖，冯大政. 一种快速的渐进边增长算法[J]. 西安电子科技大学学报. 2009, 36(3): 406-409.

CHEN Lin, FENG Dazheng. Fast Progressive Edge-growth Algorithm [J]. Journal of Xidian University, 2009, 36(3): 406-409.