采用OFDM-LFM的MIMO雷达高速目标波形设计
2018-06-14李升远张馨恬唐世阳
李升远, 张馨恬, 唐世阳
(1. 西安电子科技大学 雷达信号处理国家重点实验室,陕西 西安 710071;2. 西北工业大学 明德学院,陕西 西安 710124)
随着临近空间高超声速飞行器的发展,飞行器的速度越来越快,速度一般超过5倍音速,且具有较强的机动性,雷达散射截面积较常规目标大大降低,这对雷达目标检测技术提出了新的挑战[1-3]. 长时间积累是改善雷达的检测性能的重要手段,但在较长的积累时间内,由于飞行器高速运行,目标容易出现跨波束现象, 而相控阵雷达等的工作方式则限制了对跨波束走动的研究. 当目标在发射端照射时间内出现跨波束走动时,相控阵雷达等无法对其进行补偿[4]. 单基地多输入多输出(Multiple-Input Multiple-Output,MIMO)雷达使用正交信号,发射信号在空域形成一个低增益的宽波束,覆盖整个需要监测的范围[5-6]. 即使目标出现了跨波束走动,单基地MIMO雷达仍然能够接收到所有的回波,不会有能量的损失,这为后续信号处理提供了保障.
单基地MIMO雷达采用的发射波形主要有正交频分复用线性调频信号(Orthogonal Frequency Division Multiplexing-Linear Frequency Modulation,OFDM-LFM)、正交多相编码信号和正交离散频率编码信号. 其中编码信号对目标速度的容忍范围较低,只能应用于较低多普勒频移的情况[7-10].对于高速目标而言,其性能将大大降低. OFDM-LFM作为MIMO雷达的发射波形时,每个子载频通过不同的通道并行发射,每个信号占有不同的频带,通过接收信号处理,可以分离出各个发射通道的信号[11-12]. 由于每个子载频调制的是线性调频信号,OFDM-LFM波形在高超声速背景下,有较好的应用前景,但当子载频间频率间隔较大时,会对接收端通道间的相参性产生影响. 文献[13]通过载频间的非均匀选取,在空域上获得了良好的相关性能. 文献[14]中提出了一种分时同载频、同带宽的OFDM-LFM波形设计方法,并将其应用于合成孔径成像. 以上两种方法都提升了接收端回波的相关性,然而为了降低距离旁瓣获得更好的相关性能,多普勒容忍性都有所不足,无法满足高速目标的应用场景.
针对上述问题,文中提出一种新的OFDM-LFM波形设计方法.该方法通过发射端分时发射各子载频,接收端合成处理,实现了各通道信号的分离,且各通道信号具有相同载频、带宽. 因此,较传统OFDM-LFM信号而言,文中提出的波形具有更好的相参性能,同时,文中提出的方法,由于载频间隔连续,在接收端合成后,匹配滤波性能与单载频LFM的相似,高速目标回波下脉压性能损失较小. 最后,通过仿真实验验证了文中方法的有效性.
1 波形设计
1.1 子载频信号模型
若单基地MIMO雷达发射通道数为M,令子载频个数等于发射通道数,则第m个子载波信号为
(1)
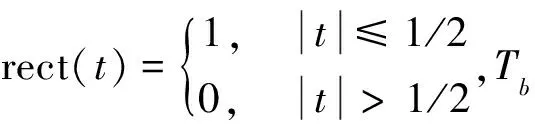
(2)
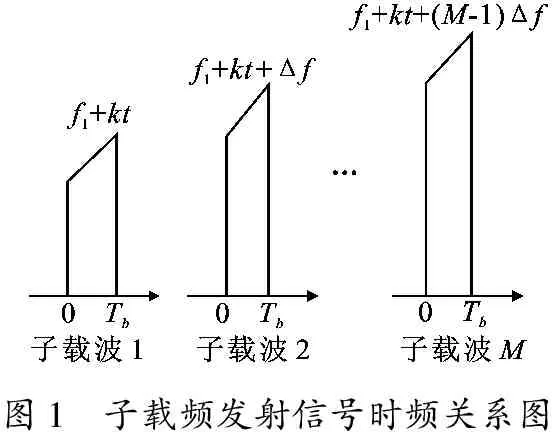
图1 子载频发射信号时频关系图
在式(2)条件下,子载频间的频差应为Δfn,m=fn-fm=pTb,p=1,2,…, 其中p为任意正整数,且各子载波所占频段不重合,即 (Bm+Bm+1)/2≤ Δfm,m+1,Bm为第m个子载波的带宽.
当相邻子载频频率间隔一定,且调频斜率相等时,子载波信号的时频关系如图1所示.
1.2 调制矩阵设计
根据上一小节给出的子载波信号模型,这里定义子载频矩阵Φ为
(3)
依据矩阵Φ,调制后的第m个发射通道的发射信号矩阵可表示为
xm=Rm⊙Φ,(4)
其中,⊙表示Hadamard积,Rm为第m个发射通道的调制矩阵,Rm是一个M×M的矩阵,每一行和每一列有且只有一个非零元素,且非零元素为1. 0代表其对应位置的子载频没有被使用,1代表对应子载频被使用了. 这里Rm被定义为
(5)
其中,diag(R,n)表示取矩阵R的第n条主对角线为1的列,1表示元素全为1的列向量,由上式可以看出,R1仅有主对角线元素不为0,R2仅有第1对角线及第 -3 对角线元素不为0,以此类推.对于第m个通道而言,一个脉宽由M个长度为Tb的子脉宽组成,在每一个子脉宽内,只发射一个子载频,由发射信号矩阵xm可以得到第m个发射通道发射信号为
ym=sum(xm(:,:)) ,(6)
其中,sum(:,:)表示将矩阵中所有元素加和.
由信号矩阵可知,在相同时间内,不同通道占用不同的子载波,而总时间段内发射信号带宽相同. 如图2给出了3种6个发射通道的OFDM-LFM信号示意图,可以看到,每个Tb时间段内,每个通道发射不同的子载频,而同一时间内各个通道占用不同的频段,从而达到相同时间通道分离的目的.
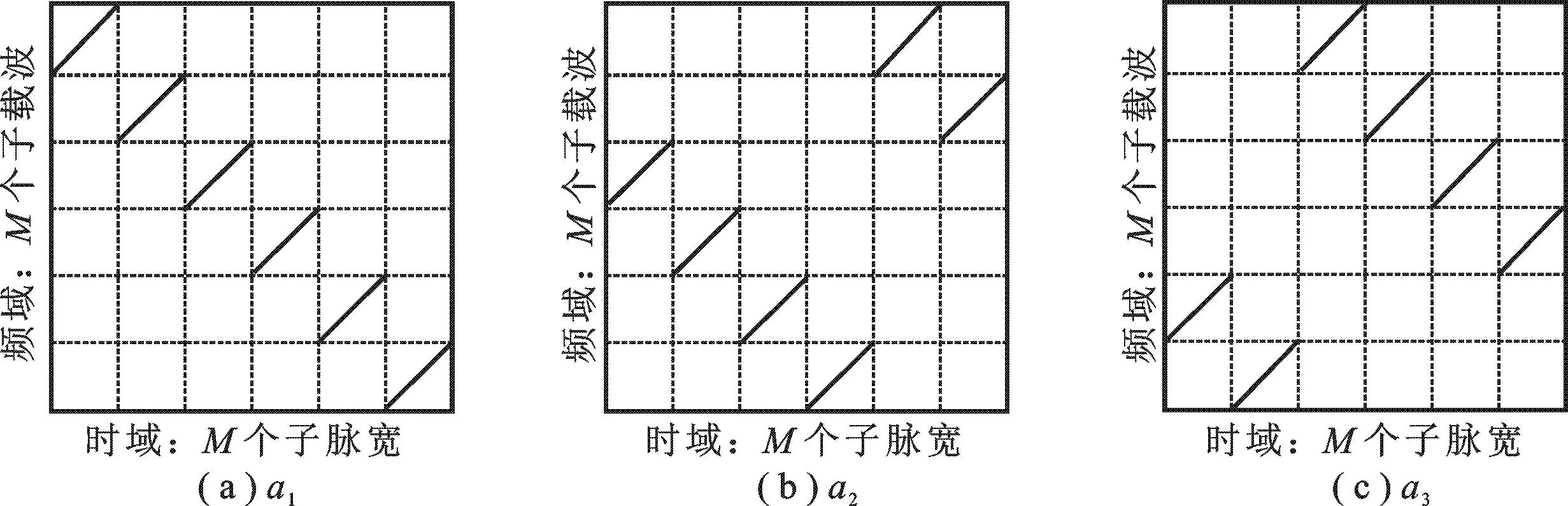
图2 3种发射信号示意图
2 接收信号分离与合成
上一节介绍了文中提出的波形设计方法,本节给出相应的接收端信号分离处理算法.对于单个脉冲回波,为了叙述简便,省略幅度信息,若接收通道数为N,则下变频后第n个接收通道的回波为
(7)
其中,c为光速,fc发射载频,fd=2v0λc,为目标多普勒频率,v0为目标速度,λc为载频波长,τm,t和τn,t为对应通道的发射、接收延时.
将回波在时域上按Tb间隔划分为M个子信号,则第n个接收通道第i个子脉宽信号为
(8)

图3 接收端带宽合成原理图
将每个子脉宽信号转换到频域,把各个发射通道对应的频带截取出来,然后将各子脉宽内相同发射通道截取的信号进行相加. 至此,接收端在频域完成对不同发射通道信号的分离与合成,处理原理如图3所示.对于每一组发射波形,不同子脉宽内不同的频带在接收端被合成为一个带宽叠加信号,带宽变为原子载频的M倍,而脉宽则变为原来信号的 1/M.从而实现了相同载频下,相同带宽的波形设计.
可以看到,文中波形设计对应的接收端处理较传统匹配滤波的波形分离方法有所不同.文中方法通过子脉宽的划分,之后频域对应通道频带截取,不同子脉宽频带拼接,从而得到不同通道完整的发射信号的回波, 得到回波后可再进行匹配滤波等后续操作. 该处理方式并不要求整体信号间的隔离度,仅需要子脉宽内各通道所发射子载频间具有较高的隔离度,而各通道发射信号在脉宽内频率顺序变化近似于单个线性调频(Linear Frequency Modulated,LFM)信号,从而保证较好的多普勒容忍性,满足高速目标背景需求. 同时,由于目标回波子载频调制顺序与角度无关,且文中提出的接收端分离与合成方法不涉及空域信息,所以该方法同样适用于多目标情况.
3 仿真实验
为验证文中的OFDM-LFM波形设计方法,对子载波间的自相关及互相关特性、高速目标回波脉压主副比进行了仿真实验. 仿真实验参数设置如下: 设系统由M=6 个发射阵元组成,载频fc= 1 GHz,子脉宽Tb= 20 μs,总脉宽为 120 μs,频率间隔 Δf= 1 MHz,则调频斜率k= 5× 1010,根据给出参数,接收端合成的信号带宽Br= 6 MHz.下变频后回波采样频率fs= 2Br.
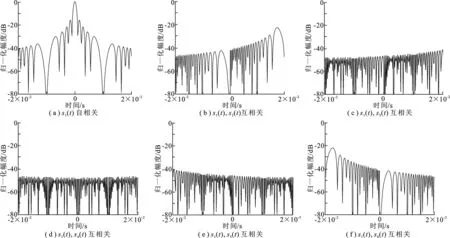
图4 子载频s1(t)自相关及互相关曲线
由于接收端按子脉宽频域分离各通道信号,这就要求子载频间需要有较高的通道隔离度,子载频s1(t)自相关及s1(t)与其他载频的互相关曲线如图4所示. 由图4可以看出,s1(t)的自相关峰值远高于互相关峰值,且互相关峰值最高处不超过 -20 dB, 这说明子载频间具有较好的隔离度.当回波带有多普勒频移时,同样时间内不同子载频多普勒频移相同,因此,并不改变互相关性质. 所以,接收端每个子脉宽内的信号分离处理具有高速容忍性.
图5给出了不同速度下,不同MIMO雷达波形脉压结果图.图5(a)为文献[14]给出的波形脉压图,其调制矩阵Ra为
(9)
图5(b)~图5(c)分别为相同脉宽,脉压增益下的随机二项码信号和正交离散频率编码脉压结果图,图5(d)~图5(f)为文中提出波形在接收端拼接处理后对应图2中3种波形下的脉压结果.由图5(a)可以看出,文献[14]中的波形脉压后能量在高速区时域发生了能量扩散,性能显著降低,而由图5(b)和图5(c)可得,相位编码信号和正交离散频率编码脉压结果只能在较低速区域实现能量聚积,并不适用于高速目标. 由图5(d)~图5(f)可以看出,文中提出波形在高速目标下匹配滤波性能接近,与其他两种波形相比,脉压能量损失最小,可以实现能量的聚集,但随着速度变化,脉压峰值在时间上会有一定的偏移,不同通道峰值相对偏移量相同,因此,并不影响后续处理.
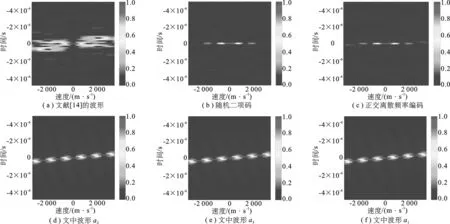
图5 不同速度下的波形脉压图
4 结 束 语
相控阵等雷达的工作体制限制了其对高速目标跨发射波束情况下的检测性能,MIMO雷达宽发射波束的特性能有效解决这一问题,然后现有单基地MIMO雷达波形对速度容忍性较差. 针对这一问题,文中给出了一种适用于高速目标的MIMO雷达OFDM-LFM信号的波形设计方法,并对接收端的信号分离及合成进行了研究,其核心思想是利用LFM信号相邻频带间具有的低互相关特性,通过多路信号同时不同频带,分时发射一样的带宽信号,从而在接收端得到带宽相同的多路信号.文中给出的波形设计方法较原有算法,更加适用于高速目标检测背景,仿真实验说明了该方法接收端子脉冲内信号分离的可行性,并且验证了基于设计波形能有效减少高速目标多普勒频移所带来的脉压损失,为MIMO雷达在高速目标检测中的应用提供了思路.
[1] 汪连栋, 曾勇虎, 高磊, 等. 临近空间高超声速目标雷达探测技术现状与趋势[J]. 信号处理, 2014, 30(1): 72-85.
WANG Liandong, ZENG Yonghu, GAO Lei, et al. Technology Status and Development Trend for Radar Detection of Hypersonic Target in Near Space[J]. Journal of Signal Processing, 2014, 30(1): 72-85.
[2] 肖松, 谭贤四, 李志淮, 等. 雷达探测临近空间高超声速目标性能需求分析[J]. 现代防御技术, 2013, 41(5): 87-92.
XIAO Song, TAN Xiansi, LI Zhihuai, et al. Analysis of Detection Performance Requirement on Radar for Near-space Hypersonic Target[J]. Modern Defence Technology, 2013, 41(5): 87-92.
[3] 肖松, 谭贤四, 王红, 等. 地基雷达部署对探测临近空间高超声速目标影响研究[J]. 电子与信息学报, 2015, 37(7): 1723-1728.
XIAO Song, TAN Xiansi, WANG Hong, et al. Detection Performance Assessment of Near-space Hypersonic Target Based on Ground-based Radar[J]. Journal of Electronics & Information Technology, 2015, 37(7): 1723-1728.
[4] 骆成, 李军, 何子述, 等. 高速运动平台MIMO雷达“三跨”补偿研究[J]. 电子科技大学学报, 2014, 43(1): 36-41.
LUO Cheng, LI Jun, HE Zishu, et al. Study of “Three Crossing” Compensations of High Speed Moving MIMO Radar[J]. Journal of University of Electronic Science and Technology of China, 2014, 43(1): 36-41.
[5] 王玉玺, 黄国策, 李伟, 等. 杂波和有色噪声条件下MIMO 雷达波形设计[J]. 西安电子科技大学学报, 2017, 44(4): 125-131.
WANG Yuxi, HUANG Guoce, LI Wei, et al. MIMO Radar Waveform Design in the Presence of Clutter and Colored Noise[J]. Journal of Xidian University, 2017, 44(4): 125-131.
[6] ZHANG W, VOROBYOV S A. Joint Robust Transmit/Receive Adaptive Beamforming for MIMO Radar Using Probability-constrained Optimization[J]. IEEE Signal Processing Letters, 2016, 23(1): 112-116.
[7] DENG H, GENG Z, HIMED B. MIMO Radar Waveform Design for Transmit Beamforming and Orthogonality[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(3): 1421-1433.
[8] CUI G, YU X, PIEZZO M, et al. Constant Modulus Sequence Set Design with Good Correlation Properties[J]. Signal Processing, 2017, 139: 75-85.
[9] 赵宜楠, 张涛, 李风从, 等. 基于交替投影的MIMO雷达最优波形设计[J]. 电子与信息学报, 2014, 36(6): 1368-1373.
ZHAO Yi’nan, ZHANG Tao, LI Fengcong, et al. Optimal Waveform Design for MIMO Radar via Alternating Projection[J]. Journal of Electronics & Information Technology, 2014, 36(6): 1368-1373.
[10] 杜晓林, 苏涛, 王旭, 等. 基于Golay互补序列空时编码的MIMO雷达波形设计[J]. 电子与信息学报, 2014, 36(8): 1966-1971.
DU Xiaolin, SU Tao, WANG Xu, et al. Golay Complementary Sequence with Space Time Coding for MIMO Radar Waveform Design[J]. Journal of Electronics & Information Technology, 2014, 36(8): 1966-1971.
[11] 刘波, 韩春林, 苗江宏. MIMO雷达正交频分LFM信号设计及性能分析[J], 电子科技大学学报, 2009, 38(1): 28-31.
LIU Bo, HAN Chunlin, MIAO Jianghong. OFD-LFM Signal Design and Performance Analysis for MIMO Radar[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(1): 28-31.
[12] 陈正辉, 严济鸿, 何子述. MIMO雷达OFDM-LFM波形设计与实现[J]. 雷达科学与技术, 2013, 11(1): 77-86.
CHEN Zhenghui, YAN Jihong, HE Zishu. Design for MIMO Radar and Implementation of OFDM-LFM Waveform[J]. Radar Science and Tchnology, 2013, 11(1): 77-86.
[13] 李慧, 赵永波, 冯大政, 等. 非均匀间隔OFD-LFM的MIMO雷达波形设计[J], 电子与信息学报, 2016, 38(4): 927-933.
LI Hui, ZHAO Yongbo, FENG Dazheng, et al. MIMO Radar Waveform Design for OFD-LFM with Various Frequency Steps[J]. Journal of Electronics & Information Technology, 2016, 38(4): 927-933.
[14] WANG W Q. MIMO SAR OFDM Chirp Waveform Diversity Design with Random Matrix Modulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1615-1625.
