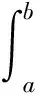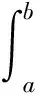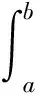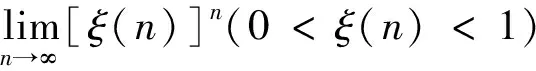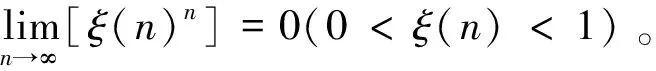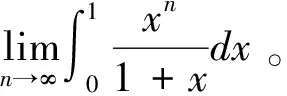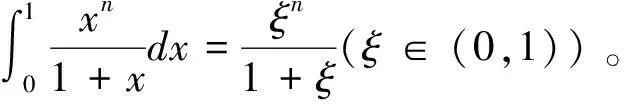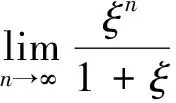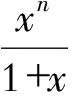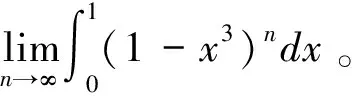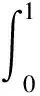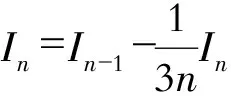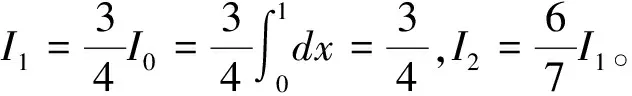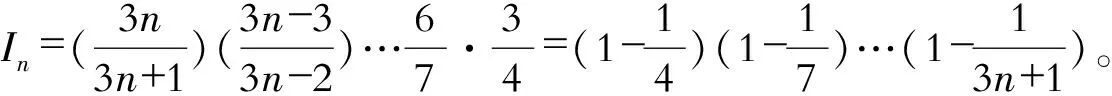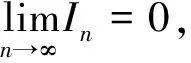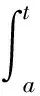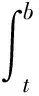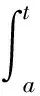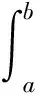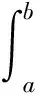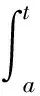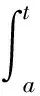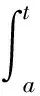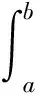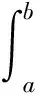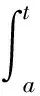现行高等数学教材中的积分中值定理应该强化

2018-06-14，

天津职业院校联合学报 2018年5期

关键词：莱布尼茨微积分牛顿

，

(天津冶金职业技术学院，天津 300400)

在文献(6)中，本文作者简论了高等数学(微积分、数学分析)教材改革的必要性和原则，下面谈谈我们对积分中值定理所作的研究。

众所周知，积分中值定理在解决原函数不易求的积分和处理抽象函数的积分以及进行理论探讨时是十分重要的。

现行高等数学(微积分、数学分析)教材中，关于积分中值定理都是如下叙述的：

这样叙述的积分中值定理不仅与微分中值定理不统一(ξ的存在区间)，而且用这样叙述的积分中值定理解答某些题目时，还会增加不小的难度(参见例1—例3)。因此应该将现行高等数学(微积分、数学分析)教材中的积分中值定理加强为：

在文献(2)中，作为一个例题，利用牛顿——莱布尼兹公式证明了强化的积分中值定理。但是，在现行高等数学(微积分、数学分析)教材中，关于牛顿——莱布尼兹公式的证明都用了微积分基本定理(原函数存在定理)，而现行高等数学(微积分、数学分析)教材中，微积分基本定理的证明又都用了积分中值定理，这就有循环论证之嫌。

下面不用微积分基本定理而直接证明强化的积分中值定理。与此同时，将现行高等数学(微积分、数学分析)教材中的定积分的保号性、定积分比较定理、定积分的估值不等式都予以了强化。强化的定积分的保号性、定积分比较定理、定积分的估值不等式表明了，现行高等数学(微积分、数学分析)教材中的定积分的保号性、定积分比较定理、定积分的估值不等式中的等号在什么情形下可以去掉，这对于某些题目的解答是方便的。

在下面的讨论中，如无特殊说明，假定所遇到的函数、在闭区间上是可积的。下面出现的定理或推论只证明现行高等数学(微积分、数学分析)教材没有的。

定理1 若在闭区间[a,b]上函数f(x)0，则f(x)dx0。

推论1 若在闭区间[a,b]上函数f(x)g(x)，则f(x)dxg(x)dx。

推论2 若在闭区间[a,b]上连续函数f(x)0，且f(x)不恒等于0，则f(x)dx>0。

证因为在闭区间[a,b]上连续函数f(x)不恒等于0，所以至少存在一点x0∈[a,b]，使f(x0)>0。

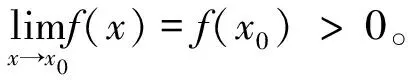
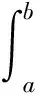
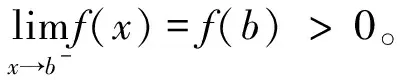
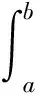
定理1和推论2称为定积分的保号性。

推论3 若在闭区间[a,b]上连续函数f(x)g(x)，且f(x)不恒等于g(x)，则f(x)dx>g(x)dx.

证因为在闭区间[a,b]上连续函数f(x)g(x)，且f(x)不恒等于g(x)，所以在闭区间[a,b]上函数f(x)-g(x)0，且f(x)-g(x)不恒等于0，进而由推论2得[f(x)-g(x)]dx>0，从而有f(x)dx-g(x)dx>0，移项得f(x)dx>g(x)dx.

推论1和推论3称为定积分比较定理。

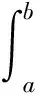
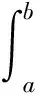
其中m和M分别是函数f(x)在闭区间[a,b]上的最小值和最大值。

证因为函数f(x)在闭区间[a,b]上连续，所以由最值定理知，函数f(x)在闭区间[a,b]上有最小值m和最大值M，且m⪯f(x)⪯M(x∈[a.b])。

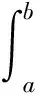
式(1)和式(2)称为定积分的估值不等式。它表明当定积分不能用或不宜用牛顿——莱布尼茨公式求其值时，可以用被积函数在积分区间上的最大值和最小值来估计该定积分的值。

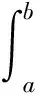
证因为函数f(x)在闭区间[a,b]上连续，所以由最值定理知，存在x1,x2∈[a,b]使f(x1)=m、f(x2)=M分别是函数f(x)在闭区间[a,b]上的最大值和最小值，且m⪯f(x)⪯M(x∈[a,b]).

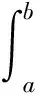
若M-m>0，则函数f(x)在闭区间[a,b]上不恒为常数，由介值定理知在开区间(a,b)内至少存在一点θ，使m

需要指出的是：除了按上面的途径证明强化的积分中值定理外，还可以按下面的两条途径之一证明强化的积分中值定理(参见文献(5))。

途径一：先用定积分定义和拉格朗日中值定理证明牛顿—莱布尼茨公式，再用牛顿—莱布尼茨公式强化的积分中值定理。

途径二：先用导数定义和极限定义(ε-δ)证明微积分基本定理(原函数存在定理)，再用微积分基本定理证明牛顿—莱布尼茨公式，最后用牛顿—莱布尼茨公式强化的积分中值定理。

下面说明微分中值定理(拉格朗日中值定理)与积分中值定理的联系：

因为函数F(x)在闭区间[a,b]上满足拉格朗日中值定理的条件，所以由拉格朗日中值定理，知至少存在一点ξ∈(a,b)，使F(b)-F(a)=F′(ξ)(b-a)=f(ξ)(b-a).

综上，可以看出微分中值定理(拉格朗日中值定理)与积分中值定理的联系：对函数F(x)而言，它们是同一事物的不同表现.牛顿——莱布尼茨公式在微分与积分之间起了一种桥梁的作用，将微分与积分沟通了，使微分与积分成为一个有机的整体，因此牛顿——莱布尼茨公式被称为微积分基本公式。

与拉格朗日中值定理一样，在积分中值定理中，一般不知道ξ的确切位置，而仅知道ξ的存在性(ξ∈(a,b))，对ξ的确切位置未作任何断言。ξ一般与被积函数和积分区间有关。

当极限变量n出现在被积函数中时，随着n的不同，被积函数也不同，进而ξ在开区间(a,b)内的位置也不同，从而ξ是n的函数，ξ应该记为ξ(n)。

显然文献(3)中所给出的正确解法比用强化的积分中值定理的解法，不仅所用的知识点多，而且计算量大。

以上解法在文献(4)中被认为是错误的。文献(4)中所给出的错误理由是：记错了积分中值定理，积分中值定理中的ξ可以取积分上限、下限处的值。本题的ξ∈[0，1]，在没有证明ξ≠0的情况下，本题取极限所推出的结果是不可信的，并给出下面的正确解法。

显然文献(4)中所给出的正确解法不仅所用的知识点多，而且计算量大，比用强化的积分中值定理的解法既繁且难。

例3 设函数f(x)在闭区间[a,b]上连续，在开区间(a,b)内可导且f′(x)>0。证明在开区间(a,b)内存在唯一的ξ，使曲线y=f(x)与两直线y=f(ξ)、x=a所围成的平面图形的面积S1是曲线y=f(x)与两直线y=f(ξ)、x=a所围成的平面图形的面积S1是曲线y=f(x)与两直线y=f(ξ)、x=b所围成的平面图形的面积S2的3倍。

这是一道全国统考的考研题，原解答如下：

证在闭区间上任取一点t，则