基于粒子群算法和粗糙集的特征选择方法

杨祺 王谦

(南京熊猫汉达科技有限公司制造部,江苏南京 210014)

1 引言

特征选择也叫特征子集选择,是选取一系列的特征构成一个特征子集,能够使得这个子集具有与特征全集相同或者更好的功能,特别是对于数据的分类。特征选择算法是提高学习算法性能的一个重要手段,是模式识别中数据预处理的关键步骤[1]。在以往的数据分类过程中,数据集通常会包含大量的无关和冗余特征,导致维数的复杂度较高,造成一定的维数灾难,尤其是增加了分类的负担。特征选择算法的出现为此提供了一种行之有效的解决方式[2]。

粗糙集可以处理具有不确定性和模糊性的数据,用于发现不一致数据中的模式。粗糙集已在模式识别中作为一种有用的特征选择方法。基于粗糙集的特征选择的优化准则是找到最短的或最小约简的同时获得高质量的分类,而目前尚无最佳的属性约简算法[3]。一般来说,基于粗糙集的特征选择方法,主要以贪婪算法为主。贪婪算法通常采用粗糙集属性重要性作为启发式知识,以空集或属性核开始,然后采用前向选择或向后消除的方式。前向选择是从空集开始,逐一增加,从候选集中选择重要的属性,直到选定的集合是一个约简集合。向后消除则从完整属性集开始,并逐步移除属性,从而获得约简集。基于贪婪算法的粗糙集特征选择,能够获得一定的属性约简,但是效率低下,不能保证所选特征的质量,同时造成一定的资源浪费。

特征选择方法的划分一般是根据评价函数的不同,大致可以分为封装模式和过滤模式。过滤模式通过分析特征子集内部的特点来衡量其好坏,一般用作预处理。封装模式实质上是一个分类器,用选取的特征子集对样本集进行分类,分类的精度作为衡量特征子集好坏的标准。在封装模式中,分类学习算法封装在特征选择的过程中,以学习算法的性能作为子集的评价标准。当满足一定条件(一般设定的迭代次数)时将最优的特征子集输出,同时获得一个具有较高分类性能的模型。在封装模式的特征选择方法中,可以采用多种学习算法来评价特征子集,如贝叶斯分类器、邻近算法、支持向量机及神经网络等。特征选择实际是一个组合优化问题,特征选择过程中,往往特征数目繁多,搜索空间较大,所以需要搜索算法去获得最优的选择方案,存在的搜索方法有序列前向选择SFS和序列后向选择SBS、粒子群算法(PSO)、蚁群算法(ASO)等。本文采用封装模式的特征选择方法,将粗糙集作为评价函数,以骨干粒子群算法(Bare bones PSO)作为搜索算法,通过实验说明提出算法的有效性和实用性。

2 粒子群算法

2.1 传统粒子群算法

粒子群算法是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法[4]。其描述如下:

假设在一个D维的目标搜索空间, m个粒子组构成一个群落,其中的第 i个粒子,表示一个D维的向量 Xi=(xi1, xi2....xiD),i = (1,2,3....m)。其中第 i个粒子在目标搜索空间的位置是 xi。每一个粒子所在的位置就是一个潜在的备选解,将 xi代入到目标函数中,计算其适应度值。每个粒子 i还有一个速度决定其飞翔的方向和距离,Vi=(vi1,vi2...viD)速度也是一个D维的向量。第 i粒子搜索到的最优位置记为 Popt(局部最优解),整个粒子群迄今为止搜索到的最佳位置记为 Gopt(全局最优解)。粒子速度和位置的更新公式如下:

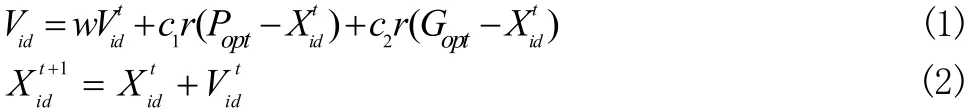
其中, d = 1 ,2,3...D, i = 1 ,2,3...m 。 m是种群的规模; c1和c2加速常数,r是[0,1]之间任意的随机数,t是迭代次数。上述的粒子群算法,只适应于连续问题的求解。Kennedy和Eberhar提出了离散二进制粒子群算法(BPSO)[5],这种算法采用的是二进制的编码形式。在二进制的粒子群算法中,粒子的位置 Xi(10110011)采用二进制的字符串表示,而速度向量则不做此要求。粒子的位置更新公式变为:

2.2 骨干粒子群算法

Kennedy在原始的粒子群算法的基础之上提出了Bare bones粒子群算法[6]。这种算法舍弃粒子的速度,采用高斯模型,利用粒子的局部的全局最优解来跟新粒子的位置,公式如下:

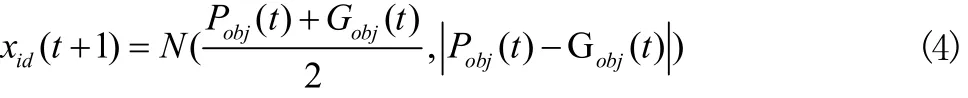
Pobj(t)代表局部最优解, Gobj(t)代表全局最优解。在上述公式中,粒子的位置被表示为局部和全局最优解的均值和偏差的高斯分布。为了解决粒子群收敛于局部最优解的问题,需从优化算法全局探索能力和局部开发能力两方面入手。粒子需要能够跳出当前局部最优位置,并提高当前邻域内细化搜索的能力。骨干粒子群算法的提出很好的解决了这一问题,同时保持了粒子多样性和收敛之间的平衡,同时骨干粒子群算法参数较少,具有很高的应用性。

在粒子群的初始化中将引入混沌模型,种群初始化采用随机方式,即 xid= r 。混沌模型的初始化进程为:

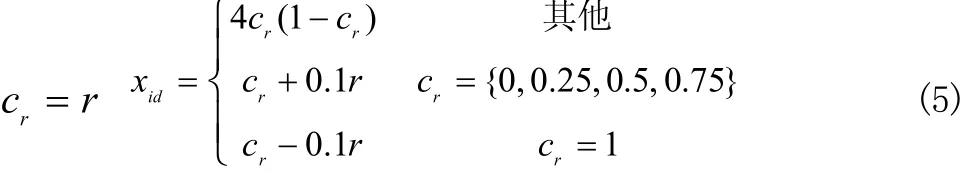
在离散粒子群算法的特征选择中,粒子的位置向量Xi=(xi1, xi2...xiD)代表一个特征子集,其中的 xi1就代表一个特征。在离散粒子群算法中 xi1是二进制,当 xi1取0时,表示这个特征没有被选中,当 xi1为1的时候则表示该特征被选中。例如, Xi=(01000111)表示该特征子集中有8个特征,1的个数为4,表示4个特征被选中。传统的特征选择算法中,都是采用离散粒子群算法,通过Sigmoid函数将粒子的位置向量由十进制转换为二进制,但是在骨干粒子群算法中,粒子的速度向量被舍弃,无法使用Sigmoid函数。因此需要引入解码机制,将特征被选入特征子集的可能性作为解码的原理,把粒子群中的粒子作为解决问题的一个潜在方法。粒子Xi=(xi1,xi2...xiD),xi1∈ [ 0,1]表示第一个特征被选择的可能性:

当 eij= 1时,表示第j个特征被选入特征子集。如果为0,则表示该特征未被选入。在统计被选入的特征数目时,可直接统计 eij中的1的个数。

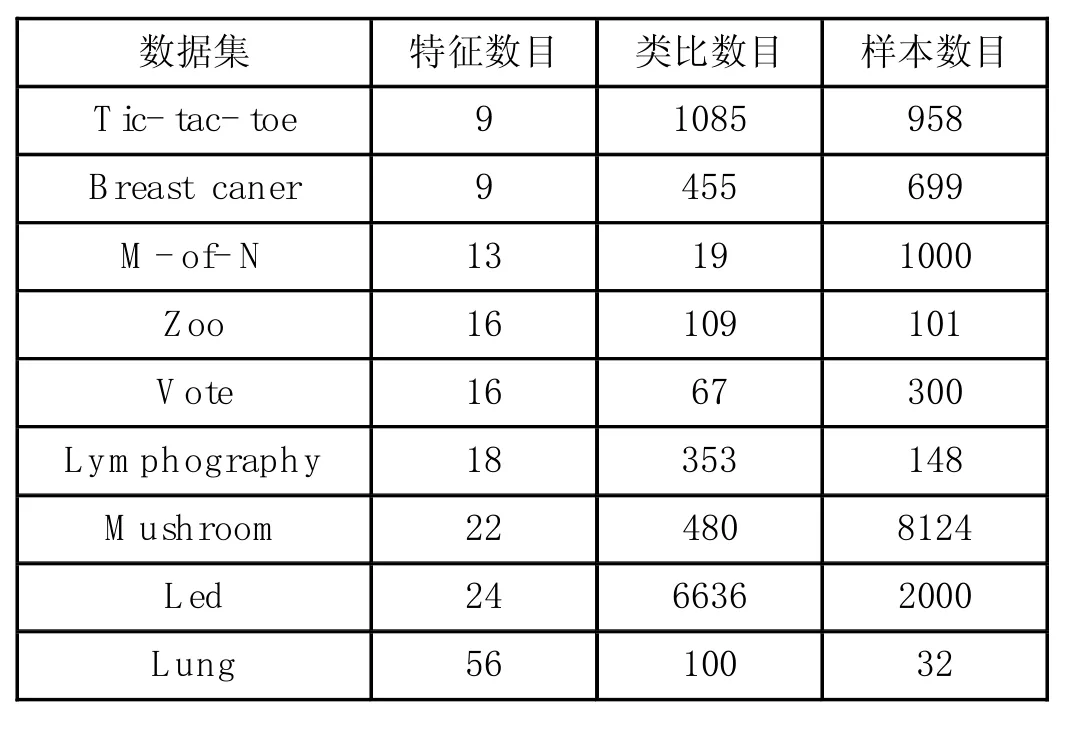
表1 实验数据

3 粗糙集

粗糙集理论是Pawlak在1982年提出的一种能够定量分析处理不精确或者不完整信息的新型数学工具。粗糙集理论最初的原型来源于简单的信息模型,通过关系数据库分类归纳形成概念和规则,在保持分类能力不变的前提下,通过等价关系的分类以及对于目标的近似来实现,由于粗糙集理论思想新颖、方法独特,已成为一种重要的智能信息处理技术,该理论已经在机器学习等方面得到了广泛应用。特征选择中存在的数据往往是不准确的、冗余的,而粗糙集是一个强大的数据分析工具,它能够表达和处理不完备信息,能在保留关键信息的前提下对数据进行简化并求得数据的最小表达式,识别并评估数据之间的依赖关系,揭示出数据的简单模式。一个信息表数据表达系统表示为 S = ( U,A),U是样本的集合, A是有限非空的属性集合,V是属性值集合,Va表示属性 a∈A的属性值范围,fa:U→Va是一个信息函数,它指定U中每一个样本 x的属性值。对于每个属性子集 P⊆A定义一个不可分辨关系:

x,y在S中关于属性集P是等价的,当且仅当 fa（x ） = fa（y）对所有的f∈P成立,即 x,y不能用P 中的属性加以区别。在信息系统S={U,A}中,设XU是个体全域上的子集,PA,则X的下近似集:根据现有的数据R,判断U中所有属于或者可能属于集合X的对象组成的集合为:

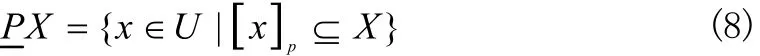
其中[x]p表示等价关系P下包含x的等价类。上近似集:根据现有的数据R,判断U中一定属于或者可能属于集合X的对象组成的集合。即:

其边界区域为:BndP(X ) = PX - PX (10)

P,Q⊆A,如果 IND(P ) ⊆ I ND(Q),则说明集合P依赖于Q,记为P⇒Q,一般采用依赖度来评价两个集合的依赖性,即,

当k=1时,Q完全依赖于P, 0＜k＜1,Q部分依赖于P, k=0,Q完全独立于P。

4 适应度函数

特征选择的目标是在利用最少的特征条件获得最好的分类模型,相比于过滤模式,封装的适应度函数往往能取得更好的分类效果。本文采用封装模式粗糙集的适应度函数:

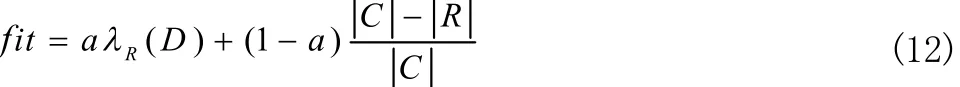
其中 λR( D)表示数据集D相对于条件属性R的分类质量,R表示选择的特征数目,C表示所有的特征数目。其中a、b是调整因子,调整分类质量与被选择特征数目之间对于适应度函数的影响。一般a∈ [ 0,1], b = 1 - a ,前期实验表明,分类质量对于适应度函数的影响明显高于特征数目,因此将a的值设定为0.9,确保分类质量起主导作用。

5 实验设计

为了验证骨干粒子群算法与粗糙集结合的优越性。本文选择离散粒子群算法(BPSO)和遗传算法(GA),同时作用在粗糙集适应度函数上,采用数据集UCI机器学习库中的数据(如表1所示)。设定粒子群种群数目20,迭代次数为100,遗传算法的交叉概率为0.6,变异概率为0.4。比较不同算法作用在相同数据集上的分类效果,同时比较被选特征子集中的特征数目。

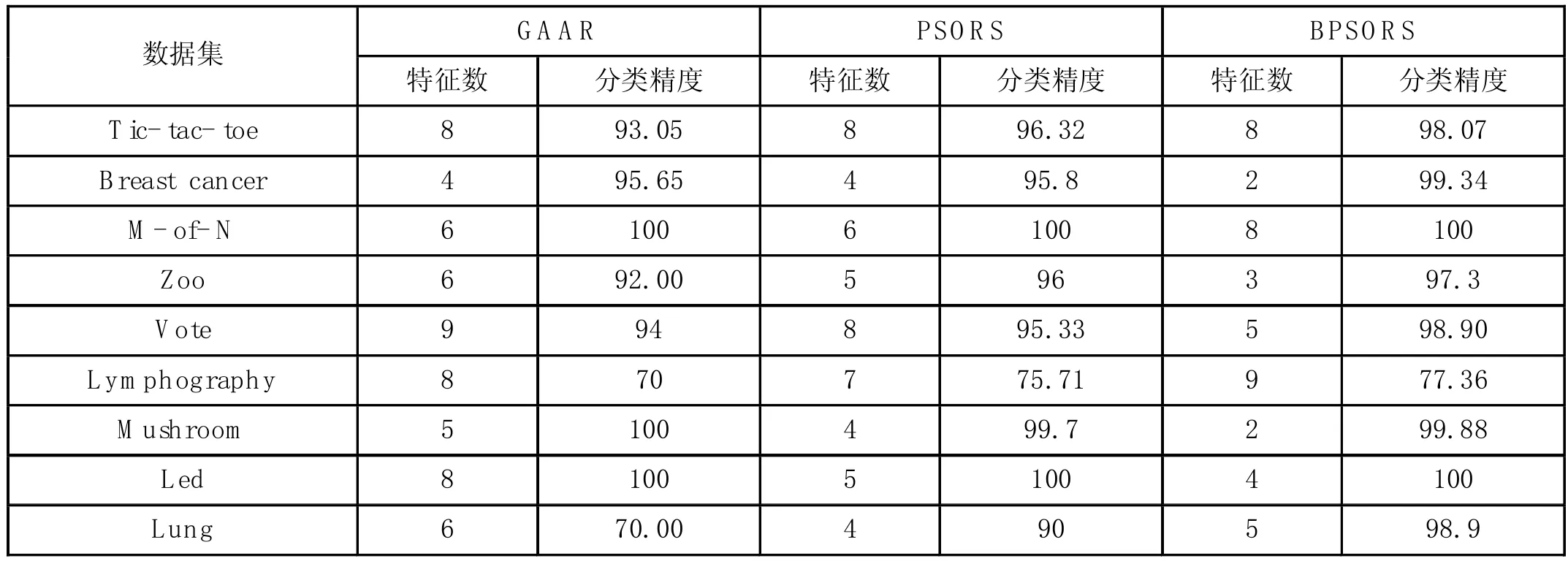
表2 各算法分类效果对比

6 实验结果分析

实验结果如表2所示,三种不同的算法作用于九组不同数据集,比较分类效果以及被选特征数目。总体而言,相比于遗传算法,传统粒子群算法,骨干粒子群在数据分类、约简特征数目上的效果更佳。当在数据集特征数目较少时,例如在数据集Tic-tac-toe 和Breast caner中,骨干粒子群算法相比于其他两种算法在分类的效果上有了一定的提高,特别是对于数据集Breast caner减少了被选特征的数目。随着特征数目的增加,数据集也更加复杂,相比于其他两种算法,基于骨干粒子群的特征选择方法能够取得较好的分类效果。在数据集Vote和Lymphography中,新算法的分类效果明显提高。特别是在数据集Lung中,分类准确率相比于传统粒子群算法提高了近9%。其中数据集Led在迭代的前期就达到了100%的分类准确率,说明骨干粒子群算法具有较快的收敛能力。此外,被选特征数目与分类的准确率随着迭代次数的增加基本上呈现反比例关系,即利用最少的特征数目可以获得最优的模型,当分类的准确率达到最高时,被选特征数目几乎不再变化,该约集简中的特征能够使得这个子集具有与特征全集相同或者更好的分类能力。

7 结语

本文提出一种基于骨干粒子群算法和粗糙集的特征选择方法。将骨干粒子群算法作为特征选择产生过程的搜索算法,将粗糙集作为评价函数。在粒子群算法初始过程中引入混沌模型增加其初始粒子的多样性,同时在更新机制中引入骨干因子增加其全局搜索能力。通过在九组不同特征数目的数据集上进行测试,并与其它优化算法的进行比较,结果表明新的特征选择方法在分类中能够取得更好的效果。

[1]张丽新,王家钦,赵雁南,等.机器学习中的特征选择[J].计算机科学,2004,(11):180-184.

[2]周城,葛斌,唐九阳,等.基于相关性和冗余度的联合特征选择方法[J].计算机科学,2012,(4):181-184.

[3]李志豪.基于离散粒子群算法的粗糙集属性约简[J].工业控制计算机,2016,(11):102-106.

[4]J. Kennedy, R. C. Eberhart. Particle swarm optimization[J].IEEE International Conference on Neural Networks,1995,(4):1942-1948.

[5]J Kennedy. Bare bones particle swarms[J].Swarm Intelligence Symposium,2003:80-87.

[6]J Kennedy , RC Eberhart. A discrete binary version of particle swarm algorithm[J].Systems, Man, and Cybernetics,1997,(5):4104-4108.