基于张量分解的分布式主题分类模型①

马年圣,卞艺杰,唐明伟

1(河海大学 商学院,南京 211100)

2(南京审计大学 管理科学与工程学院,南京 211815)

大数据时代,网络信息纷繁复杂,需要我们从众多网络数据中提取出高价值的隐含信息,挖掘出的分类信息可用于内容推荐、针对性营销以及实时预测等功能.而其中主题分类又是现今网络信息时代的一大研究热点,传统的主题分类主要是以基本分类方法以及人工标签来实现,但是人工干预过多势必影响到最终的分类结果,这就需要我们寻求一个无监督的方法,从文档信息的采集到最后的结果输出无需人工参与.

LDA (Latent Distributed Allocation)主题模型便是一个无监督的数据挖掘方法,该模型可从大规模数据中进行文档主题的抽取,能够出色地完成挖掘文本的潜在关系、判别关联性等工作,显著提高信息的分类及利用效率.LDA模型参数计算的空间以及时间复杂度较高,并且对软硬件需求也提出高要求,所以模型参数求解优化一直是研究热点.Blei等人采用“变分推断-EM”算法进行LDA模型参数计算,在单机模式下,随机变分推断快速而准确,但是在分布式计算中因交互过高而显疲态[1];批量变分推断具有很高的交互效率,但在计算E-step时并行效率差强人意[2];马尔可夫链在分布式同步和异步计算方面体现出较好的移植性,但其计算效率过低还有待优化[3];唐晓波等人采用热度进行模型参数计算的优化,通过求解微博的热度来实现信息的分类工作,其结果也更加直观,但是其热度的计算方法比较单一,并不适用于其他的网络数据的分类工作[4].

而在LDA模型的针对性使用方案方面也进行了大量研究,Ramage等人提出Labeled LDA模型进行有监督的主题分类,在主题建模中添加文档的标签,克服了原始模型强制分配主题的缺陷,但是也使得计算量翻倍增加[5];桂思思等人融入多时间节点函数进行用户兴趣的预测,但是时间差值的确定比较主观,偏差不可避免[6];关鹏等人采用生命周期理论同主题模型结合,能够展现所观察文本的随时间所发生的变化,然而参数的计算没有改进为适合生命周期理论的方法[7].

上述国内外对于LDA主题模型的改进都针对特定的数据分类,而在处理数据量大、维度较高的网络信息时效率、准确性等问题便凸显出来,且上述研究大部分都是单机下进行实验,平台移植性较差.LDA主题模型涵盖了大量的数据以及变量,构成了高维数据问题,在时间轴上产生了大量的多元数据,其中也包含很多数据噪声,而张量分解方法能够通过数据降维以及张量近似的方法来优化计算.本文通过随机奇异值分解和白化变换将主题模型参数计算转化为三阶张量的CP分解,加之以ALS算法以及数据处理技术,极大地提高了并行化和准确性,可达到更高的收敛率以及抗干扰性.本文实验在Spark集群上进行,充分发挥Spark作为轻量级大数据处理框架的特点,及其大规模数据的计算效率明显优于Hadoop的特性.改进后的LDA计算模型适用于大数据时代复杂且高维的信息特点,能够出色地完成巨量网络信息的分类工作,适用于搜索引擎、文本解读、信息推送等数据应用领域.

1 相关基础理论

在国内外学者的讨论当中,LDA主题模型暴露出其不足的方面,单机模式下,模型训练时间长,精确度不高,并且对于模型超参求解的要求较高,这些都对模型的发展应用提出了挑战.现被广泛使用的LDA参数求解方法有变分推断和马尔可夫链,但数据量较大的情况下,两种方法的计算效率还是比较低下,这就需要我们采用“分治”思想,选用张量分解的方法来优化模型参数计算,采用更高效率和精确度的降维计算方法,同时使用分布式计算模式来提升模型训练的效率,以适用于网络大数据量文本的主题分类推荐.

1.1 LDA主题模型

潜在狄利克雷分布模型LDA由Blei等人于2003年提出后,便被广泛应用于观点挖掘、主题相关性和信息检索等领域[8].LDA通过对离散数据集的建模,从中提取文本隐含主题,能在海量网络数据中自动寻找信息间的语义主题,克服传统信息检索中文档相似度计算方法的缺陷.LDA主题模型属于词袋模型,它认为文本中包含着无序的词语,参数空间的规模与训练文档数量无关,适合处理大规模语料库.同时作为全概率生成模型,LDA主题模型的突出优点是具有清晰的层次结构[9],LDA是一个三层的贝叶斯框架模型,每一层都有相应的随机变量或者参数控制,包含词汇、主题、文档的三层结构,数据集中的文档被看作是有限个隐含主题所构成的混合分布,而相应的每个主题也都是对应的数据集中一组特征词汇的混合分布,模型的概率图如图1所示.

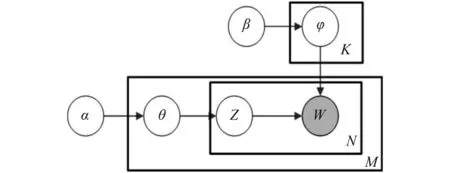
图1 LDA主题模型概率图

图1中,只有W是可观察到的变量,其他都是隐含变量或者参数.其中,φ表示“主题-词语”分布,θ表示“文档-主题”分布,α、 β分别是 θ和 φ的先验分布,N表示文档的单词总数,M表示文档的总数,Z为选定的主题,由以上LDA主题模型概率图可得到主题生成的联合概率如公式(1)所示：

LDA模型训练便是求得参数 α和 β的值,使P(θ|α,β)为最大.同LSA和PLSA模型会产生的过拟合问题不同,LDA主题模型采用狄利克雷分布,从而简化了模型的推导过程,并且具有很好的先验概率假设,参数数量不会随着文本数量的增长而线性增长,泛化能力强,在算法复杂度和展示效果方面表现优越,广泛应用于文本的处理当中.

1.2 CP分解

CP分解,即Candecomp/Parafac分解,是传统矩阵分解的拓展,广泛应用于信号传输、数据分析等领域,它是把张量分解为一系列rank-one张量的计算过程,对于一个三阶张量分解可以写成如下的向量和的形式：

其中,⊗表示张量积运算,R表示张量的秩公式(2)中三阶张量也可写成如下元素乘和的等价形式：

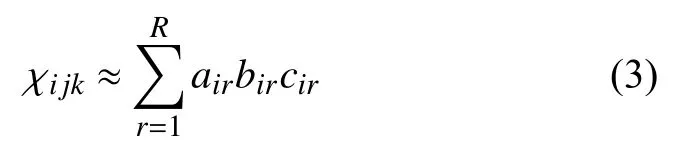
式中根据公式(3),CP分解便将张量表示为有限数目的rankone张量之和,分解模型如图2所示.

图2 CP分解模型

CP分解具有唯一性,其实质上指的是张量的秩分解是唯一的,而传统的矩阵分解并不是唯一的[10].目前已有多种方法可以计算CP分解,其中最简单有效的是交替最小二乘法(Alternating Least Square,ALS),也是本文所选用的张量分解方法.对于三阶张量ALS的思想是找到R个rank-one张量或者一组因子矩阵来逼近如公式(4)所示：

式中,符号⊙表示Khatri-Rao积,当满足一定的迭代条件时,迭代终止.因为ALS算法需多次迭代才收敛,所以我们将算法应用到Spark平台中进行分布式计算,以求快速的求得全局的最优参数,减少大量的实验时间,这也是分布式计算在现今模型求解中的优势之处.

2 基于张量分解的主题分类模型

2.1 基于张量分解的LDA主题分类主体模型

在LDA主题模型中,每篇文档都存在着K个潜在的主题,第k个主题具有“主题-词语”的条件分布概率将所有主题的条件分布概率组成矩阵为总词汇量,则 φ便是模型求解的“主题-词语”分布矩阵.而在第m篇文档中,其混合分布的潜在话题是根据狄利克雷先验参数所求得,已知先验参数分布下,便可求得文档m的“文档-主题”分布矩阵

传统的LDA主题模型的参数估计方法包括变分推断,马尔可夫链等,本文采用矩量法将参数估计转化为张量分解的方式进行迭代.主题为的LDA主题模型可通过文本词汇表示为张量的形式,Anandkumar等人[12]对主题模型张量的表现形式有如下定义.

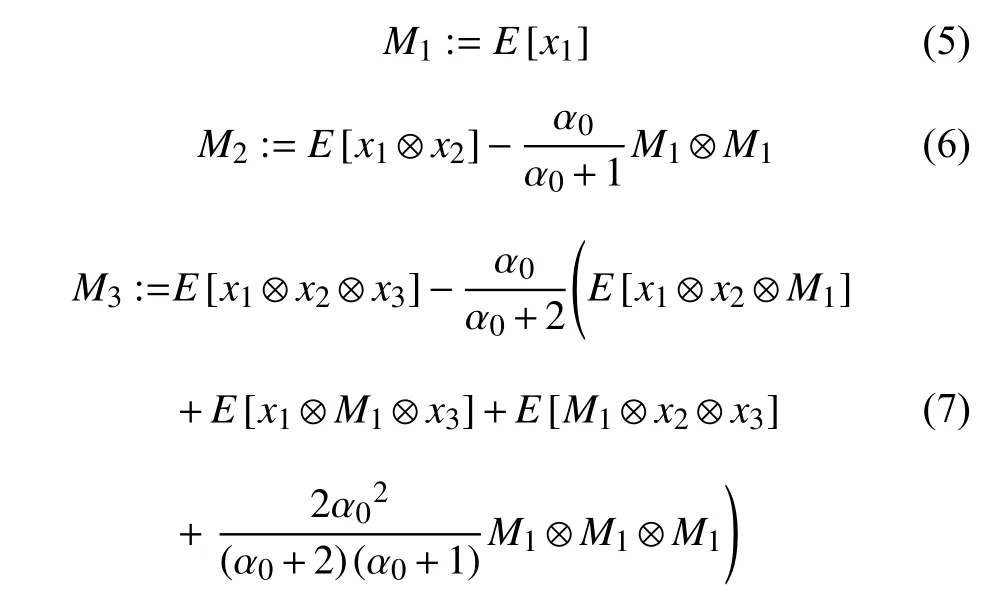
其中表示一个词语,V为文档集中所有的词汇,为同一篇文章的词语,对于词语v,任意u≠v,符号 ⊗为张量积运算,任意的E为向量期望表示话题分布的稀疏程度,α0越小,表明文档中隐含的主题越少.张量M2、M3通过分解可转化为如下张量积的表现形式：

其中,K为我们从文档集中抽取的主题数,通过公式(5)～(9),主题模型参数求解便可转化为矩阵张量分解的方式.从公式(8)可以得出二阶矩M2的低秩分解可求得包含 αk和 φk的子空间,而M3的张量分解可求得潜在狄利克雷先验分布 α以及“主题-词语”分布矩阵,最终通过先验分布 α求解“文档-主题”矩阵.

在进行M3张量分解分解前,通过数据的预处理(包括数据向量化、正交化和降维操作等)来保证模型的收敛率和抗噪声干扰,随机奇异值分解[13]作为高效的矩阵低秩分解手段,此处选用该方法来执行对的正交分解,接下来利用矩量法将LDA主题模型参数估计转化为低维下张量的CP分解,最终生成“文档-主题”、“主题-词语”矩阵.模型参数求解步骤如表(1)所示.

模型最终会生成“文档-主题”、“主题-词语”概率分布,根据“文档-主题”矩阵可选取概率最大的主题为该文档的第一候选主题,而通过“主题-词语”矩阵可推断是该主题的具体含义,结合文档中已经得出的候选主题,便可实现该文档的主题分类.

表1 基于张量分解的主题分类模型求解步骤

2.2 模型的关键技术

2.1小节中基于张量分解的LDA主题分类模型可拆分为3个重要阶段,第1阶段为数据预处理,第2阶段为基于ALS算法的CP分解,第3阶段为主题分类计算.

(1) 数据预处理

网络信息不同于普通文本信息,数据形式、结构均有差异,所以预处理的首要工作便是进行分词等一系列操作,数据预处理完成后,需对数据进行向量化以及降维操作,以便大量减少参数迭代时的计算量.在进行张量形式的多维数组操作时,数据维数的大小直接决定了矩阵操作的计算量大小,尤其是在处理自然语言这种高维数据时,在内存中进行三阶矩的存储操作的运算量都是极大的.数据稀疏化是其中一类方法,更好的则是进行线性降维,加之以张量乘积的形式来避免直接生成张量,能够大幅度减少计算规模,并且对于张量的操作也是高效的[14].

在此首先进行张量白化变换(Whitening Transformation),低秩正交分解二阶矩.奇异值分解在进行矩阵分解中表现出极大的优势,但当数据的行列数过大时,奇异值分解表现出分解缓慢、效率低等缺点,而随机奇异值分解通过生成子空间进行迭代运算能够加快分解工作,此处采用随机奇异值分解进行的分解操作[13].

随机奇异值分解算法可以总结为两步计算,第一阶段构造一个正交基,其值域接近于M2,即构造正交矩阵Q,使得第二阶段将矩阵约束于K维子空间中,运用奇异值分解来计算QTM2,求得U、Σ、Z.

由随机奇异值分解可得定义为白化矩阵,令则便是正交向量,证明如下：

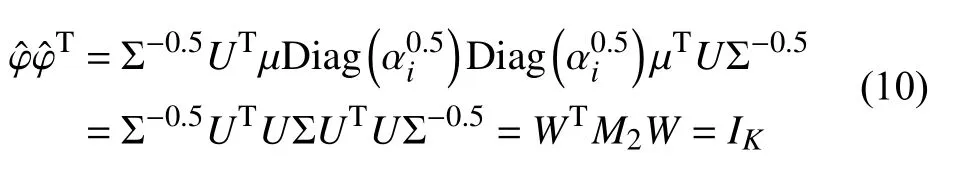
最后使用公式(7)可计算生成维数为K3的正交三阶矩至此,便完成了M3白化以及正交化操作,即数据预处理阶段结束.

(2) 基于ALS算法的张量分解

计算生成后,运行基于交替最小二乘法的张量分解,ALS算法的核心是找到最接近的有限数目的rank-one之和[11],即为：

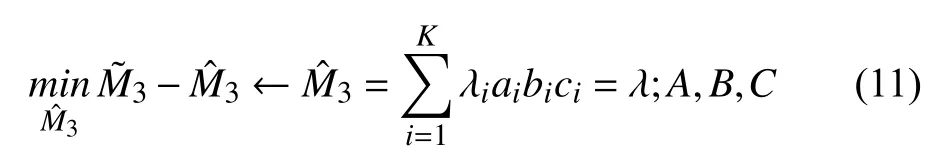
其中,为分解的rank-one之和,交替最小二乘法是一个迭代算法,算法交替的进行A,B,C的优化,每一次迭代过程中,总是假定其他两个矩阵是已知的,通过求解最小化的问题来分解矩阵.当B和C值固定后,可以将公式改写为如下形式：

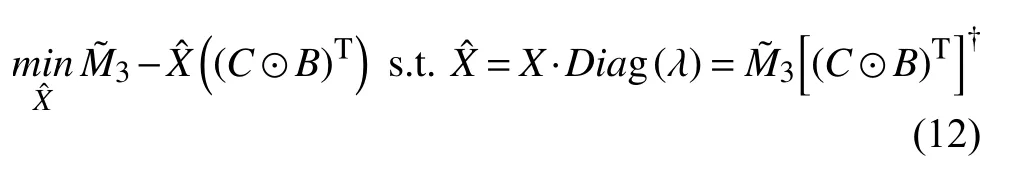
将ˆ 带入最小值求解中,最终基于交替最小二乘法的张量分解便转化为如下的最优化计算：

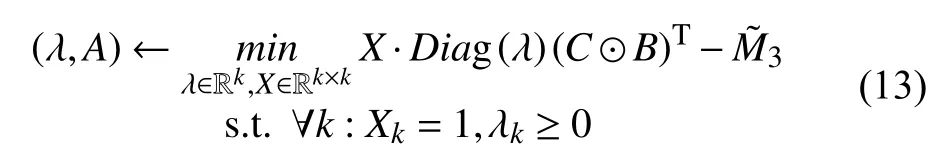
其中,⊙表示Khatri-Rao积,每次迭代都进行 λ的计算以保证特征向量每一列均为归一化,此处采用Khatri-Rao积的伪逆矩阵形式优化计算[15],如公式(13)所示：

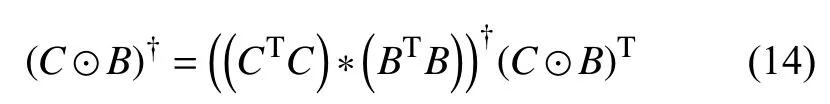
式中,∗为哈达马乘积,通过变换,仅需计算K×K的伪逆矩阵而无需计算K×K2原矩阵.ALS算法是一种批量同步并行计算模型[16],在K阶并行的保证下,公式(11)中左边的每一行均可作为独立的一部分来进行参数的估计,并且在使用Spark计算框架进行分析时,每运行一个ALS子程序之前可通过广播变量同步最新估计的参数[17],进行算法迭代时的空间需求以及每个节点所进行的总交互量均为

(3) 模型主题分类计算

张量分解收敛后,采用反白化变换,计算原文档集中的狄利克雷先验分布以及“主题-词语”分布矩阵.反白化变换强调张量结构的特殊性[12],通过分解后的张量数据来投影反射出LDA模型参数,如下所示：

给定CP分解后的向量线性无关,标量均大于0,则：

①的特征值和特征向量分别为

②原词汇空间的狄利克雷先验参数

③是的穆尔彭罗斯伪逆矩阵[18],原词汇空间的“主题-词语”分布概率

由反白化变化可推导出同时给定分解后的特征向量,求解矩阵使得待原词汇空间参数求解后,根据原输入文档集和先验分布生成“文档-主题”分布矩阵最后,为了更直观的显示以及更精准的分类,将“文档-主题”、“主题-词语”矩阵进行概率排序,在进行文档分类时需指定特定的分类类别,所以我们根据文档中的重点主题以及主题中的重点词语,选取其中概率最高主题为该文档的主题类别,抽取概率为前20的词语作为该主题的特征词,进行下一步的主题分类工作.

3 仿真实验

3.1 平台构建

实验包括模型对比和主题分布分析,实验数据通过WebMagic爬虫技术在网络上自动抓取,通过对页面的分析来下载相应的新闻信息文本,主要采集于各大新闻网站的新闻信息数据,如“中国新闻网”、“凤凰网”等,主要涉及经济、军事、文化等领域,在进行文本的白噪声处理后,筛选出1800条作为原始分析数据.为保证实验的可靠性以及可识别性,需定义停用词表,词表中包含常用词、常见语气词、助词等高频率出现的词语,同时根据中文文本的特殊性,还进行了繁简转换,保证实验数据的格式统一,通过该停用词典可剔除大部分的噪声词语[19].

实验使用Scala作为编程语言,在Spark集群模式上进行模型训练与预测,主节点master进行任务调度,从节点worker进行同步的运算.worker之间交替的计算更新的参数,广播参数至其他的节点,最后进行数据的同步.而master则负责检查是否实时的检验是否需要结束运算以及负责各节点资源之间的调度,实验集群均为Centos 7系统,每个节点内存均为4 G,实验主要步骤如图3所示.

图3 仿真实验步骤

3.2 实验结果与分析

实验首先将模型训练时间和困惑度同基于EM算法的LDA模型进行对比,其中,模型生成时间是体现模型计算是否高效的重要指标之一,而困惑度则是衡量模型是否同原始数据相吻合的重要检验标准,最后通过网络新闻数据的预测,来说明基于张量分解的LDA主题模型适用于网络数据的分类工作.

(1) 训练时间对比

在相同运行环境下,设置迭代次数为500次,主题数为50,将本文模型同基于EM算法的主题模型进行训练对比,通过增加计算节点数来对比模型训练时间长短,结果显示基于张量分解的主题模型在时间方面显现出极大的优势,如图4所示.

图4 模型时间对比图

从图中可以看出,基于张量分解的主题模型在训练时间明显优于基于EM算法的LDA主题模型.增加节点数对于运算时间的减少是明显的,体现出Spark大数据平台在各节点内存不变的情况下,节点个数对于运行时间是成反比的.两个算法开始增加节点数对于时间的优化更是相当显著,但随着节点数的增加,增益效果降低,同基于EM算法的LDA主题模型相比,基于张量分解的LDA模型在节点数增加时,其计算时间下降幅度更大,表明基于张量分解的LDA主题模型对多节点的集群有更好的计算能力,更加表现出模型对于大运算量的适应性.

(2) 困惑度对比

困惑度作为文本建模中常用的评价指标,其值越小,模型对于上下文的约束能力就越强,表明语言模型吻合度越好[8].其公式如下所示：

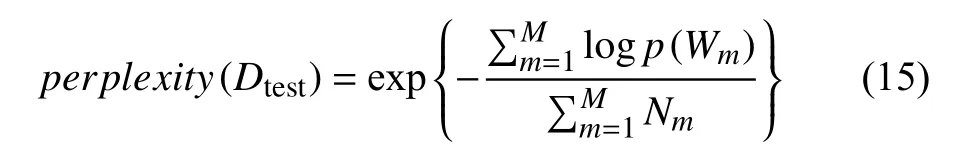
式中,Dtest为测试文档集,Wm为测试m文档中观测到的单词,P(Wm)为模型产生文本Wm的概率,Nm为文档m的单词数.

在相同的语料和参数设置下,计算基于EM算法的LDA主题模型和基于张量分解的主题模型,两种方法困惑度随隐含主题数目的变化情况如图5所示.

通过图5可得到,随着主题数量的不断增加,两个模型的困惑度都在相应的降低,在达到最低点时,主题抽取的个数各不相同,基于张量分解的LDA主题模型在该训练文档集中主题数为50时困惑度最小.在数据量较大、主题较多时,本文模型困惑度明显低于基于EM算法的LDA主题模型.

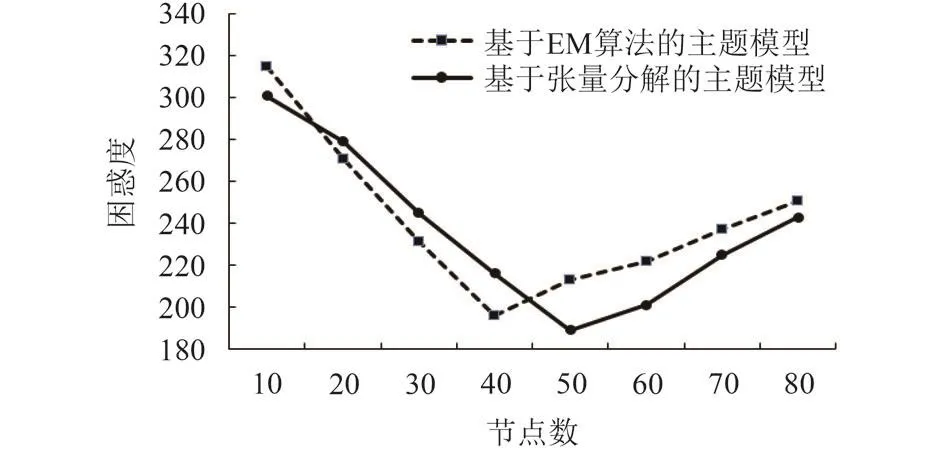
图5 抽取主题数的困惑度对比

(3) 主题分布分析

将预处理的新闻信息通过本文LDA主题分类模型进行训练,针对新闻文本的特殊性,在定义特征词时,进行数据预处理时加入了时间等词的停用,设置主题数为待模型预测完成后,随机抽取三个文档以及他们相对应的主题进行分析,部分结果如表2、表3所示.

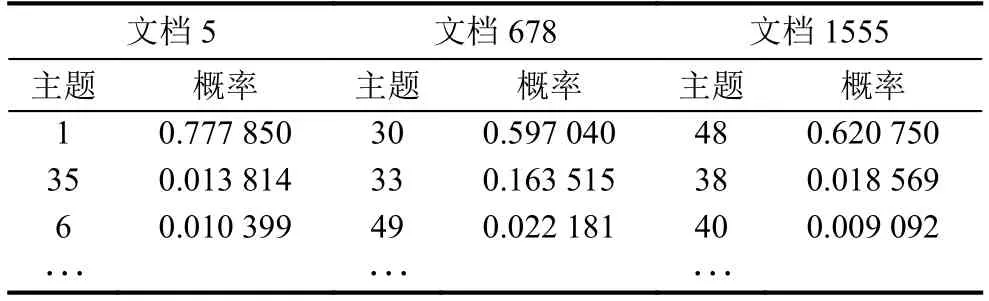
表2 topicN= 50时文档与主题的分布概率

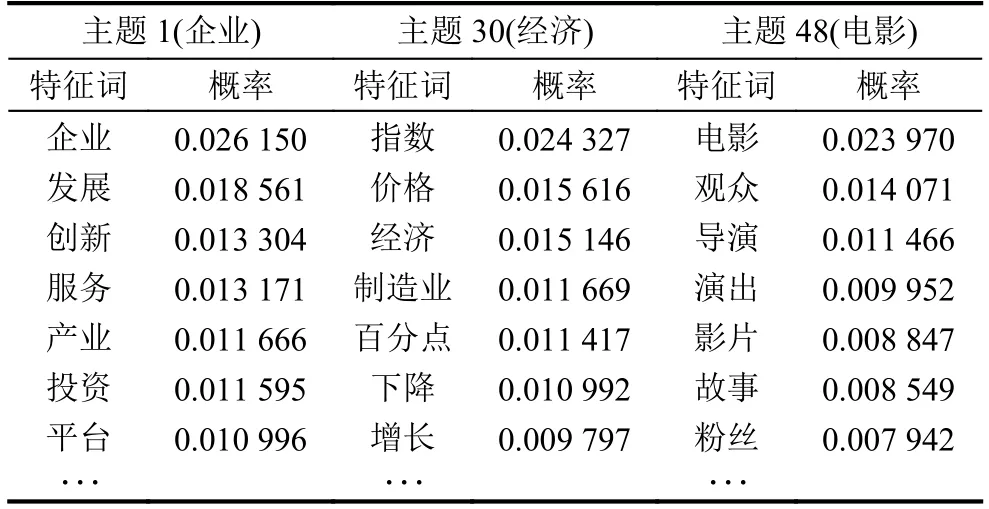
表3 topicN= 50时主题与词的分布概率

表2可以看出,每篇文档根据文中词语的分布,不局限于单个主题,但第一个主题的概率较大,可以整体概括整篇文档的大概主题方向.例如文档5中主题1的概率为0.777 85,相对应,主题一中出现的都是企业发展类的词汇,则主题1便为企业主题,进一步的将文档5便可分类到企业模块.

表3清晰地展现出不同主题其中的含义,可读性强,同时本文实证数据来源于网络新闻信息,从中可窥探社会热点.主题1涉及企业发展,其大部分的词语均是企业在现代社会发展所重视的方面,同时也是企业发展中强调的高频词.而主题30则是经济类,通过各经济词语的罗列,能够对部分的金融的专业用词有一定的了解,可运用于新闻定位推送,同时在新闻里出现,更能说明媒体以及公众对于经济的关注.最后主题48则为文化产业电影类,新闻中能够涉及到如下的词语,说明人们在现今生活高压力下对于电影、文化的关注.以上的“主题-词语”分布能够说明主题模型对于网络数据分类的高效性,显性地挖掘网络信息中所蕴含的内涵,可充分适用于信息推荐、搜索引擎当中.

4 结论与展望

本文将张量分解引入到LDA主题模型的训练中,利用矩量法将数据转换为张量分解的计算形式,运行基于交替最小二乘法的CP分解进行参数迭代,最后使用网络数据在大数据平台Spark中验证分析,实验表明,基于张量分解的LDA主题模型在网络数据主题、词汇生成方面同基础主题模型更有优势,更加适用于网络数据主题的分类.当然,网络数据的预处理准确性有待提高,对于主题模型的原始输入以及计算优化是我们下一阶段需要研究的内容.

1 Hoffman MD,Blei DM,Wang C,et al.Stochastic variational inference.Journal of Machine Learning Research,2013,14(5)：1303-1347.

2 Nallapati R,Cohen W,Lafferty J.Parallelized variational em for latent dirichlet allocation：An experimental evaluation of speed and scalability.Proceedings of 2007 Seventh IEEE International Conference on Data Mining Workshops(ICDMW 2007).Omaha,NE,USA.2007.349-354.

3 Griffiths TL,Steyvers M.Finding scientific topics.Proceedings of the National Academy of Sciences of the United States of America,2004,101(S1)：5228-5235.

4 唐晓波,向坤.基于LDA模型和微博热度的热点挖掘.图书 情 报 工 作 ,2014,58(5)：58-63.[doi：10.11925/infotech.1003-3513.2014.05.08]

5 Ramage D,Hall D,Nallapati R,et al.Labeled LDA：A supervised topic model for credit attribution in multi-labeled corpora.Proceedings of 2009 Conference on Empirical Methods in Natural Language Processing.Singapore.2009.248-256.

6 桂思思,陆伟,黄诗豪,等.融合主题模型及多时间节点函数的用户兴趣预测研究.现代图书情报技术,2015,(9)：9-16.[doi：10.11925/infotech.1003-3513.2015.09.02]

7 关鹏,王曰芬.基于LDA主题模型和生命周期理论的科学文献主题挖掘.情报学报,2015,34(3)：286-299.

8 Blei DM,Ng AY,Jordan MI.Latent dirichlet allocation.Journal of Machine Learning Research,2003,3(4/5)：993-1022.

9 李湘东,胡逸泉,黄莉.采用LDA主题模型的多种类型文献混合自动分类研究.图书馆论坛,2015,35(1)：74-80.

10 Sidiropoulos ND,Bro R.On the uniqueness of multilinear decomposition of N-way arrays.Journal of Chemometrics,2000,14：229-239.[doi：10.1002/(ISSN)1099-128X]

11 Kolda TG,Bader BW.Tensor decompositions and applications.SIAM Review,2009,51(3)：455-500.[doi：10.1137/07070111X]

12 Anandkumar A,Foster DP,Hsu D,et al.A spectral algorithm for latent dirichlet allocation.Algorithmica,2015,72(1)：193-214.[doi：10.1007/s00453-014-9909-1]

13 Halko N,Martinsson PG,Tropp JA.Finding structure with randomness：Probabilistic algorithms for constructing approximate matrix decompositions.SIAM Review,2010,53(2)：217-288.

14 Anandkumar A,Ge R,Hsu D,et al.Tensor decompositions for learning latent variable models.The Journal of Machine Learning Research,2014,15(1)：2773-2832.

15 Liu SZ,Trenkler G.Hadamard,khatri-rao,kronecker and other matrix products.International Journal of Information and Systems Sciences,2008,4(1)：160-177.

16 Valiant LG.A bridging model for parallel computation.Communications of the ACM,1990,33(8)：103-111.[doi：10.1145/79173.79181]

17 Wang YN,Tung HY,Smola A J,et al.Fast and guaranteed tensor decomposition via sketching.Proceedings of 2015 Advances in Neural Information Processing Systems (NIPS).Montreal,Canada.2015.991-999.

18 Macausland R.The moore-penrose inverse and least squares[Thesis].Tacoma,Washington,USA：University of Puget Sound,2014.

19 冯永,李华,钟将,等.基于自适应中文分词和近似SVM的文本分类算法.计算机科学,2010,37(1)：251-254,293.