镁质红土镍矿酸浸结果影响因素的数学模型
2018-06-13王宇斌彭祥玉张小波雷大士
王宇斌, 文 堪, 彭祥玉, 张小波, 雷大士
(西安建筑科技大学材料与矿资学院, 陕西 西安 710055)
近年来选厂自动化和精确化水平逐渐提高,极大地推动了选矿数学模型的应用[1-3]。选矿数学模型能够定量分析各种影响因素对选别指标的影响程度,并且可建立选别指标与这些影响因素间的函数表达式[4-5],因而在选矿设备试验研究中应用广泛[6-11],但在选矿试验研究中应用较少。红土镍矿酸浸过程中,影响镍浸出率的因素较多,为揭示不同因素对镍浸出率的影响规律,进而确立各变量之间存在的相关关系,最终建立变量间合适的回归方程及数学模型,并为优化现场生产条件提供依据。本研究以某低品位镁质红土镍矿为原料,采用正交试验的方法进行常压酸浸试验,对试验结果进行正交多项式回归分析,建立了各因素与镍浸出率之间的数学模型。研究可为类似选矿试验建立数学模型提供参考,并为实际生产提供理论支撑。
1 试验
1.1 试验原料
为明确原矿中所含元素的种类、含量以及镍的物相,对试样分别进行了化学多元素和原矿镍物相分析,结果如表1和表2所示。

表1 试样多元素分析结果 %
由表1和表2可知,原矿中主要含有Ni、MgO、Fe等,其中镍的含量较低,仅为0.62%,且镍主要以硅酸镍的形式存在;铁的含量为14.95%,氧化镁含量较高为28.58%,由于原矿中含MgO较高,因此酸耗较大。结合岩矿鉴定分析结果可知,原矿中镍的崁布粒度较细且所含矿物种类较为复杂,主要包括镍蛇纹石、镁橄榄石、磁铁矿和铬铁矿等矿物,可见浸出因素对镍的浸出率影响较大。
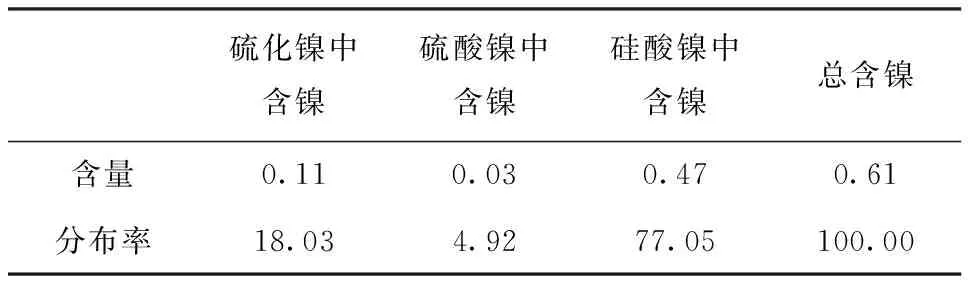
表2 试样镍物相分析结果 %
1.2 试验方法
原矿先进行破碎- 磨矿预处理,然后称取经筛分至-0.074 mm的试样300 g,将试样置于烧杯中,加入一定量的硫酸配成所需浓度的矿浆,在一定温度下进行浸出并计时,浸出结束后过滤,对浸渣多次洗涤,化验浸渣的镍品位并计算镍的浸出率。
2 正交试验设计
本研究参考前期探索试验结果并结合理论分析,主要考察硫酸浓度、液固比、浸出时间、搅拌速率及浸出温度等因素,采用五因素四水平的正交方法进行试验,选取各因素的水平用量在适当的范围内,进行两次酸浸试验,取两次试验的镍浸出率平均值作为最终结果,各因素水平及用量见表3,正交试验设计方案及结果见表4。

表3 正交试验各因素水平表

表4 酸浸正交试验设计方案及结果
注:EⅠ、EⅡ、EⅢ和EⅣ分别为每列中该因子相同水平所对应的数据之和;ET为全部数据之和;CT为校正项;S为变差平方和。
由表4可知,试验16获得的镍浸出率最高,平均值可达95.57%,试验1所得的镍浸出率最低,平均值仅为35.54%。由表4还可看出,试验 2、5、9和10获得的镍浸出率相对较低,均在60%~80%之间,而试验3、4、6、7、8、11、12、13、14和15所得的镍浸出率相对较高,均在80%~100%之间。
3 正交试验结果的回归分析
在已知各因素之间没有交互作用的情况下,为得到镍的浸出率与各因子之间的定量关系,对镍浸出率进行回归分析。多项式的回归问题可以转换成多元线性回归来计算[12-13]。当因素水平的间距相等时,可以利用正交多项式回归处理正交试验结果,进而得到镍浸出率与各因素之间的定量关系。当试验水平为4时,表明函数关系为三次多项式,查询正交多项式表[14],设三次多项式的回归方程为:
(1)
式中:y为响应值,b为回归系数,φ1(x)、φ2(x)、φ3(x)分别为x的一次、二次和三次多项式。
该正交多项式的系数如表5所示,计算式如下:

表5 正交多项式的系数
φj(x′)=λjφj(x′)
(2)
φ0(x′)=1
(3)
(4)
(5)
(6)
式中:N为观测值的次数,λ为调整系数。
由上式得到正交多项式计算值公式:
(7)
(8)
(9)

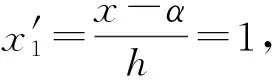
(10)
将上式代入三次多项式的回归方程后得:
(11)
为建立最优的回归方程,先判断各因素效应的显著性,因此先对各因素的一次项、二次项和三次项的方差比较分析,决定各项次的取舍。根据表5中正交多项式的系数列成表6,其中φ1(A)、φ2(A)、φ3(A)表示因子A的一次项、二次项和三次项;φ1(B)、φ2(B)、φ3(B)表示因子B的一次项、二次项和三次项;φ1(C)、φ2(C)、φ3(C)表示因子C的一次项、二次项和三次项;φ1(D)、φ2(D)、φ2(D)表示因子D的一次项、二次项和三次项;φ1(E)、φ2(E)、φ3(E)表示因子E的一次项、二次项和三次项,计算结果如表6所示,其中:
Bi=Σ(c×η)
(12)
Di=s×n×r
(13)
di=Bi/Di
(14)
(15)
式(12)和(13)中的多项式系数c及平方和s由表5可知;η为两次浸出率之和;n为试验重复次数,且n=2;r为重复使用S的次数。根据表6可得各个因子平方和Q,作进一步的方差分析,结果见表7。
由表7的方差分析结果可知,硫酸浓度、液固比和浸出温度是影响镍浸出率的显著因素,而浸出时间及搅拌速率是影响镍浸出率的次要因素,并且由表7也可得知各个因素的效应项显著性,其中因子A1、B1、E1的影响特别显著,因子E2的影响显著,其余因子影响均不显著。因此根据式(11)列出有影响的因子A1、B1、E1、E2的回归方程式如下:
(16)
根据式(10)可求得因子A试剂浓度的水平差为h=0.3
则α=A-0.3=4.3-0.3=4
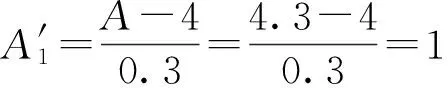

表6 方差的各项结果
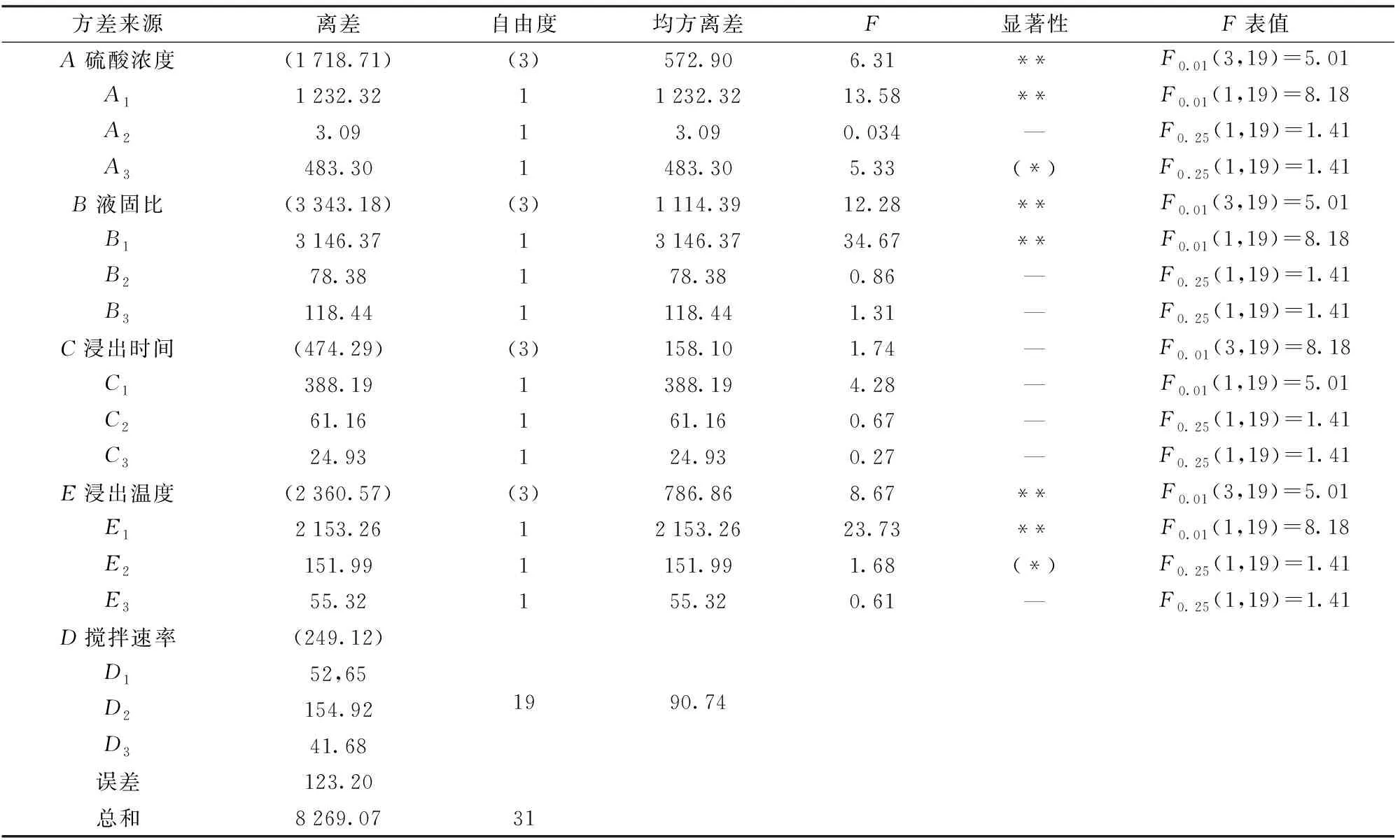
表7 镍浸出率方差分析

(17)
同理可得:因子B液固比的水平差为h=0.5,
则α=B-0.5=2.5-0.5=2


(18)
因子E浸出温度的水平差为h=10
则α=B-10=70-10=60


(19)
以此带入式(16)整理可得:
(20)
式(20)就是通过试验求得的表述红土镍矿镍的浸出率与A硫酸浓度、B液固比和E浸出温度之间相关关系的回归方程,也是该红土镍矿浸出反应的数学模型。将各个因子水平代入式(20),即可得到镍浸出率的预测值,且该预测值与两次试验结果平均值之差的平方和即为镍浸出率残差的标准差,计算结果见表8。

表8 镍浸出率的残差估计
(21)
式(21)中m为测试次数,且m=16,S为试验值与预测值的误差(%),由此可估算一定范围内(硫酸浓度4.3~5.2 mol/L,液固比2.5∶1~4∶1,浸出温度70~100 ℃)各种条件下镍浸出率的预测值。
4 结论
(1)该低品位镁质镍矿酸浸试验过程中影响镍浸出率的显著因素为硫酸浓度、液固比和浸出温度,不显著因素为浸出时间和搅拌速率。
(2)在回归分析的基础上建立了红土镍矿酸浸镍浸出率与硫酸浓度、液固比和浸出温度之间相关关系的数学模型,根据该模型可估算并预测在一定范围内不同条件下镍的浸出率。
(3)研究对进一步优化红土镍矿酸浸试验条件和类似选矿试验数学模型的建立具有重要参考意义。
[1] 韩登峰. 基于给矿速率的KYZ- B型浮选柱试验选型数学模型的建立与分析[J]. 有色金属(选矿部分),2015(4):72-74,83.
[2] 田娟,樊民强. 磁铁矿磁性物含量与TFe品位关系的数学模型[J]. 中国矿业,2013(10):105-108.
[3] 贾清梅,李富平,太军君,等. 某钽铌矿品位指标优化中数学模型的建立[J]. 金属矿山,2010(9):84-86,145.
[4] 张国祥. 我国选矿数学模型研究现状及展望[J]. 国外金属矿选矿,1986(9):1-5.
[5] 李松仁. 国外选矿数学模型及计算机应用现状[J]. 国外金属矿选矿,1984(9):1-10.
[6] 时杰. 磁选柱数学模型及计算机模拟[D]. 昆明理工大学,2009.
[7] 王卫星. 螺旋溜槽分选过程的随机数学模型[J]. 有色金属,1994(3):37-41,6.
[8] 刘胜利. 皮带溜槽的选矿数学模型[J]. 有色矿冶,1991(6):14-15.
[9] 汪廷煌. 摇床基本数学模型的研究[J]. 昆明工学院学报,1991(6):10-14.
[10] E.G.Kelly,魏德洲. 螺旋选矿机数学模型的建立与应用[J]. 国外金属矿选矿,1989(10):31-37.
[11] 汪廷煌. 圆锥选矿机的经验数学模型[J]. 云南冶金,1987(5):28-32.
[12] 段涛,彭同江. 蛇纹石酸浸结果影响因素的正交多项式回归分析[J]. 西南科技大学学报(自然科学版),2005(2):42-46.
[13] 王泽红,陈晓龙,袁致涛,等.选矿数学模型[M].北京:冶金工业出版社,2015: 86-89.
[14] 陈炳辰. 选矿数学模型[M].沈阳: 东北工学院出版社,1990: 55-58.
