钟差预报模型的分析和比较

王向磊

(北京卫星导航中心,北京 100094)

0 引 言

时间是卫星导航定位的基础,对位置的精确测量实际上是对时间的精确测量。卫星在空间轨道飞行时,卫星钟与地面时间基准的比对不可能是连续进行的,也就是说,在地面监测站观测不到的弧段内,卫星钟与系统时间之间的同步只能靠卫星钟自己来维持。这就需要根据卫星钟的运行性能,建立准确的卫星钟预报模型。

导航卫星在轨原子钟的预报精度决定了星历更新频度,决定了地面运控系统的复杂性和工作量,其预报精度不仅与频标特性有关,还会受到预报算法复杂性的限制。

文献[1]和[2]中,作者对一、二阶多项式模型的钟差预报精度进行了分析和比较;文献[3]和[4]对一、二阶多项式模型和灰色系统模型的钟差预报精度进行了分析和比较;本文针对GPSBLOCK IIR-M卫星的卫星钟,利用IGS提供的精密钟差数据,对文献[1]和[5]及[6]中的多项式模型、切比雪夫多项式模型以及灰色系统模型的钟差预报精度进行综合分析和比较,最后得出了一些初步结论。

1 多项式模型

卫星钟读数T与系统时间t之间的关系可以用一个多项式来表示[1],有

T-t=a0+a1(t-t0)+a2(t-t0)2+

…+am(t-t0)m,

(1)

式中:a0、a1,…,am是钟差模型的拟合系数;m为多项式阶次,本文中,m=1,2,3.

设相对于时间ti的钟差为xi,观测误差为vi,可以建立误差方程：

xi+vi=a0+a1(ti-t0)+a2(ti-t0)2+

…+am(ti-t0)m,

(2)

(3)

(4)

其中：n为钟差数据个数； Δti=ti-t0.预报残差均方根可按下式计算

(5)

2 切比雪夫多项式模型

设x(t)为采样间隔为τ0的钟差序列:{x(t0),x(t1),…,x(tN-1)},且ti=iτ0.经典的最小二乘二次拟合函数可表示为

x(t)=C0+C1t+C2t2+e(t),

(6)

式中:{C0,C1,C2}为拟合参数;e(t)为x(t)的随机变化分量。

为了简化参数估计,引入了切比雪夫多项式前三项作为内插函数来描述原子钟的确定性变化分量:

(7)

于是,二次内插函数可表示为

x(t)=q0Φ0(t)+q1Φ1(t)+q2Φ2(t)+e(t),

(8)

式中,拟合参数{q0,q1,q2}的单位与x(t)的单位相同,都为时间单位;而切比雪夫多项式Φi(t)(i=0,1,2)为无量纲的量。

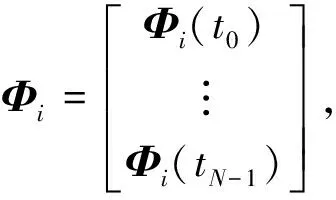
(9)

而切比雪夫多项式各项组成的矢量满足标准化正交特性,即ΦTΦ=[I3],其中,[I3]为(3×3)的单位阵。利用切比雪夫多项式的这一特性,可以简化参数估计,并可提高参数估值精度。根据式(8)可列出误差方程

V=Φq-L,

(10)

式中:Φ为N×3的系数阵;q为未知参数向量;L为钟差观测量x(ti)组成的列向量;V表示L的残差向量,有

(11)

假设钟差序列x(ti)独立等精度,那么未知参数向量q的最小二乘估值为

(12)

结合ΦTΦ=[I3],参数估值可表示为

(13)

(14)

结合式(6)、式(8),拟合参数{C0,C1,C2}可表示为

(15)

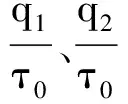
参数{C0,C1,C2}与参数{q0,q1,q2}之间的转换关系是很严格的,唯一的差异应归于截断误差。考虑到切比雪夫多项式的协方差矩阵是最优的,最小化了这种截断误差,因此,由上面的间接方法得到的参数{C0,C1,C2}估值精度高于用式(6)直接计算的参数估值精度。

3 灰色系统模型

灰色系统模型的实质是用指数函数作为拟合函数对时间间隔相等的钟差时间序列进行拟合,通过对原始钟差数据实行累加或累减使之成为具有较强规律的新数列,然后对此生成数列进行建模。具体过程如下:

设原始钟差数列为

x0(k)={x0(1),x0(2),…,x0(n)}.

(16)

对x0(k)作一次累加生成新数列

x1(k)={x1(1),x1(2),…,x1(n)}.

(17)

(18)

若将上式在区间[k,k+1]上积分,有

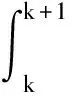
k=1,2,…,n-1,

(19)

而x1(k+1)-x1(k)=x0(k+1),因此,式(19)可以表示为

x0(k+1)=-aZ1(k+1)+u,

k=1,2…n-1,

(20)

式中,Z1(k+1)是x1(k),x1(k+1)两点的平均值:

k=1,2,…,n-1.

(21)

将式(20)用矩阵表示,有

(22)

(23)

(24)

对于一次累加生成数列x1(k),则有

(25)

式(25)是x1的预测函数,则原始钟差数据序列的预测值为

(26)

4 计算分析

为了分析不同预报模型的预报性能,分别利用4种钟差预报方法对BLOCK IIR-M卫星钟同一段数据预报1天和14天的钟差,IGS精密星历钟差精度优于1 ns,可作为真值,用于检验模型的预报效果。根据最小二乘法拟合多项式模型、切比雪夫多项式模型以及灰色系统模型的模型参数,建立相应的预报模型。

4.1 BLOCK IIR-M卫星钟预报1天结果与分析

对BLOCK IIR-M PRN17卫星钟1天的预报能力进行计算分析。PRN17的星载钟是Rb3原子钟。具体方案如下:

分别取1、7、14、21、35、42天的观测数据,来预报1天的钟差,计算结果如图1～6所示。

对于预报1天的情况,由上图1～图5、可以看出:

对于BLOCK IIR-M PRN17卫星钟,一阶多项式模型和切比雪夫一阶多项式模型除了14、35天的观测数据能取得优于20 ns的预报效果以外,其它天数观测数据均能取得优于5 ns的预报效果;二阶多项式模型和切比雪夫二阶多项式模型采用1天左右的观测数据能够达到约2 ns的预报效果,采用7天左右的观测数据能够达到约10 ns的预报效果;灰色系统模型采用1天左右的观测数据能取得约80 ns的预报效果。

4.2 BLOCK IIR-M卫星钟预报14天结果与分析

对PRN17卫星钟,根据不同天数的观测数据采用最小二乘法对钟差预报模型进行钟参数拟合,接着将预报了14天的钟差数据与真实值作差,计算结果如图7～图12所示。

对于预报14天的情况,由图7～图12可以看出:

对于BLOCK IIR-M PRN17卫星钟,一阶多项式模型和切比雪夫一阶多项式模型采用1天左右的观测数据进行预报时能够达到约10 ns的预报效果,采用7～42天左右的观测数据只能取得优于100 ns的预报效果;二阶多项式模型和切比雪夫二阶多项式模型采用7天左右的观测数据进行预报时能够达到约10 ns的预报效果,采用1天、14～35天左右的观测数据只能取得优于200 ns的预报效果;灰色系统模型采用1天左右的观测数据能取得约70 ns的预报效果。

5 结束语

通过以上的分析,对于BLOCK IIR-M卫星钟初步得出以下结论:

1) 利用多项式模型、切比雪夫多项式模型进行预报时,随着采用的观测数据量的增大,无论1天预报还是14天预报,预报效果不一定会好。

2) 在卫星钟差的1天预报中,一、二阶多项式模型和切比雪夫多项式模型比灰色系统模型能取得更好的预报效果,并且一阶多项式模型和切比雪夫一阶多项式模型的预报效果要稍微优于二阶多项式模型和切比雪夫二阶多项式模型的预报效果。

3) 在卫星钟差的14天期预报中,一、二阶多项式模型,切比雪夫多项式模型,灰色系统模型的预报效果相当;而且,在采用少量观测数据(1天左右)进行预报时,一阶多项式模型和切比雪夫一阶多项式模型的预报效果要明显优于灰色系统模型的预报效果;而灰色系统模型的预报效果要稍微优于二阶多项式模型和切比雪夫二阶多项式模型的预报效果。随着预报时采用的观测数据量的增加(7～42天左右),一、二阶多项式模型和切比雪夫多项式模型的预报效果要明显优于灰色系统模型的预报效果。

4) 灰色系统模型只需要采用少量的观测数据来建模,从而减少了数据量,提高了建模速度,而且所建立的模型在预报卫星钟差时,其精度有显著的提高。因此,该模型对于那些观测数据少,预报周期长的卫星,具有明显的优势。

[1] 朱凌凤.时间比对技术研究与原子钟性能分析[D]. 郑州:信息工程大学硕士学位论文,2006.

[2] 王宇谱,呂志平，孙大双，等.一种改进钟差二次多项式模型的导航卫星钟差预报方法[J].天文学报,2016,57(1):78-90.

[3] 王继刚,胡永辉,何在民，等. 基于修正线性组合模型的原子钟钟差预报[J].天文学报,2011,52(1):89-83.

[4] 张杰. 卫星钟性能分析及钟差预报[D]. 西安：西安电子科技大学,2013.

[5] 田婕. GPS/BDS原子钟性能分析及钟差预报模型研究[D]. 西安：长安大学, 2015.

[6] 张杰. 卫星钟性能分析及钟差预报[D].西安：西安电子科技大学,2013.

[7] 倚雷,熊永良,徐龙华. 两种GPS卫星钟差预报模型比较及精度分析[J],测绘地理信息, 2013(2): 17-19.