基于遗传算法的大学计算机基础自动组卷方法
2018-06-12杨春哲,常涵吉
杨春哲, 常涵吉


摘 要: 针对传统组卷方法效率、成功率低等难题,设计基于遗传算法的大学计算机基础自动组卷方法。首先设计大学计算机基础自动成卷适应度函数,采用编码对组卷过程中题型及与其数量分布相关的约束条件进行处理,然后设计选择算子、交叉算子以及变异算子,将适应度作为评价群体多样性的指标,求出交叉概率与变异概率,给出遗传算法终止条件。实验结果表明,该方法提高了大学计算机基础自动组卷方法的效率和成功率。
关键词: 遗传算法; 计算机基础; 自动组卷; 适应度函数; 约束条件; 编码
中图分类号: TN99?34; TP391 文献标识码: A 文章编号: 1004?373X(2018)11?0171?04
Genetic algorithm based automatic test paper generation
method of university computer foundation
YANG Chunzhe, CHANG Hanji
(Jilin Medical University, Jilin 132013, China)
Abstract: Since the traditional test paper generation method has the problems of low efficiency and low success rate, an genetic algorithm based automatic test paper generation method of university computer foundation is designed. The fitness function of automatic test paper generation of university computer foundation is designed. The coding is used to handle the related constraint conditions of question types and quantity distribution in the process of test paper generation. The selection operator, crossover operator and mutation operator are designed. The fitness is taken as the indicator to evaluate the population diversity. The crossover probability and mutation probability are solved, and the terminal condition of genetic algorithm is given. The experimental results show that the proposed method can improve the efficiency and success rate of automatic test paper generation method of university computer foundation.
Keywords: genetic algorithm; university computer foundation; automatic test paper generation; fitness function; constraint condition; coding
0 引 言
大学计算机基础自动组卷是实现在线考试系统的核心技术,当前很多学校机构都对自动组卷进行了大量研究,尽可能使最终形成的试卷达到用户要求,同时保证科学性[1]。在大学计算机基础题库试题质量要求高的情况下,自动组卷的效率和质量只和组卷方法有关。因此,设计一种科学有效的自动组卷方法非常關键,其涉及全局寻优问题,具有重要研究价值[2?3]。
当前常用的自动组卷方法有随机生成方法和回溯试探方法。随机生成方法通过随机抽取的方式从试题库中抽取试题,对其是否满足试卷要求进行判断,该方法有很高的不确定性,在试题数量多的情况下,效率极低[4]。回溯试探方法按照某一准则对当前组卷状态进行转换,试探性的选择试题破坏了选择试题的随机性,同时组卷所需时间长。为此,提出一种新的基于遗传算法的大学计算机基础自动组卷方法。
1 遗传算法的大学计算机基础自动组卷方法
1.1 大学计算机基础自动组卷模型
组卷问题可描述为:采用相应软件程序把成卷要求与资料库中试题特征参数匹配,得到符合成卷条件的试卷。组卷的目标为寻找最优解,确定最符合输入要求的组卷策略[5]。
在大学计算机基础自动组卷过程中,命题人会事先输入多个限制条件,主要含有以下几个方面:
1) 试卷总分:试卷的总分数,通过命题人设定;
2) 考试时间:学生参与试卷解答时间,通过命题人设定;
3) 试卷难易程度:通过难度系数体现,是学生关于试题失分状况的体现;
4) 试卷区分度:区分度为试卷对考生情况的辨识能力,通常大小为[-1,1],该值越大表示区分效果越好。一般情况下,当试题区分度高于0.39时,则认为试卷存在较好的区分度;当试题区分度低于0.2时,则认为试卷区分度很差。计算区分度采用的方法为:对分数进行排列,[Q1=27%×dh],[dh]表示高分组的难度,[Q2=27%×dl],[dl]表示低分组的难度,则区分度为[ξ=Q1-Q2总分数];
5) 试卷涵盖度:试卷中涉及知识点占所学课本的比重,是根据教学大纲与考试大纲设定的;
6) 试卷试题结构:试卷中包含的题型通常包括单选题、填空题、计算题、简答题等。
对上述组卷限制条件进行分析。试卷的涵盖度为最关键条件,在确定试题过程中,依据试题的知识点属性,通过考试大纲决定知识点在试卷中出现的形式和比重;试卷难易程度通过各考生分数情况确定,依据以往的测试结果对题库内各试题的难度级别进行划分,并赋予相应的难度系数值[6]。
通常要求全部考生的成绩服从正态分布,由于二项分布在一定条件下与正态分布类似,因此,本节通过离散型随机变量的二项分布体现试卷难度与分数的关系,公式描述为:
[Wsg=Fgswg1-ws-g] (1)
式中:[s]为正整数,表示最大难度级别;[Wsg]表示难度级别为[g]的试题总分数占整个试卷总分数的比例;[Fgs]表示难度级别为[g]的试题总分数;[wg]表示各难度级别的难度比例;[w]表示难度系数。
1.2 目标函数
设[k]为试卷试题数量,[Fz]为试卷总分数,按照二项分布试卷难度与分数的映射关系,通过难度系数求出每个难度级别的难度比例[wg],[T]为考试时间,[Tj]为各试题作答时间。设[PFN]为大纲内第[N]章知识点占试卷的比率,[M]为总章节数,[FN]为相应章节试题的分数,[ζj]为试题的区分度,则大学计算机基础自动成卷的初始目标函数如下:
[f=g=0swg-FgNFz+N=1MgFNFz-PFNs.t. T-j=1kTjT≤0.15j=1kζj×FNFz≥0.3] (2)
把考试时间与试卷区分度当成目标函数的约束条件,以减少运行时间。
1.3 遗传算法适应度函数的确定
依据上述目标函数确定适应度函数。适应度函数的复杂度为遗传算法复杂度的重要构成部分[7],因此,当设计适应度函数时需确保计算时间复杂度最低,把目标函数描述成计算最大值形式,保证适应度函数为非负函数。上述成卷的目标函数为求最小值函数,依据各函数特点,确定两函数间的映射关系为:
[f*=1(1+f)] (3)
式中: [f*]表示适应度函数;[f]表示目标函数。
针对任意个体,判断考试时间和试卷区分度是否符合约束条件,如果两者符合约束条件,则进行适应度计算;反之,停止计算。
1.4 遗传算法编码
通过基因分段式编码实现问题解的编码描述,采用编码对组卷过程中的题型及其数量分布相关的约束条件进行处理,由此实现问题的简化。详细编码过程为:先对每种题型进行独立编码,组成相应基因段,基因段的个数取决于题型的种数,这里用[K]描述;基因段中基因数取决于题库中此种题型的试题数量。若题库中存在[ε]道试题,则编码为[a1,a2,…,aε],其中:
[ai=1, 第i道试题被选中0, 第i道试题未被选中] (4)
对于被选中的全部试题需满足[i=1εai=k],[k]为试卷中的试题数量;被选中的每种题型试题需满足[i=1u1ai=b1,i=1u2ai=b2,…,i=1uKai=bK]。其中,[u1,u2,…,uK]表示題库内相应题型的试题数量;[b1,b2,…,bK]表示试卷中每种题型试题需要的数量。
1.5 遗传算子设计
遗传算子包括选择算子、交叉算子以及变异算子,下面对其进行设计。
1) 选择算子。在进行遗传选择时,通过最佳个体保存法与适应度比例选择法获取算子[8]。具体过程为:先挑出最好的个体,并将其复制至下一代中,然后根据每个个体被选择概率与其适应度间的函数关系实现剩余个体的挑选。求出被选择概率,其计算公式如下:
[P*i=Eii=1ZEi] (5)
式中:[Z]用于描述种群大小;[Ei]用于描述适应度。
2) 交叉算子。在进行交叉时,结合编码方案进行分析,选用单点交叉方式,交叉主要在同种题型组卷时进行。
3) 变异算子。变异算子能够实现局部检索,为辅助型算子,在初始种群形成时已符合各项约束条件。为了不改变约束条件,在同种题型中进行两点变异,也就是每种题型在自身编码段中进行变异。
1.6 自适应交叉与变异概率
交叉概率[po]与变异概率[pv]对遗传算法有极大影响,本节将适应度作为评价群体多样性的指标,使[po]与[pv]随适应度的变化而变化。依次求出交叉概率[po]与变异概率[pv]:
[po=λ1?Emax-EoEmax-E,Eo>Eλ2,Eo [pv=λ3?Emax-EvEmax-E,Ev>Eλ4,Ev 式中:[Eo],[Ev]表示被计算个体的适应度;[Emax],[E]分别表示上一代种群内个体最大适应度与平均适应度;[λ1],[λ2],[λ3],[λ4]均为系数,且[λ1=λ2=1],[λ3=0.2],[λ4=0.4]。 本文大学计算机基础自动组卷方法选择下述三种终止条件: 1) 搜寻到最优解,也就是出现用户满意的试卷; 2) 相邻两代最大适应度值的改变率低于阈值; 3) 达到既定进化代数。1.7 终止条件
1.8 自动组卷过程
基于遗传算法的大学计算机基础自动组卷方法详细实现过程如下:
1) 确定初始参数和初始群体,接收用户自动组卷请求;
2) 求出群体中不同个体的适应值,依据个体适应值和选择策略形成下一代父体;
3) 执行交换与变异操作,形成新一代群体,求出当前群体中不同个体的适应值;
4) 对新一代最优个体与上一代最优个体适应值进行比较,若降低,则用上一代最佳个体替换当前最佳个体;
5) 输出当前代数、最优目标函数值及最优个体编码,求出不同难度级别和分数等指标。
2 自动组卷实验结果分析
为了验证本文提出遗传算法的可行性与有效性,针对大学计算机基础课程,通过ASP+SQL Server 2000,依据遗传思想编写程序,进行自动组卷实验。假设题库共存在五种题型、六个章节、七个难度系数与四个认知层次。题库中有700题,其题型题量分布、章节题量分布、难度题量分布和认知层次题量分布情况如表1~表4所示。
假设组卷要求为:试卷总分为120分,选题需达到题型与题量要求,不同题型分数已给出。所有章节的分值误差、难度分值误差及不同认知层次分值误差都在±2分以内。详细要求如表5~表8所示。
自动组卷结果分析:
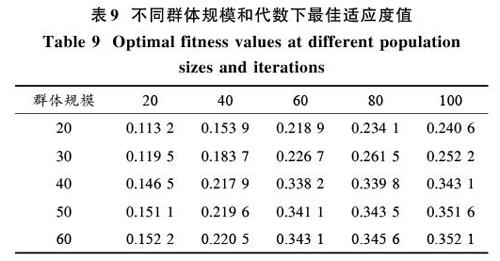
1) 在交叉概率为0.8,变异概率为0.1的情况下,令群体规模依次取20,30,40,50,60,运行代数在20~100范围内变化,则不同群体规模和代数下最佳适应度值改变情况如表9所示。
分析表9可知,群体规模对遗传算法收敛性有很大的影响。在群体规模较小的情况下(20和30),参与遗传算法的试题较少,搜索空间受到限制,适应度值小,得到有效试卷的机会很小。在群体规模达到40的情况下,适应度值明显升高,而当群体规模为50和60时,适应度值无显著区别,基本不增长,说明群体规模达到40时,即可达到收敛,而群体规模越大,则程序运行速度越低,所以本文实验设定群体规模为40。除此之外,还可以看出,在运行代数为60代的情况下适应度值已实现收敛,所以将运行代数设置为60代。
2) 令最大迭代数为60代,交叉概率为0.8,变异概率为0.1,群体规模为40。经50次调试运行,获取大学计算机基础自动组卷结果。为了验证本文方法的有效性,将随机生成方法和回溯试探方法作为对比,在题库量是700题的情况下,对三种方法的组卷时间、组卷成功率进行比较,结果如表10所示。
分析表10可知,本文方法成功概率为100%,且所需时间明显低于随机生成方法和回溯试探方法,性能优于其他两种方法,验证了本文基于改进遗传算法的大学计算机基础自动组卷设计与实现方法的优越性。
3 结 论
本文提出基于遗传算法的大学计算机基础自动组卷方法。介绍了大学计算机基础自动组卷模型,给出通过遗传算法实现大学计算机基础自动组卷的详细过程。经实验验证,所提方法效率和成功率较高。
参考文献
[1] 陈国彬,张广泉.基于改进遗传算法的快速自动组卷算法研究[J].计算机应用研究,2015,32(10):2996?2998.
CHEN Guobin, ZHANG Guangquan. New algorithm for intelligent test paper composition based on improved genetic algorithm [J]. Application research of computers, 2015, 32(10): 2996?2998.
[2] 吴爱婷,官伯然.一种基于遗传算法的超宽带天线自动设计方法[J].微波学报,2015,31(3):22?26.
WU Aiting, GUAN Boran. An automation design method of the ultra?wideband antenna based on the genetic algorithm [J]. Journal of microwaves, 2015, 31(3): 22?26.
[3] 李瑞森,张树有,伊国栋,等.可拓集成模式的工程图学试题库组卷方法研究[J].图学学报,2016,37(6):851?856.
LI Ruisen, ZHANG Shuyou, YIN Guodong, et al. Research on the test paper generating method of engineering graphics based on the extension and integration mode [J]. Journal of graphics, 2016, 37(6): 851?856.
[4] 王宁,蔡顺燕.基于随机相位重构的智能组卷混叠均衡算法[J].科技通报,2016,32(5):236?239.
WANG Ning, CAI Shunyan. Smart group aliasing equalization algorithm based on the random phase reconstruction [J]. Bulletin of science and technology, 2016, 32(5): 236?239.
[5] 席卫文,张春辉,王飞,等.一种基于改进遗传算法的医学题库自动组卷设计与实现[J].中国医学物理学杂志,2016,33(8):861?864.
XI Weiwen, ZHANG Chunhui, WANG Fei, et al. Design and implementation of improved genetic algorithm for automatic test paper generation [J]. Chinese journal of medical physics, 2016, 33(8): 861?864.
[6] 徐海东.基于遗传算法的自动组卷算法的研究[J].微型电脑应用,2016,32(3):60?62.
XU Haidong. Research on automatic test paper based on genetic algorithm [J]. Microcomputer applications, 2016, 32(3): 60?62.
[7] 吕海燕,周立军,宦婧,等.通用在线考试系统智能组卷遗传算法设计[J].计算技术与自动化,2016,35(4):85?90.
L? Haiyan, ZHOU Lijun, HUAN Jing, et al. Design of intelligent test paper generating genetic algorithm for common online examination system [J]. Computing technology and automation, 2016, 35(4): 85?90.
[8] 潘刚,杨清平,蒲国林,等.遗传算法在智能组卷系统中的应用研究[J].云南民族大学学报(自然科学版),2016,25(6):579?584.
PAN Gang, YANG Qingping, PU Guolin, et al. Application of the genetic algorithm in the intelligent test paper generation system [J]. Journal of Yunnan University of Nationalities (natural sciences edition), 2016, 25(6): 579?584.
[9] 杨秀霞,张晓锋,张毅.基于加速遗传算法的舰船电力系统故障恢复[J].电工技术学报,2005,20(5):53?57.
YANG Xiuxia, ZHANG Xiaofeng, ZHANG Yi. Shipboard power system service restoration based on the accelerated genetic algorithm [J]. Transactions of China electrotechnical society, 2005, 20(5): 53?57
