基于模糊RBF神经网络的分数阶滑模控制器优化设计

余潇 黄辉先

摘 要： 针对神经滑模控制系统中存在的对先验数据依赖性较强的问题，结合RBF神经网络的泛化能力和自学习能力以及模糊推理算法的强适应能力，提出基于模糊RBF神经网络的永磁同步电机分数阶速度控制系统。模糊推理的引入为神经网络的不确定性提供了有效的指导作用，同时，分数阶微积分算子的引入增加了传统滑模控制器的自由度，从而对该控制器进行了进一步的优化。仿真结果表明，相比RBF神经滑模控制器，提出的模糊RBF神经分数阶滑模控制器具有更好的控制性能。

关键词： 永磁同步电机； 滑模控制器； RBF神经网络； 分数阶； 模糊推理； 自由度

中图分类号： TN876?34； TM461 文献标识码： A 文章编号： 1004?373X（2018）11?0087?04

Optimization design of fractional?order sliding mode controller

based on fuzzy RBF neural network

YU Xiao， HUANG Huixian

（College of Information Engineering， Xiangtan University， Xiangtan 411105， China）

Abstract： Since sliding mode control based on neural network has the problem of strong dependence on prior information， the generalization ability and self?learning ability of RBF neural network and strong adaptability of fuzzy reasoning algorithm are combined to propose the fuzzy RBF neural network based fractional order speed control system of permanent magnet synchronous motor （PMSM）. The introduction of fuzzy reasoning provides an effective guidance for the uncertainty of the neural network， and the introduction of fractional?order calculus operator can increase the degree of freedom of the traditional sliding mode controller， so as to further optimize the controller. The simulation results show that， in comparison with the sliding mode controller based on RBF neural network， the fractional order sliding mode controller based on fuzzy RBF neural network has better control performance.

Keywords： PMSM； sliding mode controller； RBF neural network； fractional order； fuzzy inference； degree of freedom

0 引 言

永磁同步电机在机器人、数控机床、医疗设备等领域内得到了广泛应用，但受制于系统中的参数变化和负载扰动等因素，电机的转速控制性能受到一定的影响。滑模控制技术对系统内外部干扰所体现出的强鲁棒性为电机的高性能调速提供了一条有效途径，但考虑到滑模控制器的理想输出是高频切换的开关量，而运动控制系统中执行机构在时间上的延迟将导致系统状态在滑模面上的运动轨迹不会准确发生在设定的切换流形面，系统抖振将随之发生[1]，这无疑限制了滑模控制技术的应用范围。

国内外学者通过对抖振削弱方法的研究，获得了大量成果[2?10]。其中，文献[2?4]提出高阶滑模控制算法，但这种方法较为复杂，控制器的输出信号中存在着与其导数的耦合，不利于滑模控制律的设计；文献[5?7]依据干扰观测器对负载转矩进行观测，并设计出一类积分型滑模控制器对干扰进行抑制，但在这类方法作用下，系统的动态性能会受到一定的影响；文献[8?10]将智能算法引入滑模控制器的优化设计过程中，分别采用RBF神经网络和模糊推理方法整定滑模控制器的开关增益，但在这类方法作用下的系统中会存在静差。

本文综合考虑模糊推理算法和RBF神经网络在滑模控制器优化设计过程中的应用，利用模糊推理算法的强适应能力调整RBF神经网络中的权值，进而利用RBF神经网络来训练得出分数阶滑模控制器的实际输出量，达到了较好的综合控制性能。

1 永磁同步电机模型描述

永磁同步电机在两相旋转坐标系下的数学模型为：

[uq=Rsiq+λq+ωfλdud=Rsid+λd-ωfλqλq=Lqiqλd=Ldid+LmdIdfωf=npωr] （1）

式中：[ud，uq]是两相旋转d?q坐标系下的定子电压；[id，iq]是定子电流；[λd，λq]是定子磁链；[Rs]和[Ld，Lq]是定子电阻和电感；[ωf，ωr]是电机电角度和给定转速；[Lmd]是定子相电感；[Idf]是等效电流；[np]是磁极对数。

电磁转矩方程为：

[Te=Jωr+Bmωr+TL] （2）

式中：[Te，TL]是电磁转矩和負载力矩；[J]是转动惯量；[Bm]是摩擦因子。电磁转矩可描述为：

[Te=32npLmdIdfiq+Ld-Lqiqid] （3）

对于隐极式永磁同步电机，有[Ld=Lq]，此时式（3）可简化为：

[Te=kpiq=32npLmdIdfiq] （4）

将式（4）代入电磁转矩方程（2），可得：

[ωr=-BmJωr+kpJiq-1JTL] （5）

将式（5）转化为状态方程，可得：

[x=Ax+Bu+d] （6）

式中：[x=θωT]；[A=010-BmJ]；[B=0kpJ]；[u=iq]；[d=0-TLJ]。

将式（6）转换为离散状态方程为：

[xk+1=Axk+Buk+d] （7）

式中[xk=θkωkT]。

2 等效分数阶滑模控制器设计

定义式（6）中状态变量的误差及其变化率为：

[ek=θ?k-θk， dek=ω?k-ωk] （8）

式中：[θ?k]为位置指令；[ω?k]为位置指令变化率；[ek]为位置误差；[dek]为位置变化率的误差。根据式（8）可列出离散误差状态方程：

[xek+1=Axek-Buk+fk+d] （9）

式中：[xek=ekdekT；]

[fk=-θ?k-ω?k+θ?k+1BmJω?k+ω?k+1]。

定义切换函数为：

[sk=Cxek+Δζxek] （10）

由于：

[sk+1=Cxek+1+Δζxek+1=CAxek+C-Buk+fk+d+Δζxek+1] （11）

式中：[Δζ]为离散域下的分数阶微积分算子，可描述为：

[Δζxek+1=xek+1-j=1k+1-1jζjxek+1-j] （12）

式中：

[ζj=diagζjζjζj=1，j=0ζζ-1…ζ-j+1j！，j>0]

根据式（10）和式（11），可得：

[ueqk=-CB-1CA-Ixek+Δζxek+1+Cfk+Cd]（13）

式中：分数阶微积分算子中的阶次[ζ]的确定尚无系统的理论推导方法，本文通过反复测试，确定该值为[ζ=0.14]。据上所述，得出总的滑模控制律为：

[uk=ueqk+unk] （14）

式中[unk]为模糊RBF神经网络的输出。

3 模糊神经滑模控制器设计

模糊RBF神经网络中的信号传播及各层的功能如下：

1） 输入层

设定模糊RBF神经网络的输入为：

[xn1=sk，xn2=sk-sk-1] （15）

输入层的各个节点直接与输入量的各分量相连接，对该层的每个节点i，其输入输出关系表示为：

[f1i=xi] （16）

2） 模糊化层

模糊化层的每个节点具有隶属函数的功能，采用高斯函数作为隶属函数。则有：

[f2i，j=exp-f1i-cij2bj2] （17）

式中[cij]和[bj]是第i个输入变量在第j个模糊集合高斯函数上的均值和标准差。

3） 模糊推理层

模糊推理层通过与模糊化层的连接完成模糊规则的匹配，每个节点的输出为该节点所有输入信号的乘积，即：

[f3j=j=1Nf2i，j] （18）

4） 输出层

该层的输出为该层节点所有输入信号的加权和，则有：

[un=f4=W?f3=j=1Nwjf3j] （19）

式中[W=w1，w2，…，wNT]为模糊推理层和输出层之间的权重向量。

选取模糊RBF神经网络的学习指标为：

[Ek=12sk2] （20）

根据式（9）和式（10），则有：

[?sk?unk=-B] （21）

根据梯度下降算法，模糊RBF神经网络的权值学习方法为：

[Δwj=-?Ek?wj=-sk?Ek?unk?unk?wj=skBf3j]

[wjk=wjk-1+ηΔwj+αwjk-1-wjk-2]

[Δbj=-?Ek?bj=-sk?Ek?unk?unk?bj=skBwjf3f1-Cj2b3j]

[bjk=bjk-1+ηΔbj+αbjk-1-bjk-2]

[Δcij=-?Ek?cij=-sk?Ek?unk?unk?cij=skBwjf1-cijb2j]

[cijk=cijk-1+ηΔcij+αcijk-1-cijk-2]

式中：[η]为学习速率；[α]为惯性系数。

4 仿真分析

本文以Matlab软件为仿真工具，采用图1所示的仿真平台。永磁同步电机参数如下：[Rs=1.5 Ω，Ld=Lq=8.5×]

[10-3 H，np=4，J=2.5×10-3 kg?m2，Bm=0.8×10-3 N?m?s]。

输入信号采用正弦信號：[θ?k=0.5sin6πk]。模糊RBF神经网络结构分别选取为：输入层2个，模糊化层36个，模糊推理层36个，输出层1个。网络权值[W]的初始值选取为[-1，1]的随机值。学习速率和惯性系数分别选取为：[η=0.6，α=0.05]。为验证本文所提算法的优越性，基于RBF神经网络优化的滑模控制器用来进行对比分析。

5 结 论

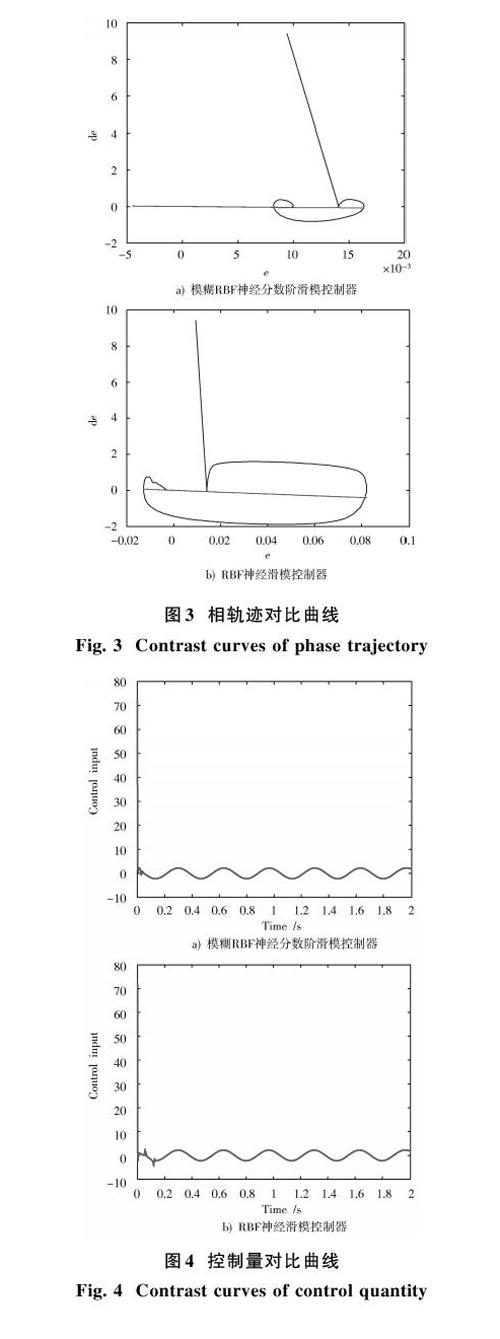
本文对模糊RBF神经分数阶滑模控制器的构建过程进行了详细论述，并给出了网络结构中各层之间权重系数、各节点的中心向量和基宽向量的更新方法。本文所提算法的优越性在与RBF神经滑模控制器的比较中得到了体现，仿真验证从转速响应、系统状态向滑模面收敛的轨迹和控制量三个方面展开。仿真结果表明，本文提出的算法具有较高的综合控制性能。

参考文献

[1] 高为炳.变结构控制的理论及设计方法[M].北京：科学出版社，1996.

GAO Weibing. Theory and design method of variable structure control [M]. Beijing： Science Press， 1996.

[2] 陈杰，李志平，张国柱.不确定非线性系统的高阶滑模控制器设计[J].控制理论与应用，2010，27（5）：563?569.

CHEN Jie， LI Zhiping， ZHANG Guozhu. Design of high order sliding mode controller for uncertain nonlinear systems [J]. Control theory and application， 2010， 27（5）： 563?569.

[3] BELTRAN B， AHMED?ALI T， BENBOUZID M. High order sliding mode control of variable speed wind turbines [J]. IEEE transactions on industrial electronics， 2009， 56（9）： 3314?3321.

[4] FRANCESCO D， ANTONELLA F. Higher order sliding mode controllers with optimal reaching [J]. IEEE transactions on automatica control， 2009， 54（9）： 98?104.

[5] 李政，胡广大，崔家瑞，等.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报，2014，34（3）：431?437.

LI Zheng， HU Guangda， CUI Jiarui， et al. Integral sliding mode variable structure control of permanent magnet synchronous motor speed control system [J]. Proceedings of the CSEE， 2014， 34（3）： 431?437.

[6] HAN H C. LMI?based sliding surface design for integral sliding mode control of mismatched uncertain systems [J]. IEEE transactions on automatic control， 2007， 52（4）： 736?742.

[7] 王丽梅，郑浩，贾启.永磁同步平面电动机的滑模控制器设计[J].电机与控制学报，2014，18（7）：101?106.

WANG Limei， ZHENG Hao， JIA Qi. Design of sliding mode controller for permanent magnet synchronous planar motor [J]. Journal of motor and control， 2014， 18（7）： 101?106.

[8] 刘治钢，王军政，赵江波.永磁同步电机神经网络自适应滑模控制器设计[J].电机与控制学报，2009，13（2）：290?295.

LIU Zhigang， WANG Junzheng， ZHAO Jiangbo. Design of adaptive sliding mode controller for permanent magnet synchronous motor neural network [J]. Journal of motor and control， 2009， 13（2）： 290?295.

[9] HSIAO M Y， Li T H S， LEE J Z， et al. Design of interval type?2 fuzzy sliding?mode controller [J]. Information sciences， 2008， 178（6）： 1696?1716.

[10] 逄海萍，江姝妍.伺服系统模糊滑模控制器的设计与仿真[J].系统仿真学报，2005，17（12）：2972?2974.

PANG Haiping， JIANG Shuyan. Design and simulation of fuzzy sliding mode controller for servo systems [J]. Journal of system simulation， 2005， 17（12）： 2972?2974.