计及整体可靠性与全过程费用的配电网规划模型及求解

云南电网有限责任公司瑞丽供电局 杨荣双 武汉大学电气工程学院 李燕

引言

随着国家新能源政策和电力体制改革的实施，大量分布式电源（DG）以多种形式接入配电网运行，系统的不确定性增加，配电系统规模不断扩大、结构日益复杂，配网自身可靠性问题日益严重。为了降低电力用户的停电风险，需要建立更全面的可靠性模型并且对规划的全过程进行统筹规划[1-2]。

首先，在配电网规划中可靠性指标计算时的线路故障模型多采用确定均值表示，但实际中概率指标计算更能反映真实情况，线路故障率会受多种因素影响。文献[3]分析了影响线路故障率分布的因素，考虑地理位置气候的影响，以及线路自身类型的影响，考虑这些影响因素建立规划过程中整体可靠性可以更加全面的反映配电系统的不确定性，并且可以有利于提高系统整体可靠性。

目前，配电系统规划模型已经有较完善的相关研究[4-20]，主要集中于促进分布式电源的最大接入容量或者提升DG的消纳能力，按规划内容可分为独立的网架规划、DG配置和网架与DG的协调规划。

文献[4]考虑到光伏出力的不确定性，建立DG优化配置模型；文献[5]考虑风速、光照强度和负荷间的相关性，建立DG选址定容模型；在此基础上，文献[6]建立了主动管理模式下DG选址定容双层规划模型；文献[7]利用解析法解决了给定DG容量时单条辐射线路上的DG最优配置问题，文献[8]对配网系统负荷节点功率及数量均固定时的DG优化问题进行了研究，文献[9]基于遗传算法优化DG总容量固定下的DG安装位置及容量，文献[10]以系统网损最优为规划目标处理DG并网时的选址定容问题，并结合改进粒子群算法及模拟退火算法对其进行求解。

首先，现有文献[11-19]没有很好的解决DG与网架两者的联合协调规划问题，然后，文献中[20-21]考虑的目标函数基本分为经济性、网损、运行、可靠性四类，并没有较完善的从配电系统规划过程全面的分析，因此建立统一的全过程费用目标对配网规划长期的经济效益有重要意义。

本文在建立考虑气候影响下的整体可靠性模型的基础上，首先利用典型风电、光伏及负荷的年时序场景集对系统不确定性进行描述，通过对规划各个阶段的分析，提出了全过程费用的配网规划模型，包含投资成本、运行成本、维护成本、故障成本、报废成本，并通过改进IEEE33节点系统进行仿真验证，本模型可以更全面的考虑配电系统的不确定性，在规划阶段对规划年限中全过程费用进行统筹规划，因此在配网规划年限较长时，能够获得较好经济效益。

1 输电线路不确定整体可靠性模型

配电网可靠性计算模型基本默认线路的故障率为常数，但实际其故障率所处气候环境等因素呈现非决定性，并且对配电系统可靠性计算有较大影响，因此借鉴输电系统可靠性计算方法，考虑气候不确定因素影响下对线路的规划年限中全过程故障率计算进行建模。

1.1 计及气象相关性的输电线路故障率分布模型

故障前工作时间分布模型主要是线路整个寿命周期内的结构老化模型，对于气象灾害的冲击作用而导致的短期强迫失效不具有适用性。

从气象对电网影响的周期性特征出发，用故障率依据历年相同月份故障时间统计计算方法，在获得各月故障率样本的基础上寻求全年总时间方向的故障率分布函数，得出时间相依的故障率数学模型，用以反映不同地区、不同电压等级、不同气象环境下的输电线路故障时间变化的规律，然后采用一次基波傅里叶函数来模拟输电线路故障率的逐月分布情况。

根据故障率的定义：

求取历史同期各月故障率公式如下：

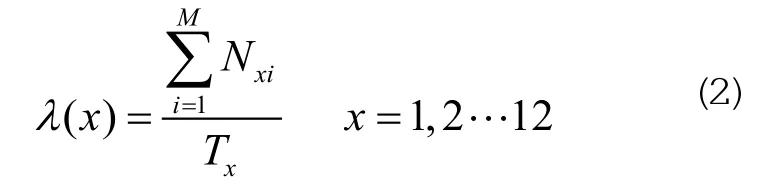
式中：λ(x)为历史同期第x月的故障率（次／月）；Nxi为第i年第x月中的故障次数；Tx为第x个月的时间；M为统计年数。

由于气象灾害年际爆发有差异，与气象环境相关的线路故障率在不同年份也有差异。尽管年度间有差异，但多年中历史同期的月份气象灾害导致的线路故障分布却基本不变。以某省典型的单峰与双峰模型为例进行说明。

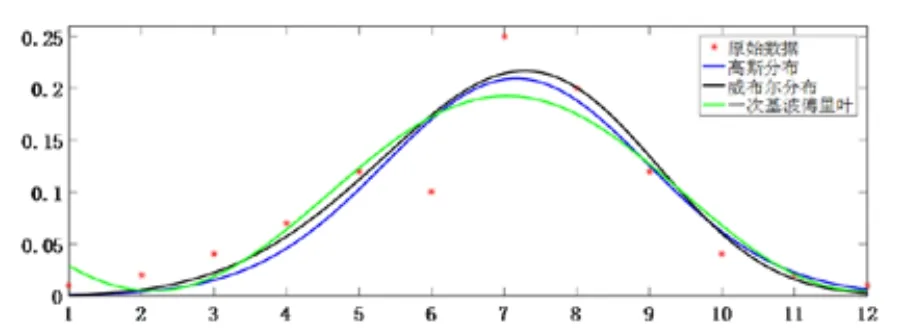
图1 某省线路故障率逐月分布及拟合曲线

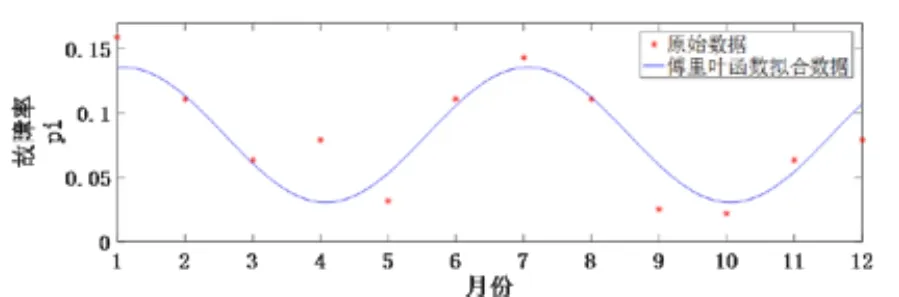
图2 某省线路故障率逐月分布傅里叶函数拟合曲线

1.2 输电线路全过程故障率分布模型

考虑气象对线路故障率的影响，建立线路使用寿命全过程的故障率分布模型，在前两节的基础上，将受气候影响的每年故障率规范化分布与该使用年限对应的线路故障率进行还原，得到输电线路该年限的故障率分布，进而得到线路的全过程故障率分布情况。

由于规划过程中，存在新建线路和待升级的线路两种类型的线路，两者之间的故障率有不同，因此如考虑规划的时间周期，则该周期内，以上面的单峰情况作为算例，将规划的第一年为例分析，新建线路与待升级线路的故障率分布去规范化如下表示。

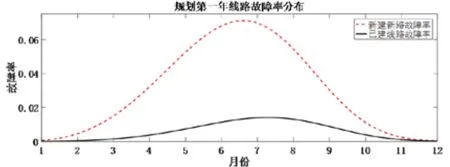
图3 规划第一年线路故障率分布

由图3可见，两者的故障率分布有明显区别，因此证明本模型的方法有一定的适用性，用该方法计算规划时间窗过程中的故障成本也更合理。

2 计及整体可靠性与全过程费用的配网规划模型及求解

2.1 不确定时序场景集的确定

场景集的选择是描述规划过程中不确定性的体现，负荷与DG的场景不确定性在规划过程中的原理是在基于目标函数中各场景赋予相应概率，从而得到优化解，模型如下：

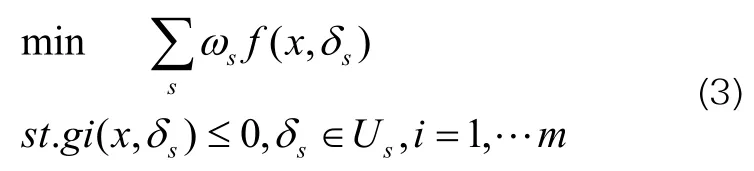
式中：ωs为场景s对应的概率值，Us与δs分别为场景s对应的不确定变量集合与变量，x为决策变量，ƒ为目标函数，gi为约束条件集合。

本文考虑适用性较大的典型时序法，并且可以保证负荷与DG纵向时间之间的相关性以及横向时间场景之间的时序性，因此，本模型采用四季的时序特性来描述DG出力和负荷功率，因此每个场景为等概率。

首先根据气象资料得到不同季节风速曲线和光照强度曲线，进而推算出风电、光伏出力以及负荷功率的时序曲线，并且对负荷的场景进行统计，以四季中每天24小时时间间隙为15分钟，风电与光伏出力场景选择如图4所示，负荷的场景见附录。

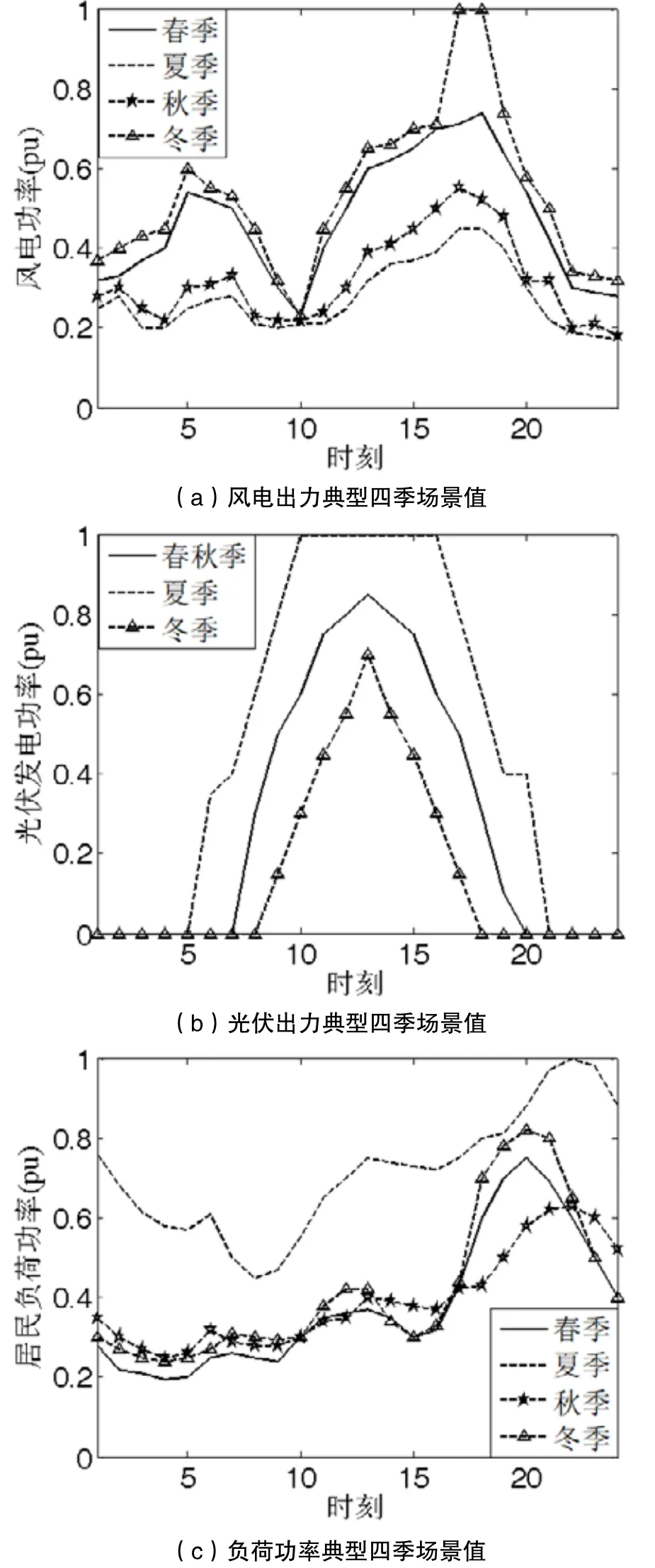
图4 典型不确定场景集合

2.2 目标函数

本文的全过程费用模型包含投资费用、维护费用、运行费用、故障费用、废弃费用。

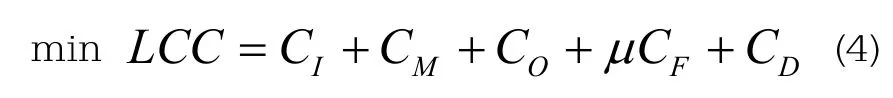
式中：CI为投资费用，CM为维护费用，CO为运行费用，CF为故障成本，CD为废弃费用。

投资费用包括新建与升级的线路总投资费用和新建DG的总投资费用

各分量的具体表达如下：

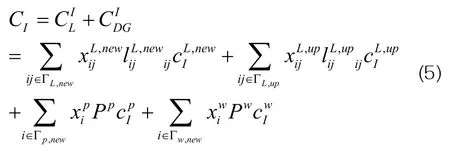
式中：ΓL,new、ΓL,up分别为线路新建与升级的集合，Γp,new、Γw,new分别为新建光伏与风电集合，为线路新建与升级的决策变量，为新建光伏与风电的决策变量，为新建或升级线路ij对应的长度，Pp、 Pw为新建光伏与风电的单位容量，为单位长度新建与升级线路对应的投资价格，为单位容量新建的光伏与风电的投资价格。

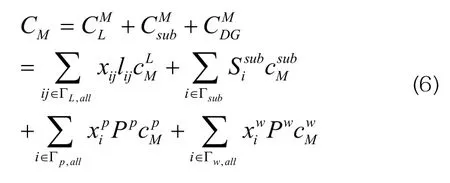
式中：ΓL,all、ΓP,all、Γw,all、Γsub分别为所有线路、所有光伏、所有风电、变电站集合，为单位长度线路的年维护费用，为单位容量光伏的年维护费用，为单位风电的年维护费用，为单位容量变电站的年维护费用。

运行费用包含网损费用，式中为线路ij在场景s下的网损值，ωs为场景s的概率，co为单位网损电量的价格。

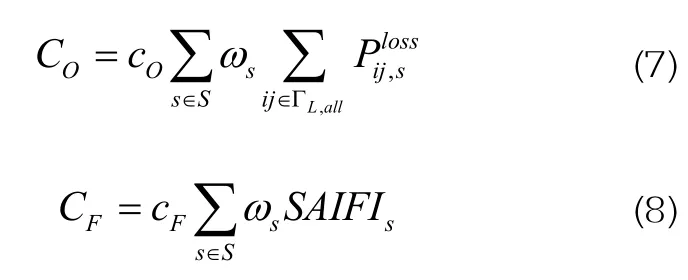
故障成本体现了系统的可靠性，SAUFIs为场景s下系统故障停电频率，cF为单位停电次数下的惩罚成本。μ为可靠性在目标函数中的权重值。

废弃成本主要考虑线路规划年限中的废弃成本，为单位长度线路的废弃处理价格。

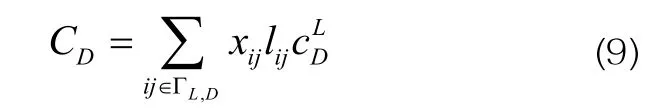
2.3 约束条件

约束条件主要包含容量约束、功率约束、节点电压约束。

（1）功率平衡约束

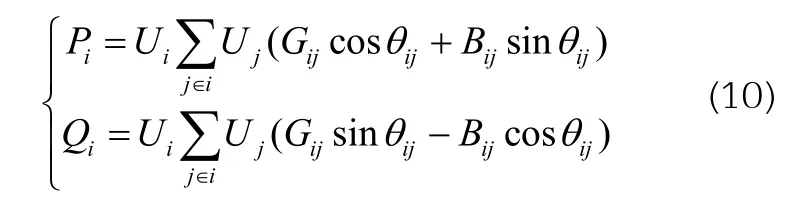
式中：Pi为节点i有功注入功率；Qi为节点i无功注入功率；j∈i为所有与节点i直接相连的节点集合；Ui为节点/电压幅值；Gü为节点导纳矩阵的实部；Bij为节点导纳矩阵的虚部；θü为节点i与j电压相角差。

（2）节点电压上下限概率约束

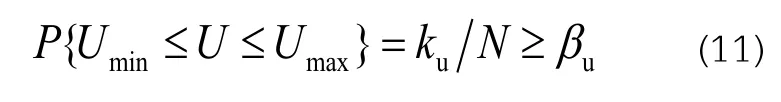
式中：Umax和Umin分别为节点电压的上限；ku为所有场景中满足电压上下限约束的场景数；βu为节点电压约束的置信水平。

（3）支路功率概率约束

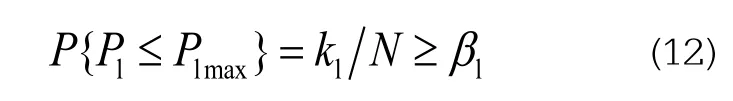
式中：P1为支路功率；P1max为支路允许的功率上限；k1为所有场景中满足支路功率约束的场景数；β1为支路功率约束的置信水平。

（4）分布式电源安装容量约

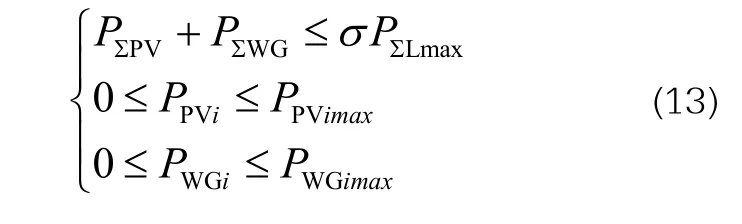
式中：P∑PV为PV总安装容量；P∑WG为WG总安装容量；σ为可再生能源DG最大渗透率；P∑Lmax为配网最大有功负荷的总和；PPVimax为待选并网节点i的PV最大安装容量；PWGimax为待选并网节点i的WG最大安装容量。

除这些等式约束和不等式约束之外，还需要满足配电网连通性和辐射状约束。

2.4 模型求解

本文采用粒子群算法求解模型，首先基于改进Kruskal算法构建最小生成树确定网络拓扑，粒子群决策变量在2.2与2.3模型中均已体现，采用十进制整数编码，具体求解流程与步骤如图5所示。

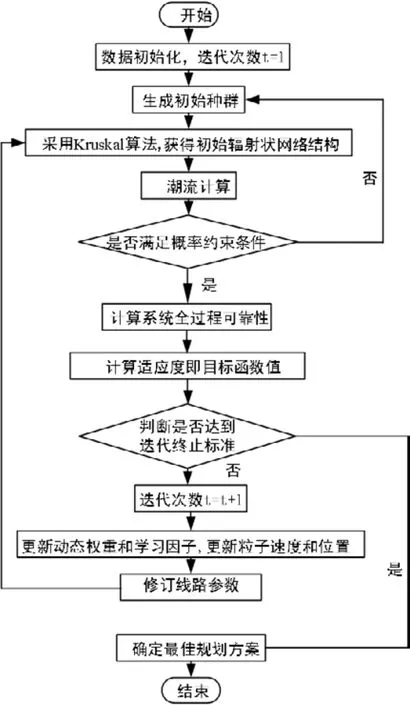
图5 模型求解流程图

3 算例分析

3.1 算例简介

改进IEEE33节点系统拓扑结构如图6所示，其中带括号的数字表示支路编号，不带括号的数字表示节点编号。

该系统包括61条线路、39个节点，其中新增负荷节点6个（节点34～39），待新建线路24条（支路38～61），待报废线路5条（支路3～7）DG的安装基准容量均为100千瓦，WG的待接入节点为3、6、16、27，每个节点WG安装个数上限分别为20、18、28、18；PV的待接入节点为8、10、28、30，每个节点PV安装个数上限分别为10、20、8、10。

原始线路参数为：单位造价6万/千米，单位阻抗为0.85+j0.42欧姆/千米，最大电流170安培。新建线路参数：单位造价8万/千米，单位阻抗为0.7+j0.52欧姆/千米，最大电流240安培。升级线路的参数为：单位造价10万/千米，单位阻抗为0.27+j0.38欧姆/千米，最大电流为380安培。线路单位运行维护费用率0.03。DG的单位电量PV和WG的投资费用分别为0.8和0.6万元/千米；单位电量PV和WG的运维费用分别为0.15和0.2元/千瓦时；单位电量的能源成本为0.4元/千瓦时。

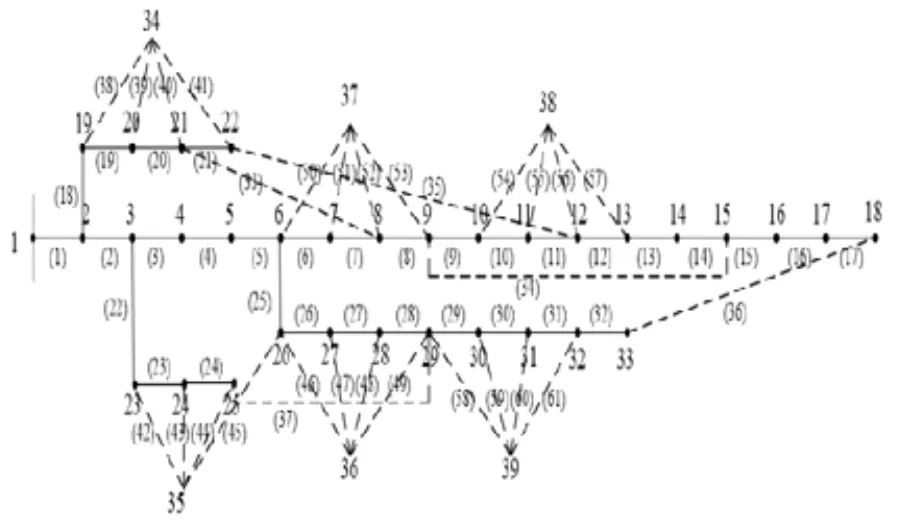
图6 改进IEEE33节点拓扑图

设置粒子群算法最大迭代次数为100次，种群大小为100个，惯性权重初始值及终值分别为0.9和0.4，学习因子c1和c2初始值分别为2.5/0.5，终值分别为0.5/2.5。

3.2 整体可靠性模型与均值可靠性模型规划结果

为验证本文整体可靠性模型，取目标函数中μ值为1，即故障成本与其余成本同等重要，将本文整体可靠性模型结果与采用确定性均值可靠性模型的规划结果进行对比如表1与表2所示。

Case1：整体可靠性全过程费用配网规划模型

Case2：均值可靠性全过程费用配网规划模型

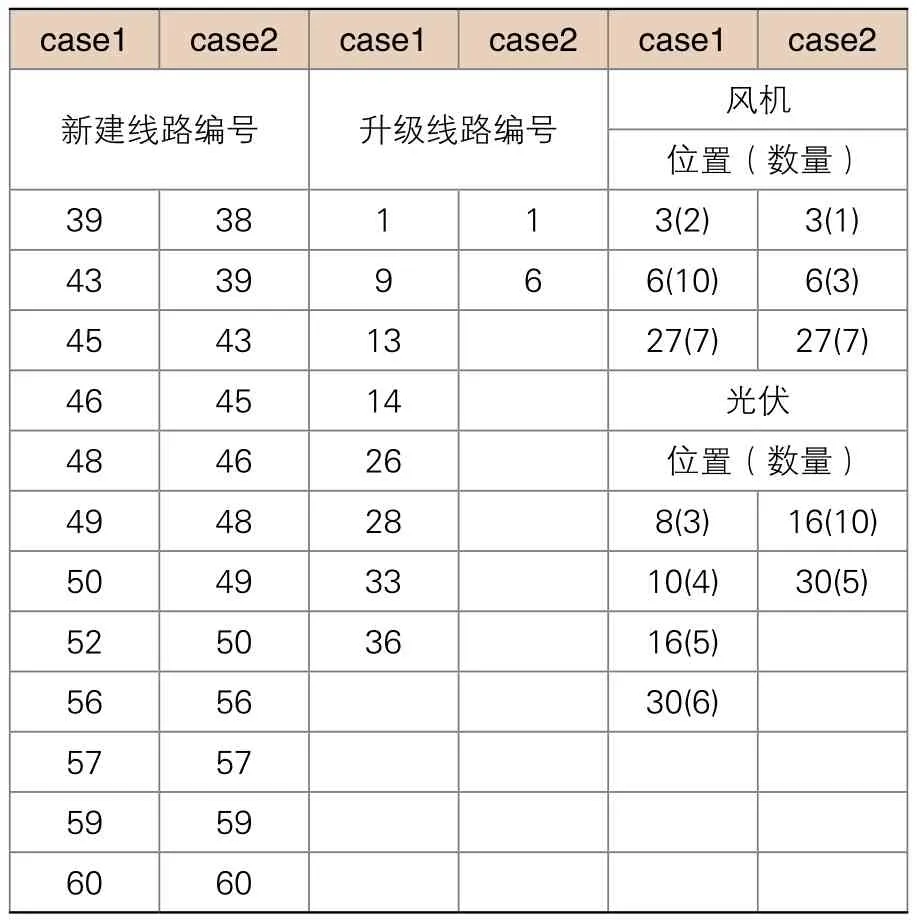
表1 整体可靠性与均值可靠性规划投资对比

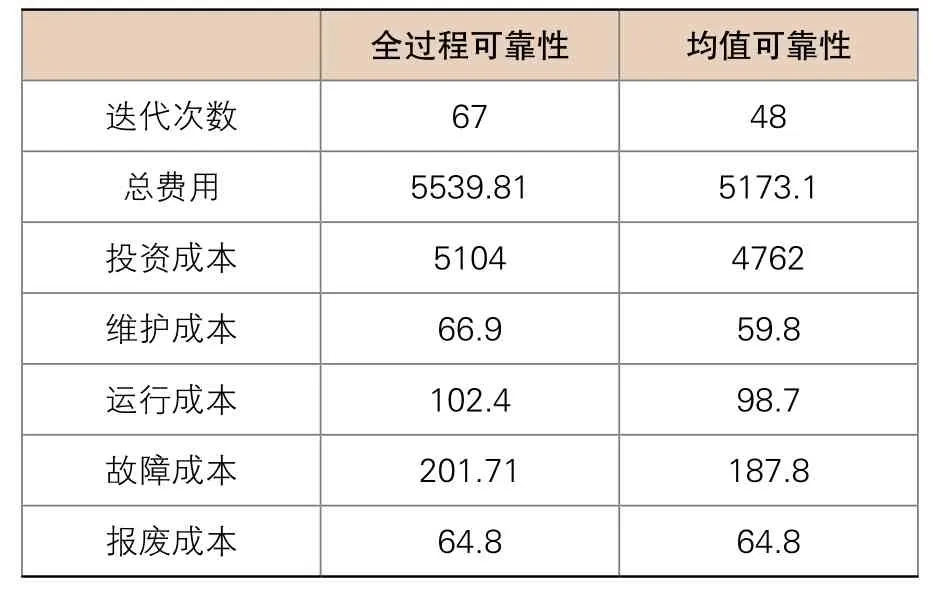
表2 整体可靠性与均值可靠性规划结果

由上述结果表明，本文的整体可靠性全过程费用配网规划模型成本较高，因为考虑气候影响下的全过程故障率增加了系统的不确定性，为减少故障惩罚成本，需要新建更多DG保证系统可靠性，因此系统中线路潮流更大，需要升级线路数量多，则投资成本更高，需要维护的设备更多，运行时网损比例更高，故障成本亦更高。并且迭代次数更多，不易收敛，均能表明考虑全过程可靠性模型更能反映系统的不确定性及必要性。

3.3 可靠性不同权重下配电系统规划结果

对于目标函数中μ值的选取，体现故障成本即可靠性在全过程费用中的重要程度，因此对不同等级的配网系统安全性要求不同时，可以对模型中的μ值进行更改或者提高故障惩罚系数，因此本文针对整体可靠性全过程费用配网规划模型中不同的μ值进行以下讨论。

不同权重μ配电系统规划投资对比如表3所示，不同权重μ配电系统规划费用对比如表4所示。

Case1：μ=1（3.2节Case1）

Case3：μ=2（安全性更高的配电系统）

Case4：μ=0.5（安全性较低的配电系统）

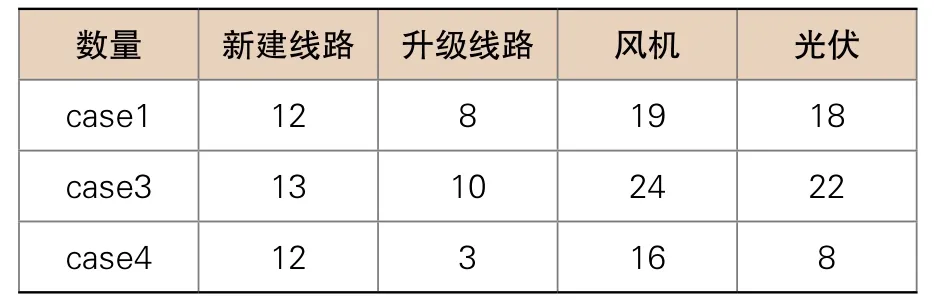
表3 不同μ权重 配电系统规划投资对比

由表3、4述结果表明，可靠性要求越高的配电系统规划结果的各项费用越高，需要有更充足的备用容量保证系统可靠性，以减小故障成本，表4中故障成本均为与μ相乘以后结果，因此可靠性成本实质随要求的提高而减少，也验证了本模型的适用性。

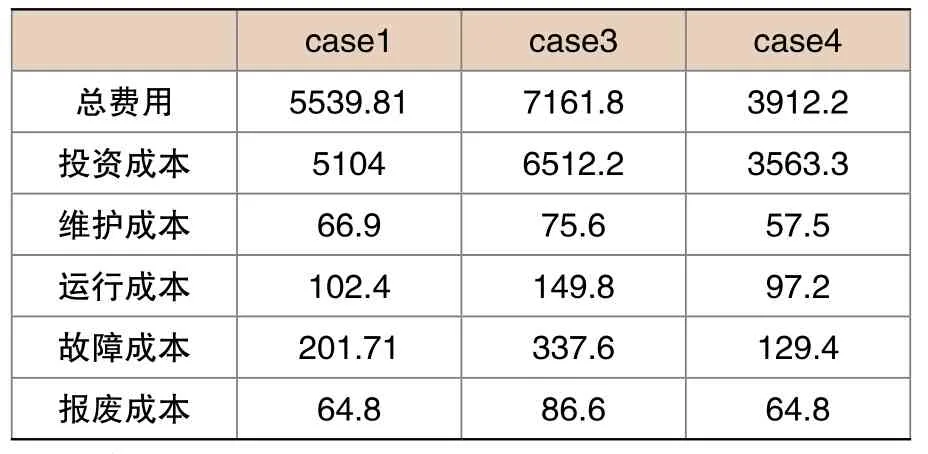
表4 不同权重 配电系统规划费用对比

4 结论

本文在建立考虑气候影响下的整体可靠性模型的基础上，通过对规划各个阶段的分析，提出了全过程费用的配网规划模型，包含投资成本、运行成本、维护成本、故障成本、报废成本，并通过改进IEEE33节点系统进行仿真验证，本模型可以更全面的考虑配电系统的不确定性，在规划阶段对规划年限中全过程费用进行统筹规划，因此在配网规划年限较长时，能够获得较好经济效益。

[1]Niwa M，Kato T，Suzuoki Y. Life-cycle-cost evaluation of degradation diagnosis for cables[C]//International Symposium on Electrical Insulating Materials.2005:737-740.

[2]左飞. 计及可靠性价值的配电网规划及其算法研究[D]. 重庆大学，2003.

[3]苏海锋，姜小静，梁志瑞. 考虑多种影响因素的配电网运行风险评估[J]. 电测与仪表，2014，51(6):34-38.

[4]Allan R N，Billinton R，Sjarief I，et al. A reliability test system for educational purposes-basic distribution system data and results[J]. IEEE Transactions on Power Systems，2002，6(2):813-820.

[5]Chowdhury N，Billinton R. A reliability test system for educational purposes-spinning reserve studies in isolated and interconnected systems[J]. Power Systems IEEE Transactions on，1991，6(4):1578-1583.

[6]谢开贵，周平，周家启，等. 基于故障扩散的复杂中压配电系统可靠性评估算法[J]. 电力系统自动化，2001，25(4):45-48.

[7]Haffner S，Pereira L F A，Pereira L A，et al.Multistage Model for Distribution Expansion Planning With Distributed Generation—Part I: Problem Formulation[J].IEEE Transactions on Power Delivery，2008，23(2):915-923.

[8]张李盈，范明天.配电网综合规划模型与算法的研究[J].中国电机工程学报，2004，24(6):59-64.

[9]李鑫滨，朱庆军.一种改进粒子群优化算法在多目标无功优化中的应用[J].电工技术学报，2010，25(7):137-143.

[10]Barbounis T G，Theocharis JB，Alexiadis MC，etal.Long-term wind speed and power forecasting using local recurrent neural network models[J]. IEEE Transactions on Energy Conversion，2006，21(1):273-284.

[11]Tascikaraoglu A，Uzunoglu M.A review of combined approaches for prediction of short-term wind speed and power[J]. Renewable & Sustainable Energy Reviews，2014，34(6):243-254.

[12]Troncoso A，Salcedo-Sanz S，Casanova-Mateo C，etal.Local models-based regression trees for very short-term wind speed prediction[J]. Renewable Energy，2015，81:589-598.

[13]臧宝刚.全寿命周期成本分析在变电站建设中的应用研究[D].华北电力大学(北京)华北电力大学，2011.

[14]Meyer C，Doncker RWD.LCC analysis of different resonant circuits and solid-state circuit breakers for mediumvoltage grids[J]. IEEE Transactions on Power Delivery，2006，21(3):1414-1420.

[15]程浩忠，张节潭，欧阳武，等.主动管理模式下分布式风电源规划[J].电力科学与技术学报，2009，24(4):12-18.

[16]Ouyang W，Cheng H Z，Zhang X B，etal.Distribution networks planning considering distribution generation by genetic algorithm combined with graph theory[J]. Electric Power Components and Systems，2010，38(3):325-339.

[17][26]Siano P，Chen P，Chen Z，etal.Evaluating maximum wind energy exploitation in active distribution networks[J]. IET Generation，Transmission & Distribution，2010，4(5):598-608.

[18]肖杰.全寿命管理理论在变电站建设项目设备选型中的应用研究[D].华北电力大学(北京)，2010.

[19]Pilo F，Celli G，Mocci S，etal. Multi-objective programming for optimal DG integration in active distribution systems[C]//Power and Energy Society General Meeting，2010 IEEE. Minneapolis，2010:1-7.

[20]Ochoa L F，Dent C J，Harrison G P. Maximisation of intermittent distributed generation in active networks[C]. IETCIRED Smart Grids for Distribution，Frankfurt，2008:1-4.

[21]Fan M T，Su A X，Zhang Z P. A planning approach for active distribution networks[C]//21st International Conference on Electricity Distribution，Frankfurt，IETServices Ltd，2011:1-4.

[22]Carmen L T B，Vinicius F M. Multistage expansion planning for active distribution networks under demand and Distributed Generation uncertainties[J].International Journal of Electrical Power & Energy Systems，2012，36(1):107-116.