面向悬挑式危岩体的非接触式测量技术

赵燕兵,李长安

(1.山西西山煤电股份有限公司 西曲矿,山西 古交 030200；2.中国矿业大学 力学与土木工程学院，江苏 徐州 221116)

对结构面的几何特征和结构面数据进行准确测量是岩体边坡的研究工作的基础[1]。但是在一些难以接触的结构面,控制面产状测量则显得十分困难。因此采用非接触式测量技术对难以接触的危岩体进行高精度测量是目前倍受关注的研究热点[2]。

文献[3]针对非接触式结构面提出了一种产状测量技术,并对测量技术的原理进行了详细阐述。文献[4]提出免棱镜全站仪应用在边坡岩体结构面测量的思路,并通过实验证明这种测量方法的有效性。文献[5]基于数字近景摄影技术实现了对岩体结构面的结构数据的快速采集。文献[6-7]将三维激光扫描技术应用在岩体结构信息采集中,并通过工程实例对这种测量数据采集方法的有效性进行了验证。文献[8]阐述了基于激光点云技术的岩体结构面数据全自动模糊群聚分析算法。

通过对上述研究成果的分析,可知准确建立坐标系和用合理的数学模型表示结构面产状式岩体结构测量的前提。因此,本文针对山西省古交市汾河北岸西曲矿某悬挑式危岩体的测量困境,使用TM50测量机器人实现对结构面的非接触式测量,并对测量数据进行修正,随后基于所测数据建立测量控制空间坐标系,通过空间坐标计算得出危岩体的关键测量要素。最后利用Sketchup软件[9]建立了危岩体的三维模型,直观展示了上述非接触式测量的可靠性。

1　研究区概况

研究区位于山西省古交市汾河北岸西曲矿，某悬挑式危岩如图1所示。危岩体上部距土层约0.5 m范围内呈中风化,下部呈微风化状态。危岩体规模较大,断面长约85 m,宽约21 m,走向为107°。此次研究主要以北西端的悬挑式危岩体作为主要研究对象。该部分危岩长43 m,宽约21 m,其上可见5条大型节理贯穿危岩体,对危岩体的稳定起控制作用。该区域常年降雨量充沛,岩体覆土流失严重,裂隙发育。该区域附近由于施工常有振动荷载,对危岩体造成扰动,存在潜在地质隐患。基于上述地质状况,不适宜进行直接测量。

图1　研究区的危岩体数字影像Fig.1　Digital photo of the dangerous rock mass

2　控制测量及测量原理

2.1　空间坐标系的建立

鉴于所研究的危岩体较为恶劣的地质现状,采用TM50测量机器人对危岩体进行边坡控制测量。边坡测量的对象是在危岩体边坡上按测量精度分布的控制点。利用测量机器人对测量控制点的空间坐标进行测量,为边坡建模提供数据支持。本文采用空间直角坐标系法进行坡面岩石控制点的测量[3]。通过测量机器人获取的控制点斜距、天顶距和水平方向值来计算得出控制点的三维坐标。测量空间坐标系的原点为测量机器人所在的测站点。X轴为过O的正北方向,Z轴为天顶方向,以右手法则建立空间直角坐标系,如图2所示[4]。

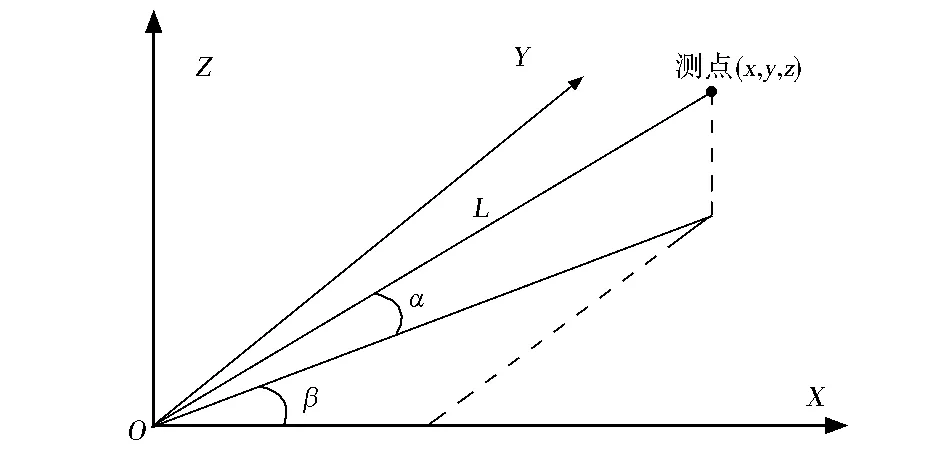
图2　空间直角坐标系的建立Fig.2　Establishment of space rectangular coordinate system

2.2　测量原理

结构面产状主要由倾向、走向和倾角三个要素决定。故在进行非接触式测量过程中,通过空间坐标计算得倾向及倾角即可,走向则由倾向±90°得到[10]。应用TM50测量机器人在岩体表面选取一系列不共线的特征点,进而利用空间向量计算得到结构面所在平面的法向量[11]。

2.2.1计算倾角

悬挑式危岩体的坡面上特征点是计算倾角的重要依据,将各特征点的坐标设为:A(a1,a2,a3),B(b1,b2,b3)及C(c1,c2,c3),且Li、αi、βi(i=1,2,3)为测量距离及对应的测量点与坐标系形成的夹角。

用空间直角坐标系中的参数来表示各点所设坐标,结果如下:

各点坐标可由上式所表示的结果得到。A,B,C三点为结构面上不共线的三点。故由上述坐标可得:

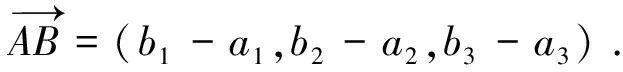
(1)

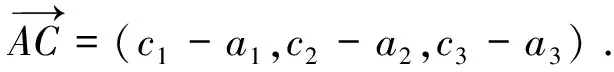
(2)

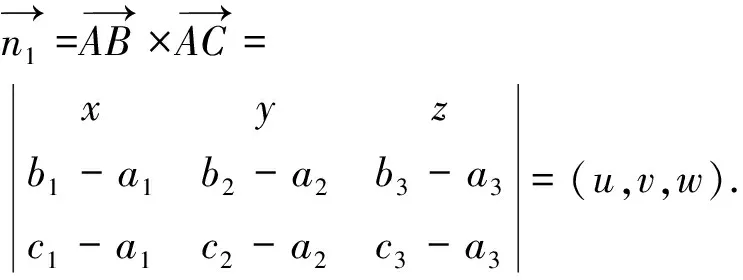
(3)

其中,

u=a2b3+a3c2+b2c3-a3b2-a2c3-b3c2,

v=a3b1+a1c3+b3c1-a1b3-a3c1-b1c3,

w=a1b2+a2c1+b1c2-a2b1-a1c2-b2c1.

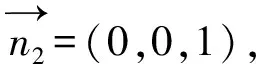
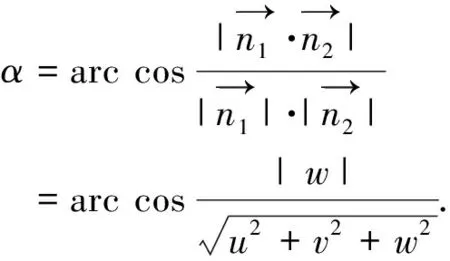
(4)

2.2.2计算倾向

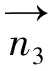
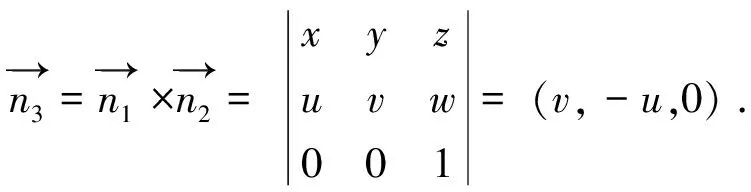
(5)

=(-uw,-vw,v2+u2) .

(6)

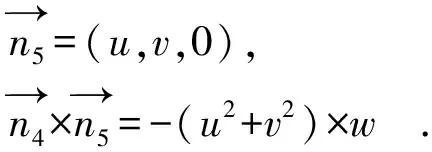
(7)

当u=0,v=0时,水平面与结构面平行;当u、v不全为0时,若w=0,水平面与结构面垂直。

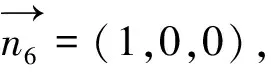
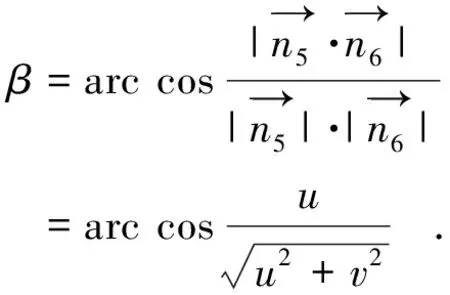
(8)

2.2.3计算走向

由走向和倾向的关系可以推出结构面走向为

γ=β′±90° .

(9)

3　控制测量及数据采集

3.1　工程坐标的建立

基于对所测危岩体面积以及坐标计算的要求,将测量空间坐标系设置为正北方向为X轴、天顶方向为Z轴。在完成全部控制点测量以及数据计算后,可在测量空间坐标系中计算得出结构面控制点、控制导线的坐标。

3.2　控制点的选取原则

结构面控制点的设置、测量的目的是实现对危岩体坡面的三维建模,因此选取的坡面控制点应满足以下要求。

首先控制点在坡面上的分布应该依据总体均匀、局部加密的原则。其次基于建模的数据要求,在全站仪成像重叠区域的绝对定向控制点不少于8个。最后控制点宜选取在坡面平缓处的明显连续颜色相似区域的边缘,避免裂缝、凹凸不平等局部地质因素影响棱镜测距的精度,以及方便后续图像处理中容易对控制点进行定位[12]。此外控制点与全站仪在结构面的不正交的最大偏斜小于30o,以提高测效率。

由于TM50测量机器人的图像放大倍数和图像比例可能存在差别,以及岩体色度具有随机性,不利于后续图像处理的精确度,因此在控制点选取中尽量不选取坡面面积较小的颜色相近区域的中心作为控制点[12]。

在控制点成像过程中采用中心快速成像法,以提高控制点的定位效率。该方法在控制点确定后,快速对控制点为中心的小区域进行图像记录,这样在后期图像处理中能够依据这些图像记录快速定位控制点,提高图像处理效率[13]。

3.3　控制点的坐标测量

依据上述原则,选取首级控制点,如表1示。

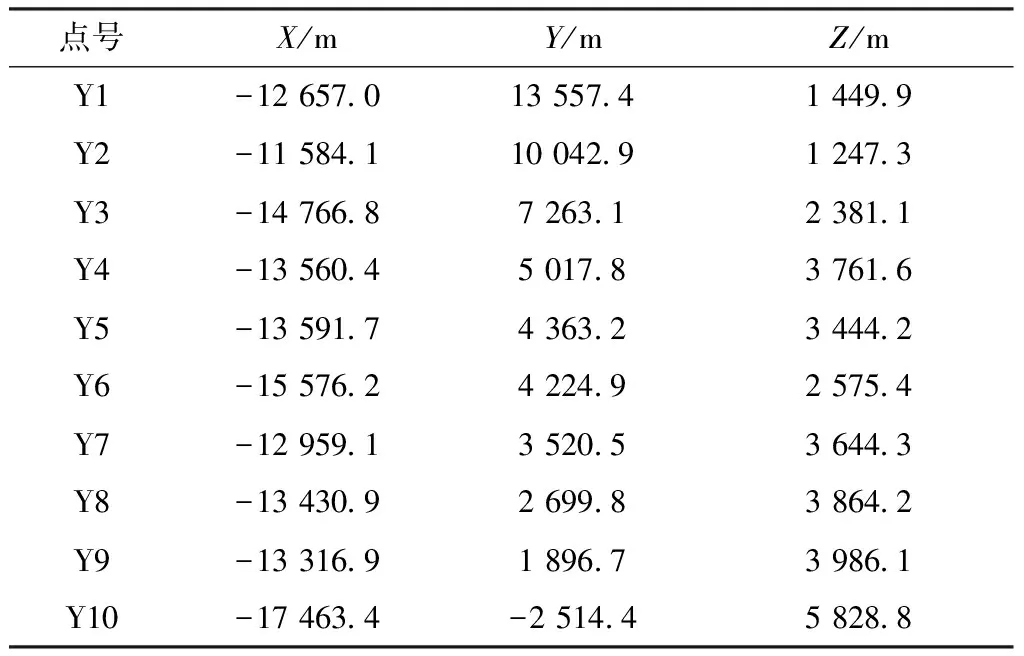
表1　首级控制点坐标Table 1　Primary control point coordinates

由于危岩体地质条件的限制,坡面次级控制点采用免棱镜模式进行测量。将测量机器人设置在控制导线点上,输入测点坐标和仪器高度,以该控制导线定向,采用免棱镜模式完成对次级控制点的测量[5]。完成测量后,在测量空间坐标系对测量数据进行坐标转换,得出次级控制点的坐标,如表2所示。

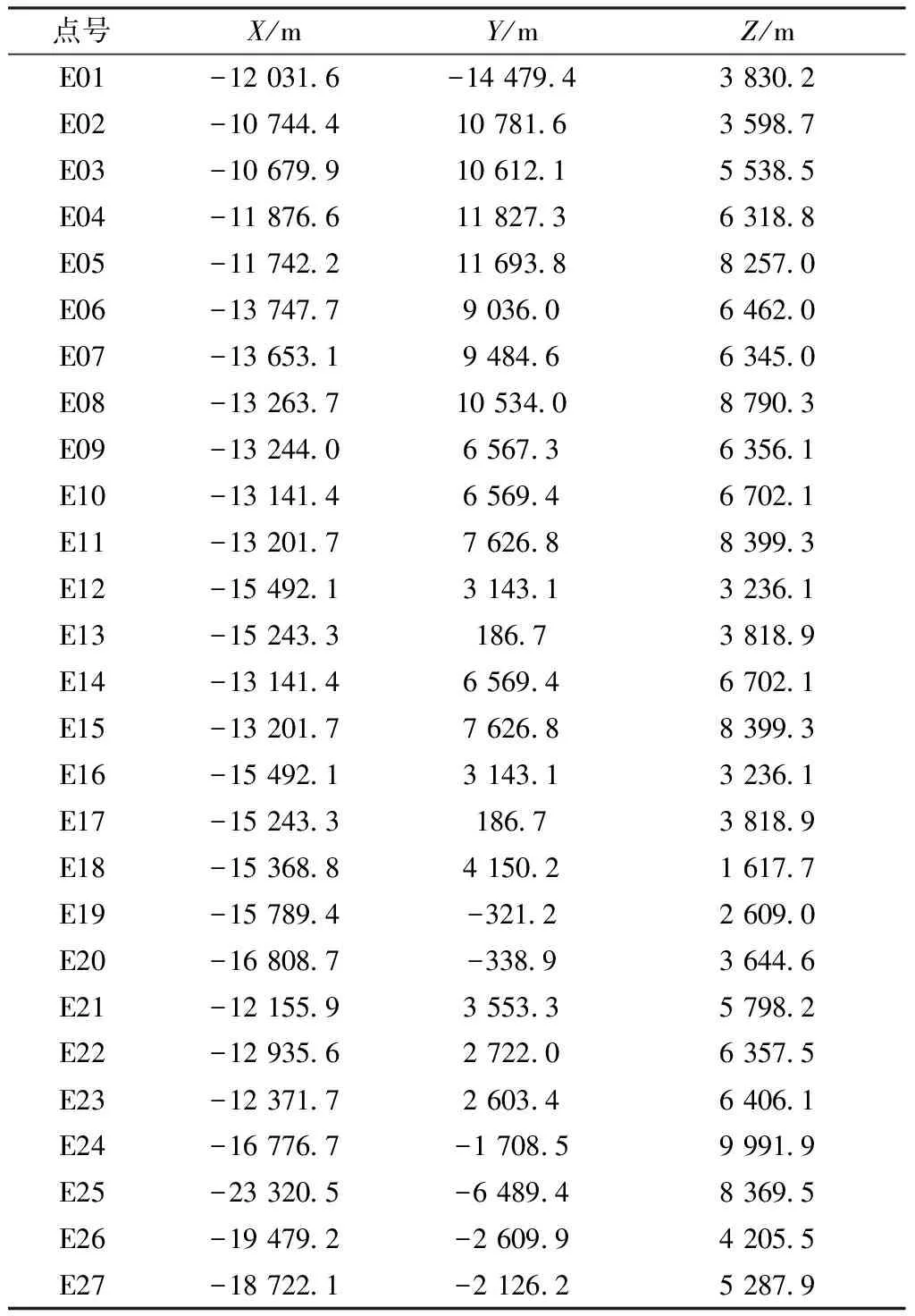
表2　次级控制点坐标Table 2　Secondary control point coordinates

4　数据处理与修正

由于测量仪器存在的误差,基于提高测量精确度的考虑,需要对测量误差进行修正。

4.1　数据采集

TM50测量机器人能够基于内部程序软件控制实现对测量过程的自动控制。为了降低一次设站的测回间的气象误差,要求一次设站的测回数和方向数都低于规范要求,并对测量仪器的精度和测速提出较为严格的要求。

目前徕卡测量机器人TM50能够完成自动照准目标的基础上,完成满足规范要求的快速、准确的测量。因此只需要依据测量时的气象条件对仪器测量值进行修正。

测量中,仪器的读值为标准气象条件下的测量值,需要依据现场气象条件进行修正。修正方法是,首先对观测过程中所有测站的仪高、镜高以及气象元素进行观测和记录。然后在数据处理时结合观测标志间的高差、仪器高、棱镜高进行修正。测量数据的相关技术指标如表3和表4所示。

表3　距离观测技术要求Table 3　Technical requirements for distance measurement

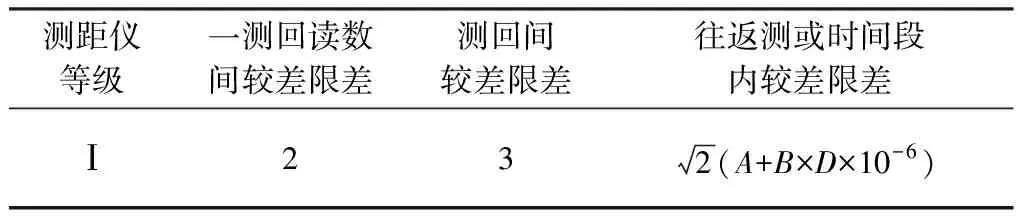
表4　距离测量的较差限差Table 4　Poor limit error of distance measurement

4.2　数据处理

4.2.1气象修正规范

电磁波测距主要受到空气折射率的影响,因此气象修正的主要目的是基于测量时的空气折射率对基于电磁波测距仪器的实际读值进行调整。根据相关研究成果,空气折射率n与气压、空气温度、空气湿度存在可确定的相关性,其计算公式为:

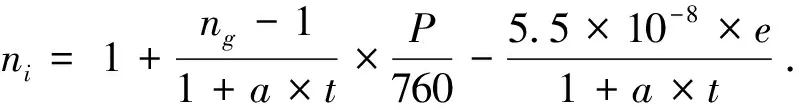
(10)

式中:P为实际气压,mmHg;e为实际水汽压,mmHg;a为大气膨胀系数,1/273.16;t为空气的干温,℃;ng为标准气象条件下调制光的折射率。其计算公式为:

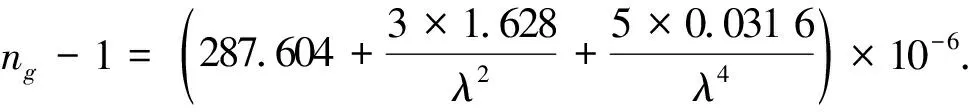
(11)

式中:λ为单色光的波长,μm。气象修正按下式计算:

VD=D′×(ng-ni)×10-5.

(12)

式中:D′为观测距离,m。

4.2.2周期误差修正

当测距精度要求较高,且振幅值不小于仪器固定误差的1/2时,对测量距离进行周期误差修正,单位为mm。

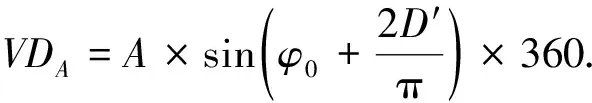
(13)

式中:A为周期误差的振幅,mm;φ0为周期误差的初相角,(°)。

4.2.3仪器常数修正

仪器加常数、乘常数等系统误差可通过检定确定,并在数据处理中加以修正。对加常数的修正公式为:

VDK=K.

(14)

式中:VDK为加常数修正值,mm;K为加常数,mm。

对乘常数的修正值公式为:

VDR=R×D′.

(15)

式中：VDR为乘常数修正值，mm；R为乘常数，mm/km；D′为观测距离，km。

4.2.4斜距改平

控制导线边长测量时每次设站的仪高都存在差距,因此需要对斜距测量值转换成水平距离并换算到相同高度的参考平面上才能进行对比。

倾斜改平的方法有对向三角高差法和等级水准测量测定法。其中对向三角高差法对测距端点的高差和三角高差有明确要求,而等级水准测量测定法对其高差的范围具有较强的适应性。因此采用后一种方法进行倾斜改平。

对观测距离D′的测量值进行气象修正后,依据下式对测量距离进行改平计算:

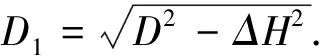
(16)

由于测量得出的水准高差包含仪器中心与棱镜中心的斜距,因此式(16)中ΔH是水准高差的测量值和仪器高与测量控制点高度的差值之和。水准高差、仪器高、测量控制点高之间关系图如图3所示。

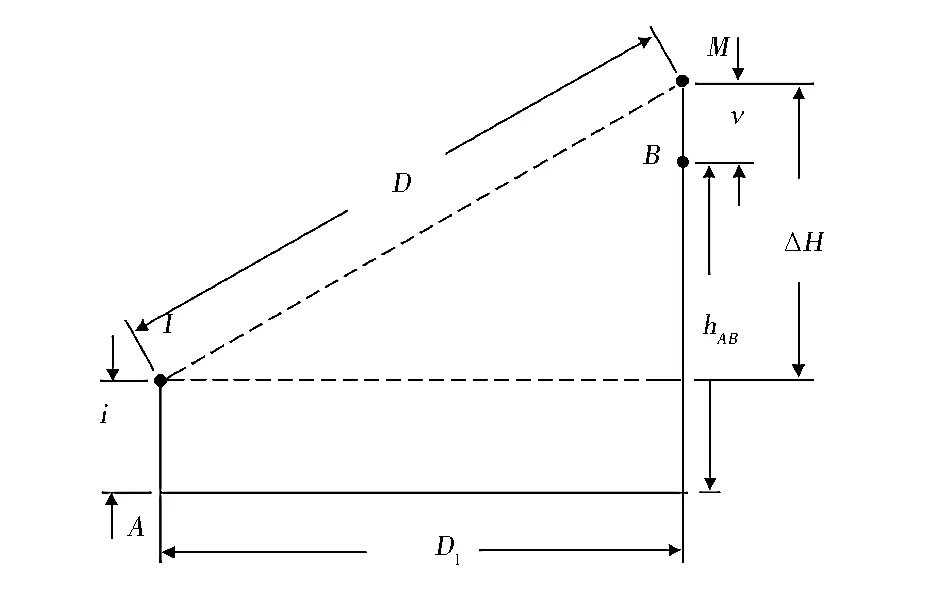
图3　水准高差、仪器高、测量控制点高示意图Fig.3　Diagram of level difference, equipment height, and control point height

图3中,i和v分别表示仪高和测量控制点高度。hAB表示水准点A和B之间的高度差，为斜距改平后的高差。D为修正后的斜距。

已知i和v,高差ΔH有如下关系式:ΔH+i=hAB+v;已知A、B点的高程HA、HB,ΔH计算公式为:

ΔH=HB+v-(HA+i).

(17)

5　建立模型

5.1　建模过程

本次建模的主要流程如下:

首先运用TM50非接触式测量仪测量出的危岩体的某些特征点(裂隙、岩层表面转折点等[14]),同时手绘危岩体表面草图,并标示出每一个点的大概位置。其次将所测的数据点导入到CAD中,参考数字摄影图以及手绘草图,将各个数据点连接成线,保存并导出DWG格式的文件。然后将导出的DWG格式的文件用Sketchup打开,并进行进一步的处理,勾勒模型的大致轮廓。由于Sketchup本身对模型的细节处理有限,将Sketchup所建的危岩体轮廓保存为3Ds文件,并用专业的建模软件3DsMAX进行细节化的处理，再导入至Sketchup中进行渲染、观察。最后再去现场,利用MS60全站扫描仪扫描危岩体表面,测得危岩体表面的点云图,并用逆向工程软件Geomagic将点云图建立成模型,与之前的模型进行对比观察,同时利用点云图大数据的优点拟合危岩体出露结构面,并解译其中的相关数据[8]。

5.2　影像与模型对比

由模型与数字影像对比可见非接触式测量获得的数据具有可靠性。该悬挑式危岩体的稳定性主要由5条贯通裂隙控制,其中三条在中部切割形成楔形体,且楔形体已经碰落,可见岩面明显比坡面整体新鲜。

图4所示为利用MS60非接触式测量仪所建立的模型。

图4　悬挑式危岩体点云图模型Fig.4　Point cloud model of overhanging dangerous rock mass

图5所示为TM50非接触式测量仪所建立的模型。

图5　悬挑式危岩体模型成果Fig.5　Modeling result of overhanging dangerous rock mass

6　结论

本研究针对传统接触式测量难以解决的悬挑式危岩体的高陡边坡、高空结构面等远距离或难以接触的结构面测量困难的问题,提出一种非接触式的测量方法。该测量方法运用了空间向量原理在笛卡尔空间右手坐标系对控制点测量数据进行了空间坐标转换,指出了坡面控制点整体分布和局部点位选取原则,研究了基于气象条件的测量数据的分析修正方法。最后通过对危岩体的三维建模,较直观地体现本文所述测量方法的精度和有效性。