利用多变量GM1,N灰色模型预测运动成绩的研究
2018-06-11谢晖
谢晖


摘 要:运动成绩因受多种因素的共同影响,其排列有不规则且非线性的特点,导致GM(1,1)模型实际预测时频频失效,预测结果与原始数据有较大偏差。而GM(1,N)模型具有可通过因子变量矫正主行为变量的固有特性,可有效拟合此类不规则且非线性曲线,提高运动成绩的预测精度。本文首先给出建立GM(1,N)模型预测运动成绩的方法,后以奥运会和世锦赛男子200米冠军成绩为例,建立了基于多因子变量的GM(1,N)预测模型。通过实际计算证明了GM(1,N)模型的拟合精度和预测精度均高于GM(1,1),充分的说明了GM(1,N)模型更适宜进行成绩预测工作,并在此基础上分析了GM(1,N)模型预测运动成绩时的优势及注意事项。
关键词:灰色系统 GM(1,N)模型 成绩预测 拟合精度 预测精度
中图分类号:G80 文献标识码:A 文章编号:2095-2813(2018)05(a)-0221-05
灰色系统理论是研究少数据、贫信息不确定性问题的方法[1],在体育领域中主要被用来进行成绩预测等方面的研究[2-5]。近几年人们主要是应用灰色系统理论中的GM(1,1)模型对运动成绩进行预测,并较好的完成了预测任务,为决策者在制定训练计划、战略目标等方面提供了重要依据[6]。但在实践中发现,GM(1,1)模型的预测效果有时较好,有时则会出现较大偏差。究其重要原因是,运动成绩受多个变量,多种因素的影响,是运动员竞技能力、比赛发挥等多种因素综合作用的结果,与比赛对手、场地器材等均有一定关系[7],因此仅利用一项赛事中前几届的成绩来预测未来该赛事成绩的方法是有待商榷的。现实体育运动中,尤其是在短距离竞技比赛中,成绩分布往往只在分秒之间,因此如何提升预测的精准度是我们现在亟需解决的问题。
GM(1,N)灰色模型实质为多变量一阶微分方程,较GM(1,1)模型其优势在于可对多因子的系统作整体的、全局的、动态的分析,能更好地揭示系统的内部规律[8-9]。运动成绩显然属于一个多因子复杂系统,需对其进行整体、全局、动态的分析,而GM(1,N)模型因其包含多因子变量特点,可有效满足该需求。基于上述分析,本文在GM(1,1)灰色预测模型的基础上成功引入多个变量,生成了GM(1,N)模型,并探讨了GM(1,N)模型在运动成绩预测中的可行性。
1 运动成绩预测中的GM(1,N)模型
1.1 GM(1,N)模型原理
1.2 GM(1,N)模型相关变量的选取
GM(1,N)模型中的行为变量1作为被预测的对象,称为模型的主数据,有且只有一个。而对行为变量产生影响的因子变量被称为i辅数据,可以有多个。在选取行为变量建立GM(1,N)模型时,首先应考虑辅数据与主数据之间的相关系数,||若大于0.3,则说明主数据与辅数据为显著性相关,可以进行建模;反之则应舍弃该辅数据。
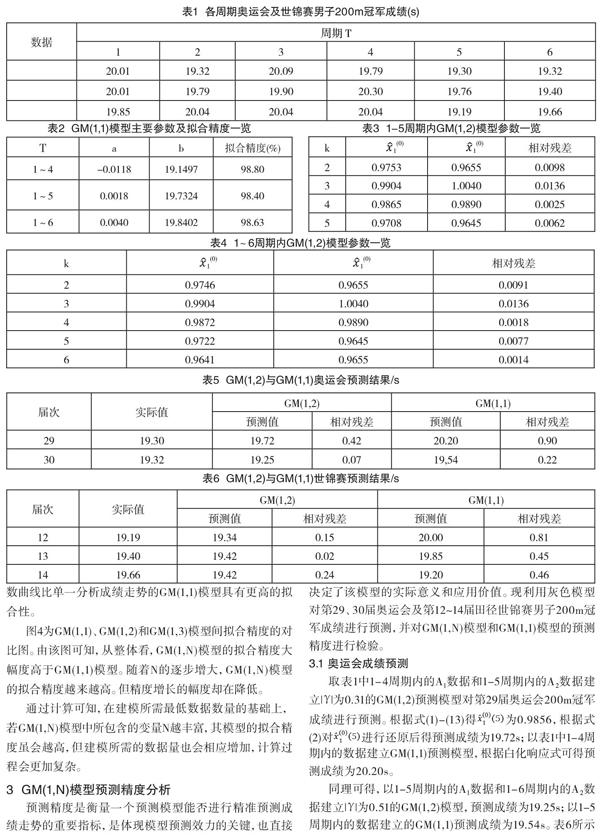
当选取周期为1-5的数据建立GM(1,2)模型时,其拟合精度为99.18%,模型参数如表3所示。当选取1-6周期内的数据时,其拟合精度为99.31%,参数如表4所示。
在GM(1,2)模型的基础上,加入在三个周期下与表1中A1数据相关系数||分别为0.4、0.51和0.54 的A3数据,作为因子变量3,同理可建立GM(1,3)模型。需要说明的是,本例中A3为奥运会后一年世锦赛的成绩,在预测奥运会成绩时并没有实际意义。因此本文只将其作为相关因子变量建立GM(1,3)模型,与原始数据进行拟合度检验而不直接参与奥运成绩预测工作。
利用GM(1,3)模型进行预测最低所需14个数据,即当行为变量1只有4个数据时,模型的函数曲线与原始数据重合,勉强可以预测。通过计算可得该模型在三个周期下的拟合精度分别为100%、99.67%和99.57%。
2.3 GM(1,N)与GM(1,1)模型拟合精度的比较
依据上文所得数据,对两个模型的函数曲线进行比较后发现,GM(1,N)预测模型可以比GM(1,1)模型更好的拟合原始数据,比较结果如图1至图3所示。
由图1至图3可以看出,由于GM(1,1)模型中只包含一个自变量,其函数为一直线,较适合预测有规则且趋势唯一的数据;而运动成绩为不规则波动数据,因此利用GM(1,1)模型进行预测往往会出现较大误差。事实证明,现实生活中影响运动成绩的因素远不止一个,所以利用可以将多种影响因素进行综合分析的GM(1,N)模型进行成绩预测,其函数曲线比单一分析成绩走势的GM(1,1)模型具有更高的拟合性。
图4为GM(1,1)、GM(1,2)和GM(1,3)模型间拟合精度的对比图。由该图可知,从整体看,GM(1,N)模型的拟合精度大幅度高于GM(1,1)模型。随着N的逐步增大,GM(1,N)模型的拟合精度越来越高。但精度增長的幅度却在降低。
通过计算可知,在建模所需最低数据数量的基础上,若GM(1,N)模型中所包含的变量N越丰富,其模型的拟合精度虽会越高,但建模所需的数据量也会相应增加,计算过程会更加复杂。
3 GM(1,N)模型预测精度分析
预测精度是衡量一个预测模型能否进行精准预测成绩走势的重要指标,是体现模型预测效力的关键,也直接决定了该模型的实际意义和应用价值。现利用灰色模型对第29、30届奥运会及第12~14届田径世锦赛男子200m冠军成绩进行预测,并对GM(1,N)模型和GM(1,1)模型的预测精度进行检验。
3.1 奥运会成绩预测
取表1中1-4周期内的A1数据和1-5周期内的A2数据建立||为0.31的GM(1,2)预测模型对第29届奥运会200m冠军成绩进行预测。根据式(1)-(13)得为0.9856,根据式(2)对进行还原后得预测成绩为19.72s;以表1中1-4周期内的数据建立GM(1,1)预测模型,根据白化响应式可得预测成绩为20.20s。
同理可得,以1-5周期内的A1数据和1-6周期内的A2数据建立||为0.51的GM(1,2)模型,预测成绩为19.25s;以1-5周期内的数据建立的GM(1,1)预测成绩为19.54s。表6所示为两模型的预测结果。
经对比后可知,GM(1,2)模型在第29届奥运会的成绩预测精度为97.81%,大于GM(1,1)的95.32%;其在第30届奥运会的预测精度为99.63%,也大于GM(1,1)的98.88%,说明GM(1,2)模型预测精度更高。
GM(1,2)模型之所以预测精度大于GM(1,1)模型,其原因在于GM(1,2)模型预测的实质是先计算获得行为变量和因子变量之间的关联系数,通过关联系数缩小误差,再在关联系数及两个变量走势的基础上进行数据建模,从而得出预测结果的。世锦赛与奥运会有着直接且重要的联系,且比赛成绩直接决定了该周期内运动员整体竞技水平的高低。因此以通过分析世锦赛与奥运会之间联系而建立的GM(1,N)模型比单纯分析往届成绩走势的GM(1,1)模型预测精度更高。
3.2 田径世锦赛成绩预测
若以表1中世界田径锦标赛200m成绩A2作为行为变量1,以奥运会成绩A1及世锦赛成绩A3作为因子变量2和3,可建立第12及14届世锦赛的灰色模型;若以A3作为行为变量1,A1及A2作为因子变量,则可建立第13届世锦赛模型。
分别取1-4周期内的1数据和1-5周期内的2数据建立第12届世锦赛GM(1,2)预测模型并以1-4周期内的1数据建立其GM(1,1)预测模型。同理,可建立预测第13、14届世锦赛成绩的GM(1,2)和GM(1,1)模型。其预测结果如表7所示。
由表7可知,利用GM(1,2)和GM(1,1)模型预测的第12届田径世锦赛男子200m冠军成绩精度分别为99.22%和95.78%;预测的第13届世锦赛的精度为99.90%和97.69%;第14届的精度为98.80%和97.68%。比较后发现GM(1,2)预测结果其精度均优于GM(1,1)模型,这再一次验证了GM(1,2)的预测精度高于GM(1,1)模型的观点。
为进一步检验GM(1,N)模型的预测精度,以A2作为行为变量,取1~4周期内的1数据、1-5周期内的2和3数据,根据式(1)~(16)建立拟合精度更高的GM(1,3)模型预测第12届世锦赛成绩,同理建立第13及14届世锦赛GM(1,3)模型。其预测的第12~14届田径世锦赛男子200m冠军成绩分别为19.52s、19.53s和19.41s,预测精度为98.28%、99.31%和98.75%。图5所示为第12~14届世锦赛中GM(1,1)模型与GM(1,2)和GM(1,3)模型预测精度的对比结果。
由图5可知,GM(1,N)模型的预测精度在整体上大于GM(1,1)模型,所得结果与奥运会预测结果一致。但由于系统中存在随机误差且干扰随机变量N值的提升而增大,经推演后发现拟合精度更高的GM(1,3)模型预测精度并不一定高于GM(1,2)模型,本例中更适宜采用GM(1,2)模型进行预测。因此在使用GM(1,N)模型的实际中,为达最优预测效果,应在模拟推演的基础上选择合适变量数值进行建模。
4 结论
(1)GM(1,N)模型可根据预测运动项目的不同设立不同类别的因子变量,数据获取范围及可用程度获得提高。
(2)通过计算证明,GM(1,N)预测模型的拟合精度和预测精度均大于GM(1,1)模型,可较好模拟真实成绩走势,更适宜进行成绩预测。
(3)在GM(1,N)模型中,随着变量N值增加,模型函数与原始成绩的拟合精度不断增高,增长幅度逐步减小。当N取极大值时,模型固有误差可达无穷小量。
(4)由于系统中存在随机误差使拟合精度受到干扰。在使用GM(1,N)模型时,应通过模拟推演确定变量N值进行建模。
参考文献
[1] 娄光大.略论灰色控制系统理论在体育中的应用[J].体育与科学,1986,6(4):10-14.
[2] 范振国.田径运动训练中的灰色系统模型控制[J].天津体育学院学报,2006(6):540-542.
[3] 詹金添.2008年世界与中国田径成绩比较的灰色预测[J].吉林体育学院学报,2007,23(1):11-13.
[4] 涂春景,杜和平,王玮.基于多维灰色GM(1,1)模型的奥运会中外女子游泳成绩预测研究[J].井冈山大学学报,2011,32(2):92-95.
[5] 刘嘉津.體育复杂系统的灰色预测方法探析[J].中国体育科技,2007(1):113-115.
