异重流潜入现象探讨Ⅱ：浑水水槽实验与分析

范家骅，祁 伟，戴 清

（中国水利水电科学研究院，北京 100048）

上一篇回顾了异重流潜入现象研究中前人的水槽实验情况与各家理论分析成果［1］，本篇分析异重流潜入现象在天然工程环境中和实验室水槽实验中所观测的成果，并利用水力学能量方程和动量方程，分析水库进口和引航道口门处异重流潜入点上下游断面的水沙因子关系；另外还将前人理论研究结果略作推演后与本文理论分析公式相比较；最后对结论和异重流研究中若干问题进行讨论，并对今后需要开展的研究工作提出了自己的看法。

1 水库中浑水异重流潜入点的观测

河流浑水水流进入水库壅水区，在浑水异重流潜入点附近可观察到清浑水明显的分界线，水舌潜入时伴随着水舌下游出现的向上泛起的浑水旋涡，以及潜入点下游和两侧存在于表面的回流，并积集着漂浮物。

随着浑水在潜入过程中泥沙的落淤，潜入点的底部高程上抬；潜入点水深变浅时，潜入点的位置将向下游推进；当流量增加时，潜入点的位置也会向下游移动。潜入的浑水如负浮射流潜入库底，并向下游扩展运动。

天然水库中进行潜入点的水流流速和含沙量分布的观测比较困难（潜入点水面流速与含沙量值均为零）。这是由于水流随洪峰迅速改变，不易测量到正位于潜入点的流速和含沙量的垂线分布。官厅水库、三门峡水库的几次较典型的潜入点流速和含沙量分布，参见文献［2］。

2 浑水实验

2.1 浑水异重流潜入点实验 实验目的：在水槽内观测浑水进入壅水区沿纵向的流速和浑水浓度的变化。实验之初，首先将槽内充满清水，槽内首部段的槽底比降为0.03，槽宽0.15 m，直段总长20.6 m；然后接以90°的弯道和4.5 m的直段，最后与扩大段相联结。扩大段水深较深，使异重流流入扩大段前端跌坎后形成临界水深，以避免回水影响。进槽流量用体积法测定。进入槽内浑水首先与槽内清水相混，浑水在前进过程中与清水相遇，在一定地点潜入底部形成异重流。

实验中测量潜入点上游、潜入点及其下游各断面流速和含沙量分布。流速用旋浆流速仪测量，含沙量则虹吸出各点水样，采用烘干称重法得出。此外还通过玻璃窗记录沿程清浑水交界面高程；为了观察浑水潜入点处的水流泥沙特征，还专门进行潜入点的水力泥沙因子的测量。

实验中观察到：将一定泥沙含量的浑水引入水槽中，浑水将在一定水深处潜入，当改变清水水位时，潜入点位置也随之改变，但潜入水深并不改变。槽内清水水位增加时，潜入点位置上移；清水水位下降时，潜入点位置下移。当在一定的清水水位、浑水泥沙含量和底部比降等条件下，如将流量增大，则潜入点位置下移；将流量减小，则潜入点位置上移。

观测表明：在15 cm宽、槽底比降为0.03的水槽中，当浑水流量为300～3800 cm3/s、进口含沙量为3～19 kg/m3，泥沙d50粒径为0.002～0.003 mm范围内时，得到如式（1）的平均关系［3］，同时水槽实验数据与三门峡、官厅水库的实测资料点绘于图1中。

式中：Fp为潜入点处的密度Froude数；hp为潜入点水深；up为潜入点平均流速；g′=∆ρ/ρ，∆ρ为浑水与清水的密度差。

另外实验中观测浑水潜入点至异重流沿程各断面的流速分布，并计算单宽流量（异重流交界面至底部）的沿程变化。多次测量表明潜入点以及其下游异重流流量沿纵向减小（见图2）。图2中底部以上3 cm以内的流速未能观测，因旋浆流速仪的直径为3 cm，且临近底层流速过低难于观测。计算潜入点上游、潜入点及其下游各断面流量，可得潜入点流量约为进槽流量的0.9，下游异重流流量约为潜入点流量的0.9。

图2 异重流潜入实验流速分布沿程变化

图1 浑水潜入点up与 g′hp的关系

2.2 潜入点水槽实验观察到的现象 水槽实验中观测进口断面水深、潜入点水深以及潜入点下游稳定段的异重流水深。实验中进槽流量在进入壅水区的流态分为两种情况：（1）浑水进入壅水区时产生水跃，在潜入区浑水水深逐渐加大，至潜入点处水深为最大，此处浑水潜入槽底形成底部异重流，其后浑水水深逐渐变小，直至稳定段水深保持基本不变；（2）浑水进入壅水区时未产生水跃，进入壅水区时水深逐渐增大，直至潜入点处水深为最大，潜入后浑水水深逐渐变小，至异重流稳定段时水深基本保持不变。

比较两种进水流态，不论存在水跃或不存在水跃，浑水水流均在进入壅水区后水深沿程增加，流速沿程减小，势能与动能两者处在前者增加、后者递减的变化中，直至潜入点处浑水开始潜入，此时势能趋于减小、动能趋于增加，直至趋于稳定段时势能与动能两者之比基本保持不变，见图3。

图3 潜入点上下流态示意图

由此可见：实验的进槽流量、含沙量为一定时，浑水水流进入壅水区时会调整其水流的内部结构，至潜入点处潜入时并不因水流进口流态的不同而发生改变。点绘进口断面处的密度Froude数F0与潜入点Fp两者的关系如图4所示，由图中可见F0对Fp几乎没影响。Stefan和Johnson［4］点绘Akiyama和Stefan［5］用冷水进行的潜入点实验的F0和Fp关系，也同样说明两者无大关系。

图4 浑水潜入试验F0和Fp的关系

此前笔者进行根据异重流渐变流运动方程的水深变化分析，发现当交界面水面线延伸到潜入点之间，存在一水流临界点，因潜入点位于临界点上游，因此可以断定潜入点的密度Froude数Fp应小于临界密度Froude数Fc（=1）；而从浑水水槽实验资料得Fp=0.63～0.91，平均值为0.78（见图1）；还有在长50 m、宽0.5 m的水槽中进行浑水潜入点实验得到Fp=0.62。

此外还观察到潜入点下游潜入区的交界面水面线的形状：自潜入点起交界面曲线呈微凸形与微凹形线的转折点位于潜入区的中间一半距离。实测各测次的潜入区长度大部分在300～400 cm之间，潜入点水深在5～17 cm之间，异重流水深在3～12 cm之间。

以上异重流潜入点Fp实验成果发表后，陆续有专著［6-8］、设计手册［9-10］、论文以及研究报告引用以上公式，并用于各水库异重流潜入点的实际分析中，同时还扩展运用于其它的工程之中；若干异重流潜入点实验研究者发表论文多引用本文作者Fp实验成果（如曹如轩［11］、焦恩泽［12］等），还有的对潜入点进行分析并修正Fp表达式［13-15］，也有的在综合讨论水库淤积问题中予以引用［16-20］。

3 理论分析

图5 异重流潜入概化图

3.1 水库异重流潜入 分析潜入点现象可利用流体力学的能量方程和动量方程。这里拟根据实验中以及天然水库中所观察到的现象，考虑潜入区上下层水体的掺混来推求潜入点以及稳定段异重流的水流参数。

（1）利用动量方程进行分析计算。考虑试验中观察到潜入混合区内存在上下层水体的交换，即上层进入下层（正掺混）或下层进入上层（负掺混）的水量掺混，分析方法类似先前所作的异重流水跃的方法［21］。

概化图形参见图5，图中ρp、hp和up分别为潜入点处异重流的密度、水深和流速；、ρd、hd和ud分别为潜入点下游稳定区异重流的密度、水深和流速；ρ和ua为上层水流的密度和流速。设qE为上层进入下层的水量，有：qE=E(hpup)=Eqp，此处E为掺混比值。由异重流水量平衡方程得：

其中：且KQ＞1时为正掺混（上层水体进入下层水体）；KQ=1时为无掺混；KQ＜1时为负掺混（若干试验表明，盐水潜入实验和冷热水实验时KQ＞1；而浑水潜入实验时KQ＜1）。

异重流的密度通量与不可压缩的连续方程分别为：

当考虑掺混因素的动量方程为：

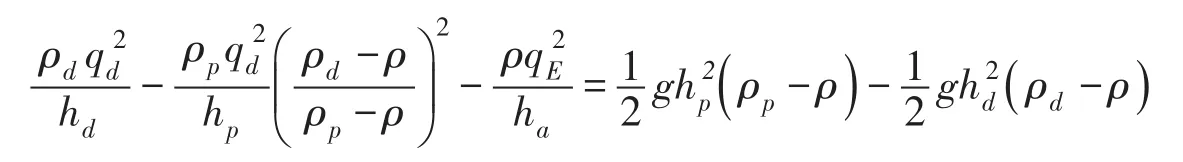
式中：ha=hp-hd。由于为小项，与其他多项比较可以忽略，故得：

式中ρp≈ρd，此假定即忽略了潜入点含沙量与其下游异重流含沙量的变化。因此近似地有下式：

式中：当忽略掺混即KQ=1时，则有

（2）利用能量方程分析。浑水异重流进入水库壅水区时，在一定水深处潜入库底形成异重流向前运动。按照von Karman［22］分析方法，写出交界面上A和B两点的Bernoulli方程（图6），则得：

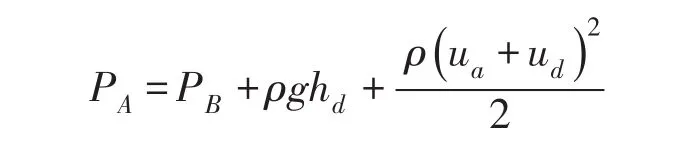
图6 水库异重流潜入概化图

式中：PA和PB为A、B两点上的压力，ua为上层流流速。由于水流潜入时形成的初始异重流流动为非恒定流，流速为ud，今叠加一个向上游的流速u=-ud，可使流动变为恒定运动，有：

以上两式相减，得：

观察水库异重流潜入点附近，浑水水流潜入时导致水库水面出现回流，并伴随有漂浮物，浑水水流在水库之中潜入，带动部分水库水体，流速大时还会捲吸部分水量进入异重流（正掺混）；但同时异重流在运动过程中，泥沙会沿程减少，导致异重流部分水量也会进入水库水体之中（负掺混）。浑水水槽实验中曾观测到潜入点流量略大于异重流流量，存在负掺混现象。现忽略此负掺混，设水库中上层水流流速ua=0，并设可得：

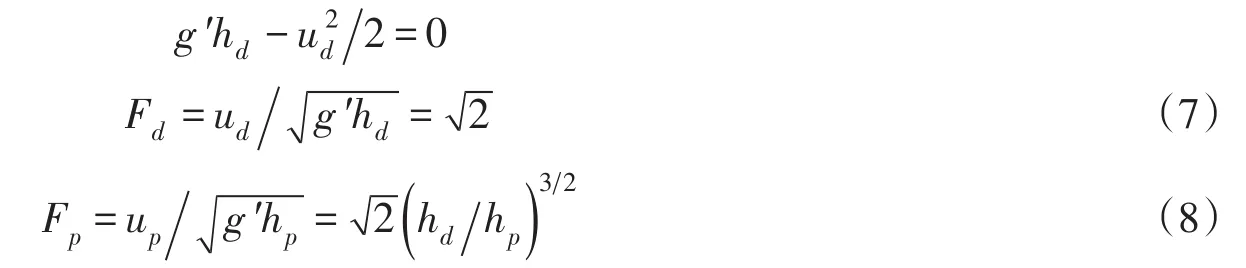
式（7）中Fd为潜入点下游异重流稳定段的密度Froude数；式（8）为潜入点的密度Froude数与稳定段异重流水深同潜入点水深之比值hd/hp的关系式。

另一种用能量方程求解方法是根据概化图形图5，第一断面为潜入点断面，第二断面为潜入区下游稳定异重流断面，忽略能量损失并忽略水量掺混，可写出下式：

与连续方程uphp=udhd联解，令得：

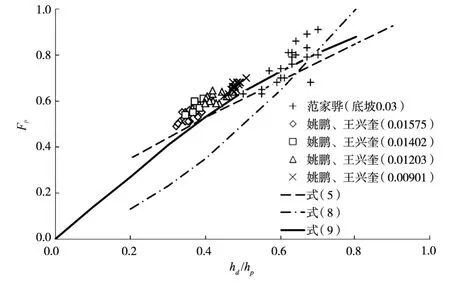
图7 水库浑水异重流潜入点实验

图7中点绘本文作者以及姚鹏和王兴奎［23-24］浑水异重流潜入点水槽实验的潜入点Fp和hd/hp各实测点，还有本文理论分析（动量方程和能量方程）两条关系线式（5）与式（9）。从图中可见实测数据与理论分析计算值两者较接近，但第三条线式（8）偏差较大。

3.2 船闸交换水流的异重流潜入 上节是浑水进入水库壅水区潜入形成异重流的情况，本节要讨论的是船闸交换水流的潜入情况，或者是在河渠或与支流交叉处河道浑水潜入支流的情况。

前人进行盐水实验时，在水槽内用隔板隔开，一边盛盐水，另一边盛清水，水位相同。当隔板抽去后，可见盐水下层以某种初速向前运动，而上层清水向反方向运动，且下层盐水层的流速因槽壁、槽底以及交界的阻力小于上层清水层流速。我们进行的浑水实验，布置河道浑水水流与引航道成某种角度，引航道内灌满清水，也采用隔板隔开。当抽去隔板后，河道浑水潜入引航道形成异重流，而引航道内的清水则在上层向反方向运动，流至河渠交界处，并流出渠口进入河道。

（1）利用能量方程分析。根据上述流态以及实验观测到上下层水流运动速度比较接近的情况，可设式（6）中ua=ud，故可得：

利用流量连续方程，可得：

式（11）是在忽略浑水从河道潜入引航道时两层水流之间的掺混，以及忽略能量损失等条件下，根据能量平衡方程获得的潜入点Fp与hd/hp比值的关系式。有一点需要说明，上式中的up值，是用连续方程求得的计算值，并非实验中的实测值。（本文水库壅水区潜入点实验中up为实验值。）

本文上一篇［1］的表4中列出了许多学者进行盐水交换水流的实验结果［1］，以及有学者如O’Brien［25］用能量方程、Abraham［26］以及Yih（易家训）［27］运用能量方程进行了理论分析工作，得同一公式，如下：

利用水流连续方程，可得：

以上用能量方程分析得引航道口门潜入点还引用各家理论分析（能量方程或动量方程）得Fp=k/2。

（2）利用动量方程分析。按照图6所示交换水流的概化图，用动量方程来分析引航道口门浑水潜入开始形成异重流时刻的异重流前锋流速和潜入点处的Fp值。即在实验中插板两边分注浑（盐）水和清水，当提起插板后，上层清水会向出口方向运动，下层浑水会向引航道内运动。我们重点关注当插板提起后很短时间内的异重流前锋流速及其水深等值。

为使运动为恒定，在右边叠加一个等于异重流流速ud的流速；其次忽略两层水体之间的掺混，可写出潜入点断面与异重流前锋断面之间的动量方程：

式中：

连续方程为：

可导得：

上式与实际资料所得的k=0.6～0.3，Fp=0.3～0.1相吻合。如对上式中略去小项k2，则上式变为Fp=k2。

点绘的运河平交穿黄（河）浑水实验的相关图见图8；图中还点绘Kersey和Hsü［28］的盐水交换水流实验的的实测数据，他们用3种不同的底坡（平底、正坡和负坡）进行实验；图中还点绘本文所导得的（自能量方程）、（自动量方程）以及Fp=k2的关系线，可见在k＜0.6实测资料范围内，理论线与实测值较为符合。

为了清晰地了解分析结果，将上述结果列于表1中，以便对比。

图8 引航道异重流潜入点浑水和盐水实验

表1 异重流潜入实验与理论分析结果

3.3 本文浑水异重流潜入点理论公式与前人理论公式的对比 根据本文浑水潜入点实验结果以及进行理论分析求得的表达式，有必要对前人潜入点水流理论分析的各种表达式进行分析对比，以判断是否符合水槽浑水潜入点实验结果。因此本节将对各家研究结果逐一作推演和比较。

von Karman［22］的研究中得到浑水潜入点的关系式：

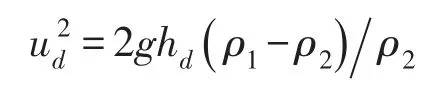
如用于水库异重流潜入时，可设总水深为hp，令uphp=udhd=q，设可得：

此式与浑水实验数据偏差较大。

Benjamin［29］的研究工作，应用于异重流则有［1］：

当k=0.5时Fp=0.5。在k=0.3～0.6之间时，此式与浑水实验点据比较，实验数据Fp值偏大0.1～0.15。考虑到水槽实验受槽宽影响，实验测得的Fp值可能偏大，此点在分析对比时应予以注意。

Singh和Shah［30］导得：

可导得即KQ=1时（无掺混）的式（5）。

Savage［31］利用Bernoulli方程得：

从而导得

式（17）当k=0.5时Fp=0.5，其曲线与Benjamin公式的曲线基本相同。

Jain［32］用动量方程得：

Jain设可得：

Jain曾点绘Fp与（1-k）的关系线，指出Savage分析得k=0.5时Fp=0.5是上式的一个解。

当β=0时

当β=0.5时

同本文实验值比较，β=0的公式接近水库潜入点实验的实测点据。β=0.5的公式，k=0.5、Fp=0.5曲线与Benjamin公式曲线相同，其理论计算值较水槽实验值为小。因此β=0和β=0.5表示不考虑能量损失与考虑一定能量损失两种情况，似均可用于水库壅水区异重流潜入点Fp的估算。

Jain用能量方程得：

如令得：

当α=0，β=0时有：

此式与式（19）很接近。

当α=0，β=0.5时可得式（17）：

此式k=0.5时Fp=0.5，其曲线与Savage公式相同。式（22）和式（17）同式（19）和式（20）一样，可用于水库壅水区异重流潜入点Fp的计算。

另外还有其他学者所求得的Fp表达式可推导得同一公式Egashira和Ashida［33］推导得Fd表达式：朱鹏程［34］和曹如轩［35］分别推导得：姚鹏［24］论文中得到以及姚鹏推得：以上4式均可推导得到KQ=1时的式（5）。

方春明等［36］用动量公式推导得他们还用能量方程得：

若令∆E=0，∆h=0，可得与Jain相同的结果式（22）：

Akiyama和Stefan［37-38］与Parker［39］用他们的潜入点CVI动量方程，可导得不同方程。Akiyama文中式（16）：

式中混合系数：

可得：

令γ=0，亦即令ua=0，可得：

Parker根据与Akiyama相同的图形推导CVI动量方程，导得：

当γ=0，亦即ua=0，表示水库上层水流速度为零，则有

当γ=1，即ua=ud，表示引航道口门下游的水流情况，则有：

Parker的γ=0和γ=1理论线与本文水库潜入点和引航道口门潜入点两类实验实测数据均接近。

此外，根据Parker文中式（28）所导得Fd在γ=0时：

则有：与连续方程联解可得：

Fp=k与两式曲线较接近，而更接近于水槽实验的实测值。

表2分类列出了水库异重流潜入点和引航道口门潜入点两大类，两类中又分应用能量方程或动量方程两种分析方法，共导得4类Fp公式，如图9—图11所示。表2中，除去水库壅水区潜入点关系式与实验数据相差较大外（未点绘在图9上），所列公式均基本符合两种水槽实验数据。从表2比较中可看出：

（1）表2中异重流在水库壅水区潜入，应用能量方程情况下，Benjamin的Savage的和方春明等的（令∆E=0，∆h=0）同 本 文 研 究 的相比较，前两公式与本文研究接近，后一公式与本文研究相同。

（2）表2中异重流在水库壅水区潜入，应用动量方程情况下，Jain的与本文理论分析接近。Singh和Shah、Egashira和Ashida、朱鹏程、曹如轩、方春明、Akiyama和Stefan、Parker和Toniolo的均与本文理论分析结果相同。

（3）表2中异重流在引航道口门潜入，本文理论研究利用动量方程、能量方程得和O’Brien、von Karman、Abraham的与本文研究公式相同，Parker的与本文公式中在实验资料范围内接近。

表2 本文分析研究与各家表达式推导所得公式的对比

图9 水库异重流潜入理论分析（能量方程）

图10 水库异重流潜入理论分析（动量方程）

图11 引航道口门潜入点理论分析Fp表达式

4 结论与讨论

4.1 异重流潜入点Fp的研究

（1）水库中现场观测和浑水水槽实验得到Fp=0.5～0.8；盐水、冷热水实验得到Fp=0.3～0.8，或用参数hp表示为：引航道口门浑水潜入Fp在0.1～0.3范围内变化；见文献［1］表1～表3。k-ε数学模型和水沙模型的数值计算亦显示计算值Fp与实验值Fp接近。

（2）有学者利用水力计算方法求取Fp值，其中Fp为底坡、阻力（底部和交界面）、掺混系数等因子的函数，虽得出不同关系式，但未能获得可供计算的公式，笔者在简化条件（无掺混、不考虑阻力的影响条件下）后求得Fp和hp，并与实验资料进行了比较。如Savage和Akiyama等所推导的hp关系式同Singh的盐水潜入点实验资料进行了比较，见文献［1］的表2和表3。

（3）本文研究利用能量方程和动量方程分析水库壅水区以及引航道口门的浑水异重流潜入点Fp和hdhp的关系式，并将各家研究的不同形式表达式作进一步推导得表达式，经过同本文研究所得公式进行对比，可见除去之外，各家公式与本文公式有的相同，有的是形式不同但均与本文浑水实验结果相符，见表2。

4.2 有关掺混（混合）系数物理意义的讨论 Akiyama和Parker在分析中虽定义一混合系数其物理意义是上层流体单宽流量与潜入点断面单宽流量的比值，但并不意味着两层水体的混合。笔者认为γ代表上层水体流量与下层异重流流量的比值，当上层水体无流量（如水库中异重流潜入的流态），分析中可假定上层清水层ua很小可忽略不计，即假定γ=0；当上层流量与下层流量相同（如引航道口门异重流潜入的情况）时γ=1。笔者根据上述理解将Akiyama和Parker分析结果中令γ=0、γ=0.5用于推导水库壅水区异重流潜入点Fp=f()k的表达式；令γ=1用于推导引航道口门异重流潜入的Fp表达式。关于掺混，它应为上下层流体在交界面相对运动产生剪力并引起两层水体的交换。从这个意义上讲利用γ来表示混合可以理解。但掺混现象在浑水异重流的实验中，不仅是上下两层在交界面上剪力引起两层之间水量的交换，同时存在由于异重流含沙量的变化、泥沙沉淀导致异重流有清水进入上层水体的另一种掺混。对于水槽浑水异重流运动中交界面水体掺混系数，笔者曾分析实验资料得到在缓坡时掺混系数为负值、在陡坡时为正值的结论［40］。

笔者曾在潜入点实验中用旋桨流速仪沿纵向施测异重流垂向流速分布，并计算各断面交界面以下的单宽流量，发现单宽流量沿程减小；其次现场实测引航道潜入点至异重流沿程流量也减小。但是俞维升的浑水异重流实验中［41］，测量各断面流速分布、自底部至流速为零的水平线之间的流量，沿程显示流量增加（有个别流量减小，未采用）。

笔者认为异重流交界面的流速并不等于零而是有一定值，因此俞维升的流量测量应计算底部以上至交界面，而不是至流速为零的点之间的流量。笔者在推导潜入点Fp表达式引进KQ掺混系数，未能作KQ对Fp的影响的计算［42］。这是由于各家实验结果不同（盐水或冷热水实验与俞维升浑水实验相同结果），加之我们以前所用的旋桨式流速仪不能测3 cm/s以下的流速，姚鹏所用测速仪可能精度较高，但未见流速分布数据发表，故掺混系数问题有待今后继续研究。

4.3 水流模型数值计算 利用水流模型数值计算，可获得水流进入水库壅水区流速随水深增加、流速逐渐降低至潜入点处流速平均为最小、水面处流速为零、潜入区流速逐渐加大直至异重流流速基本保持不变，能清晰地显示水流改变的连续过程。

Farrell和Stefan、Bourner等利用k-ε模型（温度方程）、方春明等利用水流垂向二维模型（悬沙方程）计算潜入水流；Farrell和Bourner等计算的潜入点水深较实验值大20%，而方春明等的计算潜入点Fp与曹如轩实验值基本符合。

方春明等、Farrell等和Bourner等计算水流流速垂线分布的沿程变化和密度（浑水、冷水）垂线分布的沿程变化，可了解到沿程流速和密度的二维分布情况，以及水流从上游至潜入点乃至沿库底形成异重流的过程。水流紊动二维模型数值计算相比一维水力计算，可得到潜入点断面水面和底部流速为零及水面含沙量为零的判别细节，但在数值计算中须选取符合实际的紊流和泥沙运动的参数值。

4.4 今后工作管见

（1）浑水与盐水潜入点水槽实验的各值，在工程设计中可预估水库壅水区潜入点大致位置。对于引航道淤积量的估算，因异重流潜入点在口门处附近，故有了Fp中各水力泥沙因子各值即可计算一定时间内的引航道内淤积量，能满足设计要求；其次水槽浑水实验所得的潜入点Fp值受到槽宽的影响，还需要进行分析研究。

（2）虽然已有数学模型计算了从进口至潜入点乃至底部异重流沿程的水流流速分布和含盐（沙）量分布，但仍需要得到浑水水槽实测资料的验证，希望以后能看到这方面的二维数模研究工作。另外为了研究水库壅水区异重流潜入与异重流沿程悬沙淤积（或冲刷），有必要在数学模型中包含泥沙冲淤方程以计算明渠段以及潜入段下游异重流含沙量分布的沿程变化，此种模型可应用于计算水库淤积分布和淤积量，还可应用于引航道、引潮沟或河口入海段航道的盐水和泥水入侵长度及泥沙沿程淤积分布的计算（即盐水楔和浑水楔长度及楔长沿程泥沙淤积的计算）。

［1］范家骅，祁伟，戴清.异重流潜入现象探讨Ⅰ：水槽实验与理论分析成果回顾［J］.水利学报，2018，49（4）：404-418.

［2］FAN Jiahua.Density currents in reservoirs［C］//Workshop on Management of Reservoir Sedimentation.New Del⁃hi，1991.

［3］范家骅，等.异重流运动的实验研究［J］.水利学报，1959（5）：30-48.

［4］STEFAN H，JOHNSON T.Negative buoyant flow in diverging channel.Ⅲ .Onset of underflow［J］.Journal of Hydraulic Engineering，1989，115（4）：423-436.

［5］AKIYAMA J，STEFAN H.Onset of underflow in slightly diverging channels［J］.Journal of Hydraulic Engineer⁃ing-Asce，1987，113（7）：825-844.

［6］钱宁，万兆惠.泥沙运动力学［M］.北京：科学出版社，1983.

［7］张瑞瑾.河流泥沙动力学［M］.北京：中国水利水电出版社，1998.

［8］韩其为.水库淤积［M］.北京：科学出版社，2003.

［9］水利部水利水电规划设计总院.水工设计手册（第2版）第2卷：规划、水文、地质［M］.北京：中国水利水电出版社，2014.

［10］涂启华，扬赉斐.泥沙设计手册［M］.北京：中国水利水电出版社，2006.

［11］曹如轩.高含沙异重流的实验研究［J］.水利学报，1983（2）：49-57.

［12］侯素珍，焦恩泽.小浪底水库异重流有关问题分析［J］.水利学报，2003（6）：11-14.

［13］李涛，夏军强，张俊华，等.水库异重流潜入点流速分布及其判别式改进［J］.工程科学与技术，2017，49（2）：62-68.

［14］李涛，张俊华，马怀宝，等.异重流潜入重力修正系数研究［J］.人民黄河，2012，34（7）：28-29.

［15］赵琴，李嘉.浑水异重流潜入理论模型及影响因素研究［J］.泥沙研究，2012（1）：58-62.

［16］李书霞，夏军强，张俊华，等.水库浑水异重流潜入点判别条件［J］.水科学进展，2012，23（3）：363-368.

［17］朱素会，耿胜安，王德军.小浪底水库异重流潜入点区特性分析［J］.华北水利水电学院学报，2011，32（2）：23-25.

［18］解河海，张金良，王少波.水库异重流潜入点深度预测模型［J］.中国农村水利水电，2010（5）：61-64.

［19］高亚军，陆永军，李国斌.黄河小浪底库区高含沙异重流的运动过程分析［J］.水利水运工程学报，2008（2）：60-66.

［20］李涛，谈广鸣，张俊华，等.水库异重流研究进展［J］.中国农村水利水电，2006（9）：21-24.

［21］范家骅.伴有局部掺混的异重流水跃［J］.水利学报，2005，36（2）：135-140.

［22］von KARMAN T.The engineer grapples with non-linear problems［J］.Bull.Am.Math.Soc.，1940（46）：615-683.

［23］姚鹏，王兴奎.异重流潜入规律研究［J］.水利学报，1996（8）：77-83.

［24］姚鹏.异重流运动的试验研究［D］.北京：清华大学，1994.

［25］O'BRIEN M P，CHERNO J.Model law for motion of salt water through fresh［J］.Trans.ASCE，1934（99）：576-594.

［26］ABRAHAM G.Reference Notes on Density Currents and Transport Processes［R］.Delft，1975.

［27］YIH C S.A study of the characteristics of gravity waves at a liquid surface［D］.Iowa：State Univ.of Iowa，1947.

［28］KERSEY D G，HSÜ K.Energy relations of density current flows：an experimental investigation［J］.Sedimentolo⁃gy，1976（23）：761-789.

［29］BENJAMIN T B.Gravity current and related phenoma［J］.J.Fluid Mech.1968（31）：209-248.

［30］SINGH B，SHAH C R.Plunging phenomenon of density currents in reservoirs［J］.La Houille Blanche，1971，1（26）：59-64.

［31］SAVAGE S B，BRIMBERG J.Analysis of plunging phenomena in water reservoirs［J］.J.Hydraul.Res.，1975，13（2）：187-205.

［32］JAIN S C.Plunging phenomena in reservoirs［C］//Proc.Symp.On Surface Water Impoundments，Minnesota：Minneapolis，1981.

［33］EGASHIRA S，ASHIDA K.Condition that suspended load plunges to form gravity current［C］//19th Proc.of the Conference on Natural Disaster Science.Japan：1978.

［34］朱鹏程.异重流的形成与衰减［J］.水利学报，1981（5）：52-59.

［35］曹如轩，任晓枫，卢文新.高含沙异重流的形成与持续条件分析［J］.泥沙研究，1984（2）：1-10.

［36］方春明，韩其为，何明民.异重流潜入条件分析及立面二维数值模拟［J］.泥沙研究，1997（4）：68-75.

［37］AKIYAMA J，STEFAN H.Theory of plunging flow into a reservoir：Internal memoratum［R］.St.Anthony Falls Hydraulic Lab.，Univ.of Minnesota，1981.

［38］AKIYAMA J，STEFAN H.Plunging flow into a reservoir：theory［J］.J.Hydraul.Eng.，1984，110（4）：484-499.

［39］PARKER G，TONIOLO H.Note on the analysis of plunging of density flows［J］.Journal of Hydraulic Engineer⁃ing，2007，133（6）：690-694.

［40］范家骅.浑水异重流水量掺混系数的研究［J］.水利学报，2011，42（1）：19-26.

［41］俞维升.水库沉滓运动特性之研究［D］.台北：台湾大学，1991.

［42］范家骅.异重流交界面波动失稳条件［J］.水利学报，2010，41（7）：849-855.