随机粗糙面上解决低频崩溃问题的电磁散射研究

高正平，郭靖锋

（电子科技大学微电子与固体电子学院 四川 成都 610054）

1 引言

随机粗糙面的电磁散射研究，一直以来都是材料学、电磁学等各个领域研究的重点关注课题[1-4]。特别是在最近几十年来，各种算法在随机粗糙面的RCS研究上取得了巨大的进展，本文重点解决的是计算随机粗糙面的电磁散射系数时，传统的积分方程产生的低频崩溃问题。矩量法（MOM）是求解电积分方程的最常用一种方法。本文先用商业FEKO软件中矩量法MOM对随机粗糙面双站散射系数σ进行计算，然后再用自编程软件的中AEFIE算法来解决计算随机粗糙面的RCS时，传统电场积分方程面临的低频崩溃问题。并用自编程软件计算得出随机粗糙面的散射系数，通过与商业FEKO软件中传统的多层快速多极子算法（MLFMA）算法计算的数据进行对比，来表明新型积分方程的计算时间短，占用内存少等优势。

MATLAB软件是当前制作数值3D模型最为流行的软件之一，本文用线性滤波法把随机粗糙面仿真出二维模型，再把二维模型导入到商业FEKO软件或自编程软件中去。为了提高自编程软件和用户之间信息交互能力，可采用可视化的用户接口即UI（User Interface）界面。本文利用Microsoft Visual C++ 6.0编程平台使用C++语言进行编程，用自编程的增量积分方程来计算随机粗糙面的电磁散射系数。

2 模型建立与算法的实现

2.1 计算机的硬件与软件配置

计算机中央处理器（CPU）采用的是Intel Core i7-6700HQ 2.6GHz，计算机内存（Memory）采用的是16GB（联想 DDR3 2400MHz），操作系统（OS）采用的是Windows 10 SP1（64位），开发平台采用的是Microsoft Visual C++ 6.0，开发语言使用C++语言。

2.2 二维随机粗糙面模型的建立

我们可以通过MATLAB等软件把高低起伏的地面仿真出二维随机粗糙面模型，随机粗糙表面由均方根长度δ和表面相关长度l两个基本参量决定[5-7]。

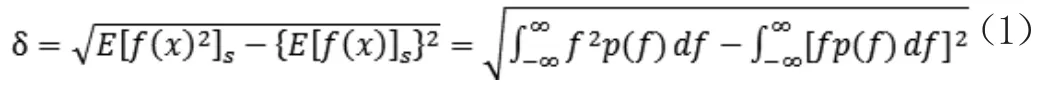
E[ ]表示整个随机粗糙面平均值，z=f（x）表示的是随机粗糙面高度起伏的函数表达式，高度起伏的分布情况则是由概率密度函数p（f）来表征。

对于一个随机粗糙表面，它的粗糙面特性并不仅用均方根来描述，另外的一个重要参数就是相关函数[8-9]。

将自相关函数进行归一化处理得到相关系数为

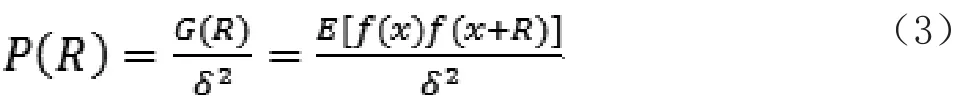
本文用蒙特卡罗方法（线性滤波法）生成一个二维的随机粗糙面，粗糙面上每一点的高度可表示为[10]

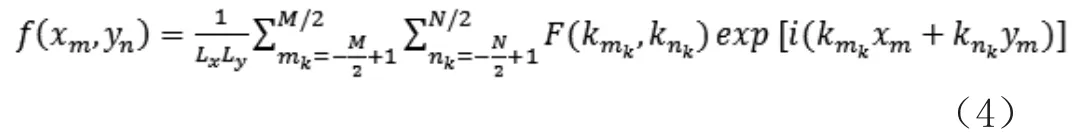
其中

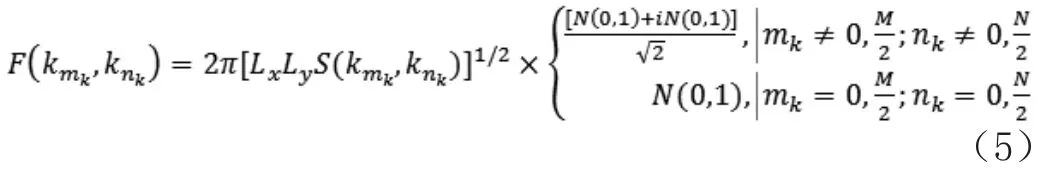
上式中表示要生成随机粗糙面的功率谱密度函数为[11]

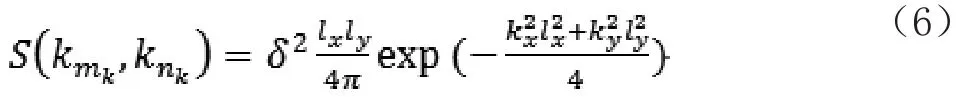
图1（a）、（b）、（c）和（d）是当均方根高度δ取值为0.05λ、0.1λ、0.2λ、0.3λ，相关长度l取固定值为0.5λ时的随机粗糙面图形

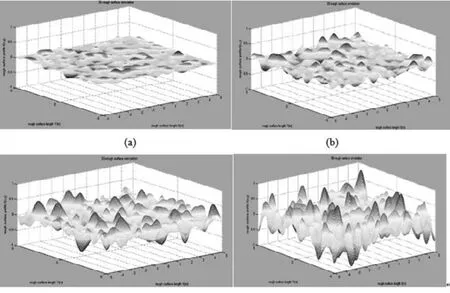
图1 随机粗糙面l=0.5λ：（a）δ=0.05λ；（b）δ=0.1λ；（c）δ=0.2λ；（d）δ=0.3λFig.1 random rough surfacel=0.5λ of （a）δ=0.05λ；（b）δ=0.1λ；（c）δ=0.2λ；（d）δ=0.3λ

图2（a）、（b）、（c）和（d）分别为当相关长度l分别取值为0.3λ，1λ均方根高度取固定值为0.1λ的二维粗糙面模型

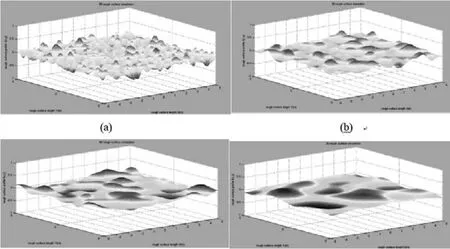
图2 随机粗糙面δ=0.1λ：（a）l=0.3λ；（b）l=0.7λ；（c）l=1λ；（d）l=2λFig.2random rough surface δ=0.1λ of （a）l=0.3λ；（b）l=0.7λ；（c）l=1λ；（d）l=2λ

从上述用MATALB软件仿真出来的二维随机粗糙面模型可以看出，在l固定的情况下，随着δ的增大，随机粗糙面的起伏也就越来越大，粗糙面的峰值和谷值的绝对值就越大。即粗糙面的高度起伏与均方根高度成正比。同样可以看出在δ为固定值时，l增大，随机粗糙面变化就变得缓慢。

2.3 增量型电场积分方程实现

增量型电场积分方程（AEFIE）是一种通过改变积分方程的形式来消除低频崩溃问题的一种有效方法，被提出后迅速成为有效的计算工具[12-14]。AEFIE中的矢量位和标量位被分离，电流连续性限制条件被用于建立额外的方程系统。通过采用合适的频率扩张因子，可以去除低频问题。

采用三角贴片对待求解的目标进行剖分。假定剖分后的三角贴片相关的内边有e条。RWG基函数为[15]

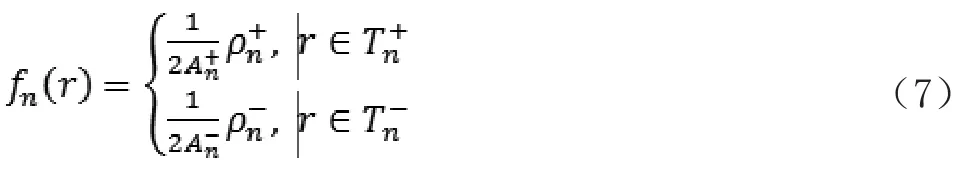
An+，An-分别为三角形Tn+，Tn-的面积。对于三角贴片，可以定义这样的脉冲基函数来表示电荷

通过这些基函数，可以定义三个矩阵V∈Ce×e，S ∈ Ce×e以及 P ∈ Ce×e

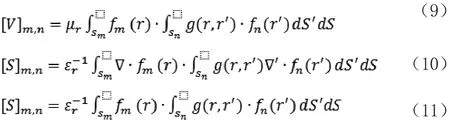
这样，传统的基于RWG基函数的 EFIE 可以写成[16]

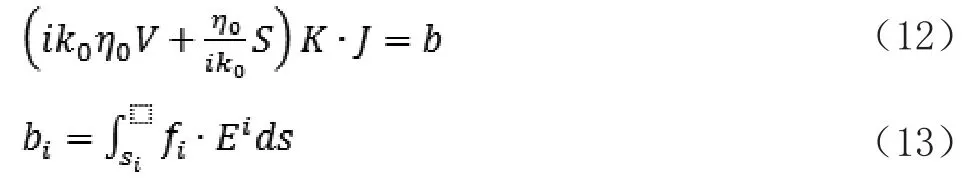
通过几何剖分模型中三角贴片和其公共边的关系构造一个连接矩阵∈Ce×e，其定义如下

标量位的矩阵表示

假定三角贴片上电荷密度的系数向量为d，那么d可以用下式表示

这样就可以得到源荷分离的电场积分表达式

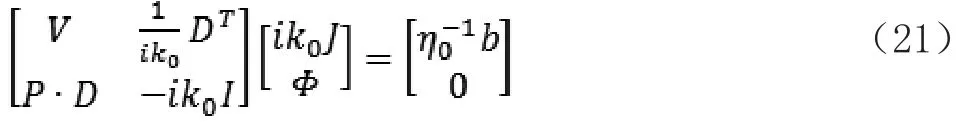
成功得到了增量型电场积分方程的实现方法，利用Microsoft Visual C++ 6.0编程平台使用C++语言对推导出的算法进行编程，软件程序主要由三个模块构成：（1）网格模型导入模块；（2）计算参数设置模块；（3）电磁计算程序模块。

3 计算结果及验证

本文采用波长为1米频率为f=300MHz的入射波，粗糙面长度L=10λ，入射角θi=30°。每个波长被剖分为30个单元。

垂直极化波入射时，取相关长度为固定值l=0.5λ，均方根δ取值为δ=0.05λ、δ=0.2λ。再取高度起伏均方根分为固定值δ=0.05λ，选取相关长度为分别为l=0.3λ、l=1λ。用商业FEKO软件中MOM算法计算随机粗糙面双站散射系数σ由于计算量过于巨大以及数值不稳定等原因导致FEKO内存不足，不能计算出电磁散射系数。再采用商业FEKO软件中MLFMA算法与自编程软件中AEFIE算法计算随机粗糙面双站散射系数σ，每种随机粗糙面取30个样本进行双站散射系数的计算并取平均值，最终得到计算时间与内存消耗量如表1，得到的RCS曲线图如图3、4。

表1 两种算法的计算时间与内存消耗Table.1 Chemical components of the prepared samples （mass fraction/%）

从上表可以看出无论计算时间还是对计算机的内存消耗AEFIE算法更具有一定的优势，与传统的MLFMA算法相比，AEFIE用MLFMA算法加速后消耗内存更少，计算用时更少。

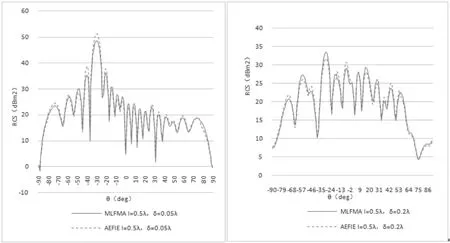
图3 均方根高度不同MLFMA和AEFIE算法RCSFig.3 RCS calculated by MLFMA and AEFIE algorithms with different root mean square heights

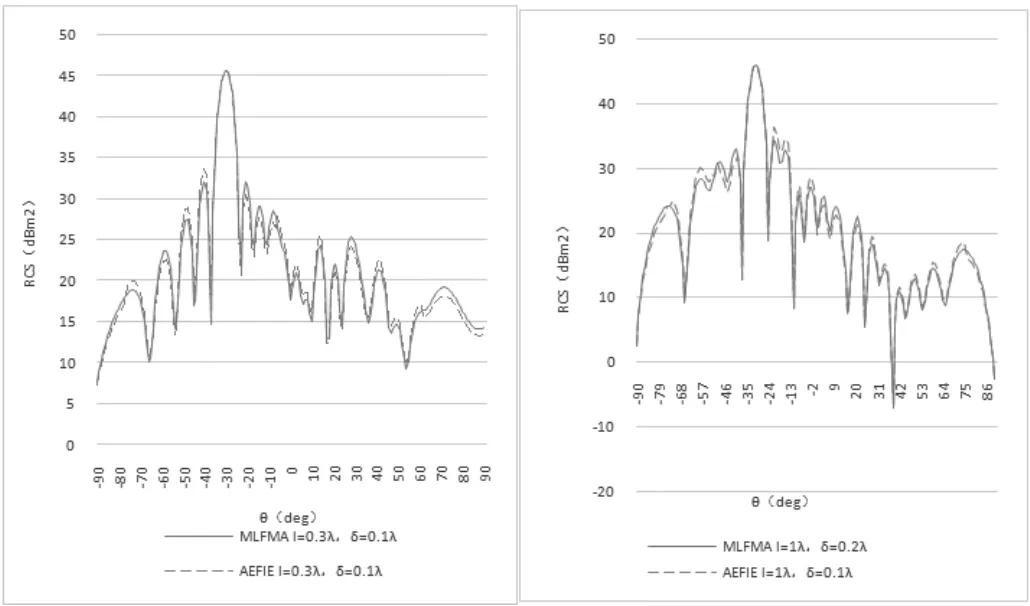
图4 相关长度不同MLFMA和AEFIE算法RCSFig.4 RCS calculated by MLFMA and AEFIE algorithms with different relevant length

如图（e）（f）所示，通过对照看出，商业FEKO软件计算随机粗糙面散射系数与自编程软件计算结果基本一致，表明了AEFIE方法计算随机粗糙面双站散射系数σ的准确有效性。同时通过图（e）验证了在镜向上，散射系数σ随高度起伏均方根δ的减小而增大，而在其余大部分的散射区域中，散射系数σ随高度起伏均方根δ的减小跟着减小。通过图（f）在镜向上，散射系数σ随高度起伏均方根δ的减小而增大，而在其余大部分的散射区域中，散射系数σ随高度起伏均方根δ的减小跟着减小。

4 结论

本文利用Microsoft Visual C++ 6.0编程平台使用C++语言进行编程，用自编程的增量积分方程的方法来求解低频TM波入射随机粗糙面导致传统积分方程出现低频崩溃问题。并用自编程软件的AEFIE算法与商业FEKO软件中MLFMA算法对随机粗糙面双站散射系数σ进行计算消耗的时间与内存的平均值，表明了AEFIE用MLFMA加速后与传统的MLFMA算法计算随机粗糙面散射系数σ的有占用计算机内存少，计算时间短等优势。同时通过得到的RCS曲线图，表明了AEFIE方法计算随机粗糙面双站散射系数 σ的准确有效性。同时验证了在镜像上，σ 随高度起伏均方根δ 的变小而增大，几乎不受l变化所影响，而在非镜像上，散射系数σ 随高度起伏均方根δ的减小跟着减小，却会随其相关长度l的减小而增大。

[1] D.R.Wilton and A.W.Glisson，O improving the electric field integral equation at low frequencies,URSI Radio Science Meeting Digest，Los Angeles,CA，June 1981，pp.24

[2] 逯贵祯，王宝发.高斯随机粗糙表面的电磁散射研究[J].电子学报，2002，30（6）：907-908.

[3] Thorsos E.The validity of the Kirchhoff approximation for rough surface scattering using a Gaussian roughness spectrum [J].1/++7 J AcoustSoc Am，1988，83（1）: 78-91.

[4] Wang X，Wang C F，Gan Y B. Electromagnetic scattering from a circular target above or below rough surface [J].Progress inElectromagnetics Research，2003，40: 207-227.

[5] Kuga Y，Phu P.Experimental studies of millimeterwave scattering in discrete random media and from rough surfaces [J].Progress in Electromagnetics Research，1996，14:37-38.

[6] 闫沛文，童创明，姬伟杰.SM FSIA/CA G快速计算二维分形粗糙面的电磁散射特性 [J].系统工程与电子技术，2009，31（9）:2117-2120 .

[7] 田炜，任新成.一维指数型粗糙土壤表面电磁散射的矩量法研究[J].科学技术与工程，2011， 11（10）：2211-2214.

[8] 郭立新，王蕊，吴振森.随机粗糙面散射的基本理论与方法[M].北京：科学出版社，2009:1-60.

[9] Bass.Wave Scattering from Statistically Rough Surfaces[C]. Oxford: Pergamum，1979.

[10] A.Ishimaru，and J S.Chen. Scattering from very rough surfaces based on the modified second-order Kirchhoff approximation with angular and propagation shadowing [M].J.Acoust.Soc. Am，1990:1877-1883.

[11] Bruce N C.Multiple scatter of vector electromagnetic waves from rough metal surfaces with infinite slopes using theKirchhoff approximation[J].Waves in Random and Complex Media，2011，21（2）:362 － 377.

[12] W. Wu，A.W.Glisson and D.Kajfez.，A Comparison of Two Low-frequency Formulations for the Electric Field Integral Equation,Proceedings of the 10th Annual Review of Progress in Applied Computational Electromagnetics，Monterey，California，Vol.2，pp 484-491.

[13] J.S. Zhao，W.C.Chew，Integral equation solution of Maxwell's equations from zero frequency to zero frequency to microwave frequencies，IEEE Transactions on Antennas and Propagation，Oct.2000，Vol.48，No.10，pp.1635-1645.

[14] Z.G.Qian and W.C.Chew，An augmented electric field integral equation for low frequency electromagnetcs analysis，IEEE Antennas and Propagation International Symposium，San Diego，Jul.2008.

[15] Z.G.Qian and W.C.Chew，An augmented EFIE for high speed interconnect analysis，Microwave and OpticaTechnology Letters，Oct.2008，Vol.50，No.10，pp.2658-2662.

[16] M.Taskinen and P.Yla-Oijala，Current and charg integral equation formulation，IEEE Transactions on Antennas and Propagation，Jan.2006，Vol.54，No.1，pp.58-67.