220 kV变压器短路状态三维瞬态电磁场数值模拟研究
2018-06-11何明高李德波周杰联冯永新
何明高,李德波,周杰联,冯永新,陈 拓
(1.广东省粤电集团有限公司珠海发电厂,广东 珠海 519050;2.广东电科院能源技术有限责任公司,广州 510060)
0 引言
随着变压器容量和电力系统容量的增加,变压器发生短路事故的风险也在逐渐增大,突发短路故障导致绕组所受的电磁力不但威胁着变压器的安全运行,而且对电网的稳定性也会造成巨大影响。大型电力变压器在短路事故中,绕组瞬时所受到的电磁力幅值将达到额定运行时的几百倍甚至更大,其绕组损坏主要原因就是绕组在辐向力和轴向力的共同作用下绕组结构强度不足或支撑结构强度不足,进而导致绕组变形或者轴向或辐向失稳。因此,对大型变压器发生短路时绕组所受电磁力进行准确计算,可以评估变压器抗短路能力,从而采取有效措施以减少事故的发生[1-14]。
孙昕对一台110 kV变压器在突发短路后,断路器快速重合闸动作下变压器绕组受到冲击电流,研究分析了该电流冲击下的电磁场和绕组静态电磁力分布[15]。李帅采用了Magnet有限元计算软件,分析了10 kV级油浸式配电变压器发生短路事故时的漏磁场以及绕组受力,并给出了提高配电变压器抗短路能力的具体措施[16]。王伟采用矢量磁位法,对变压器突发短路时的二维瞬态电磁场进行计算,得到各个线饼单元的磁通密度(简称磁密)和应力分布,并对导线承受短路能力进行了计算分析[17]。以上的研究在分析时都把绕组当作静态元件,这些都属于静态分析计算。然而实际短路过程中,绕组在受到巨大的短路电磁力的作用下,绕组线饼结构位置会发生些许改变,严重时可能导致安匝不平衡,造成变压器内部漏磁场变化,从而影响绕组所受的短路电磁力,即实际短路发生时,变压器绕组受力是多场耦合问题[18-21],这方面还缺乏深入研究[22-23]。
文中以1台三相三绕组油浸式电力变压器为例,在Maxwell软件中建立了变压器单相短路的三维有限元计算模型,采用Maxwell软件的瞬态磁场求解器仿真了该变压器发生单相外部短路时铁心主磁通和漏磁场,得到了电磁场分布和电磁损耗情况。
1 数值模拟边界条件
1.1 变压器的主要参数和结构
数值模拟中采用型号为 SFPSZ7-150000/220的三相三绕组有载调压电力变压器,该变压器及其绕组的部分参数详见表1、表2。
1.2 变压器实体建模方法
为减小计算难度,提升计算效率,该模型舍弃了绝缘垫块、绝缘纸筒等对变压器电磁场影响较小的部件。图1为变压器整体仿真计算模型,该模型外部加了变压器箱壳,箱壳外部还加了各方向均为变压器箱壳长度1.1倍的真空区域,作为变压器电磁场仿真计算的求解域。
文中首次建立了如此精细的变压器实体模型,变压器绕组为饼式结构,考虑了饼间油道等。以往研究为了提高计算效率,通常都对变压器模型进行了极度简化,例如较多学者将变压器绕组模型简化为一个圆筒,但这样会产生较大误差。

表1 算例产品的主要技术参数
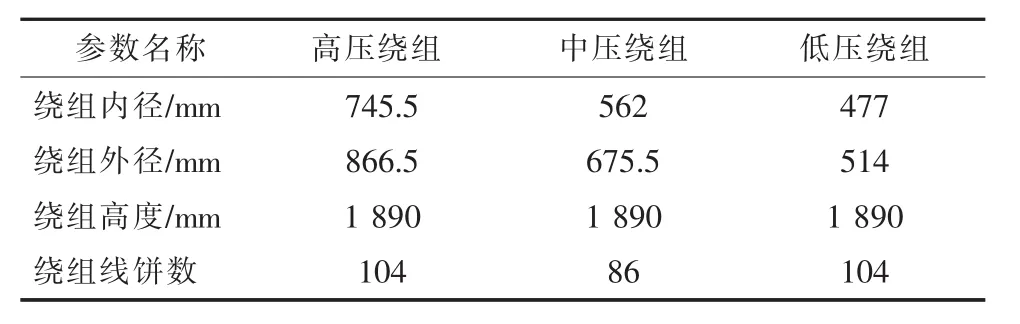
表2 产品的绕组参数

图1 变压器仿真模型
1.3 材料参数的选取
模型主要材料参数包括变压器绕组电导率、变压器铁心磁化曲线等。绕组电导率为0.021 35 s/m(75℃),拉板和夹件油箱壁等结构材料为Q235普通钢板,变压器铁心硅钢片型号为30ZH110。
1.4 激励设置
以A相高对中短路为例,其电路模型设置如图2所示。
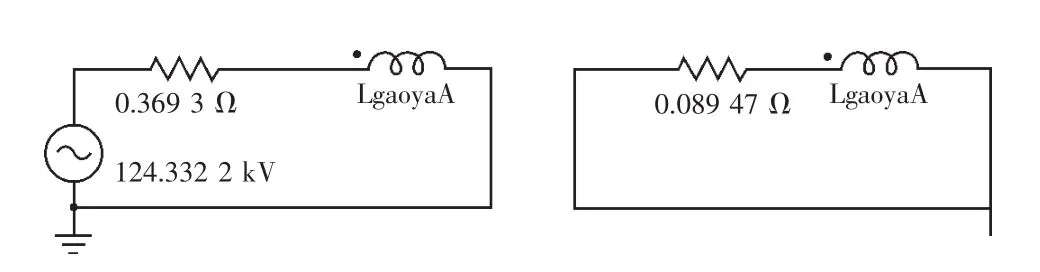
图2 场路耦合电路模型
由图2可见,激励的电压源为124.332 2 kV,此数据根据220 kV变压器短路试验时的电压波形得到,变压器三维场模型中的A相高压绕组等效为电路模型中的LgaoyaA,A相高压绕组的直流电阻为0.369 3 Ω。电压源、LgaoyaA和A相高压绕组的直流电阻串联,即得到高对中短路高压侧的电路模型,中压侧模型亦是同理得到。和变压器的工作原理一致,中压侧无电源,高压绕组、中压绕组通过变压器铁心建立两者的耦合关系,低压侧绕组通过变压器铁心磁通获得感应电势,该感应电势即为低压侧绕组的激励源。
场路耦合模型在计算过程中,变压器绕组既要参与三维电磁场模型的计算,又要参与外部电路模型的计算,只有同时满足这两种约束关系,才能得出准确的结果,场路耦合符合变压器的工作原理,因此场路耦合模型计算精度较高。
1.5 网格划分
Maxwell软件为用户提供了自适应剖分与手动剖分2种方式,自适应剖分很方便,但若仅采用自适应剖分其结果还是会产生一些瑕疵,而手动剖分时可以对不同的部件采用不同的剖分策略。以下采用手动剖分与自适应剖分相叠加的网格剖分策略,变压器绕组采用曲面逼近的剖分方式,该方法对于处理边界为曲线的物体效果较好;铁心、拉板、夹件、箱壳等结构件采用自适应剖分。
自适应剖分网格前,对部分结构采用手动剖分的策略可极大提升网格剖分效率,自适应网格剖分仅迭代了两步完成,第一次剖分后网格总量为2 177 302,第二次剖分后网格总量为2 830 989。能量误差、迭代能量误差变化率目标均为1%,完成第二次自适应剖分后能量误差、迭代能量误差变化率分别为0.046 795%和0.216 65%,网格质量较好,仿真模型最终网格总数为2 830 989,由于网格量巨大,仿真过程对服务器的配置要求较高,因此合理选择仿真时间步长将大大提升仿真效率。
2 数值模拟结果分析与讨论
2.1 A相高对中短路情况分析
通过瞬态场仿真可以观察不同时刻下变压器内部磁场的变化,由图3变压器铁心磁密分布云可以看出,变压器绕组电流达到峰值,即t=0.01 s时,A相旁柱铁心中部磁密约为1.688 3 T,A相主柱铁心中部磁密在0.377~0.450 25 T,B相铁心中部磁密约为0.900 44 T,C相主柱铁心磁密和C相旁柱铁心磁密数值更小。此时,铁心A相旁柱已饱和,A相主柱、B相主柱均未饱和。
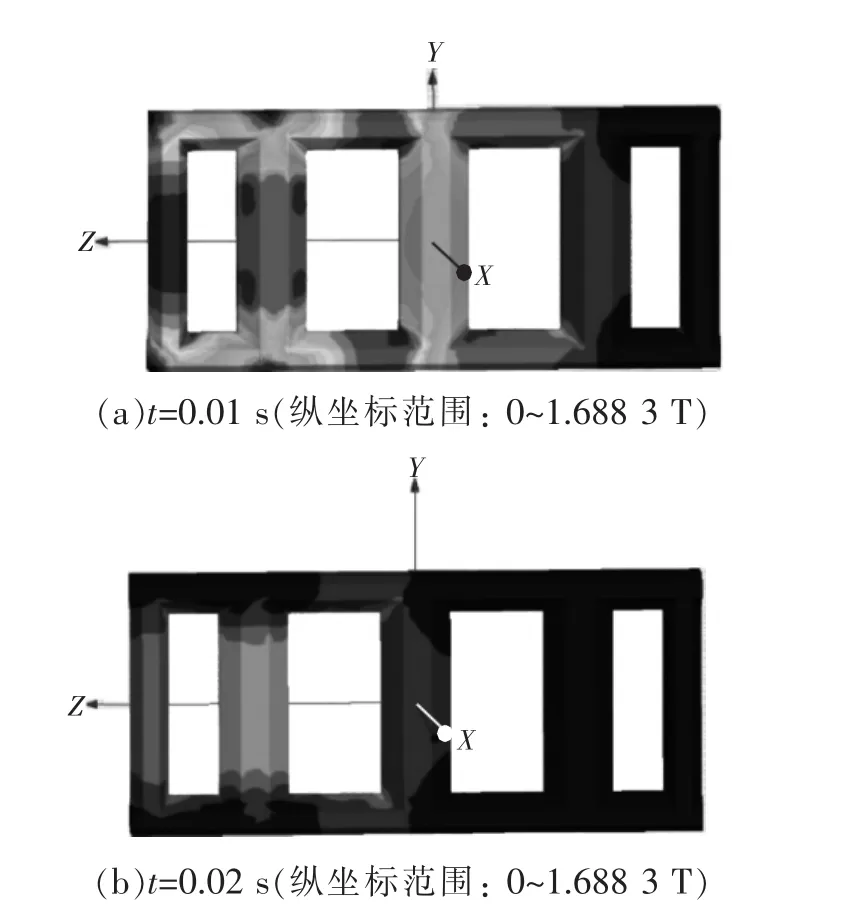
图3 不同时刻变压器铁心磁密分布云
A相旁柱铁心磁密高于B相主柱铁心磁密的原因是:该变压器铁心结构为三相五柱式,且A相旁柱与A相主柱的距离较B相主柱与A相主柱的距离小,因此其路径较短,磁阻较小,变压器A相短路时磁通主要经由A相旁柱闭合,因此A相旁柱磁密高于B相主柱磁密。同理,C相主柱和C相旁柱由于距离的原因,这两相铁心柱磁密较B相主柱磁密较小。
A相为短路相,但是A相主柱铁心磁密数值却较A相旁柱铁心磁密数值还要小,为了解释这一现象,以下将会在变压器内部漏磁场分布情况部分中予以详细说明。
由图4可知,t=0.01 s时,A相旁柱磁密矢量方向为逆时针方向,且幅值较大,B相主柱磁密矢量方向为顺时针方向;t=0.02 s时,A相旁柱磁密矢量方向改变为顺时针,且幅值较小,B相主柱磁密矢量方向改变为逆时针。这一情况的发生是变压器短路过程中短路电流衰减造成的,在t=0.01 s时,变压器A相高压侧短路电流为第1个正弦周期内的第1个峰值,幅值较大,且幅值为正;在t=0.02 s时,变压器A相高压侧短路电流为第1个正弦周期内的第2个峰值,幅值较小,且幅值为负。短路电流对变压器铁心起到励磁作用,当短路电流发生正负交替时,变压器铁心磁密矢量也发生方向变换,且铁心磁密幅值与绕组短路电流呈现出正相关特性。

图4 不同时刻变压器铁心磁密矢量分布云
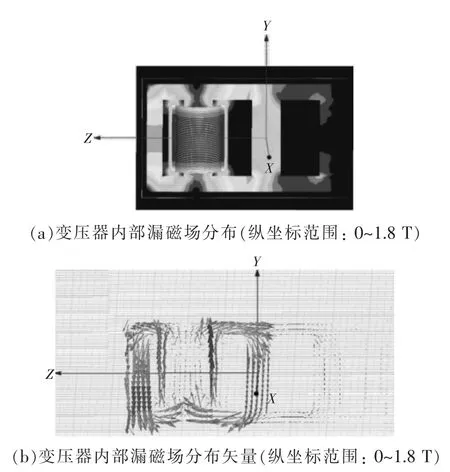
图5 变压器内部漏磁场分布
图5为t=0.01 s绕组电流达到峰值时变压器内部漏磁场分布情况,可以看出,变压器A相高压绕组与A相中压绕组之间主空道中的漏磁比较明显。主空道磁密可达1.8 T左右,比变压器A相旁柱、A相主柱和B相主柱的磁通大得多;且A相绕组经由铁窗气隙进入变压器上轭的漏磁幅值约为0.8 T。由图5(b)可以看出,变压器A相主柱磁密幅值较小,B相铁心磁通大部经由A相高中压绕组右部闭合;A相旁柱铁心磁通大部经由A相高中压绕组左部闭合。发生短路时,A相高中压绕组间漏磁严重,且A相高中压绕组对变压器上下铁轭漏磁严重,从而导致A相主柱磁密较小。
2.2 B相高对中短路情况分析
图6为t=0.01 s绕组电流达到峰值时变压器铁心磁密分布情况,可以看出,B相主柱磁密幅值小于A相主柱和C相主柱磁密,由于三相五柱变压器结构的对称性,A相、C相心柱磁密、磁密矢量几乎完全对称,主柱磁密幅值约为0.8 T,铁心拐角处磁密较高,最大值约为1.4 T。此时变压器主柱均未饱和,局部出现磁饱和(如铁心拐角处),随着短路电流的衰减,变压器铁心磁密也随之减小,因此在整个短路过程中,铁心不会出现磁饱和的情况。
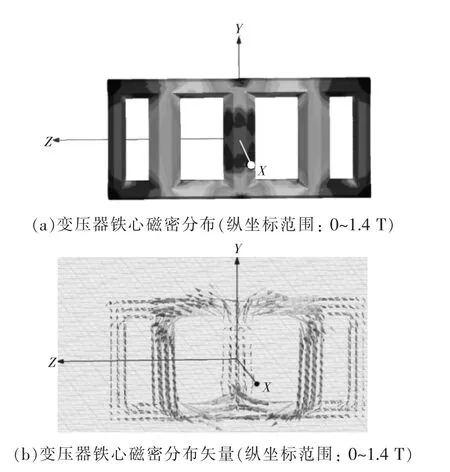
图6 0.01 s时变压器铁心磁密分布云
图7给出的变压器铁心磁密分布情况表明,由于三相五柱变压器的对称性,变压器内部漏磁场也呈现出对称性,B相高压绕组与中压绕组间空道磁密峰值约为1.5 T,中压绕组端部漏磁幅值约为0.7 T。
3 结论
采用ANSYS Maxwell 3D软件对220 kV油浸式三相电力变压器在短路状态下的三维瞬态电磁场进行数值模拟,得到了电磁场分布和电磁损耗情况,分析后得到以下结论:
(1)数值模拟结果表明,A相短路时,A相旁柱严重饱和,A相主心柱和B相主心柱均未饱和;B相短路时,变压器铁心柱均未发生饱和,仅在铁心拐角处造成轻微饱和。
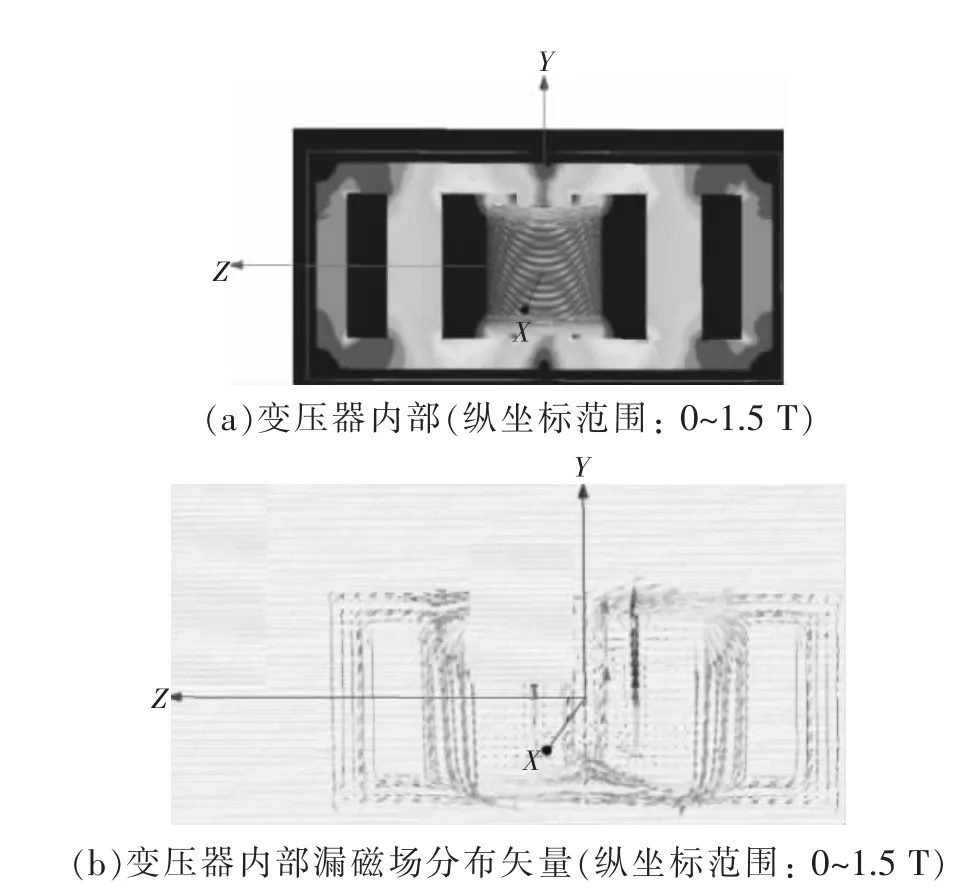
图7 0.01 s时刻变压器内部漏磁场分布
(2)变压器短路时,短路相绕组间、短路相绕组端部漏磁均比较严重。
(3)对于变压器铁心磁密、漏磁场等不可测或不易测量的参数,仿真结果具有较高的精度,有一定的应用价值。为今后进一步开展变压器短路问题研究提供了思路与方法,特别是为短路过程中绕组稳定性、变压器油流涌动等问题的研究提供了数据基础。
研究结果对于现场变压器在受到短路状态时,研究电磁场分布提供了重要的技术手段,对现场运行具有较好的指导意义。
[1]梁振光,唐任远.大型电力变压器绕组的短路强度问题[J].变压器,2003,40(8)∶9-12.
[2]尹克宁.电力工程[M].北京:北京水利电力出版社,1987.
[3]王世山,李彦明.电力变压器绕组电动力的分析与计算[J].高压电器,2002,38(4)∶22-25.
[4]朱占新,谢德馨,张艳丽.大型电力变压器三维漏磁场与结构件损耗的时域分析[J].中国电机工程学报,2012,32(9)∶156-160.
[5]汲胜昌,张凡,钱国超,等.稳态条件下变压器绕组轴向振动特性及其影响因素[J].高电压技术,2016,42(10)∶3178-3187.
[6]朱德恒,谈克雄.电气设备状态监测与故障诊断技术的现状与展望[J].电力设备,2003,4(6)∶1-8.
[7]李冰阳,臧春艳,徐肖伟,等.电力变压器抗短路能力校核研究[J].高电压技术,2015,41(S)∶112-116.
[8]孙翔,何文林,詹江杨,等.电力变压器绕组变形检测与诊断技术的现状与发展[J].高电压技术,2016,42(4)∶1207-1220.
[9]鲁非,金雷,阮羚,等.电力变压器轴向位移故障诊断方法[J].高电压技术,2016,42(9)∶2916-2921.
[10]刘文里,唐宇,李赢,等.电力变压器高压绕组辐向稳定性评估[J].哈尔滨理工大学学报,2016,21(4)∶90-95.
[11]李洪奎.大型电力变压器绕组短路强度与稳定性研究[D].沈阳:沈阳工业大学,2011.
[12]张明丽.大型变压器抗短路能力校核研究[D].武汉:华中科技大学,2012.
[13]王欣伟,连建华,俞华,等.电力变压器内绕组辐向抗短路能力的计算与分析[J].变压器,2013,50(1)∶8-11.
[14]李敏堂,严萍,袁伟群,等.强流脉冲对结构体冲击力的数值模拟及试验[J].强激光与粒子束,2010,22(3)∶659-663.
[15]孙昕.短路与重合闸工况下大容量电力变压器绕组强度研究[D].沈阳:沈阳工业大学,2015.
[16]李帅.10 kV级油浸式配电变压器漏磁场和抗短路能力的研究[D].天津:河北工业大学,2015.
[17]王伟.大型电力变压器应力场和漏磁场的有限元分析[D].保定:华北电力大学,2014.
[18]闫学勤,杜勇,梁岚珍.基于ANSYS的电力变压器铁芯磁场与漏磁场分布的仿真研究[J].新疆大学学报(自然科学版),2005,22(3)∶361-364.
[19]张涛,周凯,周承鸣.基于ANSYS的电力变压器三维磁场分析[J].西华大学学报(自然科学版),2008,27(5)∶7-9.
[20]李占强.电力变压器结构件漏磁场和温度场的分析与研究[D].天津:河北工业大学,2009.
[21]陈湘令.基于Ansoft的变压器突发短路有限元漏磁场分析[J].电气技术,2015(3)∶61-62.
[22]张丙旭.提高变压器承受短路能力的实验研究[D].保定:华北电力大学,2010.
[23]刘东升,张俊杰,赵峰,等.特高压特大容量变压器三维涡流场计算和防止局部过热技术的研究[J].变压器,2009,46(9)∶1-5.
