基于贝叶斯准则的非侵入式负荷监测方法
2018-06-11周晨轶闫娇娇刘晨阳
周晨轶,闫娇娇,刘晨阳
(国网浙江省电力有限公司信息通信分公司,杭州 310007)
0 引言
居民用户是坚强智能电网的重要消耗端,也是微电网的重要组成部分。负荷监测技术可以帮助用户了解家中电器使用情况,提高用户参与需求响应的意识,促进用户科学合理用电[1-2]。此外,在电力需求侧管理、盗电监管、实时电价等多个智能电网的应用领域,负荷监测技术都起到了重要作用[3-5]。目前,负荷监测技术主要分为侵入式和非侵入式2种[6]。侵入式负荷监测需要在总负荷内部的每个用电器上都配备传感器,该方法虽然准确性高,但可靠性低,实施困难;非侵入式负荷监测只需在用户的用电入口处安装1个传感器,通过分析监测得到的总负荷数据,来获知用户各用电设备的工作状态,该方法成本低,安装方便,是近年来负荷监测技术的研究重点。图1描述了NILM(非侵入式负荷监测)技术在需求响应系统中的作用。
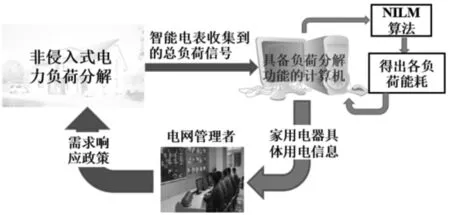
图1 NILM技术在需求响应系统中的应用
NILM技术又称负荷分解技术,最初是由麻省理工的Hert教授于20世纪80年代提出的[7]。他根据不同设备开关时总负荷功率变化量的不同,实现了负荷的辨识和分解,针对具有多工作模式的电器,提出了基于有效状态机的负荷识别方法。
与Hart利用稳态特性进行负荷识别不同,另一类NILM技术依据设备暂态投切特性的不同进行负荷辨识,如基于V-I曲线特性的分析方法[8]、基于瞬时无功功率的分析方法[9]、基于暂态功率谱的分析方法[10]、基于电流谐波特性的分析方法[11]等。相较基于负荷稳态特性的分析方法,基于暂态投切特性的分析方法能够获得更加丰富的电器信息,进而提升负荷辨识的准确率。然而,这类方法的实现需要监测设备具有极高的采样频率,现有的常规电力设备无法满足要求。
最近很多NILM研究都是在低采样频率(小于1 Hz)的前提下,通过一种或几种监测方法得到总负荷特征参数(如电流、功率)并进行分析,实现居民用电负荷的辨识和分解[12-14]。Zeifman[12]为提高负荷识别的准确率和程序的运算速度,将Viterbi译码算法应用于NILM系统中,但该方法只对简单开关类电器有效。文献[13]根据电器不同工作状态下长时段负荷曲线的差异性,提出基于进制拟合算法的负荷分解方法,在一定程度上解决了多工作模式负载投入使用的负荷识别问题。然而,由于绝大多数家用电器长时段运行的负荷曲线受环境、人为等因素的影响很大,使文献[13]中的方法只对极少部分电器有效,具有很大的局限性。Dinesh等[14]为提高负荷分解的准确率,对采集得到的低频负荷数据进行K-L(Karhunen Loeve)变换,进而提取并利用数据中隐含的谱信息,然而,当数据量较大时,K-L变换大大降低了程序的运算速度和效率。
针对上述负荷分解方法的不足,同时结合现有电力监测设备的特点,提出基于贝叶斯准则的NILM方法。该方法的显著优点是对监测设备采样频率要求低、算法简单、可准确分解各类型电器的用电负荷。首先,搭建一套有效的用电信息采集演示系统,方便建立模型及开展验证工作;而后,提出负载电流概率密度函数的概念,并在此基础上提出了基于贝叶斯准则的负荷分解模型;最后,给出基于DE(差分进化)算法的模型求解思路,并使用实测数据进行算法验证。
1 负荷数据的采集
NILM技术研究的关键一点便是要建立家用电器的负荷数据集,为此,在室内搭建一套长期有效的用电数据采集系统。每个用电器都通过转换插头与一个基于ZigBee协议的通用智能电表相连,以便获取各用电器的用电数据;所有的用电器都被连接在同一个插线板上,以便获取总电流数据。表1列出了智能电表能够测量到的所有用电参数。在采样频率为1/60 Hz的情况下(每隔1 min返回1次信息),采集了5种典型家用电器1个月的用电数据,包括饮水机、电冰箱、微波炉、空气净化器和电热水壶。这些电器的工作原则与实际家庭中类似,例如,饮水机和电冰箱一般会连续运行一整天,空气净化器在空气质量不好的情况下工作频率更高。
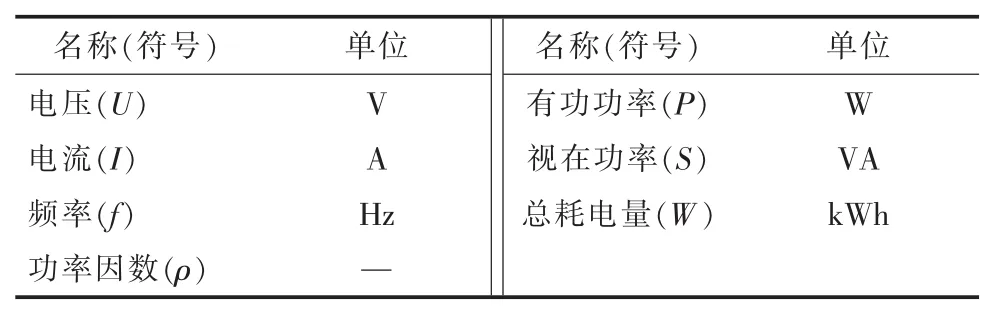
表1 智能电表监测的用电参数
此外,在PC端安装了2个相关软件,分别是MySQL(一种数据库管理系统)和PMS(能量管理系统)。前者用于存储和管理搜集到的历史数据;后者是一个用电数据演示系统,能够实时显示各用电器的用电信息,以便确认各个智能电表是否处于正常工作状态。图2是用电数据演示系统的示意。
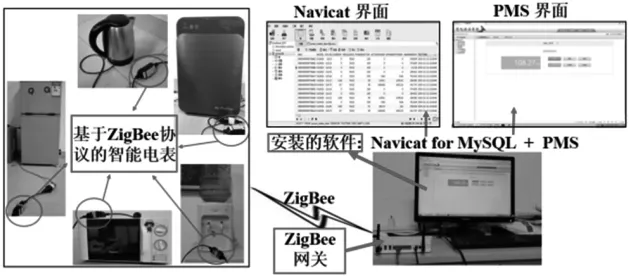
图2 用电数据演示系统示意
2 基于贝叶斯准则的负荷分解模型
先前相关研究表明[5],与电器的有功功率相比,电器电流幅值的波动更小,因此利用稳态电流作为负荷特征更容易确定电器的工作状态。在构建模型之前,可以确定智能电表采集到的数据具有以下特点:
熊定喜 男,1992年出生于湖北松滋.现为北京空间信息中继传输技术研究中心助理工程师,主要研究方向为导航信号质量评估技术和卫星轨道控制技术.
(1)电流数据是离散的。
(2)电流幅值不可能为负数,最小值为0。
(3)针对文中的采集系统,电流幅值的上限由插线板的额定电流决定(实际家庭中由断路器的额定电流决定,超过额定电流会自动跳闸)。
2.1 数据预处理
假定n个独立离散的随机变量XR-I(1),XR-I(2), …, XR-I(n), 其中 XR-I(i)表示用电器 X 在第i个采样点的原始电流幅值,对应预处理之后的电流值 XI(i)表示为:

式中:[]表示取整,[x]表示不超过x的最大整数;i∈{1, 2, …, n}, XI(i)∈{0, 1, …, M}, 文中 M的值由插线板的额定电流值决定。例如,若所有电器共同连接在额定电流为15 A的插线板上,那么M=150。经此转换,电流幅值单位由A(安培)变为dA(deci-Ampere),并且全部转换为正整数。
2.2 基于贝叶斯准则的负荷分解数学模型
贝叶斯准则,又称贝叶斯信息准则,是在不完全信息下,对部分未知的状态用主观概率估计,然后用贝叶斯公式对发生概率进行修正,最后再利用期望值和修正概率做出最优决策。基于此,在确定求解目标前,先定义离散概率密度函数PDF:

式中:P[XI=x}表示监测数据中用电器X预处理后的电流幅值为x的概率,其值根据采集得到的训练数据计算得出,如果训练数据的总个数为n,电流幅值为x出现的次数为k,那么有P[XI=x}=k/n。例如,以1 000个采样点为例,表2是工作电流为0.3 A的电器可能的PDF值。
NILM技术解决的问题可以表述为:如何根据采集得到的总负荷数据(如总电流、总功率),确定其中每个电器的运行状态和能耗。众所周知,负荷总电流值SI可以表示为:

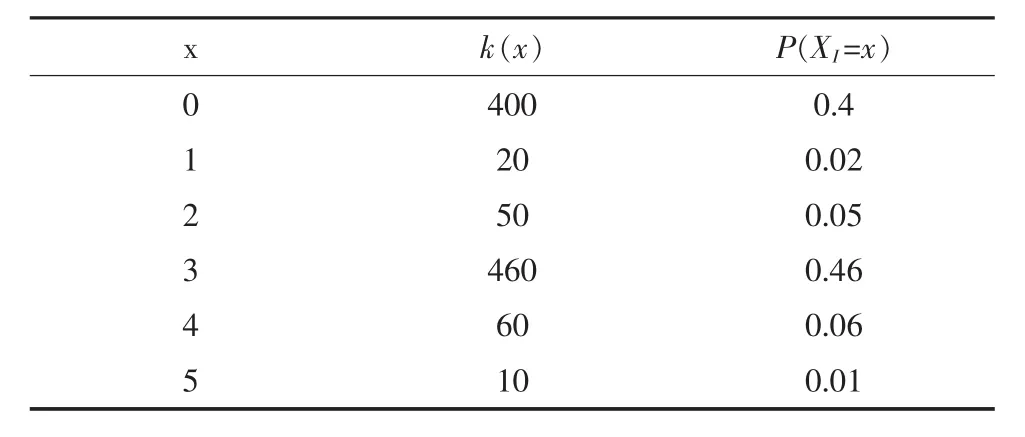
表2 一个关于PDF值的例子
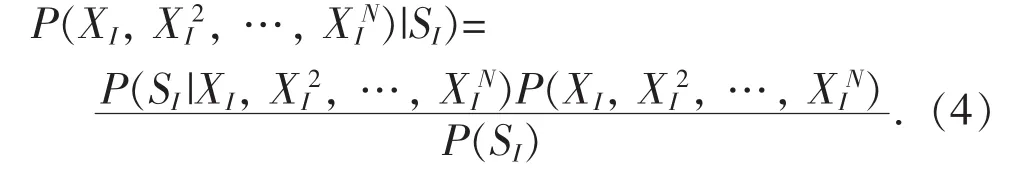
式(4)中 P(SI|XI, XI2, …, XIN)为条件概率,由于必然存在至少一种组合使得总电流值为SI,故 P(SI|XI, XI2, …, XIN)的值恒为 1, 因此式(4)可化为:
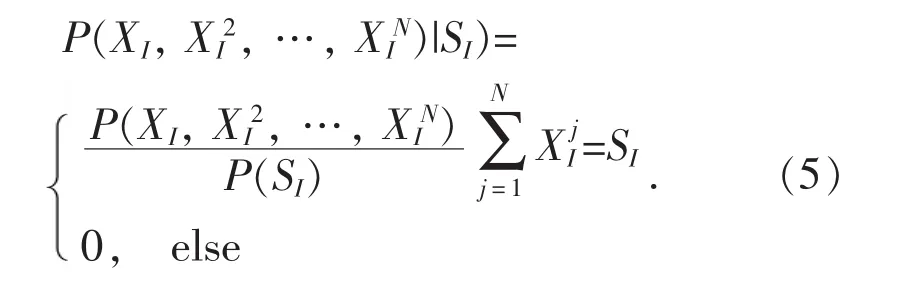
对于任意一种组合,P(SI)的值都是相同的。此外,不同电器之间的开关可认为是相互独立的,因此式(5)的最大后验概率解可以表示为:寻找满足条件的、最有可能的电器开关组合,也就是说使得 P(XI,,…,)值最大。不难发现,的最小值为因此, NILM 方法的求解目标可表述为,寻找一种电器组合使得Z的值最小(argmin(Z)), 其中:
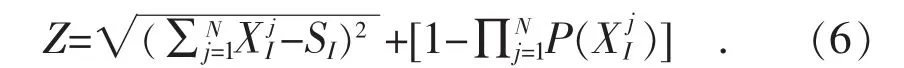
2.3 DE算法
DE算法是一种比较新的基于群体的随机优化方法,在求解最小值问题上具有更好的收敛性和鲁棒性[5]。图3是DE算法的求解流程,主要求解步骤分6步。
步骤1:确定种群规模(一般取10倍于问题规模数)、迭代次数和电器电流值可能的进化范围。
步骤2:生成初始种群。设第i个个体,Xi=(xi,1, xi,2, …, xi,n), n 为种群的规模。 一般个体向量Xi各个分量的产生方式为:
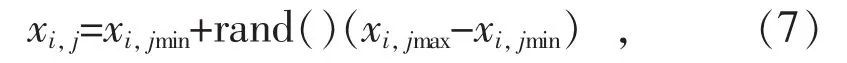
式中: xi,j是 Xi的第 j个分量, xi,j的范围是[xi,jmin,xi,jmax]。
步骤(3):变异。对于第k代的目标向量,DE算法变异向量的产生方式如下:

式中:F为变异因子,一般取值范围为[0.4,0.9]。
步骤4:交叉。DE算法中有2种常用的交叉方式,分别是二项式交叉和指数交叉。文中采用的是二项式交叉方法,对于第k代目标向量其各个分量的计算方法为:
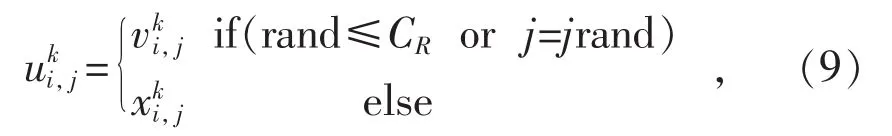
式中:CR为交叉因子;rand是[0,1]之间的随机数,jrand是[1,n]之间的随机整数。
步骤5:取整。由于DE算法进行的是全局搜索,而采样数据之间是离散的,因此在进行选择操作之前,先通过四舍五入取整运算对参数进行取整。
步骤6:选择。DE算法中使用的是“贪婪”选择模式,也就是说,只有当新个体能够得到更小的Z值时才能够被保留下来。
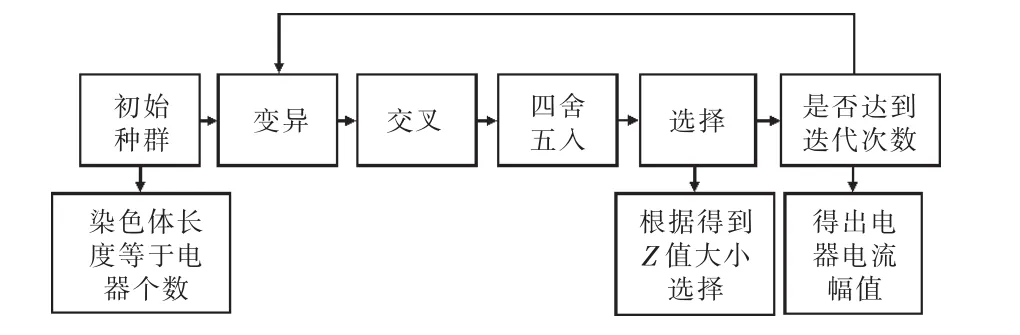
图3 DE算法求解流程
3 算法评估和验证
3.1 算法评估方法
NILM技术的目标有2个:一是让用户能够了解家中电器的具体能耗,这能够指导居民科学合理用电;二是让用户能够近乎于实时地了解家中电器的工作状态,这对电力公司制定更加细化的需求响应政策非常重要。为评估所提出算法有效性,Kolter和Johnson[15]提出了能耗评估精度Est.Acc的概念,计算公式如下:
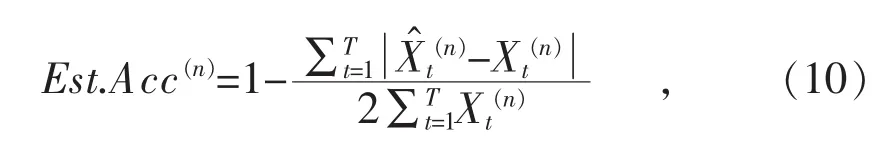
3.2 验证结果
以下利用用电信息采集系统收集到的数据进行算法验证工作。采集到5种家用电器1个月的用电数据,其中前25天的数据用于训练,以便确定用电器的PDF;后6天的数据用于测试,评估所提出算法的有效性。详细的模型评估流程如图4所示。
所有算法验证程序都是基于MATLAB 2013a,程序运行在具有2.2 GHz CPU和1 GB内存的电脑上。DE算法的训练次数为500,变异因子和交叉因子取值都为0.5,表3为算法验证结果。

表3 算法估算精度
根据表3发现,文中所提算法能够分解包括多状态模式在内的各种用电设备。对于经常使用的(如电冰箱、饮水机)或是电流幅值相对较大的(如电热水壶、微波炉)用电器,文中所提出算法的能耗评估精度值都达到90%以上。对于电流幅值较小的电器(如空气净化器),该方法的分解精度不够理想。
3.3 电器能耗计算方法
有了各个电器在每个采样点的分解电流值后,可以得到电器每小时耗电量的计算公式:
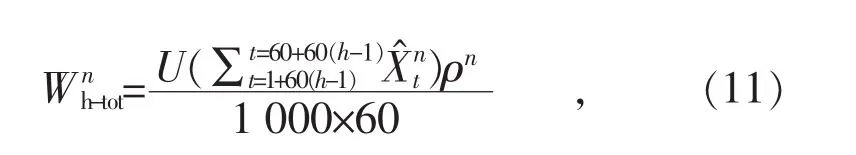
式中:为电器n每小时的耗电量;为电器n在t时刻的估算电流值;ρn为电器n的功率因数;U为家庭电压;h为时间参数,且 h∈[1,2,3, …, 24]。
表4给出了采用NILM方法计算得到的用电器月能耗。
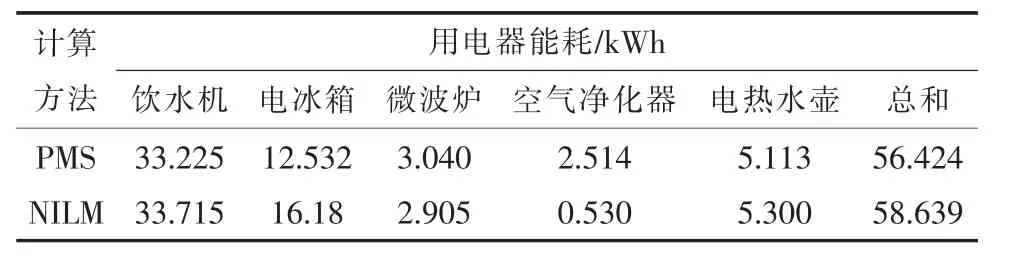
表4 采用NILM方法得到的各用电器月能耗
由表4可知:若以传统用电信息演示系统监测(侵入式方法,图2中PMS)得到的用电数据为基准,则采用NILM方法对总能耗的估算误差为:

4 结论
(1)提出了基于贝叶斯准则的负荷分解模型,该模型将NILM问题转化为数学上的求最小值问题。利用室内实测用电数据进行算法验证工作,证明所提供方法的有效性和准确性。
(2)NILM模型建立时,充分利用监测所得历史数据,提出用电器PDF的概念和计算方法;此外,在模型求解时利用了DE算法,其他能够求解最小值的优化算法同样适用。
(3)给出了一种非侵入式能耗估算方法,并与传统侵入式负荷监测方法进行比较,证明了文中所提方法的准确性。
(4)文中方法所需用电数据可直接由市面上通用的智能电表获得,降低了硬件成本,提高了用户参与需求响应的积极性。此外,由于居民电力负荷组成最为复杂,文中所提方法也适用于工业和商业负荷的监测和分解。
[1]林弘宇,田世明.智能电网条件下的智能小区关键技术[J].电网技术,2011,35(12)∶1-7.
[2]王蓓蓓,李杨.面向智能电网的电力需求侧管理规划及实施机制[J].电力自动化设备,2010,30(12)∶19-24.
[3]张文亮,刘壮志,王明俊,等.智能电网的研究进展及发展趋势[J].电网技术,2009,33(13)∶1-11.
[4]宋亚奇,周国亮,朱永利.智能电网大数据处理技术现状与挑战[J].电网技术,2013,37(4)∶927-935.
[5]周晨轶,刘松,钟潇,等.基于差分进化算法的居民用电负荷分解方法[J].南方电网技术,2016,10(6)∶62-69.
[6]余贻鑫,刘博,栾文鹏.非侵入式居民电力负荷监测与分解技术[J].南方电网技术,2013,7(4)∶1-5.
[7]HART G W.Nonintrusive appliance load monitoring[J].IEEE Proceeding,1992,80(12)∶1870-1891.
[8]HASSAN T,JAVED F,ARSHAD N.An empirical investigation of V-I trajectory based load signatures for non-intrusive load monitoring[J].IEEE Transactions on Smart Grid,2014,5(2)∶870-878.
[9]曲朝阳,于华涛,郭晓利.基于开启瞬时负荷特征的家电负荷识别[J].电工技术学报,2015,30(S1)∶358-364.
[10]CHANG H H,LIAN K,SU Y,et al.Power-spectrumbased wavelet transform for non-intrusive demand monitoring and load identification[J].IEEE Transactions on Industry and Application,2014,50(3)∶2081-2089.
[11]SRINIVASAN D,NG W S,LIEW A C.Neural-networkbased signature recognition for harmonic source identification[J].IEEE Transactions on Power Delivery,2006,21(1)∶398-405.
[12]ZEIFMAN M.Disaggregation of home energy display data using probabilistic approach[J].IEEE Transactions on Consumer Electronics,2012,58(1)∶23-31.
[13]娄建楼,于华涛,曲朝阳.面向家庭用户的用电负荷分解方法[J].吉林大学学报(理学版).2015,53(4)∶744-753.
[14]DINESH C,NETTASINGHE B W,GODALIYADDA R I,et al.Residential appliance identification based on spectral information of low frequency smart meter measure ments[J].IEEE Transactions on Smart Grid,2016,7(6)∶2781-2792.
[15]KOLTER J Z,JOHNSON M J.REDD∶A Public Data Set for Energy Disaggregation Research[C].Sustkdd,San Diego,CA,USA,2011.
[16]颜庆国,阮文骏,陈楚,等.基于并行预测策略的公共楼宇日前空调负荷预测[J].电网与清洁能源,2016,32(11)∶80-86.
