地震作用下深水桥墩动水压力分析方法研究
2018-06-09刘建军刘利果陈杰群卢志刚张秀芳吕章元
刘建军 刘利果 陈杰群 卢志刚 张秀芳 吕章元
1 引言
随着我国经济实力的增强,大型桥梁、港口码头、海洋石油平台等工程的建设对促进国民经济的发展起到了重要的作用,而这些工程均建在水中,在地震作用下,水体受地震激励后将产生剧烈的波动,这种波动对水中墩柱结构地震反应的影响被称为动水压力效应。从力学角度分析,动水压力效应的主要体现在于水体波动对墩柱施加的动水压力,且动水压力直接形成了墩柱的附加荷载。
与空气中的桥梁相同,抗震问题也是深水桥梁不可回避的,深水桥梁在地震作用下会引起结构周围水体的辐射波浪运动,由于结构与水的相对运动,在结构水下部分将作用有动水压力。该动水压力不仅会改变结构的动力特性,还会影响结构的动力响应。
在地震作用下,处于深水中的桥墩会发生一定振动和变形,并引起周围水体的晃动,水体又以动水压力的形式反作用于桥墩,改变桥梁墩身的振动和变形状态,这种作用与反作用伴随地震动作用过程的始终。我国有许多在建和拟建的深水桥梁。对于这类深水桥梁,在抗震分析中需要考虑动水压力的影响。我国《铁路工程抗震设计规范》规定:梁式桥跨结构的实体桥墩,在常水位以下部分,水深超过5m时,应计入地震动水压力对桥墩的作用。目前,在海洋平台、大坝、码头等近海工程的抗震分析中都考虑了水对结构的影响,而在桥梁抗震分析领域,这方面的研究工作还不多。
2 动水压力的分析方法
2.1 规范法
我国《铁路工程抗震设计规范》规定,当水深超过5m时,对于圆形或圆端形实体桥墩,水中高度hi处单位墩高的动水压力计算公式:

式中:
FiwE——水中墩高度hi处单位墩高的动水压力(kN);
mw——桥墩单位高度水的附加质量(t/m),
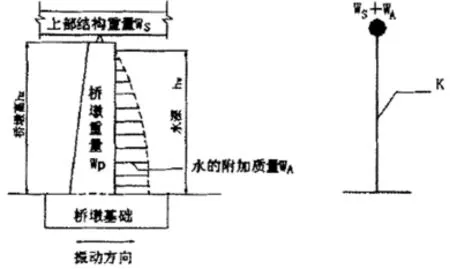
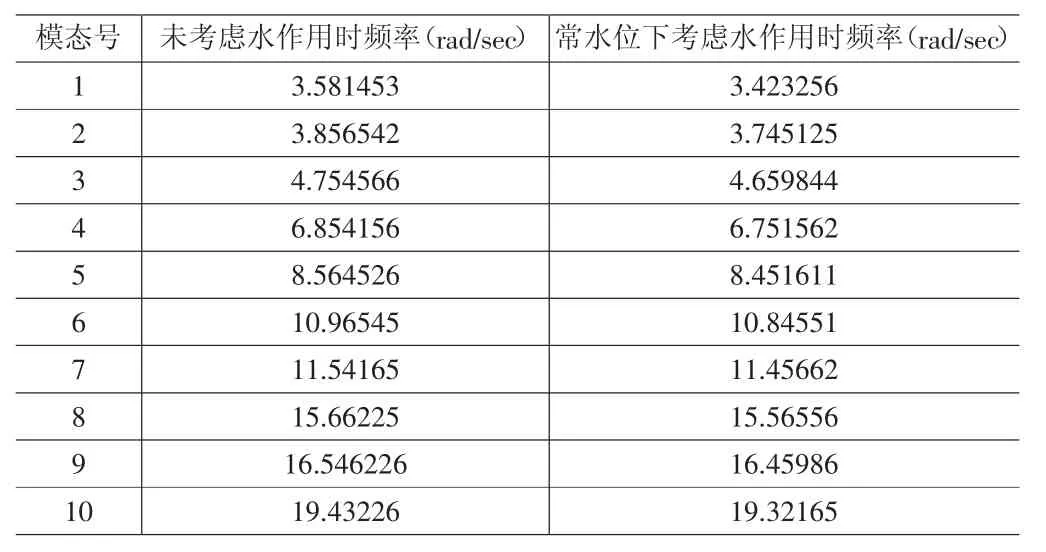
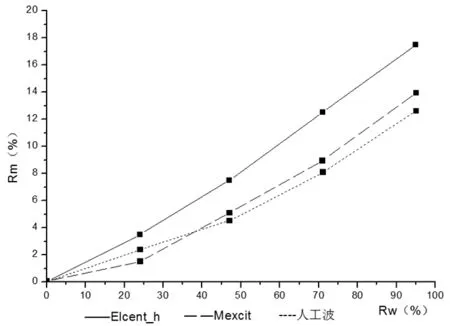
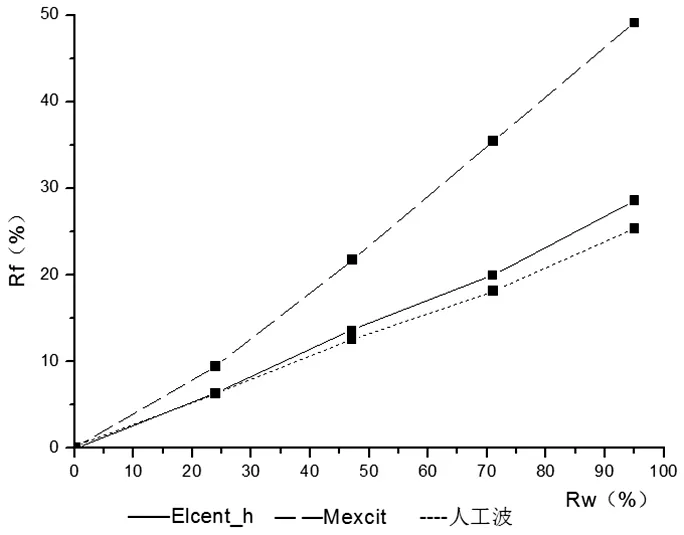
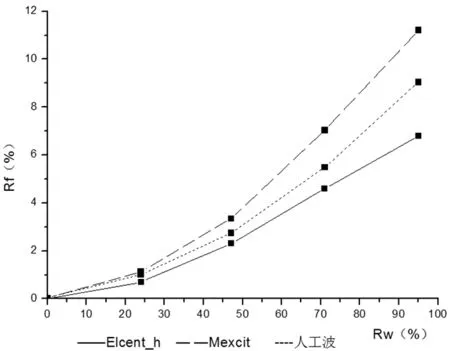
当0 当0.8hw W——水的重力密度(kN/); A——以垂直于计算方向,桥墩hW/2处的截面宽度为直径的圆面积(m2); γ1——桥墩计算方向的振型参与系数; β1——桥墩计算方向的动力系数。 由于水的影响,γ1和 β1都将改变,γ1、T1按下式计算: 墩底剪力、弯矩按下列公式计算: 规范方法是以反应谱理论为基础,在计算深水桥墩的地震响应时,桥墩的自振特性不变,动水压力以及其在墩底产生的剪力、弯矩单独计算。动水压力采用了附加质量的计算模式,由于动水的影响,桥墩结构的基本自振周期T1及振型参与系数γ1都将改变,可按式3和式2计算,以此为基础,可以求出作用在桥墩上的动水压力及墩底剪力、弯矩。 目前,在众多流固耦合问题分析方法中,采用附加质量法计算地震作用下动水压力对结构物的影响已经得到了广泛的认可。 地震荷载作用的加速度激励是随时间不断变化数值和方向的,桥墩产生与之相应的往复加速晃动,液体与桥墩侧面之间产生大小和方向也不断变化的相对惯性作用力以及相对滑动。Westergaard对此类问题提出了简化形式的附加质量法并认为,液体对桥墩侧面某点处产生的动水压力,等效于在这点附加一定质量的液体与桥墩一起运动而产生的惯性力,而不再考虑除此之外的其他部分液体在这点处对桥墩动水压力的贡献。这是一种解耦的算法,为分析此类工程问题提供了方便。动水压力的特点与惯性力相似,所以Westergaard提出可以用附着在坝面的一定质量的水体来代替水的动力学效应。根据惯性力与坝面动水压力相等的条件,可得Westergaard附加质量公式: 其中h为水位高度,y是以水面为原点的竖向坐标。 以上的Westergaard的附加质量公式目前在美国和日本的建筑抗震设计中还在广泛使用。 在桥梁的抗震设计中,用结构地震反应分析进行桥梁下部结构的计算时,将由于动水压力引起的附加质量加到运动方程式的外力项中来考虑动水压力的总的影响(如图1所示)。 图1 附加质量的设计简图 不考虑附加质量时的运动方程为: 考虑附加质量MA后的运动方程式: 上面两式分别为将附加质量计入外力项和未将附加质量记入外力项的运动方程。 采用Morison方程来分析地震动水压力对深水桥墩的影响,即以Morison方程为基础,把水等效为附加质量来考虑水对结构的影响,再采用有限元方法计算桥墩结构的地震响应。该方法是一种可用于大型桥梁结构深水桥墩抗震设计的时程分析方法。 忽略桥墩对水运动的影响,认为水对桥墩的作用由未受扰动的加速度场和速度场引起的沿水运动方向作用于桥墩上的惯性力和阻尼力所引起,采用简化的Morison方程表示地震动引起的桥墩动水压力: 式中,ρ为水的密度,V为水下桥墩结构体积,AP为桥墩截面面积,u¨、u˙分别为水的绝对加速度和绝对速度,x¨、x˙分别为桥墩的相对加速度和相对速度,x¨g为地震动加速度,CM为动水惯性力系数,CD为动水黏性阻尼系数。 假设桥墩处于静水之中,即u¨=u˙=0,式(10)简化为: 式(11)右端第二项为非线性项,将该项线性化处理,得到线性Morison方程。 式中,σx˙+x˙g为结构绝对速度的标准差。令 MW=(CM-1)ρV 为动水附加质量系数为动水附加阻尼系数。 由于动水阻力引起的桥墩结构的动力相应变化率很小,为简化计算,可以忽略CW的影响,则式(13)简化为: 可以看出,与不考虑动水压力影响的动水平衡方程相比,考虑动水压力影响时,动力平衡方程的形式不变,只是在质量矩阵M上附加了矩阵MW。因此,考虑动水压力影响(有水)与不考虑动水压力影响(无水)的结构体系地震反应的分析方法是一致的。 假定桥墩两相邻单元中点之间水与桥墩的相对速度不变,且作用在桥墩第i个节点的作用力为与i点相连的构件受力总和的一半,即每个节点只承受单元受力的一半,则节点i处等效附加水质量为: 式中,j为与节点i相邻的节点,lij为第ij单元有效长度的一半。 应用Morison方程正确计算动水压力的关键问题之一是合理选取动水惯性力系数CM。一般认为CM同雷诺数、Kculegan-Carpenter数及结构表面相对粗糙度有关。为使用方便,各国相对规范都对CM的取值范围提出建议,对于圆柱体结构,CM=2.0。 则整个体系在地震动作用下的动力平衡方程可以表示为 某大桥5号、6号桥墩位于深水之中,为直径5m的圆形截面实体桥墩,墩高分别为12.72m和12.37m。此桥按基本烈度七度设防。 采用大型有限元计算软件MIDAS进行时程分析,在Morison方程的基础上,用附加水质量法考虑地震动水压力对桥墩的影响。 本文采用三类地震波对结构进行激励,三类地震波加速度峰值均调整为0.1g,采用一致激励方式进行激振。三类地震波加速度时程及其谱特征如图2所示。 图2 三类地震波特性及阻尼比为0.05时的反应谱 表1 浏阳河桥特征值分析 在上述计算模型的基础上,运用有限元程序计算了该大桥的自振特性。表1中列出了模型前10阶振型的频率与周期计算结果。 表2 水深对浏阳河大桥-阶频率的影响 表2列出了水深分别为0m、3m、6m、9m和12m时该大桥一阶频率的数值。从中可以看出,随着水深的增加,一阶频率在逐渐变小。 图3~5用无量纲参数列出了不同地震波作用下动水压力对墩顶位移和墩底内力的影响程度。其中RW表示相对水深,Rd、Rf和Rm分别表示动水压力对墩顶位移、墩底剪力和墩底弯矩的影响率,定义如下: 图3 地震波作用下地震动水压力对墩顶最大位移的影响程度 图4 地震波作用下地震动水压力对墩顶最大剪力的影响程度 由以上的计算结果可以看出,地震动水压力对桥墩结构的地震响应有较大的影响,随着水深的增加。计算项目不同,动水压力的影响程度也不同。从以上的计算结果来看,动水压力对墩底剪力的影响最大,对墩底弯矩的影响最小。 图5 地震波作用下地震动水压力对墩顶最大弯矩的影响程度 《铁路抗震设计规范》中规定,在水深大于5m时,要计算动水压力对桥墩的影。从图可知,如果在桥墩高度一定,水深不同的情况下,水的相对深度会不同,其对桥墩地震响应的影响程度也不同。因此,采用相对水深来决定在抗震设计中是否考虑地震动水压力对桥墩的影响更为合理。 本文采用附加质量法对大桥深水桥墩进行了地震响应分析计算,得出了一些有益的结论: (1)动水压力对桥墩的位移和内力均有影响,在进行抗震设计时考虑动水压力的作用是十分必要的。 (2)采用相对水深来决定是否考虑地震动水压力对桥墩的影响更为合理。 (3)动水压力对桥墩地震响应的影响程度与计算项目,水的深度,输入的地震记录等诸多因素有关。 (4)验证了附加质量法在深水桥墩地震响应分析中的有效性。 [1]李国豪,主编.桥梁结构稳定与振动.北京:中国铁道出版社,1992. [2]范立础,胡世德,叶爱君.大跨度桥梁抗震设计.北京:人民交通出版社,2001. [3]范立础.桥梁抗震.上海:同济大学出版社,1997. [4]高学奎,朱晞.地震动水压力对桥墩的影响.北京交通大学报,2005,5. [5]王志华,曹伟,陈国兴.考虑流固耦合效应的深水桥墩地震反应分析.防灾减灾工程学报,2010,10. [6]刘振宇,李乔,赵灿晖,庄卫林.圆形空心深水桥墩在地震作用下的附加动水压力.西南交通大学报,2005,4. [7]J.F.威尔逊.海洋结构动力学.北京:石油工业出版社,1991. [8]中华人民共和国铁道部.《铁路工程抗震设计规范》(GBJ111-87)[S].北京:中国计划出版社,1988. [9]邱大红.波浪理论及其在工程中应用.北京:高等教育出版社,1985. [10]Hogben N,“Wave loads on structures”,Proceeding of 1stBoss Conference,1976.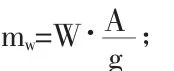
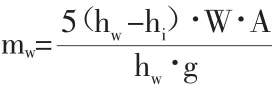


2.2 附加质量法




2.3 Morison方程法






3 工程实例分析
3.1 地震波输入
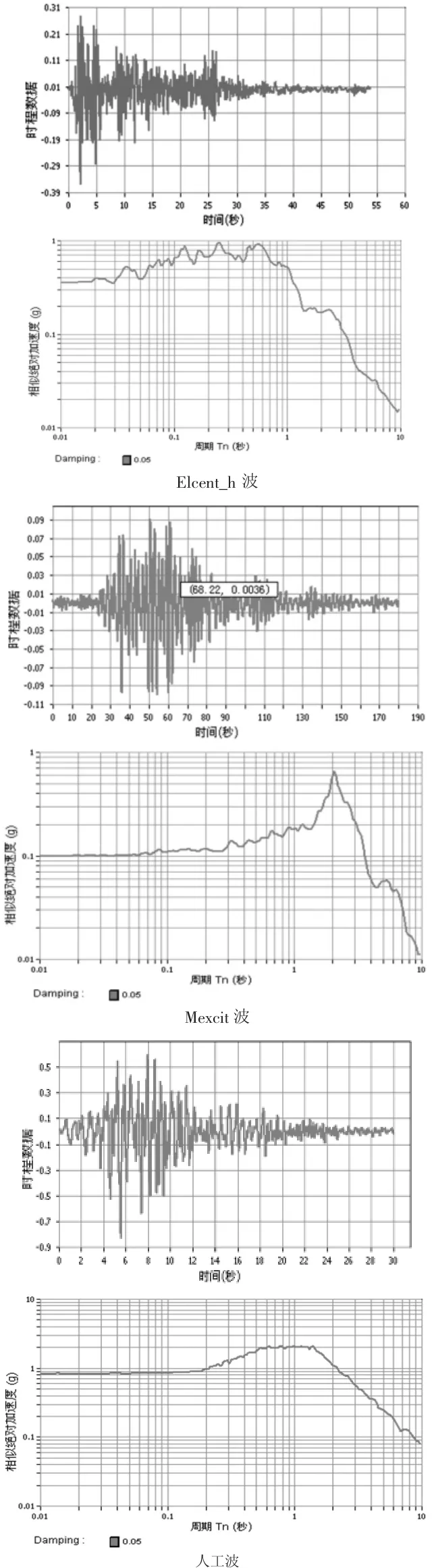

3.2 计算算结果
3.3 桥墩地震响应分析

4 结论
