基于自适应网格的隐私空间分割方法

张啸剑 金凯忠 孟小峰

1(河南财经政法大学计算机与信息工程学院 郑州 450002) 2 (中国人民大学信息学院 北京 100872) (xjzhang82@ruc.edu.cn)

信息时代的飞速发展，空间数据的获取与收集变得尤为容易，例如移动用户位置、GPS位置、家庭住址等数据.通过对空间数据的分析，使得交通监控、位置推荐等应用能够提高自身的服务质量.然而，空间数据蕴含着丰富的个人敏感信息，在提供给第三方应用的同时，个人的敏感信息有可能被泄露.因此，如何在隐私保护的前提下，发布空间数据是当前基于位置服务的主要挑战问题.匿名化[1]与差分隐私[2-4]是常用的隐私保护模型.然而，匿名模型由于对攻击背景知识与攻击模型给出过多特定假设，而不适合真实的位置服务.例如，文献[5]指出在给出150万条匿名后的用户位置数据，在无任何背景假设情况下，随机给出2个时空点，能够甄别出50%用户的敏感位置，随机给出4个时空点，能够甄别出97%用户的敏感位置.不同于传统的匿名化模型，差分隐私模型要求数据库中任何一个用户的存在都不应显著地改变任何查询的结果，从而保证了每个用户加入该数据库不会对其隐私造成危险.

近年来，出现了几种基于差分隐私的网格空间分割方法.UG(uniform grid)[6]是利用网格结构划分二维空间数据的早期代表方法，该方法首先对空间数据进行均匀划分，然后再对每个单元格添加相应的拉普拉斯噪音.虽然UG能够比较合理地设定划分粒度，但却没有考虑单元格中计数的稀疏性*稀疏性是指空间中很多0值计数被划分到同一单元格.与偏斜性*偏斜性是指对空间数据分布偏斜方向与程度的度量(参考表1)..例如，图1是从1 000万条纽约出租车数据中抽取到的100万条数据，然后划分成8×8个网格.查询框Q1要求返回该范围内的计数值，其真实的计数为5.这8个单元格所添加的噪音值为8Lap(1ε)，则返回的噪音计数值为5+8Lap(1ε).如果设置ε=0.01，则8Lap(1ε)≈1 000，该噪音值扭曲了真实值5.因此，Q1的查询结果可用性很低.DP-Where(differentially private where)[7]方法同样采用均匀网格对移动人群的位置进行分割，但该方法的不足与UG类似.

为了弥补UG与DP-Where没有兼顾网格单元的稀疏性与稠密性问题，AG(adaptive grid)[6,8]方法采用两层网格结构划分空间数据，该方法对第1层的每个单元格进行自适应地划分，进而可以避免UG与DP-Where的稠密性划分不足问题.虽然AG能够自适应地划分每个网格单元，然而该方法无法顾及用户的查询粒度.例如图1中的Q2查询所覆盖的单元格c9至c12，单元格c9可以继续分割，而c10，c11，c12由于本身的稀疏性无需再继续分割，否则会导致更大的噪音误差.上述3种方法均采用网格结构对空间数据进行分割，然而这些方法存在以下问题.

问题1. UG，AG，DP-Where方法仅仅在小的空间数据上进行了分割，支持相应的范围查询.然而，当数据点达到千万级别时，这些方法的分割与响应查询精度很低.

问题2. UG，AG等方法没有很好地兼顾单元格的稀疏性、稠密性与偏斜性.尽管AG在稀疏性与稠密性作了改进，而该方法没有考虑用户的查询粒度问题，有可能在第2层导致很大的查询误差.

总而言之，目前还没有一个行之有效的方法同时克服上述两种问题带来的不足.为此，本文提出了一种融合抽样与过滤的3层网格分割方法.在满足差分隐私的情况下，采用伯努利抽样技术对大规模原始空间数据进行抽样.在构建网格结构过程中，利用阈值过滤单元格，判断是向下继续分割还是向上合并，进而实现高质量的空间数据分割.

本文主要贡献有4个方面：

1) 为了解决问题1，提出了一种满足差分隐私的抽样方法，该方法利用伯努利抽样技术对海量空间数据进行抽样，该技术不但满足差分隐私需求，而且能够比较精确地抽取原始空间数据.

2) 为了有效解决问题2，提出了3层网格分割方法STAG(sampling-based three-layer adaptive grid decomposition)，该方法利用阈值过滤技术判断第2层中的单元格是否继续分割.对于大于或等于阈值的单元格，采用自适应地向下分割成较细粒度的单元格；对于小于阈值且彼此连接的单元格，则向上重新组成较粗粒度的单元格.

3) 为了比较精确地相应不同粒度的范围查询，本文提出了一种约束推理方法，该方法利用平均化和一致性操作来增强查询结果的精度.

4) 理论分析了STAG方法满足ε-差分隐私，通过真实数据集上的实验分析展示该方法在兼顾高可用性和准确性的同时，优于同类方法.

1 相关工作

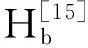
2 定义与问题

相比于传统的隐私保护模型，差分隐私保护模型具有2个显著的特点：1)不依赖于攻击者的背景知识；2)具有严谨的统计学模型，能够提供可量化的隐私保证.

定义1. 设D={d1,d2,…,dn}为原始空间数据点.D′={d1,d2,…,dr-1,dr+1,…,dn}，D与D′相差一个数据点，则二者互为空间近邻关系.

结合D与D′给出ε-差分隐私的形式化定义，如定义2所示：

定义2. 给定一个空间数据分割方法A，Range(A)为A的输出范围，若方法A在D与D′上任意分割结果G(G∈Range(A))满足下列不等式，则A满足ε-差分隐私.

Pr[A(D)=G]≤exp(ε)×Pr[A(D′)=G]，

(1)

其中，ε表示隐私预算，其值越小则算法A的隐私保护程度越高.

从定义2可以看出，ε-差分隐私限制了任意一个记录对算法A输出结果的影响.实现差分隐私保护需要噪音机制的介入，拉普拉斯与指数机制是实现差分隐私的主要技术.而所需要的噪音大小与其响应查询函数f的全局敏感性密切相关.

定义3. 设f为某一个查询，且f:D→d，f的全局敏感性为

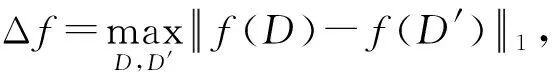
(2)

文献[2]提出的拉普拉斯机制可以取得差分隐私保护效果，该机制利用拉普拉斯分布产生噪音，进而使得发布方法满足ε-差分隐私，如定理1所示.

定理1[2].设f为某个查询函数，且f:D→d，若方法A符合下列等式，则A满足ε-差分隐私.

A(D)=f(D)+Lap(Δfε)n，

(3)

其中，Lap(Δfε)为相互独立的拉普拉斯噪音变量，噪音量大小与Δf成正比、与ε成反比.因此，查询f的全局敏感性越大，所需的噪音越多.

文献[17]提出的指数机制主要处理抽样算法的输出为非数值型的结果.该机制的关键技术是如何设计打分函数u(D,di).设A为指数机制下的某个隐私算法，则算法A在打分函数作用下的输出结果为

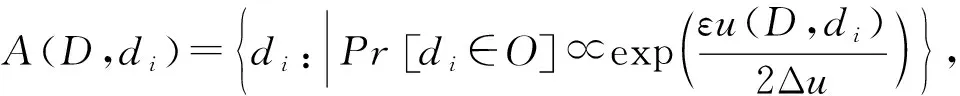
(4)

其中，Δu为打分函数u(D,di)的全局敏感性，O为采用算法的输出域.由式(4)可知，di的打分函数越高，被选择输出的概率越大.

定理2[17]. 对于任意一个指数机制下的算法A，若A满足式(4)，则A满足ε-差分隐私.

3 基于3层网格的自适应空间分割方法

3.1 空间分割的原则

基于相关工作部分的分析，在设计新的基于网格空间分割方法时需要考虑2项原则：

1) 针对大规模空间数据问题，所设计的分割方法应在满足差分隐私条件下尽量能够抽取充足数据点作为分割对象；

2) 针对现有网格分割方法无法有效兼顾用户查询与单元格粒度的缺陷，所设计的分割方法应根据查询框所覆盖单元格的粒度，确定是细粒度分割，还是粗粒度重组.

针对原则1与原则2，本文设计一种基于抽样与过滤的3层自适应网格分割方法STAG.

3.2 STAG算法实现

本节描述STAG算法的具体实现细节.

算法1. STAG算法.

输入：D、隐私预算ε、分割阈值θ；

输出：满足差分隐私的自适应网格结构G.

①V<θ=∅,V≥θ=∅；*V<θ为小于θ单元格 组成的集合，V≥θ为大于或等于θ单元格 组成的集合*

② 以概率γ执行多次伯努利实验，获得样本

Dγ；

③εγ=ln(exp(ε)-1+γ)-lnγ；*由定理3

算出εγ*

④εγ=ε1+ε2+ε3；

⑤ 利用m2×m2网格均匀划分Dγ产生集合Vm2×m2，标注每个单元格ci(ci∈Vm2×m2)为unvisited(ci)=0；*m2为划分粒度，设置ci为未访问单元格*

⑥ whileunvisited(ci)=0 do

⑦V<θ=Threshold-Filter(c(ci),<θ,ε2);

⑧V≥θ=Threshold-Filter(c(ci),≥θ,ε2);

⑨ 标注unvisited(ci)=1；

⑩ end while

算法1包括2个主要步骤：伯努利随机抽样(步骤②③)与网格分割(步骤⑤～).在利用网格对空间数据点进行分割时，如何确定划分粒度m2非常关键，本文基于文献[12]，设定：

其中，|Dγ|表示所抽取的具体样本个数，p2为常数.此外，分割网格存在3种重要操作：利用Threshold-Filter操作过滤第2层中每个单元格，进而形成V<θ与V≥θ集合(步骤⑦⑧).对于V≥θ，调用Down-Split操作向下细分，进而形成自适应网格G的第3层；对于V<θ，调用Up-Merge操作进行重组，进而形成G的第1层.算法STAG的具体思路可由图2给予说明.

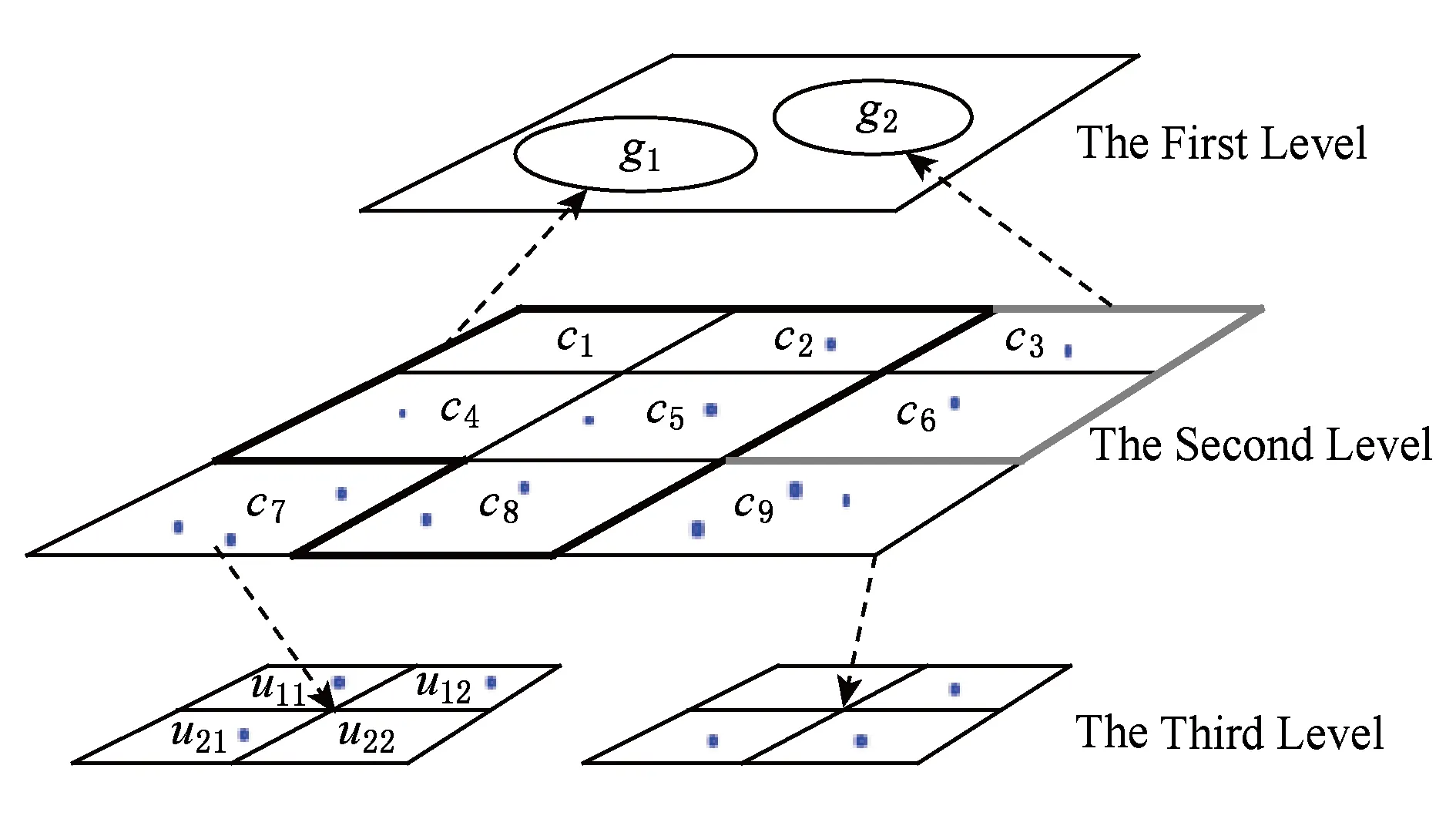
Fig. 2 An example for STAG algorithm图2 STAG算法例子

例如给定Dγ=14个空间数据点，θ=3.在第2层，Dγ被分成3×3的单元格.单元格c7，c9被细分成2×2的单元格，如第3层所示.单元格c1，c2，c4，c5，c8被重组成g1，c3，c6被重组成g2，如第1层所示.

因此，本文的目标是根据范围查询的粒度不同，利用STAG方法生成3层网格来自适应相应查询，并使得查询结果具有较高的精度.接下来介绍如何利用伯努利抽样实现空间分割样本的采集.

3.2.1 伯努利随机抽样过程

STAG算法的第1个重要步骤是伯努利随机抽样，该过程的操作细节如下：

1) 确定抽样概率γ；2)以γ对D做伯努利实验，如果实验成功，则获得空间样本，否则放弃该样本;3)计算出整个空间分割所需的隐私代价εγ(算法1步骤②所示).而该过程的关键在于如何使得抽样过程满足差分隐私.文献[18]给出的定理3说明该过程满足ln(1+γ(exp(ε)-1))-差分隐私.

定理3. 给定一个数据D，令算法A在D上满足ε-差分隐私.如果算法Aγ操作包括：以概率γ从D中抽取样本获得Dγ，然后A作用于Dγ.则Aγ满足ln(1+γ(exp(ε)-1))-差分隐私.

3.2.2 Threshold-Filter阈值过滤

通过阈值θ过滤单元格噪音计数能够提高最终的范围查询精度.然而，θ的选择至关重要，θ过大导致稠密单元格分割不彻底，θ过小导致稀疏单元格重组不够充分.本文利用指数机制与高通滤波设计2种阈值过滤方法.

1) 基于高通滤波的阈值过滤

高通滤波技术是通过经验值确定过滤阈值，例如设置θ=η×lb(|Dγ|ε2)[19].当所需的隐私代价ε2给定后，θ直接有经验值η来确定.本文的高通滤波技术如算法2所示.

算法2. Threshold-Filter-HP算法.

输入：m2×m2个单元格组成的集合Vm2×m2、隐私预算ε2；

输出：V<θ，V≥θ.

①θ=η×lb(|Dγ|ε2)；

② for eachc(ci)(ci∈Vm2×m2) do

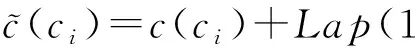
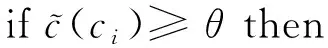
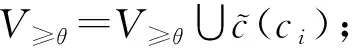
⑥ else

⑧ end if

⑨ end for

⑩ returnV<θ，V≥θ.

算法2针对Vm2×m2中m2×m2个单元格的噪音计数值(步骤③)，采用阈值θ直接过滤，进而生成集合V<θ与V≥θ.尽管算法2可以有效减少网格稀疏和稠密带来的影响，而经验值η的设置却是不易，本文实验中设置η=6.25.

2) 基于指数机制的阈值过滤

利用指数机制在m2×m2个单元格中抽取满足阈值θ的单元格计数关键是设计合适的打分函数.

设Sθ={cj|cj∈Vm2×m2,c(cj)≥θ}.根据Sθ设计相应的打分函数是u(Sθ,c(cj))=max(c(cj)-θ).u(Sθ,c(cj))的敏感度只与c(cj)相关，在原始数据集D中，添加或者删除一个数据点，最多影响Vm2×m2中一个单元格计数，则可以得到Δu(Sθ,c(cj))=1.

算法3. Threshold-Filter-EM算法.

输入：Vm2×m2、常数r、隐私预算ε2；

输出：V<θ，V≥θ.

① 计算Sθ；

② for eachc(cj)(cj∈Sθ) do

③ 计算u(Sθ,c(cj))；

④ 在集合Sθ中无放回地抽取单元格计数c(cj)，且抽取概率满足Pr[c(cj)]∝exp(ε2×u(Sθ,c(cj))4rΔu)；*参数r表示要抽取的单元格个数*

⑤ ifj≤rthen

⑥V≥θ=V≥θ∪c(cj);

⑦ end if

⑧ end for

⑨ for eachc(ci)(ci∈(Vm2×m2-Sθ)) do

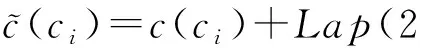
算法3利用指数机制从Vm2×m2抽取r个单元格(步骤②～⑧)，形成集合V≥θ.对剩余(m2×m2-r)个单元格，利用拉普拉斯机制扰动，形成集合V<θ(步骤⑨～).

根据定理1与定理2可知，算法2与算法3均满足ε2-差分隐私.实验部分会对2种过滤方法给详细对比分析.

3.2.3 Up-Merge向上重组过程

该过程是克服单元格稀疏性与提高查询精度的重要技术.对于V<θ中的单元格计数，没有必要采用Down-Split操作向下继续细分，否则细分后会出现更多稀疏单元格.而如何针对V<θ中单元格计数重组粗粒度单元格是个很大挑战.

算法2与算法3中生成的噪音集合V<θ，只是避免在第2层中泄露其真实计数.如果在V<θ直接进行重组，会导致第1层中的查询噪音累加.例如，图2中的g1=c1,c2,c4,c5,c8，若查询Q恰好覆盖g1，则响应结果6+5Lap(1ε2)，进而导致Q的查询精度比较低.因此，本文给出数据依赖的Up-Merge方法.

设V<θ=c(c1),c(c2),…,c(cl)为所有小于θ的单元格真实计数组成的集合.如果直接在V<θ上进行重组，则会破坏差分隐私，因此，利用ε2寻找优化的重组策略.利用ε1对重组后的组平均值添加噪音.

设V<θ被重组成k个分组C=g1,g2,…gk.在重组的过程中，会引入2种误差:1)拉普拉斯机制引起的噪音误差;2)平均值引起的重组误差.设gi=c(cj),…,c(cm)(1≤i≤k,1≤j≤m≤l)为任意一个分组，则|gi|为gi的真实平均值.根据上述分析，可以得到定理4.

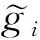
(5)

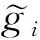
(6)

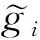
(7)

由|a+b|≤|a|+|b|可知，式(7)满足不等式:

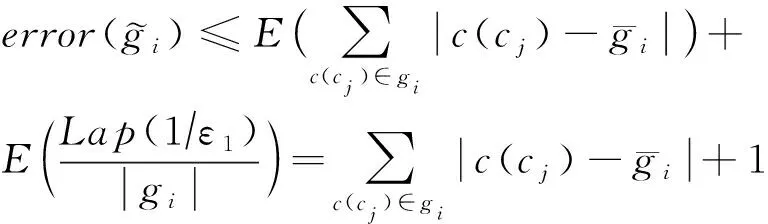
证毕.

根据定理4可以推理出定理5.

定理5. 设V<θ重新分成k个分组后形成C，则C携带的误差满足不等式:

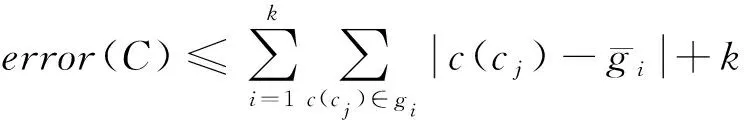
证明. 由定理4可知，定理5成立.

证毕.

根据定理5可知，若使得最终的重组误差最小，重组个数k值的大小至关重要.为了重组方便，设每次重组成k个分组的代价为RC(V<θ,C,ε1)，则RC(V<θ,C,ε1)可以表示成：

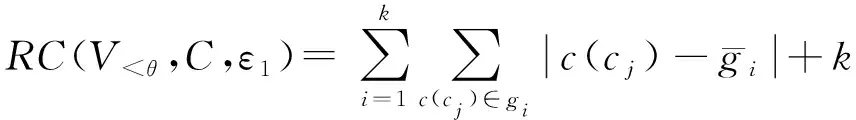
(8)

因此，如何在V<θ中找出一个最优的重组集合C，并使得最小RC(V<θ,C,ε1)，即min(RC(V<θ,C,ε1))，是本文的主要目标之一.

为了避免重组过程破坏差分隐私，利用指数机制与隐私代价ε2来寻找最优化的重组策略.根据式(4)可知，实施指数机制的关键是如何设计打分函数.因此，本文根据式(8)设计打分函数:

(9)

设O为V<θ中所有可能的由k个分组重组的集合.因此，我们希望在集合O中抽取代价较小的一种重组方法.基于上述分析，给出Up-Merge方法的具体实现细节，如算法4所示.

算法4. Up-Merge算法.

输入：V<θ、隐私预算ε1和ε2；

①O=∅；

② for eachk(1≤k≤l) do

③ 计算RC(V<θ,C,ε1)；

④ 生成一种重组形式C，使得O=O∪C；

⑤ 计算u(V<θ,C)=-RC(V<θ,C,ε1)；

⑥ end for

⑦ 以概率

抽取一种重组形式C；

⑧ for eachc(ci) (ci∈C) do

⑩ end for

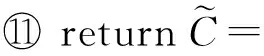
算法4利用指数机制从集合O抽取打分最高的分组C(步骤②～⑦)，然后对C中的每个分组的均值添加拉普拉斯噪音(步骤⑧～⑩).例如图2中，V<θ=c1,c2,c4,c5,c8,c3,c6被重组成g1与g2，2组的噪音计数分别为1.5 +Lap(1ε1)5，1 +Lap(1ε1)2.因此，利用重组结果响应查询所带来的噪音误差较小.

算法4从集合O中抽取C与打分函数有关，但打分函数的敏感度却是控制抽取质量的主要因素.

定理6. 设Δu为u(V<θ,C)敏感度，则Δu≤2.

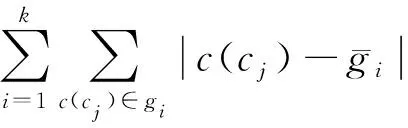
则:

进而获得Δu≤2.

证毕.

由于空间数据本身的稀疏性与偏斜性，使用网格划分时会出现大量计数为0的局部单元格，例如图1Q1查询中的c1,c2,c3,c4单元格计数均为0.这些计数为0的单元格对实际的范围查询没有作用，反而导致Up-Merge操作产生较多的重组误差与噪音误差.如果在第2层所有的单元格中找到那些彼此相连又满足Up-Merge操作的单元格，则能够避免0值的影响.为此，采用图中的连通分量技术，提出了Boost-Up-Merge方法，如算法5所示：

算法5. Boost-Up-Merge算法.

输入：V<θ，V≥θ；

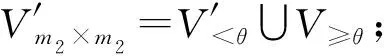
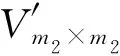
④ for eachcido

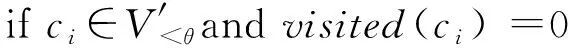
⑥L=L∪ci；

⑦Si=Si∪ci；*Si表示不同的连通分量*

⑧visited(ci) =1；

⑨ end if

⑩ whileL≠∅ do

算法5采用连通分量与凑整(Rounding)技术提高Up-Merge的质量.算法5中的Rounding操作(步骤①)主要考虑大量0值的影响.该操作对V<θ中每个单元格计数过滤，如果原始真实计数为0，则直接把其添加的噪音凑整为0.算法5中步骤④～是计算所有的连通分量Si，针对每个连通分量，利用Up-Merge进行分割重组.例如，图2中第2层为3×3的划分网格，利用Boost-Up-Merge对其操作的结果如图3所示：

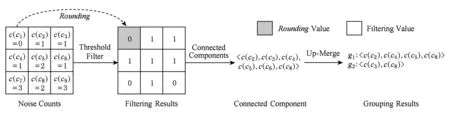
Fig. 3 An example for Boost-Up-Merge algorithm图3 Boost-Up-Merge算法例子

① 假设单元格中数据在均匀分布的情况下响应查询，而数据实际分布与均匀分布存在偏差，该偏差带来的误差为均匀假设误差，参阅文献[6].

图3中Noise Counts表的每个单元格计数通过阈值过滤与凑整操作产生Filtering Results表，其中灰色0是从Noise Counts表中c(c1)的噪音计数经过凑整操作获得的值.Connected Component是经过算法5的步骤④～而获得的连通分量，Grouping Results是调用Up-Merge操作获得的重组结果.

3.2.4 Down-Split向下细分过程

该过程是为了克服单元格过于稠密带来的非均匀假设误差①.对于V≥θ中的单元格，采用Down-Split方法向下细分，进而形成第3层.而向下细分的关键是如何确定第3层划分粒度.

算法6. Down-Split算法.

输入：V≥θ、隐私预算ε3；

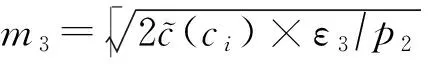
③m3×m3个单元格形成集合Vm3×m3；

④ for eachc(cj) inVm3×m3do

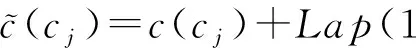
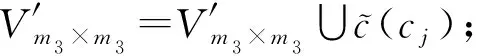
⑦ end for

⑧ end for

算法6首先把V≥θ中的单元格m3根据粒度划分成m3×m3个单元格(步骤②～③);然后对m3×m3个单元格添加相应的拉普拉斯噪音(步骤④～⑦).

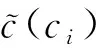
3.2.5 双向约束推理

通过网格的3层自适应分割，可以在每层中获得相应的噪音计数值.为了提高范围查询的精度，基于文献[20]提出了一种约束推理的查询求精方法，该方法的细节如下：

对m3×m3个噪音计数约束推理表达式为

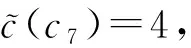
3.2.6 STAG算法隐私性

主要从差分隐私定义角度，证明STAG算法如何满足ε-差分隐私，如定理7所示.

定理7. STAG算法满足ε-差分隐私.

证明. 设A是算法1去掉抽样操作的方法，即是算法1去掉步骤②③.Aγ表示STAG算法本身.首先证明A满足εγ-差分隐私.

A中只有步骤⑦⑧，步骤⑩用到隐私代价.步骤⑦⑧利用阈值过滤形成V<θ与V≥θ集合.利用定理1可知，步骤⑦⑧满足ε2-差分隐私.步骤利用指数机制与拉普拉斯机制重组V<θ，根据定理1与定理2，以及结合差分隐私的并行性质[21]与顺序性质[21]可知，步骤满足(ε1+ε2)-差分隐私.同理结合定理1可知步骤满足ε3-差分隐私.由εγ=ε1+ε2+ε3可知，A满足εγ-差分隐私.

由于εγ=ln(exp(ε)-1+γ)-lnγ，结合定理3可知，算法Aγ满足ln(1+γ(exp(εγ)-1))-差分隐私.把εγ带入ln(1+γ(exp(εγ)-1))，则ln(1+γ(eln(exp(ε)-1+γ)-ln γ-1))=ε.因此，算法Aγ满足ε-差分隐私，由于Aγ表示算法1本身，则STAG满足ε-差分隐私.

证毕.

4 实验结果与分析

实验采用3个数据集NYC①，Beijing②，Checkin③，其中NYC数据集是2011年整个12个月内纽约市出租车的乘车和下车地理坐标数据，该数据集包含1 000万条信息；Beijing数据集是2011年2月份某一周内北京市10 357辆出租车的乘车和下车地理坐标数据，该数据集包含1 500万条信息；Checkin数据集从基于地理位置的社交网站Gowalla获取，该数据集记录了在2009年2月至2010年10月期间，Gowalla用户签到的时间和位置信息，包含6 442 890条记录.3种数据集具体细节与可视化结果分别如表1与图4所示.

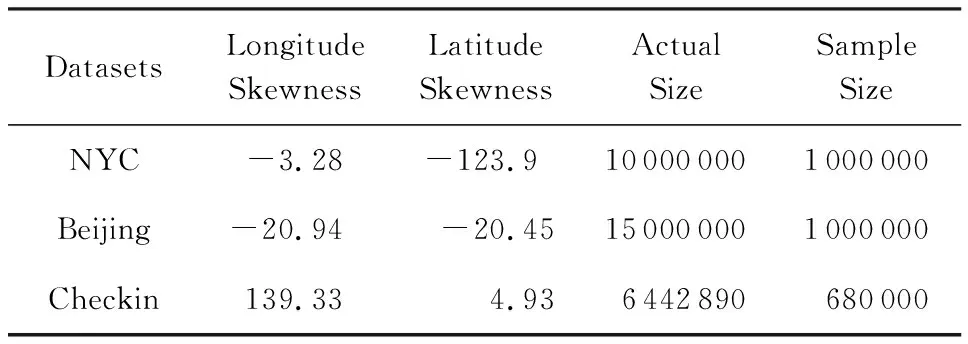
Table 1 Characteristics of Datasets表1 数据集的属性

结合上述3种数据集，类似于文献[6]，采用相对误差(relative error,RE)度量STAG，UG，AG，Kd-Stand，Kd-Hybrid方法的范围查询精度.相对误差如式(10)所示：

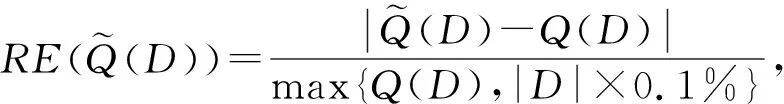
(10)

本文设置伯努利随机抽样概率为10%，隐私预算参数ε的取值为0.1，0.5，1.0.实验中范围查询Q的查询范围分别覆盖NYC，Beijing，Checkin这3种数据集的[1%,5%]，[5%,10%]，[10%,20%]，在每种查询范围内随机生成5 000次查询.本文用到的其他参数设置：θ=40，p2=5，η=6.25.

1) 基于NYC数据集的STAG，UG，AG，Kd-Stand，Kd-Hybrid算法RE值比较

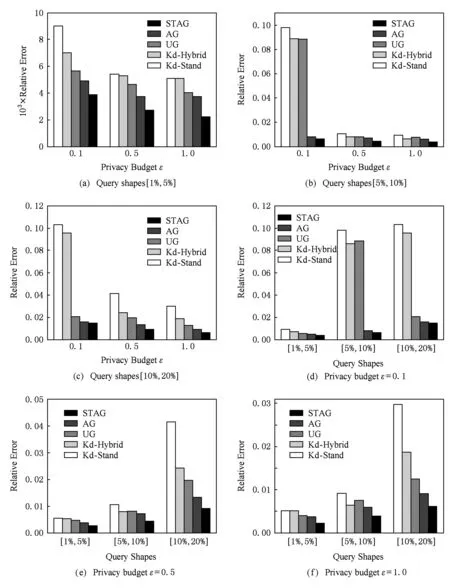
Fig. 5 Results of range queries on NYC dataset图5 NYC数据集范围查询结果

由图5(a)～(c)可以发现，当查询范围固定时，ε从0.1变化到1.0，5种方法的RE均减少.然而，STAG的范围查询精度明显优于其他4种方法.在ε=1.0时，STAG所取得的查询精度是AG与UG的将近2倍，是Kd-Stand与Kd-Hybrid的将近3倍.特别在查询范围是[5%,10%]且ε=0.1时，STAG所取得的查询精度是UG，Kd-Stand，Kd-Hybrid的将近10倍.图5(d)～(f)显示，查询范围从[1%,5%]变化到[10%,20%]且ε固定时，STAG同样优于其他4种方法.当ε=0.1且查询范围为[5%,10%]时，STAG所取得的查询精度是UG，Kd-Stand，Kd-Hybrid方法的将近9倍.其原因是NYC数据集的偏斜度比较严重(由表1可知，经纬度偏斜值为-3.28-123.9)，而STAG利用抽样与3层自适应网格能够较好地避免偏斜与稀疏问题.

2) 基于Beijing数据集的STAG，UG，AG，Kd-Stand，Kd-Hybrid算法RE值比较

由图6(a)～(c)可以看出，固定查询范围且变化ε时，STAG的查询精度优于其他4种方法.查询范围为[1%,5%]时，STAG的查询精度优于其他4种方法不到1倍.而随着查询范围扩大，STAG的查询精度优势比较明显.特别是查询范围为[10%,20%]且ε=1.0时，STAG所取得的查询精度是Kd-Stand与Kd-Hybrid的将近5倍，是UG的将近3倍.由图6(d)～(f)显示，查询范围从[1%,5%]变化到[10%,20%]且ε固定时，STAG所取得的查询精度与AG差别不是很大，然而却优于剩余3种方法.特别是在ε=1.0时，STAG取得的查询精度是UG与Kd-Hybrid的将近3倍，是Kd-Stand的将近6倍.

Fig. 6 Results of range queries on Beijing dataset图6 Beijing数据集范围查询结果

3) 基于Checkin数据集的STAG，UG，AG，KD-Stand，KD-Hybrid算法RE值比较

图7(a)～(c)显示，变化ε且固定查询范围时，STAG的查询精度明显优于其他4种方法，是AG与UG的将近2倍，是Kd-Hybrid的将近3倍.特别在ε=0.1且查询范围为[10%,20%]时，STAG所取得的精度是Kd-Stand的3倍之多.图7(d)～(f)显示，变化查询范围且固定ε时，STAG所取得的查询精度同样好于其他4种方法，其查询精度是AG，UG，Kd-Hybrid的将近2倍，是Kd-Stand的将近11倍.其原因是Checkin数据的稀疏性很高(经纬度偏斜值为139.334.93)，STAG利用抽样、过滤以及向上重组技术避免了Checkin数据的稀疏性与偏斜性.

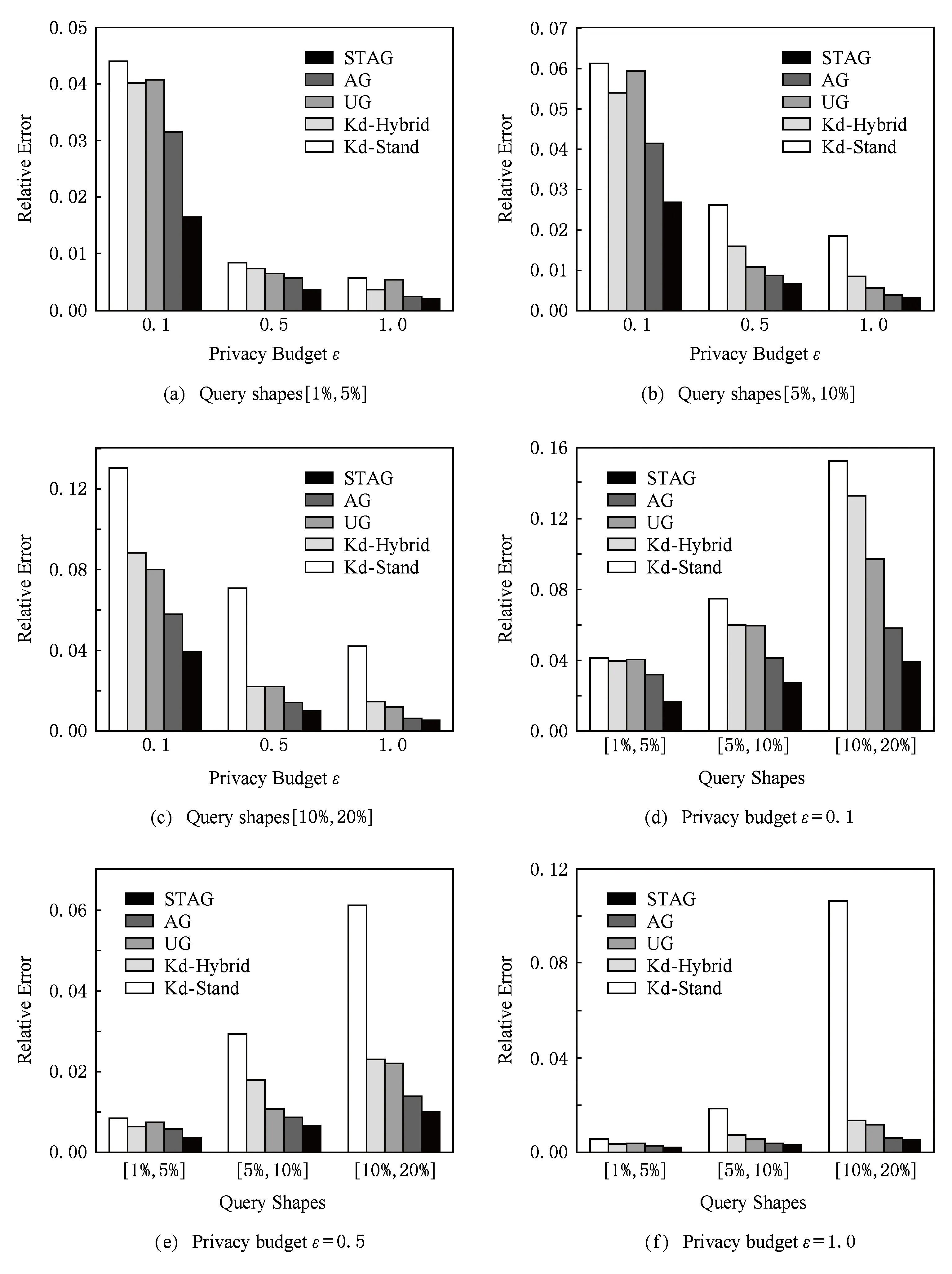
Fig. 7 Results of range queries on Checkin dataset图7 Checkin数据集范围查询结果

4) 基于3种数据集的阈值过滤方法对比分析

本文2种阈值过滤技术主要受到参数η与r的影响.设置ε=0.5，查询范围为[5%,10%].图8(a)～(c)显示了η与r变化对范围查询相对误差的影响.从图8(a)～(c)可以看出，参数r从70%变化到90%时，3种数据集上的查询误差均在η=6.25时达到最小,此时对应的阈值θ=40.参数η从3.91变化到7.03时，参数r在Checkin数据上，值为80%时查询误差到达最小.而在NYC与Beijing 数据上，值为75%或者80%时，查询误差达到最小.因此参数η与r的设置直接制约着最终阈值过滤的效果.

6 结束语

针对差分隐私保护下基于网格空间分割存在的问题，本文结合现有的网格分割方法存在的不足，提出了基于伯努利随机抽样的3层网格分割方法.该方法通过向下细分与向上重组操作来提高空间范围查询精度，从差分隐私定义角度分析STAG满足ε-差分隐私，最后通过3种真实的大规模数据集验证了STAG方法的范围查询精度.实验结果表明，STAG明显优于现有的同类方法.未来工作考虑动态环境下的隐私空间数据分割问题.

[1]Sweeney L. K-anonymity: A model for protecting privacy[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(5): 557-570

[2]Dwork C, McSherry F, Nissim K, et al. Calibrating noise to sensitivity in private data analysis[C]Proc of the 3rd Theory of Cryptography Conf (TCC 2006). Berlin: Springer, 2006: 363-385

[3]Dwork C. Differential privacy[C]Proc of the 33rd Int Colloquium on Automata, Languages and Programming (ICALP 2009). Berlin: Springer, 2006: 1-12

[4]Dwork C, Lei J. Differential privacy and robust statistics[C]Proc of the 41st Annual ACM Symp on Theory of Computing (STOC 2009). New York: ACM, 2009: 371-380

[5]Montjoye D, Hidalgo Y A. Unique in the crowd: The privacy bounds of human mobility[J]. Nature: Scientific Reports, 2013 (3): 1376-1376

[6]Qardaji W H, Yang W, Li N. Differentially private grids for geospatial data[C]Proc of the 29th IEEE Int Conf on Data Engineering (ICDE 2013). Piscataway, NJ: IEEE, 2013: 32-33

[7]Mir D J, Isaacman S, Caceres R, et al. DP-Where: Differentially private modeling of human mobility[C]Proc of the 2013 IEEE Int Conf on Big Data (BigData 2013). Piscataway, NJ: IEEE, 2013: 580-588

[8]To H, Ghinita G, Shahabi C. A framework for protecting worker location privacy in spatial crowdsourcing[J]. Proceedings of the VLDB Endowment, 2014, 10(7): 919-930

[9]Xu Jia, Zhang Zhenjie, Xiao Xiaokui, et al. Differential private histogram publication[J]. International Journal of Very Large Database, 2013, 22(6): 797-822

[10]Michael H, Ashwin M, Gerome M. Principled evaluation of differentially private algorithms using DPBench[C]Proc of the 2016 ACM SIGMOD Int Conf on Management of Data (ACM SIGMOD 2016). New York: ACM, 2016: 139-154

[11]Su Sen, Tang Peng, Cheng Xiang, et al. Differentially private multi-party high-dimensional data publishing[C]Proc of the 32nd IEEE Int Conf on Data Engineering (ICDE 2016). Piscataway, NJ: IEEE, 2016: 205-216

[12]Xiao Yonghui, Xiong Li, Yuan Chun. Differentially private data release through multidimensional partitioning[C]Proc of the 7th VLDB Workshop on Secure Data Management (SDM 2010). Berlin: Springer, 2010: 150-168

[13]Cormode G, Procopiuc C M, Srivastava D, et al. Differentially private spatial decompositions[C]Proc of the 28th IEEE Int Conf on Data Engineering (ICDE 2012). Piscataway, NJ: IEEE, 2012: 20-31

[14]Zhang Jun, Xiao Xiaokui, Xie Xing, et al. PrivTree: A differentially private algorithm for hierarchical decomposi-tions[C]Proc of the 2016 ACM SIGMOD Int Conf on Management of Data (ACM SIGMOD 2016). New York: ACM, 2016: 155-170

[15]Qardaji W H, Yang Weining, Li Ninghui. Understanding hierarchical methods for differentially private histograms[J]. Proceedings of the VLDB Endowment, 2013, 6(14): 1954-1965

[16]Kellaris G, Papadopoulos S. Practical differential privacy via grouping and smoothing[J]. Proceedings of the VLDB Endowment, 2013, 6(5): 301-312

[17]McSherry F, Talwar K. Mechanism design via differential privacy[C]Proc of the 48th Annual IEEE Symp on Foundations of Computer Science (FOCS 2007). Piscataway, NJ: IEEE, 2007: 94-103

[18]Li Ninghui, Qardaji W H, Su Dong. On sampling, anonymization, and differential privacy or,k-anonymization meets differential privacy[C]Proc of the 7th ACM Symp on Information, Computer and Communications Security (AsiaCCS 2012). New York: ACM, 2009: 32-33

[19]Michael H, Vibhor R, Gerome M. Boosting the accuracy of differentially private histograms through consistency[J]. Proceedings of the VLDB Endowment, 2010, 3(1): 1021-1032

[20]Lei Jing. Differentially privatem-estimators[C]Proc of the 25th Annual Conf on Neural Information Processing Systems (NIPS 2011). Berlin: Springer, 2011: 361-369

[21]McSherry F. Privacy integrated queries: An extensible platform for privacy-preserving data analysis[C]Proc of the 2009 ACM SIGMOD Int Conf on Management of Data (ACM SIGMOD 2009). New York: ACM, 2009: 19-30

ZhangXiaojian, born in 1980. PhD, associate professor in the School of Computer and Information Engineering, Henan University of Economics and Law. His main research interests include differential privacy, data mining, and graph data management.

JinKaizhong, born in 1991. MSc candidate in the School of Computer and Information Engineering, Henan University of Economics and Law. His main research interests include differential privacy, database, etc.

MengXiaofeng, born in 1964. Professor and PhD supervisor at Renmin University of China. Executive director of CCF. His main research interests include cloud data management, Web data management, native XML databases, flash-based databases, privacy-preserving, and etc.