基于信任的云服务系统多目标任务分配模型
2018-06-08梁昌勇
束 柬 梁昌勇 徐 健
(合肥工业大学管理学院 合肥 230009) (优化与智能决策教育部重点实验室(合肥工业大学) 合肥 230009) (shujian7@163.com)
在全球经济一体化进程迅速发展的背景下,企业面临着外部资源和环境压力持续加大,内部也面临着产品和服务创新乏力、资源消耗大等难题.云计算等新兴信息技术和面向服务的体系框架为企业提高生产经营效率,从更大范围内整合资源和协同价值创新,建立更加高效低碳的运营体系和服务模式等提供了契机.然而,新的云服务模式在重新整合产业链和协同价值链的过程中也带来了新的安全隐患,虚拟化的远程服务模式和多主体的协同服务特征等不断拓宽以往传统的信息安全边界,带来了更多的安全风险.传统信息安全技术无法很好地解决该问题,基于信任的系统管理方法为其提供了全新的思路
云计算为企业提供的服务主要有3种模式:软件及服务(software as a service, SaaS)、平台即服务(platform as a service, PaaS)以及基础设置即服务(infrastructure as a service, IaaS)[1].此外,集合企业自身系统架构,云服务也分为由企业内部信息资源虚拟化而成的私有云服务、外部云服务商提供的公有云服务,及两者皆有的混合云服务[2].针对云服务模式已有较为广泛的研究:Dorsch等人[3]从盈余能力的经济影响角度讨论了云服务能力,以云服务弹性的容量供应策略应对不稳定需求.Boru等人[4]以建立了一种数据复制方法解决云服务数据中心存储海量数据的节能问题.罗军舟等人[5]将云服务划分为核心服务、服务管理、用户访问接口3层体系架构,总结了云服务的关键技术和热点问题.李乔等人[6]从云服务类型和框架层次的角度综述了不同的云计算服务.
基于云的管理系统的服务对象是包含企业生产经营等一系列活动的业务流程.业务流程对于企业而言如同经脉对于人体,是形成信息流动和资源交换的重要载体.单个业务流程可被划分为很多个彼此存在限制关系的任务单元[7],如何分配和调度该类任务单元以保障整个业务流程的顺利完成是并行系统的热点问题[8-9].Liu等人[10]引入流矩阵以表示待分配任务节点间约束的关系的权重.Topcuouglu等人[11]建立异构计算环境下动态高效低复杂性的任务调度算法.Wen等人[12]采用GA算法结合邻域搜索,建立了异构多进程系统中的启发式的任务调度算法.而现有研究对任务结构的总结多限于并行或串行结构,缺乏多样性,本文引入6种典型任务结构到任务分配模型中,以增强模型真实性和可用性.
云计算服务在带来高效便捷的同时,其跨组织的分布式服务模式也必将带来新的安全问题[13].考虑不同任务对服务资源具有不同的信任安全需求,如涉及商业机密数据的任务有更高的安全需求,而服务资源根据其服务声誉和服务模式的差异也具备不同的可信度.在信息系统领域中,对信任机制的相关理论和关键技术的研究日趋成熟[14-15].Krautheim等人[16]在云环境中构建了基于加密算法和可配置模块化架构的可信虚拟环境模块(TVEM).Manuel[17]将信任引入服务质量(QoS)参数中,以可用性、可靠性、周转效率和数据完整性4个参数来计算服务的信任值.李勇军等人[18]讨论了信任机制与网络安全的相关性,在信任机制的研究框架下总结了典型信任模型.徐锋等人[19]给出了考虑凭证的存储及授权形的信任链发现算法,防止有效敏感信息的泄露.可以看出,信任机制为解决云计算的分布式和远程服务等技术特征带来的新安全问题,提供了很好的理论依据和技术方法[20].故本文在定义了云环境中信任关系的基础上,结合前期研究成果[21],将信任机制引入模型中,在时间和成本目标的基础上添加信任约束和信任目标,在保障云服务系统拓展性的同时兼顾安全可信性.
本文的主要贡献有4个方面:
1) 结合面向服务框架(SOA),构建了混合云环境下业务流程驱动的云服务系统体系架构,并引入信任机制以量化云服务中资源的可信程度和待执行任务的信任需求;
2) 在该架构基础上建立了业务流程驱动的多目标任务分配模型,引入运行时间、成本和信任3个目标,在保障系统高效率低成本的同时兼顾安全可信性;
3) 从业务流程层面构建了任务结构函数范式,梳理和总结了6种典型任务结构的多目标函数关系式;
4) 提出了基于局部搜索策略的改进SPGA2(strength Pareto genetic algorithm 2)算法,在结合SPEA2和GA算法的基础上,引入基于双点小步距跃进的局部搜索策略以提高搜索效率,通过仿真实验验证了算法的有效性.
1 系统架构与优化模型
1.1 基于混合云的可信服务系统体系架构
本文在企业原有系统基础上,结合企业内部原有可信服务资源和外部云服务商提供的云服务资源,对企业服务系统进行再造升级,构建了基于混合云的综合服务信息系统,其系统框架如图1所示.该框架从企业服务需求端和提供端2个方面出发,将综合服务系统剖析为4个逻辑层:任务层、调度层、虚拟服务层和平台及基础设施层,并对综合服务系统中的关键技术和基础要素进行详细分析和总结.
任务是从企业析出的业务流程分解而产生的一系列可通过服务满足其需求的子单元.从需求角度来看,企业用户将其所需服务的流程提交到系统中,通过流程控制器首先将接收到的流程及其基本信息进行提交注册,然后将各流程分解为独立的可执行任务单元,例如,一项电子商务流程可分解为以下任务单元:订单采集、验证、核实、购物车管理和支付单元等.随后控制器将这些可执行的任务单元提交到任务管理器中,通过任务管理器实现对所有任务单元的统一管理.任务管理器的重要功能为对任务单元属性特征的解析和记录,任务单元的主要属性包括:任务量、执行优先级和信任需求等.任务量是指任务运行完成所需要的服务资源的大小;任务优先级是为了保障业务流程内部秩序和避免死循环而设立的任务间先后执行关系;信任度需求是不同任务对服务资源可信度的需求情况表征.从服务资源的提供角度来看,企业将其内部IT资源整合私有云服务资源,并接入外部公有云服务资源.公有云资源分为2类:1)租用IaaS基础设施服务,在其上部署自己的平台和应用服务;2)直接租用PaaS平台服务,并在其上部署应用服务.外部的公有云服务都是通过服务收集器进行服务注册和服务监控的,通过服务等级协议(SLA)来保障服务质量(QoS).通过资源管理中心,将公有云资源和私有云资源抽象成具有固定属性的服务单元,并将其信息发布到调度层的资源池中,以待分配任务.且本模型假设一个资源槽在同一时间只能运行一个任务,不同服务资源槽具有其独立的属性.服务单元的主要属性有服务能力、单位时间成本、资源可信度.从服务资源的属性上来看,私有云资源拥有更高的可信度,服务能力更强,但需要更高的成本;公有云虽面临一定信任风险,但是成本低廉,可选择范围更广.
1.2 云服务中的信任机制
信任值的引入是保障整个服务系统在任务分配和服务选择过程中兼顾节能高效和安全可靠.模型定义不同任务单元有不同的信任需求RTn,而云服务资源的可信度STm由该资源的综合信任值所决定.云服务资源的综合信任值是由服务用户对资源的直接信任值和云商间的推荐信任值融合而得,其融合方法参考前期研究成果[21]所示.推荐信任值取决于云商之间交互的历史信息,此处不再赘述.而本文重新详细定义了用户对云服务资源的直接信任值:直接信任值取决于云服务资源的服务模式和供应商声誉.从云服务模式角度,用户对系统平台或基础设施所拥有的控制权限越高,则该服务资源的直接信任值就越高.如用户使用企业内部私有云部署的软件服务资源可信度较高;而若用户直接租用SaaS类服务资源,其对底层系统或基础设施没有所有权,则该类资源的可信度就较低.需要说明的是,可信度的高低只是代表概率上的潜在的风险,并不代表资源的服务能力和状态.从云服务供应商声誉角度,若供应商有着良好的声誉口碑和优质的服务能力,其必然是一个高可信度的供应商;若其在声誉上有瑕疵或者在历史记录中有过服务不达标的记录,客户就会降低其可信度.本模型将信任需求和资源可信度分为7级,如表1所示:
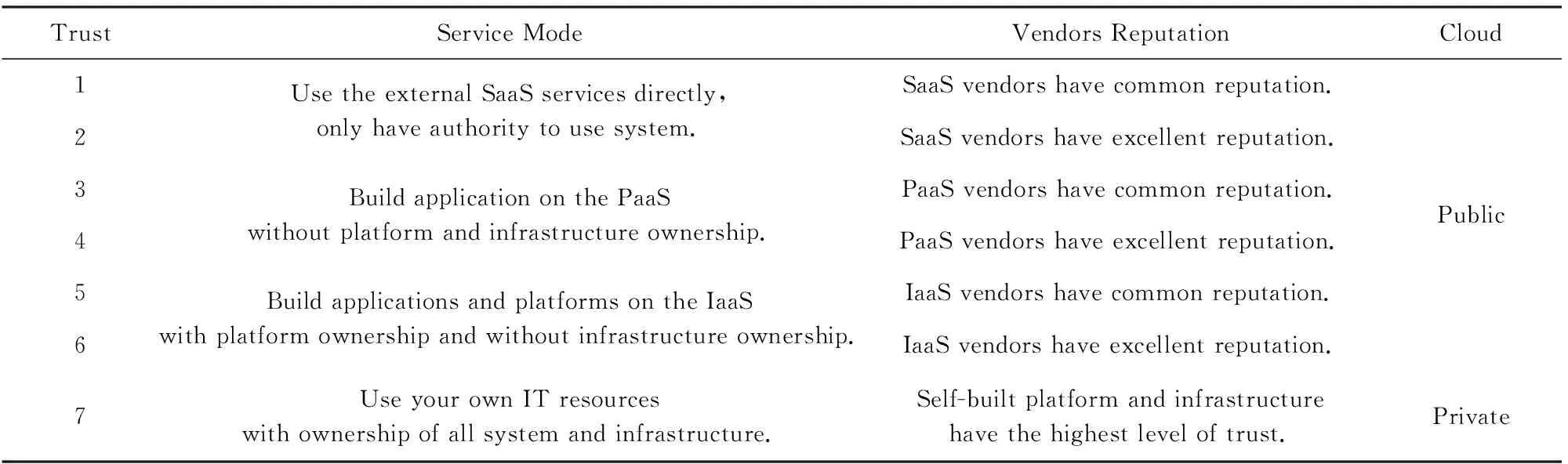
Table 1 The Classification of Trust表1 信任等级分类
在混合云环境下,由本地基础设施提供的私有云服务被定义成为高可信度7;而公有云服务根据资源类型、供应商声誉和云商间推荐信任值等将其可信度分为1~6级.本文将信任机制引入多目标优化问题中,在时间和成本目标维度外加入了信任维度.
1.3 基于时间、成本和信任的多目标任务分配模型
企业的某项业务流程BP可分解为N个任务单元{T1,T2,…,TN},并假设共有M个服务单元{S1,S2,…,SM}接入企业的服务系统中.该多目标优化问题可以看成:企业如何分配N个任务到M个服务单元中,使得任务执行时间最短、执行成本最低、信任度最高.本节总结了单个任务的多目标函数关系式,而对整个业务流程而言,其考虑任务结构的多目标函数关系将于第2节详细讨论.
对于运行在不同的服务单元中的任务单元来说,其执行时间主要取决于任务的资源需求量和资源的服务能力scm,故任务tn在服务资源Sm上的运行时间可表示为
D(tn)=Unscm.
(1)
模型假设云服务按使用时长收费,不同云服务资源有相应的单位时间成本.考虑私有云服务前期固定设备投入、场地费用、系统维护和专业人员薪酬等,故设定私有云服务的单位成本高于公有云.任务的执行成本C(tn)取决于其运行时D(tn)和服务资源的单位时间成本costm,故可得:
C(tn)=D(tn)×costm=Unscm×costm.
(2)
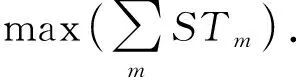
RTn≥STm.
(3)
综上所述,可信混合云服务系统中的任务分配问题可以总结为一个多目标优化问题,其目标空间包括任务运行时间、运行成本和信任值3个维度.同时,将信任限制和任务结构等引入约束条件.该多目标优化问题具体表征为
minFX[D(t1),D(t2),…,D(tx)],
(4)
minFX[C(t1),C(t2),…,C(tx)],
(5)
maxFX[ST(t1),ST(t2),…,ST(tx)],
(6)
s.t. {t1,t2,…,tx}⊆BPa,
(7)
RTx≥STy,
(8)
FX⊆[Fseq,Fand,For,Fxor,Fsl,Fcl],
(9)
其中,式(4)~(6)为目标空间,式(7)表明所有任务属于某个流程,式(8)为信任约束,式(9)是根据任务结构确定的函数关系式.
2 业务流程驱动的多目标任务结构范式
在企业日常经营活动中,提交到系统中待执行任务不是彼此割裂的孤立单元,而是涉及不同优先级结构化的任务单元组合.而这些任务组合形成不同的业务单元,本文梳理了6种业务流程的基本组成单元,建立业务流程驱动的任务结构函数范式.选用行业标准建模语言——业务流程建模符号(BPMN)[22]建立6种典型任务结构:序列、并行-且、并行-或、并行-异或、循环-简单、循环-组合.其中对异或和循环结构通过引入概率分布并计算期望的形式总结其目标函数关系式.不同业务单元对目标的函数范式如表2所示:
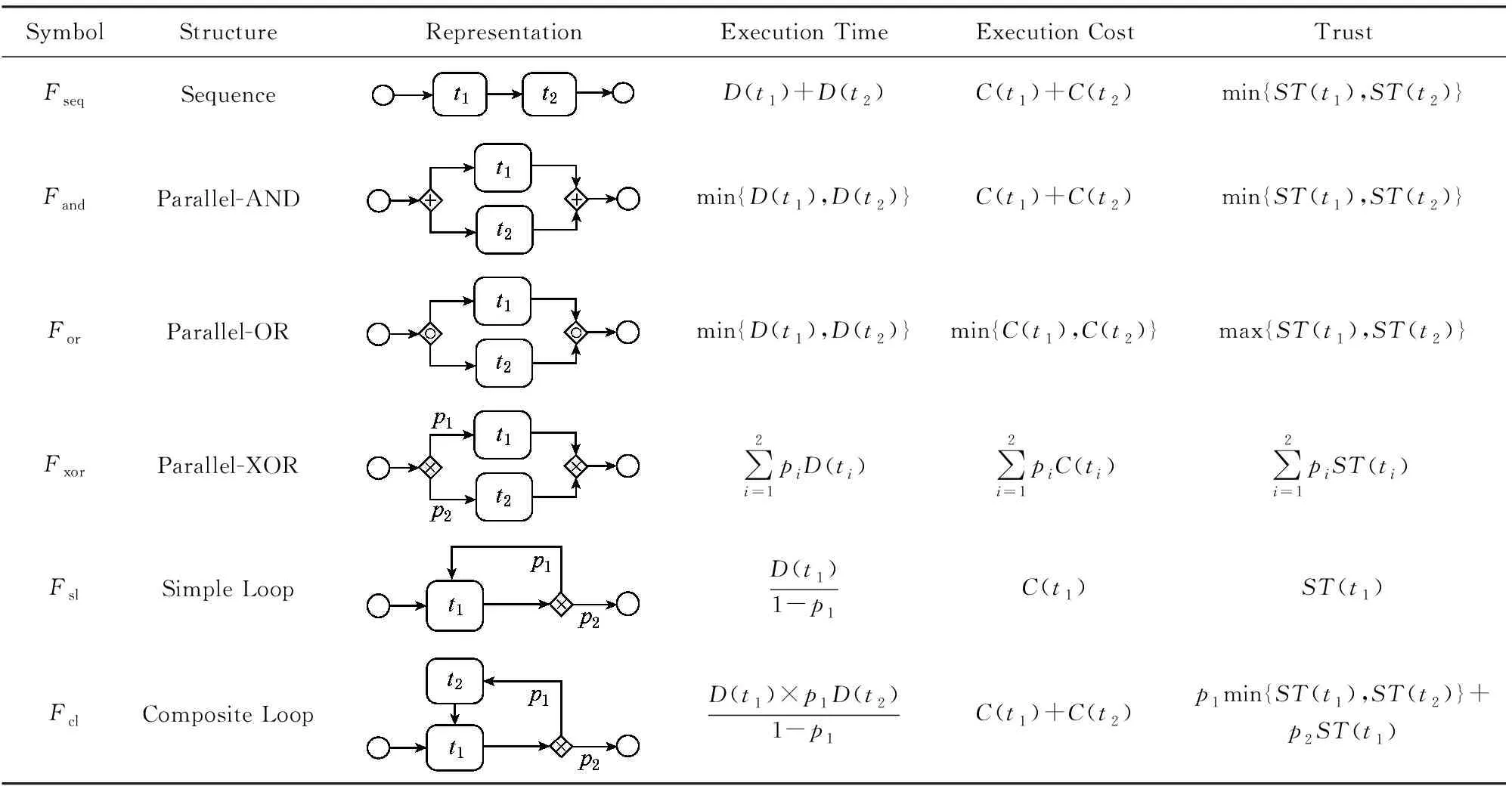
Table 2 Multi-Objectives Functions of Business Process Driven Task Structure表2 业务流程驱动的多目标任务结构函数关系式
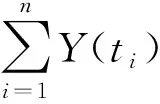
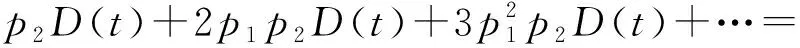
(10)
而在组合循环结构中时间函数为
(11)
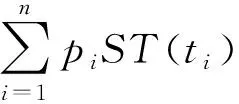
Fcl[ST(t1),ST(t2)]=
p1Fseq[ST(t1,t2)]+p2Fseq[ST(t1)]=
p1min{ST(t1),ST(t2)}+p2ST(t1).
(12)
3 改进SPGA2的多目标任务分配算法
针对混合云中业务流程驱动的多目标任务分配问题,本文提出了一个改进的SPGA2算法,其结合SPEA(strength Pareto evolutionary algorithm)算法和传统GA算法的基础上,引入了双点小步距定向探寻的局部搜索策略,在保证算法全局搜索效率的同时,也提高其局部收敛性.其基本流程如图2所示:
3.1 SPEA2算子
算法执行首先需要通过编码过程将任务空间和资源空间的分配策略映射到抽象的解空间上去,以数字编码形式表示不同的分配策略.随后执行初始化流程,随机生成一个空间大小为NP的初始种群P和一个大小为Nq的外部存档集Q,并令Q=∅.SPEA2采用更详细的适应度分配策略,同时考虑了其中个体的支配信息和被支配信息[23].支配信息由个体的强度值获得,被支配信息由个体的准适应度r(i)获得,再结合密度d(i)最终生成适应度f(i):
f(i)=r(i)+d(i),
(13)
其中各部分的组成为
S(i)=|{j|j∈P+Q∧i≻j}|,
(14)
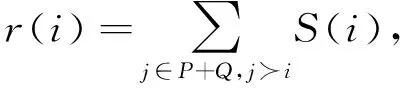
(15)
d(i)=1
(16)
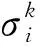
环境选择过程是SPEA2中从群体P中生成新一代存档集Q的重要步骤.其主要过程首先复制所有适应度低于1的非支配个体,并放入外部存档集中:
Qt+1={i|i∈P+Q∧F(i)<1}.
(17)
当所有适应度小于1的个体都放入外部存档集后,比较存档集中的个体数|Qt+1|与规定的规模Nq.若|Qt+1|
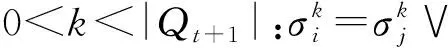
(18)
其实质为依次删除归档集中与个体i距离最近的个体,直至|Qt+1|=Nq.
3.2 局部搜索策略
SPEA和GA算法都具备很强的全局搜索能力,尤其针对有连续光滑边界的多目标优化问题具备很强的收敛能力.而当最优边界不连续、不光滑时,割裂的最优边界严重制约该类算法的收敛能力.原因在于进化算法为了防止寻优过程陷入局部收敛而扩大随机搜索范围的过程中,往往会忽略局部优化问题,导致算法在搜索过程中直接跳过局部的最优边界,跳到下一个最优点.为此,本文引入局部搜索策略,对历代存档集中的非支配个体进行邻域搜索,以在原有非支配集合的基础上获得更优秀的个体,逐步逼近最优边界.计算过程如算法1所示.
算法1. 双点小步距跃进的局部搜索策略.
输入:归档集Q、本地搜索概率p;
输出:新的存档集Q′.
① 通过p搜索Q中个体并存本地集local_pop;
② foriinlocal_pop
③ forpoint1 ini
④point2←i[random(0,len(i))];
⑤point1+=1,point2+=1;
⑥ iftrust(point1)==False
⑦point1-=1;
⑧ end if
⑨ iftrust(point2)==False
⑩point2-=1;
本文采用双点小步距跃进的局部搜索策略,在历代存档集中以概率p选择出非支配个体,采用小步距定向搜索的方式扩展搜寻其周围空间.双点小步距跃进是选择个体中染色体2个点的编码信息进行增位变动,即对1次任务分配方案中的2个任务单元所分配的资源序号进行增加1位操作,需要注意的是若单点的变化过程中破坏了信任约束则不执行增位变动.
3.3 遗传算子
在获得经局部优化的新存档集后,合并新存档集Q′和群体P,并对其进行一系列GA操作以获得新的子代.本文选用传统GA的选择,交叉和变异操作实现解空间的全局寻优.采用轮盘赌选择法选出个体进行交叉变异操作,遗传算子的基本流程如算法2所示.
算法2. 轮盘赌选择法和交叉变异操作主要流程.
输入:种群population、资源集合R;
输出:新种群new_pop.
①score←total_fitness×random(0,1);
② foriinpopulation
③sum_fitness+=fitness(i);
④ ifsum_fitness≥score
⑤s1←i;
⑥ end if
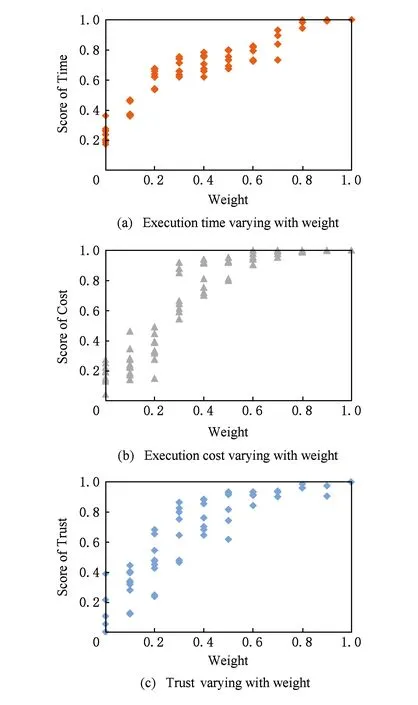
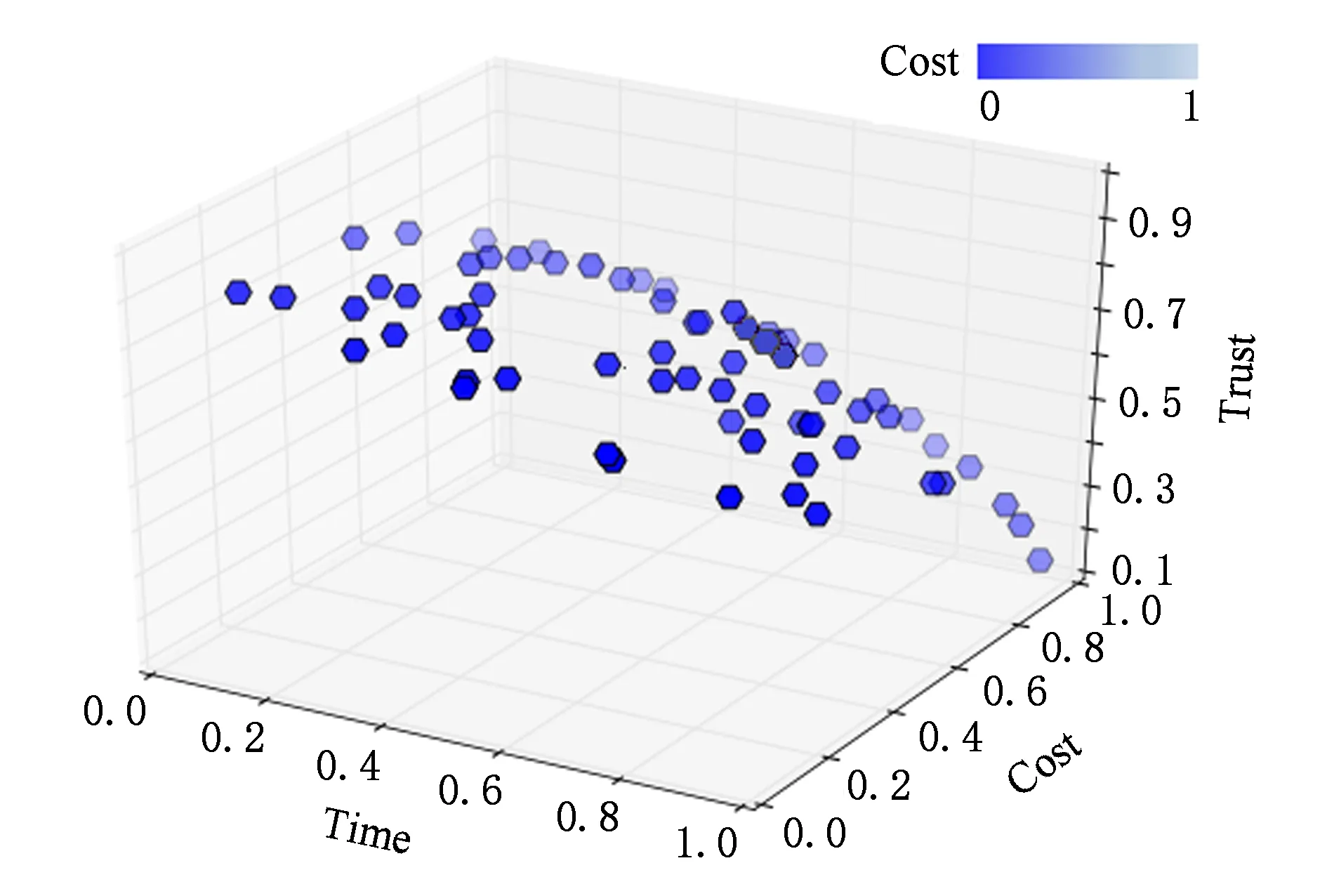
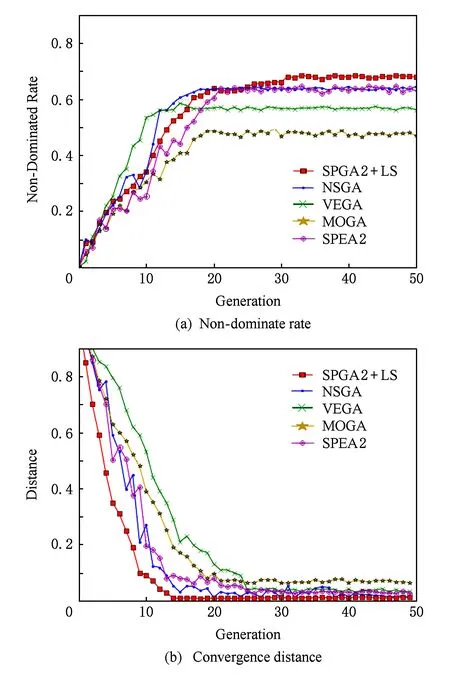
⑦ ifrandom(0,1) ⑧p←random(0,max(s1)); ⑨ end if ⑩ 在population中随机找s2; s2[p:]; 交叉操作通过算法寻优过程中生成新子代的同时保留父代的一些结构特征.采用随机单点交叉算法,随机生成交叉点并保留其左端基因段,交换其右侧基因段以形成2个后代.变异操作是通过改变1个染色体中的某段基因来扩大算法的搜索空间以防止算法过早收敛.模型同样选用随机点变异方法,通过随机函数选择染色体上任意位置的基因片段,再随机生成1个新的基因片段.本模型采用交叉率和突变率表示算法中执行交叉操作或变异操作的概率.需要注意的是,交叉操作是交换现有子代中的基因,而现有子代中基因所携带的信息都是符合信任约束的,故交叉操作不会打破任务分配中的信任信息.而变异操作是非定向的随机搜索过程,其可能破坏原有的信任规则,产生携带不可信调度信息的基因片段,故本文在变异操作中增加了信任约束,不符合信任约束的突变基因将不会替代原基因,算法将重复随机生成满足信任约束的基因片段为止. 为了验证混合云环境下基于信任的动态任务分配模型和算法性能,本文编程实现了一系列仿真实验,并对实验数据和结果进行了详细的梳理分析和总结.实验平台搭建在一台Intel Core 2 Duo-E8400@3.00 GHz CPU和4 GB RAM的PC上,操作系统为Windows Enterprise版本,采用Python 3.5.2编程实现其相应功能,用面向对象的编程语言设置任务单元和服务资源单元,并赋予相应的特征和属性值.本文将实验中数据都进行规范化处理,即采取从0到其极值点转化为0-1标准化形式,以便数据间的比较和分析. 本文首先采用单目标权重分配方法对模型中3个目标函数进行独立分析.实验对象选取包含24个任务的复杂业务流程和8个不同属性的服务资源.通过将各目标权重从0~1以0.1为步长进行历遍,共产生66种不同的权重组合.相应目标权重下目标函数值的得分情况如图3所示: Fig. 3 Variation of single objective with weight图3 单目标随权重变化情况 从图3分析可得:单个目标在获得高目标值的情况下并不意味着会遏制其他目标值得分,如成本目标和信任目标在0.3的权重分配中就可得到接近0.9的得分.该结果揭示了该任务分配问题中多个目标间并非完全冲突,可以找到在3个目标值上都有较好得分的优秀解.故启发式算法对该类问题有很好的处理能力,其验证了算法的可行性.此外,当决策者不考虑全局因素,侧重单目标分析信息,这些解的分布情况提供了重要参考. 在模型和算法可行性的基础上,通过仿真实验实现了改进的SPGA2算法,并用于到多目标任务分配的模型上.建立了一个三维立体散点图,从全局视角展示了算法所得的最终解集,三维视图的X轴、Y轴和Z轴分别表示时间、成本和信任3个目标维度,采用标准化取0-1为单位范围.为了便于比较,取进化算法的种群数量也为66,故生成的66个解展示如图4所示: Fig. 4 Non-dominated solutions by the proposed algorithm图4 多目标任务分配算法所得非支配解 通过图4中点的分布,可看出其形成了一个多目标优化问题的帕列托边界,该边界上的所有解都是非支配的,即对一个非支配解无法找到更好的解在3个目标上都优于该解.在实际生产中,需要根据管理者的偏好和具体环境的限制约束,在所有非支配解中选出最适合的解作为任务分配问题的最优解方案.如追求低成本的公司可能更多侧重成本目标,而对任务内容保密性要求较高的企业可能对成本并不敏感,更侧重于信任目标. 为了更好地展现算法性能,本节选取4个经典多目标优化算法(NSGA,VEGA,MOGA和原SPEA2)作为参照,与所提出的改进SPGA2算法进行对比试验.NSGA以帕累托解的支配关系为搜索策略,具备很强的非支配解全局搜索能力[25];VEGA是通过分配多个向量组评估优化多个目标,其生成的解多聚拢在单目标极值点处,局部优化能力较强;MOGA通过权重将多目标聚合成单个目标,再通过遗传算法对单目标优化,其具备较强的收敛能力,然而固定的目标权重会影响算法的全局搜索能力[26];原SPEA2是未经改进的强帕列托支配进化算法,其个体的支配信息和被支配信息由强度值体现,具备较强的解空间定向寻优搜索能力[23].本文所提出的改进SPGA2算法在结合SPEA2和GA算法的基础上,引入局部搜索策略,以弥补面对割裂不连续的最优边界制约算法收敛能力的情况,在保障SPEA2全局搜索能力的同时,增强对局部最优边界的搜索效率. Fig. 5 Performance comparison of multi-objective algorithms图5 多目标算法性能对比 本文选取非支配解比例和算法收敛距离2个指标来衡量和对比多目标算法的性能.非支配解比例是通过多次迭代后产生的最终解集中非支配解的数量占初始解集中解数量的百分比,体现了整体寻优能力.如图5(a)所示,改进SPGA2虽在寻优过程初期非支配解数量增长较慢,然而经过多次迭代最终生成的支配解比率最高;VEGA初期支配解比率增长对比NSGA较快,而后者最终支配解比率稳定值却高于前者;VEGA和MOGA只考虑不同目标空间的权重问题,不关注解的支配关系,故其最终的非支配解比率较低;原SPEA2初期支配解比率增长较快,而其最终支配解比率稳定值同NSGA相似,显著低于改进SPGA2的值. 本文将算法迭代过程中历代最优解集的并集中非支配解的合集定义为参考集,理想的帕列托最优解集应是向该参考集无限逼近.通过计算每代种群中所有个体解到参考集的欧氏距离之和,将其记为该代种群的收敛距离,并对其标准化.如图5(b)所示,MOGA和VEGA关注不同目标权重下的最优解,忽略解的支配关系,故搜索质量不佳,最终收敛距离较远;原SPEA2和NSGA强调全局搜索能力,忽略部分的局部最优解,导致收敛速度较慢.而改进SPGA2算法在收敛性能上有了较大程度的提高,一方面收敛的速度更快,另一方面最终收敛距离也距最优边界最近.收敛速度的加快是算法中引入了局部优化搜索策略的影响,大大增加了解空间的探索效率,减少无意义的迭代,使得进化过程更有针对性;最终收敛距离缩短是改进算法整体优化的结果,体现了算法在全局搜索能力和最终解集有效性上的优异表现,在减少了计算负担的同时也提高了收敛能力. 此节讨论不同任务程结构和不同服务资源数量对任务分配模型的影响,选取4种不同的业务流程,其结构分别包含8,12,20,25个任务单元;并设置服务资源数量n(S)分别为4,8,12,15,以探究不同任务结构和不同服务资源数量对该多目标分配模型的影响. 多目标任务分配问题以帕列托非支配解为主要参考基准,在所有非支配解集中通过管理者对不同目标的偏好来选择出优秀解.而帕列托解集中除了支配关系,难以比较2个解的优劣之分.本文寻找特定解空间中的最优解点,通过比较最优解在3个目标函数中的得分情况,验证不同任务结构和服务数量对任务分配模型的影响.特定解空间的最优解是通过设定每个目标维度的限制范围,从符合要求的解集中找出最优解点.本文设置4种任务结构和4种服务资源数目形成16组任务分配问题,限定每个目标值需大于0.55,通过特定解空间限制{x,y,z|x>0.55,y>0.55,z>0.55}找出最优解,不同流程和服务资源中任务分配方案最优解的目标值对比情况如图6所示: Fig. 6 Comparison under different task and resource schemes图6 不同任务和资源方案下最优解目标值对比情况 从图6中可以看出,任务结构和资源数对时间目标影响较大,简单和普通结构的流程分配到8个服务资源的场景可以获得最高时间目标值,而对于大型复杂流程,8,12,15个不同服务资源数量对时间目标值的影响不显著,故对待大型复杂流程增加服务资源数目所起作用不明显.对于成本目标,本文假设云服务按使用时间收费,且服务能力跟资源的单位时间成本正相关,即越贵的服务速度越快,任务运行完成耗时越短.可看出不同任务结构复杂程度和资源数量情况下任务运行成本变化较为平稳,对成本影响较低.信任目标值中,随着服务资源数量增加,信任目标值呈显著增长趋势,是因为引入更多的服务资源扩展了任务分配过程中的可信资源范围;而不同任务规模的流程影响其信任目标值的变动并不大,显示了任务结构复杂度变化对信任目标值变化的影响较低. Fig. 7 Trust situation in multi-objective task assignment model图7 多目标任务分配模型中的信任情况 考虑到云服务系统中任务分配问题是基于可信服务的,故此节将模型中的信任问题单独提取出做独立分析.选取包含12个任务的普通业务流程和4个不同属性的服务资源作为实验对象.首先验证了50次算法迭代中,每代群体中所有非支配解的信任目标平均值,并表示在图7(a)中.图7(a)中除了展示非支配解集的平均信任情况,还标识出任务对可信服务所要求的最低信任阈值,即流程中所有任务最低信任需求值的和.由图7(a)可以看出,一方面由于信任约束的限制,使得算法进化过程中所有任务的信任需求都得到满足,保证每次分配都符合信任约束;另一方面,算法迭代中整个帕列托解集的信任目标均值保持稳定增加,且最终生成解集的信任均值稳定在0.6左右,体现了任务分配方案最终解是基于高可信度的. 进化中的信任目标均值体现了算法迭代过程中整体的信任变化情况,而针对某次任务分配方案中的信任分布情况就需要选取具体的解进行分析.本文提出基于理想点的最优解确认方案,以选出合适的最优解点来分析其信任分布情况.先通过算法迭代得出最终的帕列托解集,在解集中设置理想点,并选择与理想点欧氏距离最短的解点作为最优解.本文设置理想点为(0.6,0.6,0.6),通过搜索帕列托解空间中与理想点欧氏距离最小的非支配解点作为最优解.以该最优解为例,对其任务分配方案的信任分布情况进行分析.如图7(b)所示,每根柱状图代表该任务单元所分配的信任情况,柱状图下半部分为每个任务单元的信任约束值,上半部分为任务所分配的服务资源的可信度超过信任阈值部分.由图7可见,在信任约束下所有任务单元的最小信任值需求都得到满足,且在信任目标推动下,高可信需求的任务分配到了更可信的服务资源,大大保障了整个服务系统的可信性. 算法的时间复杂度将直接影响其运行质量和效率,现对本文所提出的改进SPGA2算法中各算子的时间复杂度进行分析,取最大值为算法的时间复杂度.假设多目标任务分配模型是将n个任务分配到m个资源上. 1) 种群初始化.对种群P和存档集Q进行初始化操作,其空间大小分别为常数Np和Nq.根据初始化原则,随机生成Np×n×m个数据,并令存档集为空集.故种群初始化复杂度为O(m×n). 2) 遗传算子.群体交叉操作的复杂度为Np×O(m2×n)=O(m2×n);变异操作的复杂度为Np×O(m×n)=O(m×n).故遗传算子的复杂度为O(m2×n)+O(m×n)=O(m2×n). 3) SPEA2算子.该算子中个体的强度值表示其支配和被支配的信息,在计算个体的强度值时,需要计算个体间欧氏距离,其时间复杂度为O(m2×n2).而在环境选择过程中,复杂度为(Nq+1)2×Nq×O(m2×n2).故SPEA2算子的复杂度为O(m2×n2)+(Nq+1)2×Nq×O(m2×n2)=O(m2×n2). 4) 局部搜索算子.对历代存档集中的非支配个体进行邻域搜索,其种群最大交换次数为Np×n×m×m,故局部搜索算子的复杂度为O(m2×n). 在改进SPGA2算法中,SPEA2算子时间复杂度较高,为O(m2×n2);遗传算子和局部搜索算子复杂度其次,为O(m2×n);种群初始化复杂度最低,为O(m×n).故改进SPGA2算法的时间复杂度为O(m2×n2).算法中复杂度最高为通过欧氏距离计算个体的强度值,由于强度值的计算为SPEA2算子的必要流程,故本文所引入的算子并未增加算法的时间复杂度. 云计算等新兴信息技术带来了产业链重新整合和商业模式创新等一系列重大变革,面对日益增长的业务需求和复杂变化的商业环境,企业如何改造并升级业务流程、合理分配和使用云服务资源、在安全可信服务的基础上提高效率并降低成本,成为其保持旺盛生命力的重要保障.本文在面向服务的框架基础上,结合混合云服务模式和信任机制,构建了一种基于混合云的可信云服务系统体系架构,并在该框架下建立了基于时间、成本和信任的多目标任务分配模型;引入信任值的度量以刻画任务的信任需求和服务资源可信度,并于任务分配中结合信任机制选择云服务资源,以保证服务的安全可靠性;在此基础上,梳理了6种典型任务结构关于多目标的函数范式;采用基于局部搜索策略的改进SPGA2算法提高了混合云环境下多目标任务分配问题解空间的搜索效率,并最终通过仿真实验验证了模型和算法切实有效可行. 在未来的工作中,我们将收集并使用企业实际的业务流程数据,并结合市场上现有的典型云服务资源定价策略和服务能力,通过实际数据进一步验证模型的有效性.现模型中引入的信任是融合直接信任值和推荐信任值的云服务综合信任情况,今后我们拟结合不同云环境下的跨地域和跨结构的多域信任属性特征,研究云环境下信任的跨域传播和更新等问题,建立一种动态的综合跨域信任网络,以更好地刻画服务系统中的信任关系,进一步增强系统的安全可信性. [1]Zhan Zhihui, Liu Xiaofang, Gong Yuejiao, et al. Cloud computing resource scheduling and a survey of its evolutionary approaches[J]. ACM Computing Surveys, 2015, 47(4): 1-33 [2]Lin Chuang, Su Wenbo, Meng Kun, et al. Cloud computing security: Architecture, mechanism and modeling[J]. Chinese Journal of Computers, 2013, 36(9): 1765-1784 (in Chinese)(林闯, 苏文博, 孟坤, 等. 云计算安全: 架构、机制与模型评价[J]. 计算机学报, 2013, 36(9): 1765-1784) [3]Dorsch C, Häckel B. Combining models of capacity supply to handle volatile demand: The economic impact of surplus capacity in cloud service environments[J]. Decision Support Systems, 2014, 58(1): 3-14 [4]Boru D, Kliazovich D, Granelli F, et al. Energy-efficient data replication in cloud computing datacenters[J]. Cluster Computing, 2015, 18(1): 385-402 [5]Luo Junzhou, Jin Jiahui, Song Aibo, et al. Cloud computing: Architecture and key technologies[J]. Journal on Communications, 2011, 32(7): 3-21 (in Chinese)(罗军舟, 金嘉晖, 宋爱波, 等. 云计算: 体系架构与关键技术[J]. 通信学报, 2011, 32(7): 3-21) [6]Li Qiao, Zhen Xiao. Research survey of cloud computing[J]. Computer Science, 2011, 38(4): 32-37 (in Chinese)(李乔, 郑啸. 云计算研究现状综述[J]. 计算机科学, 2011, 38(4): 32-37) [7]Ahmed W, Wu Yongwei, Zheng Weimin. Response time based optimal Web service selection[J]. IEEE Trans on Parallel & Distributed Systems, 2013, 26(2): 551-561 [8]Wei Wei, Liu Yang, Yang Weidong. A fast approximation algorithm for the general resource placement problem in cloud computing platform[J]. Journal of Computer Research and Development, 2016, 53(3): 697-703 (in Chinese)(魏蔚, 刘扬, 杨卫东. 一种通用云计算资源调度问题的快速近似算法[J]. 计算机研究与发展, 2016, 53(3): 697-703) [9]Mao Chengying, Chen Jifu, Towey D, et al. Search-based QoS ranking prediction for Web services in cloud environments[J]. Future Generation Computer Systems, 2015, 50(C): 111-126 [10]Liu Hongbo, Abraham A, Mcloone S. Swarm scheduling approaches for work-flow applications with security constraints in distributed data-intensive computing environments[J]. Information Sciences, 2012, 192(6): 228-243 [11]Topcuouglu H, Hariri S, Wu Minyou. Performance-effective and low-complexity task scheduling for heterogeneous computing[J]. IEEE Trans on Parallel & Distributed Systems, 2002, 13(3): 260-274 [12]Wen Yun, XuHua, Yang Jiadong. A heuristic-based hybrid genetic-variable neighborhood search algorithm for task scheduling in heterogeneous multiprocessor system[J]. Information Sciences, 2011, 181(3): 567-581 [13]Feng Dengguo, Zhang Min, Zhang Yan, et al. Study on cloud computing security[J]. Journal of Software, 2011, 22(1): 71-83 (in Chinese)(冯登国, 张敏, 张妍, 等. 云计算安全研究[J]. 软件学报, 2011, 22(1): 71-83) [14]Fang Yulin, Qureshi I, Sun Heshan, et al. Trust, satisfaction, and online repurchase intention: The moderating role of perceived effectiveness of E-commerce institutional mechanisms[J]. Mis Quarterly, 2014, 38(2): 407-427 [15]Yu Nenghai, Hao Zhuo, Xu Jiajia, et al. Review of cloud computing security[J]. Acta Electronic Sinica, 2013, 41(2): 371-381 (in Chinese)(俞能海, 郝卓, 徐甲甲, 等. 云安全研究进展综述[J]. 电子学报, 2013, 41(2): 371-381) [16]Krautheim F J, Phatak D S, Sherman A T. Introducing the trusted virtual environment module: A new mechanism for rooting trust in cloud computing[G]Trust and Trustworthy Computing. Berlin: Springer, 2010: 211-227 [17]Manuel P. A trust model of cloud computing based on quality of service[J]. Annals of Operations Research, 2015, 233(1): 281-292 [18]Li Yongjun, Dai Yafei. Research on trust mechanism for peer-to-peer network[J]. Chinese Journal of Computers, 2010, 33(3): 390-405 (in Chinese)(李勇军, 代亚非. 对等网络信任机制研究[J]. 计算机学报, 2010, 33(3): 390-405) [19]Xu Feng, Wang Yuan, Zhang Lin, et al. A trust chain discovery algorithm for open environment[J]. Journal of Computer Research and Development, 2006, 43(Suppl2): 72-77 (in Chinese)(徐锋, 王远, 张林, 等. 一个开放环境中信任链发现算法的设计与分析[J]. 计算机研究与发展, 2006, 43(增刊2): 72-77) [20]Ko R, Jagadpramana P, Mowbray M, et al. TrustCloud: A framework for accountability and trust in cloud computing[C]Proc of the 2011 IEEE World Congress on Services. Los Alamitos, CA: IEEE Computer Society, 2011: 584-588 [21]Shu Jian, Liang Changyong. Dynamic trust model based on DS evidence theory under cloud computing environment[J]. Computer Science, 2016, 43(8): 105-109 (in Chinese)(束柬, 梁昌勇. 基于DS理论的多源证据融合云安全信任模型[J]. 计算机科学, 2016, 43(8): 105-109) [22]Chinosi M, Trombetta A. BPMN: An introduction to the standard[J]. Computer Standards & Interfaces, 2012, 34(1): 124-134 [23]Kim M, Hiroyasu T, Miki M, et al. SPEA2: Improving the performance of the strength pareto evolutionary algorithm 2[G]LNCS 3242: Proc of Int Conf on Parallel Problem Solving from Nature. Berlin: Springer, 2004: 742-751 [24]Silverman B W. Density Estimation for Statistics and Data Analysis[M]. London: Chapman &Hall, 1986 [25]Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Trans on Evolutionary Computation, 2002, 6(2): 182-197 [26]Gen M, Lin Lin. Multi-objective evolutionary algorithm for manufacturing scheduling problems: State-of-the-art survey[J]. Journal of Intelligent Manufacturing, 2014, 25(5): 849-866 ShuJian, born in 1989. PhD. His main research interests include cloud computing, information management, information security, and trust theory. LiangChangyong, born in 1965. PhD, professor, PhD supervisor. His main research interests include information system & information management, cloud service, and decision science. XuJian, born in 1982. PhD candidate. His main research interests include big data, data mining, game theory, and machine learning.4 仿真实验
4.1 算法的可用性和有效性
4.2 多目标优化算法对比分析
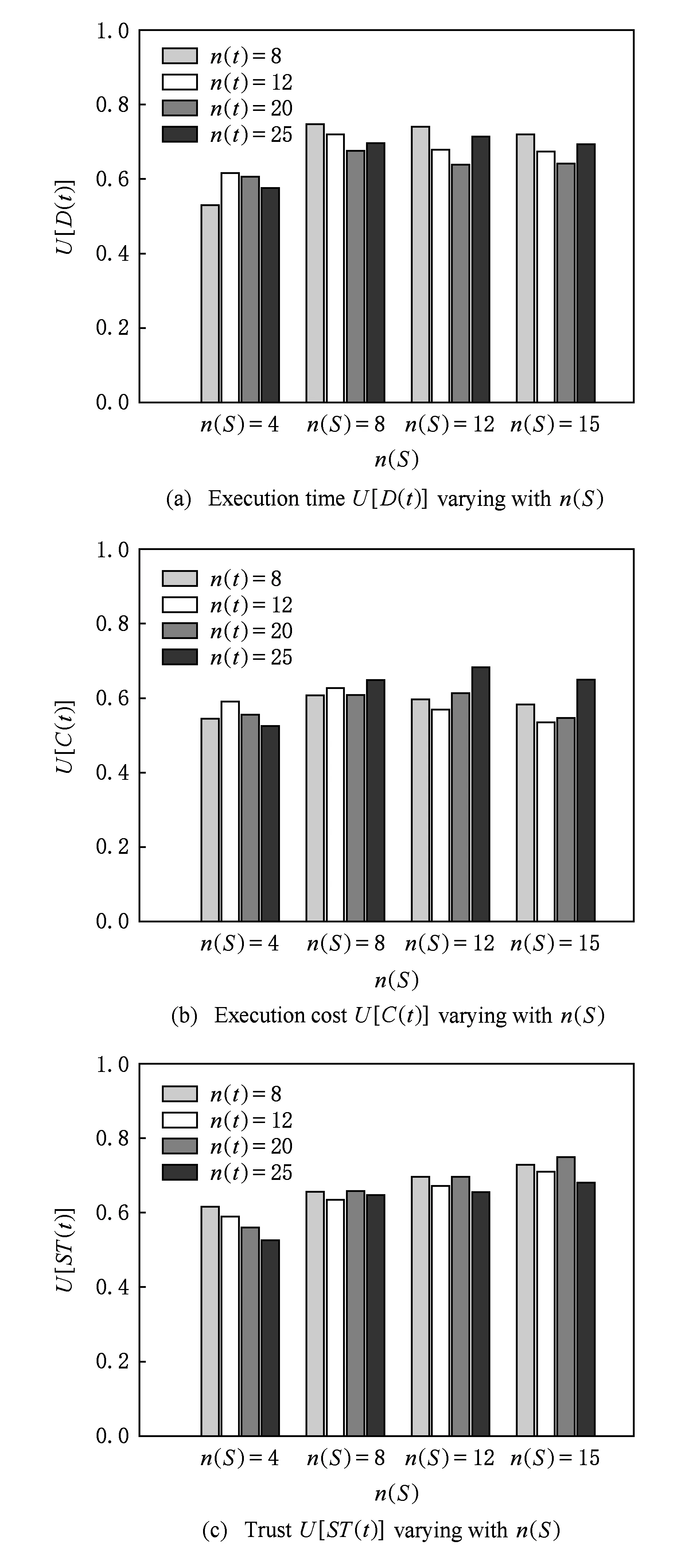
4.3 任务结构和资源数量对分配模型的影响分析
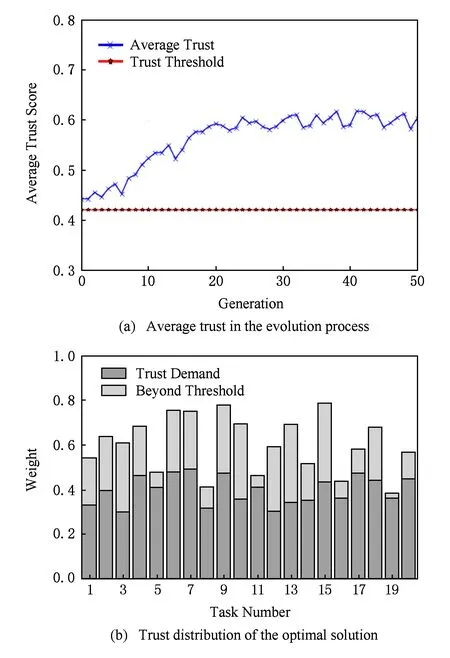
4.4 任务分配模型中的可信度分布及变化情况
4.5 时间复杂度分析
5 总结与展望



