基于球杆仪的立式加工中心圆度的测试与分析*

刘志松，王永青，刘 阔

(大连理工大学 机械工程学院 精密与特种加工教育部重点实验室，辽宁 大连 116024)

0 引言

精密与超精密加工仍然是现代机械制造中的重要组成部分和未来发展的方向[1]，随之广泛的应用对数控机床的精度提出了更高的要求。数控机床误差的检测对其精度的提高具有重要的意义。传统的机床精度检测方法，如激光干涉仪，检测精度高，但操作复杂，成本也比较高。因此，实现对机床精度进行快速、方便、经济的测量，具有较大的现实意义。

球杆仪系统提供了一种测量数控机床常见误差的有效方法[2]。该方法可以实现机床动态轮廓精度的测量，分离各影响因素的误差。球杆仪还具有便于携带和易于安装等优点，被广泛的应用于机床精度的评价和诊断[3]，已经被ISO230[4]和ASME B5.54[5]等采纳为检测机床圆运动和精度检验的标准工具。国内外很多学者也利用球杆仪对做了很多的测试。Tian等[6]利用双头球杆仪对3-DOF主轴进行了动态标定。Lee等[7]利用双头球杆仪对五轴(含一个摆头)机床几何误差进行了识别和测量。参考文献[8-10]针对不同机床，利用球杆仪检测技术，提出了对其几何误差或者空间误差的检测方法以及补偿模型。

以上研究中很多给吹圆度误差与进给速度的关系，但没有剖析其原因。本文采用双头球杆仪对某立式加工中心圆度误差进行测试，测试包含X-Y，Y-Z和Z-X平面内的误差，并且在多进给速度下进行测试，对测试结果中圆度误差影响因素分离，并对测试结果分析，为提高加工精度提供参考。

1 误差形式的介绍

立式加工中心的圆度会受到反向间隙、横向间隙、周期误差、比例不匹配、伺服不匹配、反向跃冲、垂直度以及X/Y轴直线度等因素影响[11]。其中，垂直度、伺服不匹配、反向跃冲、直线度、比例不匹配对圆度的影响较大。

(1)垂直度

垂直度误差是指测试机器的X轴和Y轴相互不为90°。垂直度误差对加工的影响是，会使加工形状呈椭圆或花生形，沿45°或135°对角方向拉伸变形，拉伸量不受进给率的影响，如图1a所示。

(2)反向越冲

反向跃冲是圆运动轨迹在经过轴线时产生一个小尖峰，如图1b所示。尖峰大小通常随机器的进给率增加而增大。导致该问题的可能原因有：该轴驱动电机输出的扭矩不够，造成在换向处由于摩擦力的方向发生改变而出现粘性停顿；机器在进行反向间隙补偿时伺服响应时间不准确，机器不能准时地对反向间隙施加补偿，导致轴出现停顿；伺服响应在伺服换向点很差，导致在轴停止一个方向运动和开始另一方向运动之间出现短暂时延。

(3)伺服不匹配

伺服不匹配就是两根伺服轴存在时间的上的不同步，通常以一根伺服轴超前于另一伺服轴的时间表示，单位以毫秒计。伺服不匹配会导致图形呈椭圆或花生形，沿45°或135°对角方向拉伸变形，如图1c所示。通常随着进给率的增加，拉伸变形量也会增加。伺服不匹配将导致插补圆不圆。

(4)周期误差

周期误差表现为沿图形频率、幅度均发生变更的周期性正弦曲线误差。周期误差在X轴或者Y轴方向的误差波长的变化率近似为常数。对加工的影响形式如图1d所示。形成周期误差有如下几种可能的原因：该轴滚珠丝杠的螺纹磨损导致其在运动时无法保持匀速而出现正弦方式。位置反馈系统的安装可能有偏心。滚珠丝杠安装可能有偏心。细分装置或感应式传感器未调整好。

(5)比例不匹配

比例误差是指在测试过程中被测量轴间的行程差。例如，如果机器在XY平面内运行整个圆，X轴和Y轴运行的距离应完全相同。如果有不同，两轴间运动位置差就是比例不匹配误差。如图1e中所显示的a和b之间的差异。比例不匹配会使加工图形呈椭圆或花生形，沿0°或90°轴方向拉伸变形。

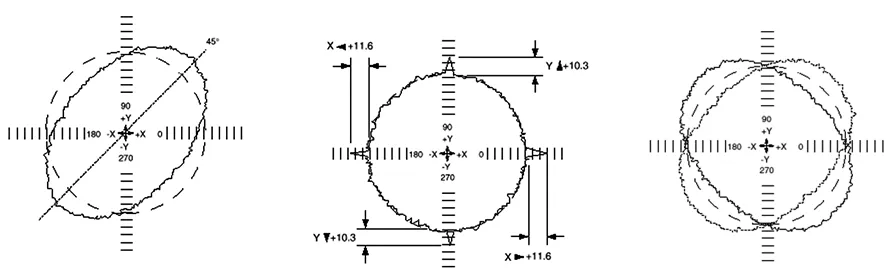
(a)垂直度误差 (b)反向越冲 (c)伺服不匹配

(d)周期误差 (e)伺服不匹配图1 几种常见的误差形式示意图

2 基于球杆仪的圆度测试原理

通过两轴联动，实现主轴上刀具相对于工作台上固定的工件在X-Y、Y-Z和X-Z平面内圆周或者圆弧运动。利用球杆仪可以自定义空间测量轨迹的功能，实现在上述三个平面内运动轨迹的圆度测量。

其测试原理是：设工作台上磁力座上精密球的球心为坐标系的原点，为主轴上精密球球心(刀尖)的名义坐标，当机床运动到目标位置时，设球心的实际位置为。则机床的空间误差可如下表示[12]。

Δx=x′-x
Δy=y′-x
Δz=z′-x

(1)

式(1)为点位移误差，并且三者满足：

(R+ΔR)2=x′2+y′2+z′2=

(2)

其中，R为理论半径，忽略误差项中3个高阶小量，化简上式可得:

ΔR=(xΔx+yΔy+zΔz)/R

(3)

式(3)表示主轴上定点P的定位误差和球杆仪测得的半径误差之间的关系，用于机床圆度误差的测量。

3 试验设备以及测试情况

圆度测试采用Renishaw公司的QC20-W无线球杆仪，其是由球杆仪本体和精密磁力碗座构成，见图2。球杆仪本体是一个高精度伸缩式线性位移传感器，在两端均有一个精密球，用于与磁力碗座连接。磁力碗座分别连接机床工作台和机床主轴，如图3所示。

图2 球杆仪测试意图

测试机床为VMC850E型立式加工中心，VMC850E立式加工中心 。可用于航天航空，汽车零件，机械加工及模具制造领域，适应于中、小型零件的高精度与高效率的加工和钻、铣、攻、镗的自动化加工，如图4所示。其部分参数如表1所示。

表1 VMC850E立式加工中心参数

图3 球杆仪安装示意图

图4 测试机床结构图

图5 球杆仪测试空间示意图

测试时，由于被测试机床的自身特性，最大测试空间为一半球状，如图5所示。测试在机床XY平面内做完整圆周运动，在YZ平面和ZX平面做半圆周运动，圆周运动半径为100mm。测试分别在500mm/min、1000mm/min、1500mm/min、2000mm/min、2500mm/min和3000mm/min进给率下进行，对应采样频率分别为20Hz、40Hz、58.824Hz、76.923Hz、100Hz、125Hz。每种试验测试条件下测试两次，每次测试均包含顺时针运行和逆时针运行。在XY平面内，500mm/min进给率下测试结果如图6所示，运行1为顺时针运行，运行2为逆时针运行。

图6 500mm/min进给率下XY平面内圆度误差测试结果

利用球杆仪配套的系统软件可以直接读出各个平面内圆度误差的测量值，测量结果如图7～图9所示。

图7 XY平面内圆度误差测试

图8 YZ平面内圆度误差测试

图9 ZX平面内圆度误差测试

在XY平面内进行的是完整的圆度测试，通过软件还对平面误差的各项来源大小及其所占的比例进行了测试。部分误差项测试数据如表2所示。

表2 部分测试的误差

将各项误差量按照一定转化规则转化成对圆度误差的影响，并计算出他们在圆度误差中所占的比例，它们所占的比例以及其随速度变换的情况如图10所示。

图10 不同转速下各项误差占圆度误差的比例

4 测试结果分析

XY平面圆度测试时，顺时针测量圆度误差与逆时针测量存在相对恒定大小的误差值。这可能是由于测量中都是先顺时针测量，然后逆时针测量，存在反向间隙，造成误差。

XY、YZ、ZX三个平面圆度误差的测试结果显示，圆度误差随进给速率的提高而增加，并且近似为线性关系。选用简单线性回归，以进给速率为自变量、以平面圆度误差为因变量描述进给速率与圆度误差的关系。

yi=β0+β1xi+εi

(i=1，2，…，n)

(4)

其中，yi是因变量的第i个观察值，xi为自变量的第i个观察值，β0与β1为回归系数，εi为随机误差。

采用最小二乘法对回归方程进行估计得：

(5)

将平面圆度误差与进给速率带入上述方程，得到经验回归方程(不含误差项)：

yXYi=23.59+0.0240xXYi
yYZi=25.76+0.0054xYZi
yZXi=18.34+0.0178xZXi

(6)

三个方程的拟合优度R2分别为0.994、0.867、0.993。

结合表1中数据以及图10分析进给速率提升对圆度误差的原因。随着进给速率提高，伺服误差没有太大变化，而伺服误差在总误差中所占的比例越来越高。这是由于伺服所造成的误差δ是由伺服误差时间Δt与进给速率v相乘得到的，即δ=v×Δt。故进给速率越大，伺服误差对圆度误差的影响越大，进而使得圆度误差随进给速率线性增加。

5 结束语

立式加工中心圆度的检测是评价机床精度的重要因素之一。本文通过球杆仪对立式加工中心快速检测，得到空间圆度误差，并对误差分析得到以下结论：

(1)伺服不匹配、垂直度、横向间隙、比例不匹配、周期误差、反向间隙和反向跃冲所造成的误差占据了加工圆度误差的主要部分。

(2)立式加工中心各坐标平面圆度误差与机器进给速度近似成正比，其原因是伺服误差与进给速率成正比，并且伺服误差随进给速度增加成为圆度误差主要影响因素。

[参考文献]

[1] 王家兴，郭宏伟，赵峰，等. 基于球杆仪的数控车床几何误差检测和补偿[J]. 制造技术与机床, 2011(10): 132-136.

[2] 仇健，王冠明，葛任鹏. 基于球杆仪的卧式五坐标加工中心圆度误差诊断[J]. 制造技术与机床, 2013(8): 39-42.

[3] 何振亚，傅建中，陈子辰. 基于球杆仪检测五轴数控机床主轴的热误差[J]. 光学精密工程, 2015, 23(5): 1401-1408.

[4] The Internationah Organization for Standardization. ISO 230-4-1996 Test code for machine tools-Part4: Circular tests for numerically controlled machine tools[S].Geneva: International Standard Organization, 1996.

[5] COMMITTEE A N S. ASME B5.54-2005 Methods for performance evaluation of numerically controlled machine tools[S].New York: The America Society of Mechanical Engineers, 2005.

[6] TIAN W, YIN F, LIU H, et al. Kinematic calibration of a 3-DOF spindle head using a double ball bar[J]. Mechanism and Machine Theory, Elsevier Ltd., 2016, 102: 167-178.

[7] LEE D M, ZHU Z, LEE K I, et al. Identification and measurement of geometric errors for a five-axis machine tool with a tilting head using a double ball-bar[J]. International Journal of Precision Engineering and Manufacturing, 2011, 12(2): 337-343.

[8] 郝云，刘海华，汤秋，等. 镗铣加工中心动态误差的检测研究[J]. 制造技术与机床, 2017(2): 33-36.

[9] 封志明，殷国富. 基于球杆仪的数控机床空间误差建模与检测方法研究[J]. 西华大学学报(自然科学版), 2014, 33(4): 20-23.

[10] 张大卫，商鹏，田延岭，等. 五轴数控机床转动轴误差元素的球杆仪检测方法[J]. 中国机械工程, 2008, 19(22): 2737-2741.

[11] RENISHAW PLC. RENISHAW[M]. Ballbare Help: Ballbare 20HPS software, 2009.

[12] 张虎，周云飞，唐小琦，等. 数控机床空间误差球杆仪识别和补偿[J]. 机械工程学报, 2002, 38(10): 108-113.