立铣刀磨削加工中进退刀方法研究*

李 乐，唐 晓，程雪锋，江 磊，丁国富

(西南交通大学 机械工程学院，成都 610031)

0 引言

铣削加工是一种重要的切削加工方法，其加工范围较广，可以适应多种几何表面的加工。随着铣削加工工艺的发展，复杂结构立铣刀的磨削加工方法成为重要的研究课题，国内外很多学者做了大量研究。其中罗伯勋研究了S形刃球型立铣刀前刀面的数学模型[1]；Yuan等研究了球头刀的部分加工原理[2-3]；Shangjian、刘井玉、李长映等研究了球头刀的多轴联动数控加工方法[4-6]；汪羿等研究了立铣刀刃磨中的参数优化问题[7]；范运金、刘建军等研究了立铣刀加工的软件拓展和加工仿真等问题[8-9]。现有的研究主要针对立铣刀各种结构的加工方法，对五轴磨削加工过程中进退刀方法的研究较少。其他关于铣削加工进退刀的方法对磨削加工有一定指导意义[10]，但也不能完全适用到磨削加工中。五轴磨床的主轴上安装着由多个砂轮组成的砂轮组，不同工步可能使用不同的砂轮，加工过程中直接使用相应位置的砂轮进行加工而不是安装新砂轮。工步间的砂轮切换可能导致砂轮和毛坯之间发生碰撞，需要研究一套可靠的进退刀方法。

本文针对该问题，研究了立铣刀五轴磨削加工特点，提出一种基于砂轮毛坯干涉检测坐标系的进退刀方法，分别计算出安全位置、快速逼近位置和进退刀路径，解决了不同结构五轴磨床在加工立铣刀具中工步间的进退刀安全问题。基于该方法在C#平台上开发了一套刀具磨削加工进退刀处理软件，并进行了仿真验证。

1 砂轮毛坯干涉检测坐标系

不同结构的磨床刀具夹头和砂轮组的方向有很大区别，如图1所示两种结构的磨床，毛坯的装夹方式和砂轮的安装方向不同，导致工步间的进退刀方式存在较大区别，主要区别表现为C′-B型磨床最终从Z轴方向进刀，而A′-C型磨床最终从X轴方向进刀。

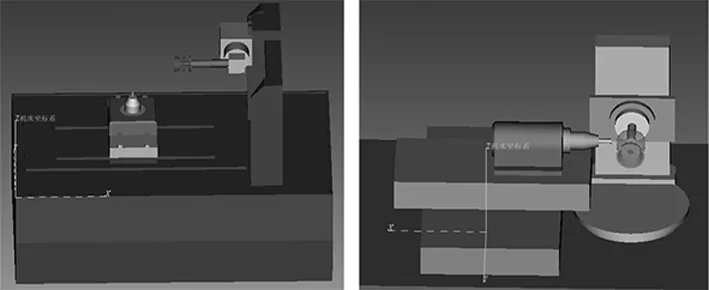
(a)C′-B结构的磨床 (b)A′-C结构的磨床图1 两种不同结构的磨床模型

为了建立一种能够适应各种磨床结构的进退刀数学模型，需要采用一种通用的方式定义砂轮组和毛坯的位置关系。本文以毛坯装夹点为原点，毛坯中心轴为Z方向，以砂轮组轴向为X方向，建立砂轮毛坯干涉检测坐标系OS-XSYSZS。在该坐标系下，不同结构磨床的砂轮组和毛坯具有统一的初始位置关系，具体如图2所示。为了简化处理，这里将平行砂轮、碗型砂轮和碟型砂轮全部视为包围砂轮的最小圆柱体，其中(Li,i=1,2)…为砂轮安装位置，(di,i=1,2…)为砂轮直径。

图2 干涉检测坐标系和砂轮组参数

根据构建砂轮毛坯干涉检测坐标系的方法，求解机床坐标系和OS-XSYSZS坐标系之间的坐标变换矩阵。定义Os-XsYsZ坐标系到机床坐标系下的坐标变换矩阵为：

(1)

其中，(it,jt,kt)为砂轮在机床坐标系下的初始轴方向单位矢量，(iw,jw,kw)为机床坐标系下的毛坯中心单位矢量。按右手坐标原则可得：

(iy,jy,ky)=(iw,jw,kw)×(it,jt,kt)

(2)

2 安全位置计算

磨削过程中工步之间需要切换加工砂轮时，砂轮的加工姿态一般会发生变化，使得两个工步的转轴转角变化较大。所以在一个工步加工完成时需要先退刀到安全位置，然后再将转轴旋转到下一个工步的初始加工姿态上。安全位置需要保证磨床两个旋转轴任意转动，砂轮组和毛坯不会发生干涉。在OS-XSYSZS坐标系下分别计算安全位置在XS,YS,ZS坐标轴上的坐标，再将其转换到机床坐标系下。

XS轴方向的安全坐标为XH，则：

XH=-(Hp+RP+δ)

(3)

其中，Hp=Max{Li}为最大砂轮安装位置；Rp=Max{di/2}为最大砂轮半径；i=1,2…,n为砂轮编号；δ为安全阈值。

毛坯夹头所在的旋转轴与毛坯在同一条轴线上，其旋转不改变毛坯和砂轮整体的位置关系，所以平面XSZS为砂轮和毛坯的相对旋转的平行平面，即另一转轴的旋转导致的砂轮和毛坯之间的相对旋转一定平行于XSZS平面。同一个毛坯的加工过程，砂轮总是在XSZS平面的一侧，具体是哪一侧可以通过该工步第一加工刀轨的G代码(x1,y1,z1,r41,r51)确定。设Dy=+1表示砂轮在XSZS平面的+YS一侧，Dy=-1在-YS一侧，则：

(4)

YS轴方向的安全坐标为YH，则：

YH=Dy·(Rp+RB+δ)

(5)

其中，RB为毛坯半径。

ZS轴方向的安全坐标为ZH，则：

ZH=Rp+Lc+δ

(6)

其中，Lc为毛坯装夹长度。

将OS-XSYSZS坐标系下的安全位置转换到机床坐标系下：

(X,Y,Z)T=Msm·(XH,YH,ZH)T

(7)

其中，X,Y,Z分别为机床坐标系下的安全位置坐标。

3 快速逼近位置计算

安全位置距离实际加工位置有较大的进刀距离，需要先快速逼近到距离加工刀轨较近的位置，再开始加工。该快速逼近位置需要保证当前工步中第一个刀轨对应的砂轮姿态下，当前加工砂轮和毛坯不会发生干涉。求解每个砂轮在OS-XSYSZS坐标系下的XS坐标值，以其绝对值最小为判据，得到当前加工砂轮。

OS-XSYSZS坐标系下第一个刀轨对应坐标：

(8)

OS-XSYSZS坐标系下每个砂轮XS坐标值为：

xtsi=xs1+Li·cos(r51);i=1,2…n

(9)

比较所有砂轮的xtsi值，绝对值最小的砂轮为当前加工砂轮，设其编号为m。

为了保证快速逼近位置的安全性，本文采用投影法来判断当前加工砂轮与毛坯的位置关系。如图3所示，将当前加工砂轮的包围体和毛坯投影到XSZS平面上，如果投影相交，则需要在ZS方向上添加一个补偿值εz来保证两个投影不相交。

图3 砂轮毛坯投影关系

要保证两个投影矩形不相交，只需要当前加工砂轮投影的4个顶点{P1,P2,P3,P4}的ZS坐标值都大于毛坯装夹长度Lc。计算{P1,P2,P3,P4}的ZS坐标值：

(10)

其中，Lm为当前加工砂轮安转位置；Hm为当前加工砂轮厚度。

{P1,P2,P3,P4}的Z坐标值最小值为：zpmin=Min{zp1,zp2,zp3,zp4}，则安全补偿值εz为：

(11)

转换到机床坐标系下，快速逼近位置坐标为：

(X0,Y0,Z0)T=(x1,y1,z1)T+(σ+εz)·Msm·(0,0,1)T

(12)

4 进退刀路径

安全位置和快速逼近位置保证了两个位置上砂轮和毛坯不会发生干涉。实际加工中要将砂轮从刀轨加工结束位置快速退刀到安全位置，然后旋转两个转轴来调整砂轮姿态，再从安全位置快速进刀到快速逼近位置，最后从快速逼近位置按照进给速度开始加工。其中快速进退刀过程需要按照一定顺序，每次只进行一个运动轴的运动，以保证进退刀过程的安全性。

由磨削加工特点可知，刀轨结束时砂轮和毛坯处于分离状态，退刀过程中只要先在YS方向上退刀到安全坐标，再分别沿ZS和XS方向移动到安全坐标，就可以保证退刀过程的安全。

机床坐标系下三次退刀方向矢量分别为：

(13)

三次退刀的总退刀量为：

(Δx0,Δy0,Δz0)=(X,Y,Z)-(xf,yf,zf)

(14)

其中，xf,yf,zf为上一工步的最后刀轨的加工坐标。

三次退刀位置分别为：

(15)

退刀到安全位置后，旋转机床转轴到下一个工步首行加工转角上，然后按照XS→YS→ZS顺序快速进刀到快速逼近位置。按照上面方法，三次进刀方向矢量分别为：

(16)

三次进刀的总进刀量为：

(Δx1,Δy1,Δz1)=(X0,Y0,Z0)-(X,Y,Z)

(17)

三次进刀位置分别为：

(18)

5 方法验证

基于上述进退刀方法，用C#开发了一套立铣刀磨削加工进退刀处理软件。该软件可以实现多种结构磨床加工立铣刀过程中进退刀代码的计算。用户只需要输入毛坯装夹长度、砂轮安装位置和机床最大退刀位置等参数，结合刀轨中包含的砂轮直径，砂轮厚度、毛坯直径等参数，系统会自动计算并在G代码中添加工步间的进退刀代码(G代码由后置算法计算得到)。图4 为软件参数设置界面。

图4 参数设置界面

以S500T+型工具磨床为例进行算法的验证。该磨床的毛坯夹头所在转轴为A转轴，砂轮组所在转轴为C转轴，具体模型见图1b。砂轮组上安装3个砂轮，砂轮安转位置分别为：14.33mm、51.3mm和102.51mm，砂轮直径分别为：125mm、100mm和100mm，砂轮厚度分别为：6mm、6mm和36mm。对4齿铣刀进行加工，毛坯装夹长度为40mm，毛坯直径为10mm。加工过程主要包括了周齿开槽、磨端齿容屑槽、磨后刀面等工步，工步间进退刀安全阈值δ设置为10mm。图5是计算得到的第4工步和第5工步之间的进退刀代码，两个工步分别为周齿开槽和磨端齿，加工姿态差别明显。

图5 进退刀代码部分计算结果

在VERICUT7.3中按磨床实际参数建立仿真模型，载入相应的加工代码进行仿真，并在S500T+型工具磨床上进行实际加工。图6为仿真中安全位置和快速逼近位置，可以看出工步间的快速进退刀位置合理安全，保证砂轮和毛坯之间不会发生碰撞。图7为实际加工结果，结果显示整体加工完整，没有干涉现象。

(a)安全位置 (b)快速逼近位置图6 安全位置和快速逼近位置

图7 实际加工结果

6 结束语

(1)分析了磨床结构与工步间进退刀方式的关系，定义了砂轮毛坯干涉检测坐标系，并以此为基础提出一种不同结构磨床进退刀位置的统一计算方法，提高了方法的通用性。

(2)提出一种干涉检测坐标系和机床坐标系相互变换的求解方法，求解出安全位置和快速逼近位置坐标，并用投影法来简化计算，提高了方法的高效性。

(3)设计了一套立铣刀加工进退刀处理软件，并进行了仿真和实际加工验证，结果显示了方法的可靠性和软件较高的自动化水平。

[参考文献]

[1] 罗伯勋. 磨削S形刃球型立铣刀前刀面之数学模型[J]. 应用数学, 1988(1):85-92.

[2] Yuan Ning,M Rahman,Y S Wong. Investigation of Chip Formation in High Speed End Milling[J]. Journal of Materi-als Processing Technology, 2001,113(1):360-367.

[3] Yoong-Ho Jung, Jeong-Suk Kim, Sang-Moon Hwang. Chip Load Prediction in Ball-end Milling[J]. Journal of Materials Processing Technology, 2001, 111(1):250-255.

[4] Shangjian Du, Tobias Surmann, Oliver Webber, et al. Formulating Swept Profiles for Five-Axis Tool Motions[J]. International Journal of Machine Tools and Manufacture, 2005, 45 (7):849-861.

[5] 刘井玉, 蒲红, 胡晓平. 特种回转面刀具五联动数控磨削后处理算法[J]. 佳木斯大学学报(自然科学版), 2002, 20(3):264-267.

[6] 李长映. 数控刀具磨床加工整体硬质合金球头立铣刀的研究[J]. 中国新技术新产品, 2016(8):99-100.

[7] 汪羿, 何彪, 马辉,等. 新型球头立铣刀刃磨加工研究(Ⅰ)[J]. 贵州工业大学学报:自然科学版, 2004, 33(5):96-98.

[8] 范运金. 五轴数控工具磨床加工后球头刃铣刀的软件拓展[J]. 工具技术, 2011, 45(4):79-80.

[9] 刘建军, 黎荣, 程雪锋,等. 圆弧头立铣刀端刃CNC磨削仿真技术研究[J]. 现代制造工程, 2012(10):84-89.

[10] 刘慧, 郑飂默, 杜少华. 五轴侧铣刀具半径补偿路径优化技术的研究[J]. 组合机床与自动化加工技术, 2014(10):36-39.