基于非线性PID的交叉耦合同步控制器设计*

盛贤君，张亚鹏，许 才

(大连理工大学 电气工程学院，辽宁 大连 116024)

0 引言

在数控机床加工制造设备中，常要求双轴进行同步运动，如龙门机床的两平行进给轴、镜像加工装备加工主轴与支撑轴等[1-2]。理想情况下，双轴通过跟踪运动指令实现协调同步；但机床实际运动过程中，由于扰动、伺服参数不匹配等影响，导致单轴伺服响应存在延时产生跟踪误差，双轴运动不协调产生同步误差[3]。为了减小同步误差，一方面需要降低单轴的跟踪误差，提高单轴的跟踪精度，另一方面还需要引入交叉耦合控制，以实现双轴的协调同步。

数控机床的位置控制是控制输出量的最后环节，直接影响最后的加工质量，位置控制的优劣决定系统跟踪精度的高低[4]。传统的位置伺服控制系统通常采用PID控制方法，但存在控制参数适应性差、抗干扰能力不强等缺陷[5-7]。为了适应机床精确的运动需要，提高位置伺服系统的跟踪精度、抗干扰性，采用非线性PID的位置控制，其架构简单、控制性能较好。文献[8-9]设计的非线性函数的位置PID控制器实现超调量小、抗干扰性强，但系统上升时间慢于PID控制。文献[10]设计的非线性PID控制器改善了伺服控制系统的动静态性能，但控制器参数整定较为复杂。针对以上不足，采用非线性PID的位置控制器，并通过遗传算法进行离线参数寻优，减小跟踪误差。

交叉耦合同步控制由美国密歇根大学Y Koren等首先提出[11]，其核心思想是在并行同步控制的基础上加入轴间耦合作用，将轴间同步误差引入交叉耦合控制器(CCC控制器)中，经过CCC控制器内控制算法进行处理后，以附加信号的形式分别分配至两轴，对轴间误差进行补偿，从而能够获得较好的同步控制性能[12]。文献[13-14]通过分析轮廓误差与跟踪误差的关系设计变增益交叉耦合控制有效降低轮廓误差。文献[15]通过设计交叉耦合算法能够有效降低机床双驱间的同步控制误差。

本文将对经典的位置控制策略和直线型双轴同步运动的同步误差与跟踪误差几何关系进行分析，并引入耦合误差变量，提出一种位置环非线性PID的交叉耦合同步控制器，以实现跟踪精度和同步性的同时提高。

1 伺服系统位置控制器

1.1 传统线性PID控制器

传统PID控制器是将控制偏差的比例、积分、微分线性组合构成控制量来控制被控对象。其控制表达式为：

(1)

式中，u(t)为控制器的输出；e(t)为控制器的输入，即偏差信号；Kp为比例系数；Ki为积分系数；Kd为微分系数。

传统PID控制算法对于系统参数变化或设定值跟踪与抑制扰动采用线性算法进行优化，很难真实地反映控制量与偏差信号之间的非线性关系，使系统不能获得较佳的控制效果。为了取得更好的控制效果，准确地反映控制量与偏差信号之间的非线性关系，采用非线性PID控制算法对系统参数变化进行跟踪。

1.2 非线性PID控制器

根据PID控制原理，非线性PID控制器的比例函数、积分函数、微分函数的构造思想为：

(1)比例函数Kp(e)：比例控制主要是获得较小的超调量，加快系统响应速度。当系数输出在远离期望值时，Kp(e)的绝对值应该较大，而在期望值附近时，Kp(e)的绝对值应该很小，因此构造非线性比例函数为：

(2)

式中，ap，bp，cp为正实数，且为定值；当误差e趋近于无穷大时，比例增益系数Kp取最大值an+bn，当误差e趋近于0时，比例增益系数Kp取最小值ap。cp的值决定Kp的变化速度。

(2)积分函数Ki(e)：积分控制主要是消除系统的稳态误差。当系统误差较小时，Ki(e)应取较大的值，当误差较大时，Ki(e)应取较小的值，这样保证控制系统静态无误差，加快系统响应速度，又不会引起积分饱和而使超调增大，因此构造非线性积分函数为：

(3)

式中，ai，bi为正实数；当误差e趋近于无穷大时，Ki应取最小值0，当误差e趋近于0时，Ki应取最大值ai。bi的值决定Ki的变化速度。

(3)微分函数Kd(e)：微分控制主要是加快系统稳态调节速度，增加系统阻尼，减小调节时间。对于微分作用在位置控制模式来说，不应该取较大值，主要是因为位置环是最外环，响应时间比较长，系统本身也有了一定的阻尼，如果微分作用较大，很容易导致系统不稳定，甚至发生振荡。微分作用控制较为简单，即与偏差的变化趋势相反即可，因此构造非线性微分函数为：

(4)

式中,ad，bd，cd，dd为正实数；当误差e趋近于正无穷大时，Kd应取最小值ad，当误差e趋近于负无穷大时，Kd应取最大值ad+bd，当误差e趋近于0时，Kd应取值为ad+bd/(1+cd)。dd的值决定Kd的变化速度。

由上述可知非线性PID控制器的函数表达式：

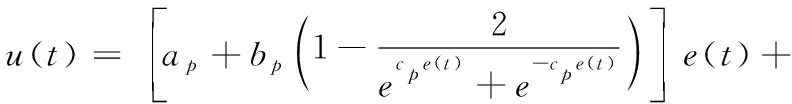
(5)

式中，u(t)为非线性PID控制器的输出。

2 双轴伺服系统同步控制器设计

2.1 同步误差与跟踪误差的几何关系

研究双轴同步控制须关注的2个指标：跟踪误差和同步误差，设计同步控制系统目的是使这2个指标尽可能快地收敛为零，定义X、Y轴的跟踪误差ex/y为：

ex=pxd-pxa
ey=pyd-pya

(6)

定义同步误差eps为：

eps=px-py

(7)

式中，px、py表示X、Y轴实际位移。

双轴同步误差与跟踪误差的几何关系如图1所示，OD为理论双轴运动轨迹；OA为实际双轴运动轨迹；45°为理论轨迹与X轴夹角；Pd(pxd，pyd)为期望位置点；Pa(pxa，pyd)为实际位置点；e为跟踪误差；eps为同步误差。

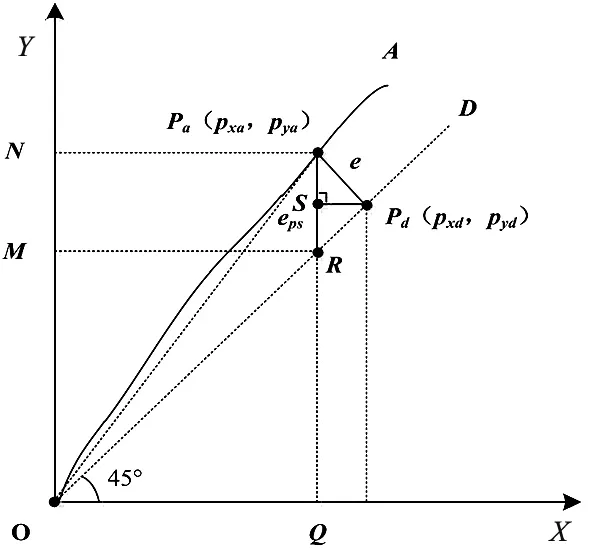
图1 同步误差与跟踪误差几何关系

(8)

则同步误差与跟踪误差的几何关系为：

eps=ex-ey

(9)

为提高单轴跟踪精度和实现双轴同步运动，即要求ex、ey和eps都尽快地收敛为0，因此提出改进的交叉耦合同步控制策略。

2.2 双轴同步控制器设计

双轴控制器不仅要求保证单轴的位置跟踪精度，还要消除轴间的同步误差，因此引入耦合误差e*，其包含了各轴的跟踪误差和同步误差，耦合误差公式为：

(10)

式中，β为耦合系数，表示同步误差项在耦合误差中的权重，用于衡量控制系统的跟踪性能和同步性能。耦合误差e*作为位置控制器的输入，任意轴位置控制器对双轴的跟踪误差都做出反应，以提高跟踪精度和双轴同步性。

根据传统交叉耦合控制，结合式(10)设计双轴同步控制系统结构如图2所示，图中pxd和pyd是运动控制器的参考位置指令；pxa和pya是X、Y轴电机实际位置；eps是同步误差；β是耦合系数；cx和cy是交叉耦合控制器的同步误差分配系数；Gx和Gy是X、Y轴包括速度环、电流环和执行机构在内的环节；Gpx和Gpy是X、Y轴位置控制器，采用非线性PID控制算法；Gc是交叉耦合控制器，采用PD控制算法，以提高系统稳定性和响应速度。原理为：包含跟踪误差ex/y和同步误差eps的耦合误差e*作为位置控制器的输入，建立两轴的耦合关系，同时减小跟踪误差和同步误差，提高跟踪精度和双轴同步性；同步误差eps为交叉耦合控制器的输入，处理获得两轴同步误差补偿控制量，将补偿量叠加到各伺服轴，以实现双轴同步运动。

图2 双轴同步控制结构框图

3 实验验证

3.1 实验平台

采用X-Y运动平台验证提出的位置环控制结合交叉耦合控制的有效性，如图3所示。X-Y运动平台选用了日本THK公司生产的十字滑台AX1015P4EY，X轴有效行程为150mm，Y轴有效行程为100mm，重复定位精度±0.001mm，螺距5mm。所用伺服设备是日本松下公司的MINAS A5 II系列伺服驱动器及电机。

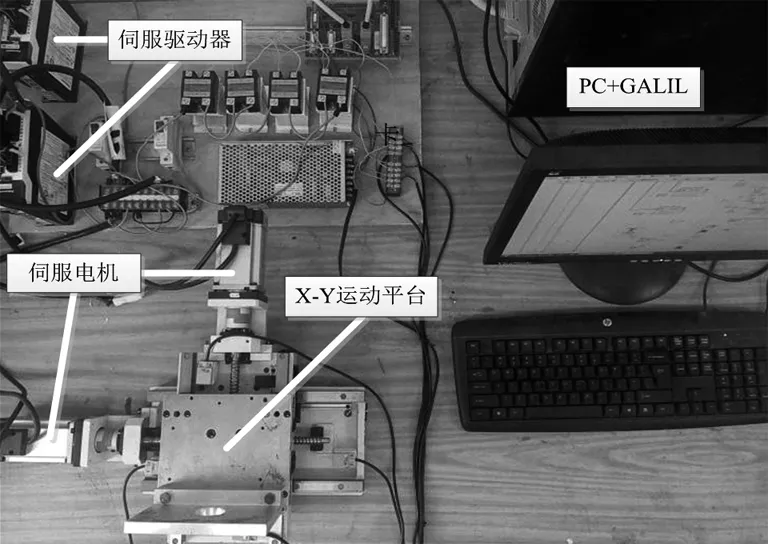
图3 X-Y运动平台

系统中每个伺服轴均为三环串级控制结构如图4所示，伺服电机编码器作为位置环传感器将信号反馈至伺服驱动器及运动控制器中，构成半闭环控制；速度环和电流环PID控制器内置于伺服驱动器中。位置环和交叉耦合结构在LabVIEW平台上完成，设计原理为：使用GALIL卡TP指令进行平台位置的反馈，通过反馈的位置指令计算出X轴和Y轴各自的跟踪误差，两轴跟踪误差求差得到轴间同步误差。由跟踪误差和同步误差得到耦合误差，其值作为位置环非线性PID控制器的输入，经过非线性函数处理将最终参数修改指令至GALIL卡；同步误差经过PD控制器处理后分别乘以各轴的同步系数，再以速度补偿的形式对各轴的速度值进行修改。

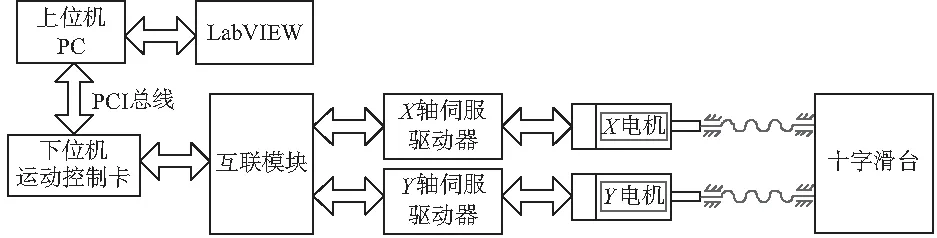
图4 系统总体结构

3.2 对比实验及分析

为验证位置环非线性PID的交叉耦合同步控制器的有效性，采用X-Y运动平台分别进行PID+传统交叉耦合、非线性PID+传统交叉耦合、非线性PID+改进的交叉耦合同步控制对比实验。Gc交叉耦合控制器采用PD控制器，其参数为：Kpc=100、Kdc=40；同步误差分配系数cx=1、cy=1；耦合系数β=1.5；位置环为PID控制器时参数为：Kpx=15、Kpy=15，Kix=0.5、Kiy=0.5，Kdx=50、Kdy=50；位置环为非线性PID控制器时参数如表1所示。三组实验的运动行程PR均为10mm，电机初始速度SP均为0.5mm/s，实验的主要评价指标为系统单轴跟踪误差及轴间同步误差。

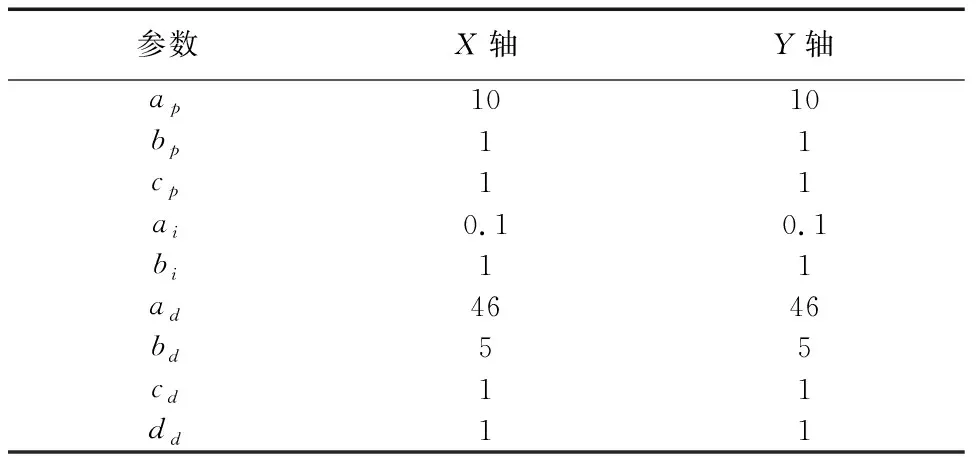
表1 非线性PID参数

图5a、图5b、图5c分别为PID+传统交叉耦合(方法Ⅰ)、非线性PID+传统交叉耦合(方法Ⅱ)、非线性PID+改进的交叉耦合(方法Ⅲ)三种情况下的X轴跟踪误差、Y轴跟踪误差和轴间同步误差实验曲线，表2～表4分别为X轴跟踪误差、Y轴跟踪误差和轴间同步误差的最大值、均方根值。

(a) X轴间跟踪误差

(b) Y轴间跟踪误差

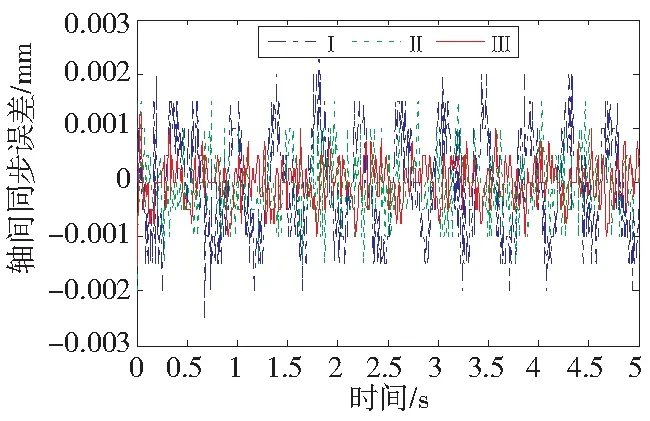
(c) 轴间同步误差图5 轴间同步误差、X和Y轴跟踪误差

实验条件X轴跟踪误差(mm)最大值均方根值PID+交叉耦合0.00200.0008非线性PID+交叉耦合0.00150.0007非线性PID+改进的交叉耦合0.00100.0003

表3 Y轴跟踪误差

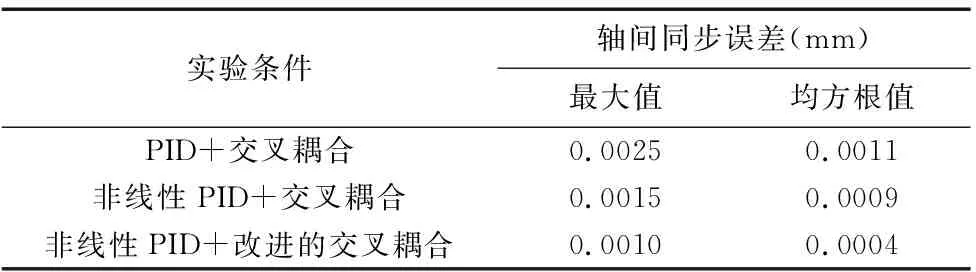
表4 轴间同步误差

由图5实验曲线可以明显看出，在相同条件下，采用非线性PID+改进交叉耦合的控制策略最佳，能够提高系统的跟踪性能，并且有效的减小轴间同步误差。由表2～表4可知，非线性PID+改进的交叉耦合同步控制相比于非线性PID+传统交叉耦合同步控制，在X轴跟踪误差的最大值和均方根值上分别减少了33.33%和57.14%，在Y轴跟踪误差的最大值和均方根值上分别减小了33.33%和50%，在轴间同步误差的最大值和均方根值上分别减小了33.33%和55.56%。非线性PID+改进的交叉耦合同步控制相比于PID+传统交叉耦合同步控制，在X轴跟踪误差的最大值和均方根值上分别减少了50%和62.5%，在Y轴跟踪误差的最大值和均方根值上分别减小了50%和55.56%，在轴间同步误差的最大值和均方根值上分别减小了60%和63.64%。可见，在非线性PID的改进的交叉耦合同步控制下，明显提高了跟踪精度和同步性。

4 结论

本文在分析了经典的位置控制策略和双轴同步运动的同步误差与跟踪误差几何关系的基础上，并引入耦合误差变量，设计了一种位置环非线性PID控制结合改进的交叉耦合的双轴同步控制器，利用X-Y运动平台进行双轴同步控制实验。结果表明：非线性PID+改进的交叉耦合同步控制相比于PID+传统交叉耦合同步控制，在X轴跟踪误差的最大值和均方根值上分别减少了50%和62.5%，在Y轴跟踪误差的最大值和均方根值上分别减小了50%和55.56%，在轴间同步误差的最大值和均方根值上分别减小了60%和63.64%。根据实验结果可知，位置环非线性PID控制结合改进的交叉耦合的双轴同步控制器减小了双轴不协调引起的误差，提高了双轴的同步性。本文提出的同步控制器也可推广到机床加工装备多轴同步控制平台，以提高各轴的跟踪精度和多轴的同步性。

[参考文献]

[1] 黄亮. 大型数控滚齿机伺服系统同步控制研究[D]. 重庆:重庆大学,2011.

[2] 谢敏.大型薄壁构件镜像加工装备数控系统设计[D]. 大连:大连理工大学,2016.

[3] Huo F, Poo A N. Precision contouring control of machine tools[J]. The International Journal of Advanced Manufacturing Technology,2013, 64(1):319-333.

[4] 王德斌. 运动控制系统及其在机床数控化改造中的应用与研究[D]. 上海:上海交通大学,2007.

[5] Kishor N, Singh S P, Raghuvanshi A S, et al. Comparative performance study of QN and LM algorithms in predictive control for NNARX-identified model of hydro-power plant[J]. Engineering with Computers, 2007, 23(2):71-78.

[6] 张营，李鹏，周珂,等. 回推非线性PID复合控制在伺服系统中的应用[J]. 组合机床与自动化加工技术，2012(5)：41-44.

[7] Prakash J, Srinivasan K. Design of nonlinear PID controller and nonlinear model predictive controller for a continuous stirred tank reactor[J]. Isa Transactions, 2009, 48(3):273-282.

[8] 彭振洲. 直线电机驱动的数控机床XY工作台轮廓误差控制系统设计[D]. 成都:电子科技大学, 2013.

[9] 申永. 数控位置跟踪中非线性PID位置控制器的研究[D]. 济南:山东理工大学, 2012.

[10] 田乃强. 二维精密运动平台的轮廓伺服控制器设计[D].哈尔滨:哈尔滨工业大学,2015.

[11] Y Koren. Cross-coupled biaxial computer control for manufacturing systems[J]. Trans. ASME J. Dyn. Syst. Meas. Control., 1980,102 (4):265-272.

[12] J Yang, Z Li. A novel contour error estimation for position loop-based cross-coupled control[J]. IEEE-ASME Trans.Mechatron, 2011,16(4):643-655.

[13] 许强强，曾岳南. 两轴变增益交叉耦合控制系统的仿真分析[J]. 组合机床与自动化加工技术，2010(12)：80-82.

[14] 赵为志. 基于交叉耦合的双自由度平台协同控制[D]. 哈尔滨:哈尔滨工业大学, 2016.

[15] 陈海森, 张德新, 王继河,等. 基于H_∞-交叉耦合算法的双驱同步控制[J]. 浙江大学学报(工学版), 2017, 51(1):131-137.