基于GA-Newton法的异步电机改进模型参数辨识*

孟庆硕，许鸣珠

(石家庄铁道大学 机械工程学院,石家庄 050043)

0 引言

异步电机可靠性好、性能优良、制造简单、瞬时转矩高，并且高性能的永磁同步电机受限于制造工艺的影响，在一些特殊场合异步电机正在逐渐的取代同步电机，因此异步电机控制得以快速发展[1-2]。实现高性能的异步电机控制，其关键问题是如何准确的获得电机的参数。在电机运行过程中，电机参数往往易受温度、定子电流和磁链饱和等多重因素的影响，使得矢量控制、直接转矩控制等一系列控制方法难以达到预期的效果。因此，各种参数辨识方法成为了研究热点，如：文献[3-4]基于扩展卡尔曼滤波器(EKF)的参数辨识方法，此种方法需要对4阶矩阵进行求逆运算，计算量大，并且初始估计误差协方差P、系统噪声协方差Q和测量噪声协方差R较难确定，对系统估算精度和收敛速度有着较大的影响。文献[5-6]采用基于最小二乘(RLS)的参数辨识方法，其对测量噪声的鲁棒性较差，同时易受转速波动的影响。文献[7-8]采用基于模型参考自适应(MRAS)的参数辨识方法，具有较好的跟踪收敛特性，但当辨识参数增加时，自适应率的选取较为困难。

针对以上参数辨识算法存在的缺点，有学者将一种模拟生物进化进行全局最优搜索的算法-遗传算法(GA)[9]引入到参数辨识中。如：文献[10]基于遗传算法的内埋式永磁同步电机参数辨识方法，证明了该方法在参数辨识方面的可行性，并且具有较高的准确性。

在异步电机参数辨识中，往往需要对电机静止α-β坐标系电流项进行二次求导，才能构建电机的辨识模型，这样既增加了计算量，同时也引入了更多的噪声。并且此种模型还需要电机的定转子磁链作为输入，而磁链往往不易直接获得，需要建立复杂的磁链观测器模型。本文在电流定向1-2坐标系下推导出电机的转子磁链，与α-β坐标系电流一阶导数模型结合即可得到改进的辨识模型。该模型只需要定子电压和定子电流这些可直接观测的状态变量，易于操作。又将牛顿法与遗传算法结合，牛顿法能够加速种群朝着最优解的方向进化，从而提高遗传算法的收敛速度和寻优能力。

1 改进的异步电机辨识模型

1.1 α-β轴系电机模型

根据文献[11]，以定子电流和转子磁链为状态变量可以得到异步电机在两相静止α-β坐标系下电流一阶导数模型，如式(1)：

(1)

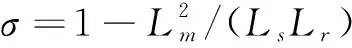
1.2 电流定向轴系下稳态磁链和定子电阻推导

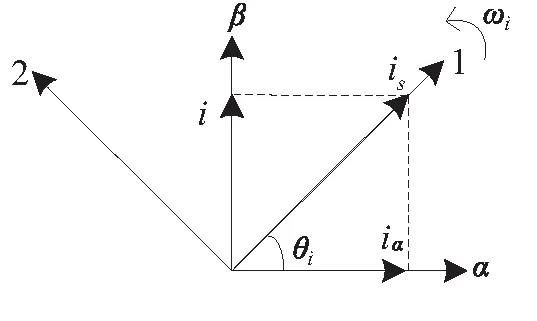
图1 电流定向的1-2坐标系

在异步电机控制中，应用较为广泛的坐标系既为静止α-β坐标系和转子磁场定向的d-q坐标系，为了利用静止α-β坐标系状态方程进行遗传算法参数辨识，就需要获得电机的转子磁链。本文引入一种基于定子电流定向[12]的新坐标系如图1所示，在该坐标系下，可以获得电机在稳态情况下的转子磁链和定子电阻。本文分别采用下标1、2来区分各矢量在1、2坐标系上的投影。

由图1可知，1-2坐标系与α-β坐标系间电流的变换关系满足式(2),同理电压和磁链也满足该变换关系。

(2)

(3)

(4)

(5)

(6)

θu(k)=arctg[uβ(k)/ua(k)]，θu∈[-π/2,π/2]

(7)

其中，ωi为坐标系同步旋转角速度。

1.3 改进后辨识模型

假设K1、K2、K3、K4可推出K5、K6，如下：

(8)

则改进后电机的辨识模型为式(9)：

(9)

其中磁链需要利用1-2坐标系到α-β坐标系的变换关系式(2)进行反变换方可代入。

2 遗传算法设计

为了将电机的数学模型式(9)转化成遗传算法的问题描述，将电机的数学模型进行离散化处理如式(10)、式(11)所示。

从自己实习的会计电算化专业选择16级、17级两个班进行一个学期的教学，学生基础知识较差，实践动手能力较强，活泼、好动，适用于该教学法。两个班的具体情况见表1。

(10)

(11)

(12)

由电流定向可以求得定子电阻，辨识算法也可以求得定子电阻，因此增加了辨识算法的约束条件，根据(12)式和(10)式和(6)式可以建立系统的目标函数(13)式：

(13)

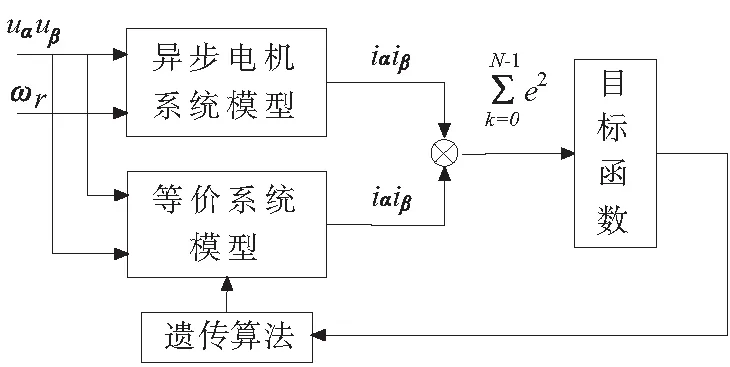
图2 遗传算法原理图

3 GA-Newton辨识原理

在利用遗传算法对系统进行参数辨识时，常遇到系统收敛速度慢，“早熟”等现象。为了求取全局最优个体，扩大种群的搜索能力，提高种群的收敛速度，本文引入了Newton法。

(14)

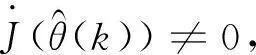
4 GA-Newton辨识算法设计

(1)编码方式及初始种群选取

4个参数均采用二进制编码，编码长度均为10位，编码精度为0.001。种群容量30，每个个体都由计算机随机产生。

(2)适应度函数选取

(15)

(3)选择操作

采用轮盘赌选择的方法，传统的遗传算法中适应度函数越大，个体的存活几率越大。本文依据的是适应度越小，生存几率越大，因此对个体的适应度取倒数以满足轮盘赌操作。为避免个体的交叉和变异破坏已达到全局最优解的个体，采用精英保留法。

(4)Newton法迭代

利用Newton法对个体进行一次迭代，并加入到子代个体中。

(5)交叉操作

为了增大系统的搜索范围采用多点交叉和自适应交叉率，如下：

(16)

式中,Pc1=0.9；Pc2=0.6；Favg为种群的平均适应度；Fmin为种群中个体最小适应度；F′为交叉的两个个体中较小的适应度。

(6)变异操作

采用单点变异和自适应变异率，如下：

(17)

式中，Pm1=0.1；Pm2=0.01；F′为变异个体的适应度。

5 实验结果

异步电机参数辨识结构框图如图3所示，电机采用双闭环矢量控制。采用TI公司的TMS320F2812 DSP芯片来实现辨识算法， 试验用异步电机额定参数为：Pn=250W；Un=36V；In=9A；ωn=1400r/min；极对数P=2。DSP系统时钟为150MHz，PWM信号调制频率为15kHz。采用IR2110驱动芯片和高达25A、1200V的IGBT管组成。PWM驱动信号通过高速光耦完全隔离高压与低压侧，保证驱动板不受高压干扰。电压信号采样通过测试母线电压，利用电压重构技术得到A、B、C相电压。电流信号采样采用霍尔传感器对其进行测量。信号采样频率T=15kHz，速度通道一阶低通滤波器截止频率10Hz。电压和电流通道均为二阶巴特沃兹低通滤波器，截止频率分别为10Hz。遗传算法最大进化代数为1000。

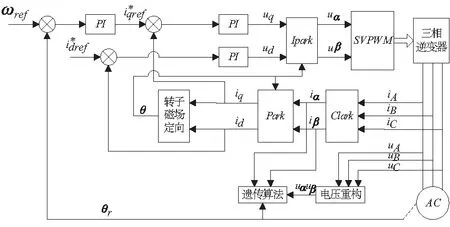
图3 异步电机参数辨识结构框图

对比图4和图5可知经典遗传算法，系统收敛慢，系统大范围波动，得到的值往往并非系统的全局最优点。而GA-Netwon法系统收敛速度快在第5代左右便出现了系统的最优个体，并对其进行了优化，使得辨识结果更加准确。

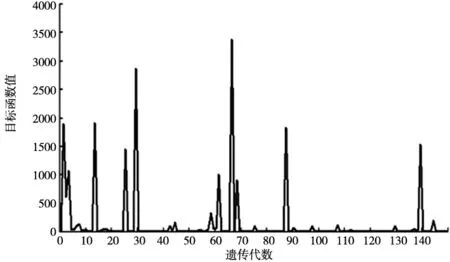
图4 经典遗传算法目标函数值

图5 GA-Netwon算法目标函数值

在转速为1400r/min 无负载的情况下，GA-Netwon算法的辨识实验结果如图6～图10所示。由于每次辨识的初始值都是计算机随机产生的，最后的辨识结果都能收敛到参照值附近见表1。从辨识结果可以看出，待辨识参数的初始值虽然远离真实值，但目标函数可以很快的收敛到零附近，待辨识的5个参数都能收敛到参照值附近，每个参数误差都在4%之内，辨识结果准确，对于电机运行控制来说已有足够的精度。

图6 定子电阻辨识过程曲线

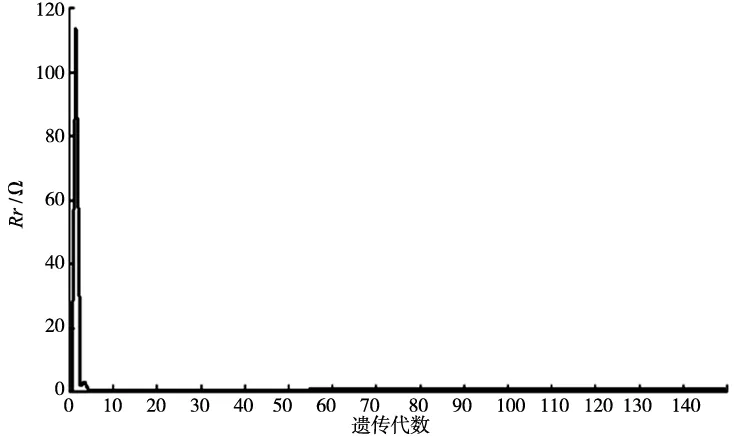
图7 转子电阻辨识过程曲线

图8 互感辨识过程曲线

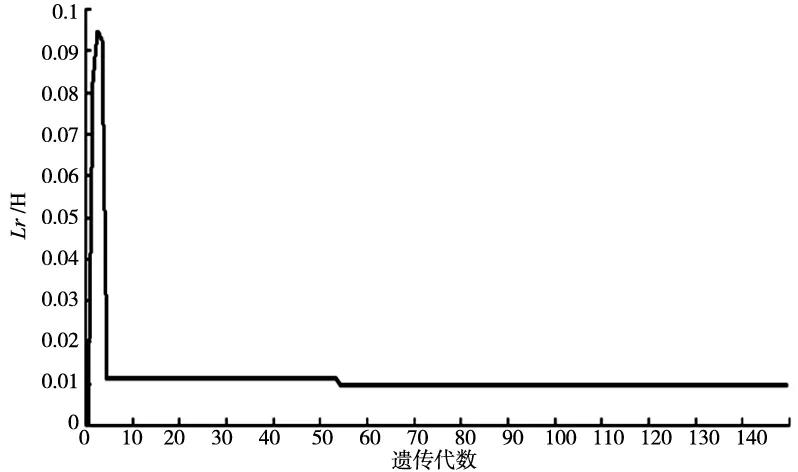
图9 定、转子电感辨识过程曲线

图10 磁链辨识过程曲线

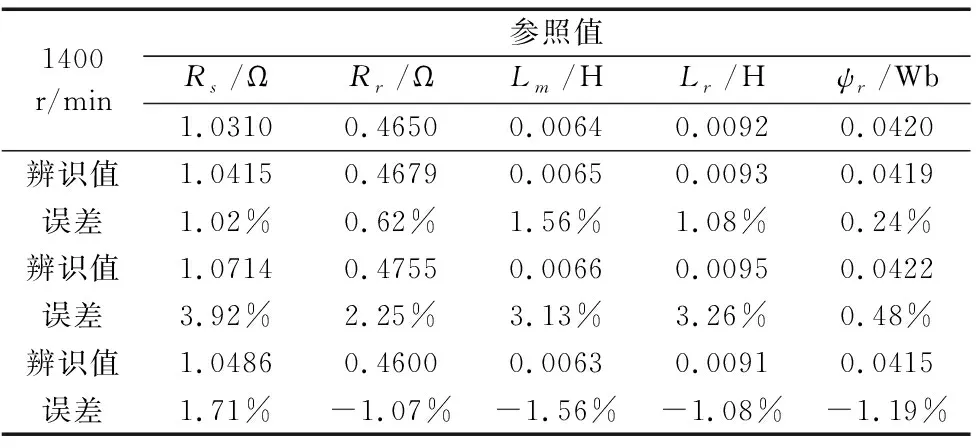
1400r/min参照值Rs/ΩRr/ΩLm/HLr/Hψr/Wb1.03100.46500.00640.00920.0420辨识值1.04150.46790.00650.00930.0419误差1.02%0.62%1.56%1.08%0.24%辨识值1.07140.47550.00660.00950.0422误差3.92%2.25%3.13%3.26%0.48%辨识值1.04860.46000.00630.00910.0415误差1.71%-1.07%-1.56%-1.08%-1.19%

6 结论

本文在电流定向1-2坐标系下求得电机的转子磁链模型，结合静止α-β坐标系下的电机一阶导数模型，建立了可以用于GA-Netwon算法的辨识模型。实验结果表明该方法，不受初始值影响，克服了传统遗传算法对待辨识参数初始值要求高的缺点。待辨识的电机参数均能够在较短的时间内收敛到参照值，并具有较高的辨识精度，算法的鲁棒性也很好。

[参考文献]

[1] 夏超英.交直流传动系统的自适应控制[M].北京:机械工业出版社,2001.

[2] 王成元,周美文,郭庆鼎.矢量控制交流伺服驱动电动机 [M].北京:机械工业出版社,1995.

[3] 周熙炜.基于扩展卡尔曼滤波算法的异步电机参数辨识[D].西安:西安理工大学,2003.

[4] Wang S, Dinavahi V, Xiao J. Multi-rate real-time model-based parameter estimation and state identification for induction motorsv[J].Iet Electric Power Applications(S1751-8660), 2013,7(1):77-86.

[5] 张虎,李正熙,童朝南.基于递推最小二乘算法的感应电动机参数离线辨识[J].中国电机工程学报,2011,18(31):79-86.

[6] He Y, Wang Y, Feng Y, et al. Parameter Identification of an Induction Machine at Standstill Using the Vector Constructing Method[J].IEEE Transactions on Power Electronics (S0885-8993),2012,27(2):905-915.

[7] 吴锦宇.基于模型参考自适应的感应电机参数辨识技术研究[D].哈尔滨:哈尔滨工业大学,2013.

[8] 周霞.基于模型参考自适应系统的异步电机参数辨识的研究[D].杭州:浙江大学,2011.

[9] 国珍.改进遗传算法在无刷直流电机调速系统PID参数优化中的应用[J].组合机床与自动化加工技术,2013(7):90-91.

[10] 肖曦,许青松,王雅婷,等.基于遗传算法的内埋式永磁同步电机参数辨识方法[J].电工技术学报,2014,29(3):21-26.

[11] 王成元.现代电机控制技术[M].北京:机械工业出版社,2008.

[12] 张春朋,林飞,陈寿孙.改进U-I法异步电机转子磁链估计器[J].中国电机工程学报,2004,24(5):126-129.

[13] 李庆扬.数值分析[M].武汉:华中科技大学出版社,2006.