基于倒正态损失和满意度函数的多响应稳健设计*

崔庆安，王方成

(郑州大学 管理工程学院，郑州 450001)

0 引言

稳健设计作为持续性质量改进的一种重要支撑技术，旨在通过调整可控因子的水平组合来减少噪声因子对产品或质量的影响，从而实现减小整个系统波动的目的，生产出响应达到目标值且标准差较小的产品[1-2]。随着产品复杂化程度的加剧，在实际的生产制造过程中，往往需要考虑多个质量特性，因此多响应稳健参数设计在持续性质量改进过程中具有越来越重要的理论价值和实际意义[3]。

关于多响应稳健设计，国内外一些学者做了大量的研究，研究内容如下：杨方等[4]采用满意度函数法将多响应问题转化为单响应问题,由于该方法仅构建了均值满意度和标准差满意度,未考虑均值和标准差之间的相互作用,因此采用该方法算出的结果往往较不理想。多元损失函数[5]和主成分分析法，虽然可以很好地解决响应之间的相关性，但却不能解决自变量之间的相关性。何桢等[6]提出了改进的主成分分析法来解决多响应问题，该方法同时考虑优化均值和标准差，提高了过程的稳健性。伍建军等[7]将熵权理论和满意度函数法引入双响应曲面法提出了改进满意度函数的双响应稳健设计优化方法，虽然该方法可以得到稳健性的优化值，但是该方法是分别建立均值模型和标准差模型，忽略了它们之间的相互作用。罗孟然等[8]将神经网络和响应曲面法相结合提出对响应进行优化的新方法，并通过数控机床床鞍尺寸实例进行验证，显著提高了零件的质量水平。伍建军等[9]将田口方法和灰色关联法相结合建立了多响应稳健设计，通过对柔顺平行四杆机构的优化得到了更具稳健性的尺寸。

以上方法在解决多响应问题时，分别对均值和标准差进行优化，但是较少考虑二者之间的交互作用和相互影响。Koksoy和Fan[10]提出的倒正态损失函数在解决单个响应问题时，可同时兼顾均值和标准差，但较少考虑多响应情况。传统的满意度函数在解决多响应问题时较多考虑均值之间的相互作用，很少考虑均值和标准差的交互作用和相互影响。因此若采用倒正态损失函数作为中间变量改进传统的满意度函数，则可实现兼顾均值和标准差的多响应稳健优化问题。基于此，本文将倒正态损失引入满意度函数中，构造同时考虑均值和标准差的新的稳健性度量指标，并以此为基础构建响应曲面模型，进而转化为满意度函数并对其进行寻优，以解决多响应稳健参数设计问题。

1 理论简介

1.1 倒正态损失函数

(1)

其中，y是质量特征值(响应)，K是最大损失值(通常取1)，τ是过程的目标值，σL是形状参数。

倒正态损失函数是一个对称、有界的损失函数，它是一条光滑的曲线，当特征值等于目标值时，其值为0，随着特征值偏离目标值其值逐渐增大至最大损失值1，而不像田口损失函数那样增大到一个不切实际的值。形状参数σL的大小可以调整系统允许的界限，也即是一个大的σL的值暗示系统可以接受更大的偏离目标值的界限。如图1所示，我们取K=1，τ=0时不同的σL对应的损失函数。

图1 不同的σL对应的损失函数

我们从图中可以看到，σL的值越小，则系统所能接受的界限范围越小。

为了考虑整个过程的平均损失，Spiring又引入了期望损失值E[LUDN(y)],其表达式如公式(2)所示：

(2)

从公式(2)中，我们可以知道损失值和两个变量有关，一个是质量特征值偏离目标值的大小；另一个是标准差的大小，而且此公式给出了一个令人信服的事实，随着方差的增大，损失值也增大。此公式很好地表达了稳健参数设计的实质，即保证产品或响应的均值尽可能地达到设计目标值的基础上最大限度地减少响应围绕设计目标值的波动(响应方差)。假如令σL=1，τ=0，K=1，我们可以得到E[LUDN(y)]与μR,σR的图像如图2所示。

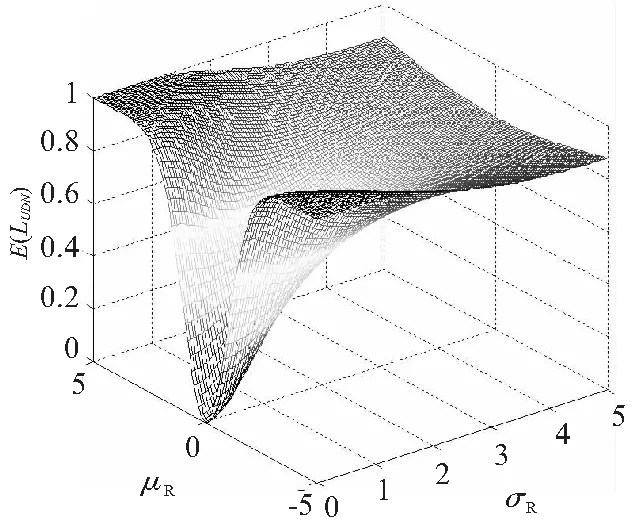
图2 E[LUDN(y)]与μR,σR的关系图

该损失函数还有一大优点，当质量特征值y不服从正态分布时，如均匀分布、指数分布、Γ分布等其损失函数仍可以求出。

尽管新的损失函数应用很多领域，如Leung和Spiring[12]应用于货币评估，Cudney和David Drain[13]应用于微控制器产品的制造过程。但他们并没有指出如何将新的损失函数运用到多响应稳健参数设计中，因此本文以此为突破口，将倒正态损失函数引入稳健参数设计中，以期望损失值作为新的稳健性度量指标建立新的响应曲面。

1.2 满意度函数法

满意度函数法是最早由Harrington[14]提出后经Derringer和Suich[15]发展起来的一种操作简单，运用广泛的多响应优化方法。该方法根据响应变量望大、望小、望目的特性将每个估计的响应变量yi转化为相应的满意度d(yi)(i=1,2,…,q)，0≤d(yi)≤1。令Ti为响应变量yi目标值，Li和Ui分别为响应变量的上下规格限。

对于望小特性的响应变量yi，其满意度函数如公式(3)所示：

(3)

从公式(3)中可以看出：对于望小特性的响应变量只有一个规格上线Ui，响应变量的值越小越好，随着响应变量值的减小，其满意度逐渐增大，当响应变量的值小于目标值时，满意度为1，大于规格上线时，满意度为0。

需要说明的是，公式(3)中的指数s或t代表了响应变量yi对于目标值得重要程度，s>1时，表明响应变量的目标值被赋予了更大的权重；相反s<1时，表明响应变量的目标值被赋予了更小的权重。

依据公式(3)建立起单个满意度函数之后，就需要一个综合的满意度函数来评价各个响应变量的水平，这里我们采用对所有单个满意度求几何平均建立综合满意度函数，如公式(4)所示：

(4)

其中,D为综合满意度函数。之所以采用几何平均来构建总体满意度，是因为几何平均有比加法平均更好的性子：当其中一个产品不能被接受时即d(yi)=0，则综合满意度D=0，整个过程或系统都不能被接受，避免了滥竽充数的可能：当其中一个满意度较低时，则综合满意度也较低，只有当所有单个响应的满意度都较高时，综合满意度才较高。目前，有较少国内外学者采用倒正态损失函数解决多响应问题。本文将采用倒正态损失函数对满意度函数进行改进，提出一种解决多响应问题的新方法。

1.3 采用倒正态损失函数改进满意度函数

传统满意度函数在解决多响应问题时，一般是分别建立均值满意度和标准差满意度，然后再把均值满意度和标准差满意度作为新的响应建立响应曲面法，进而进行优化求解。这种方法在一定程度上存在不足，当分别建立均值满意度和标准差满意度时并未考虑均值和标准差之间的相互作用，换句话说就是把均值和标准差当作独立的变量建立满意度。由标准差的公式可知，

(5)

标准差的获得是基于均值的，因此均值和标准差之间存在一定的相互作用。倒正态损失函数正是在考虑了均值和标准差的基础上建立起来的，从公式(2)中可以看出期望损失值的大小不仅与均值有关还和标准差有关。因此在建立均值满意度和标准差满意度时，可以引入倒正态损失，通过倒正态损失将均值和标准差建立在一起，考虑它们之间的相互作用，而后导入满意度函数可得公式(6)：

(6)

根据单个满意度函数，建立综合满意度，并对其进行寻优，即可实现多响应优化。

(7)

另外考虑引入倒正态损失还有一个原因是倒正态损失函数考虑了顾客的信息，传统多响应稳健设计很少考虑顾客的信息，只是从产品加工过程本身进行优化，把它当成一个纯粹的数学问题进行求解，而倒正态损失函数却和传统方法不同，它考虑了顾客的信息。顾客的信息可以决定产品偏离目标值的损失，当产品偏离规格域时，产品的制造过程将会出现很大的波动，而这一波动可以有顾客信息来减少。因此本文从顾客信息的角度，又提出了一种解决多响应问题的新思路。

2 方法步骤

针对产品设计中的多响应稳健参数设计问题，本文试图采用倒正态损失函数求出新的稳健性度量指标，通过响应曲面法建立新指标与输入变量的回归模型，并将建立起来的回归模型转化为满意度函数，对综合满意度函数进行求解，求出最佳输入因子的水平组合。具体计算过程可以分为以下几部分：

步骤1：选择恰当的实验方法

根据输入数据和输出数据的特征，选择恰当的实验方法(如中心复合设计)，并收集相关实验数据，假设系统有q个不同的响应变量yi(i=1,2,…,q)，p个可控因子xc(c=1,2,…,p)。该实验共包含n(j=1,2,…,n)个试验设计点，且在每个实验设计点上重复l(l=1,2,…,r)次实验，yijl表示第i个响应在第j个试验点重复l次实验的观测值。根据公式(8)、公式(9)求出样本的响应均值和方差。

(8)

(9)

步骤2：求出新的稳健性度量指标-期望损失值

在步骤1的基础上，根据公式(10)求出每个样本点的期望损失值。

(10)

式中，K=1，对于σL的取值在没有任何信息的情况下，Drain和Group[16]建议σL通常取响应变量可接受范围的42.5%，即σL=0.425×(Ui-Li)。

步骤3：建立响应曲面模型

根据步骤2求出来的每个样本点的期望值，建立这些期望值与输入变量的响应曲面模型，如公式(11)所示：

(11)

步骤4：求出每个响应的单个满意度函数

由于步骤2求出的期望损失值属于望小特性，因此根据公式(12)将新建立的响应曲面模型转化为望小满意度。

(12)

步骤5：建立综合满意度函数

根据步骤4求出的每个响应变量的个体满意度，按公式(13)建立综合满意度函数，并对其求取最大值获得一组最佳的输入变量的水平组合。

(13)

3 案例分析

本文根据文献[17]中提到的案例及实验数据进行分析，并与其它相关的研究方法进行对比。该案例主要研究某种胶态气体泡沫的性能问题，实验者共选取3个可控变量分别为：表面活性剂的浓度(x1)、盐水的浓度(x2)和搅拌的时间(x3)，所选择的三个变量分别为：胶质气泡的的稳定度(y1)、体积比(y2)与温度(y3)并分别为望大、望小、望目特性。该实验采用中心复合设计(CCD)收集数据，在中心点重复进行6次试验，其他点重复进行2次。具体实验数据见表1。

表1 试验数据表

对于响应均值和标准差的拟合，本文采用文献[6]的拟合模型，具体模型如下：

各个响应的质量特性不同，其规格域也不同，三个响应的规格域，如表2所示。根据响应的规格域和公式σL=0.425×(Ui-Li)可以求出每个响应对应的形状参数σ如表3所示。依据公式(10)和表3的数据求出每个样本点对应的期望损失值yLUij如表4所示。利用响应曲面法建立期望损失与三个输入变量的响应曲面模型如公式(14)～公式(16)所示：

yLU1= 0.6357-0.1886x1+0.1038x2-0.0143x3+

0.0124x1x3

R2=88.53%

(14)

yLU2= 0.5952+0.1881x1-0.0869x2+0.0744x3-

R2=88.53%

(15)

yLU3= 0.2239+0.01306x1+0.00857x2-0.02014x3+

0.00793x2x3

R2=97.70%

(16)

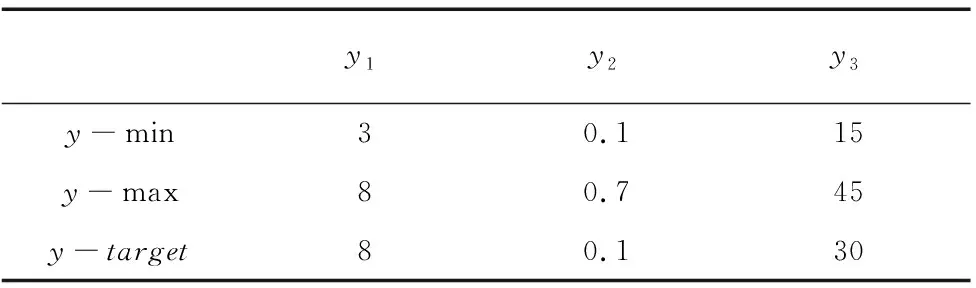
表2 响应规格域

表3 形状参数

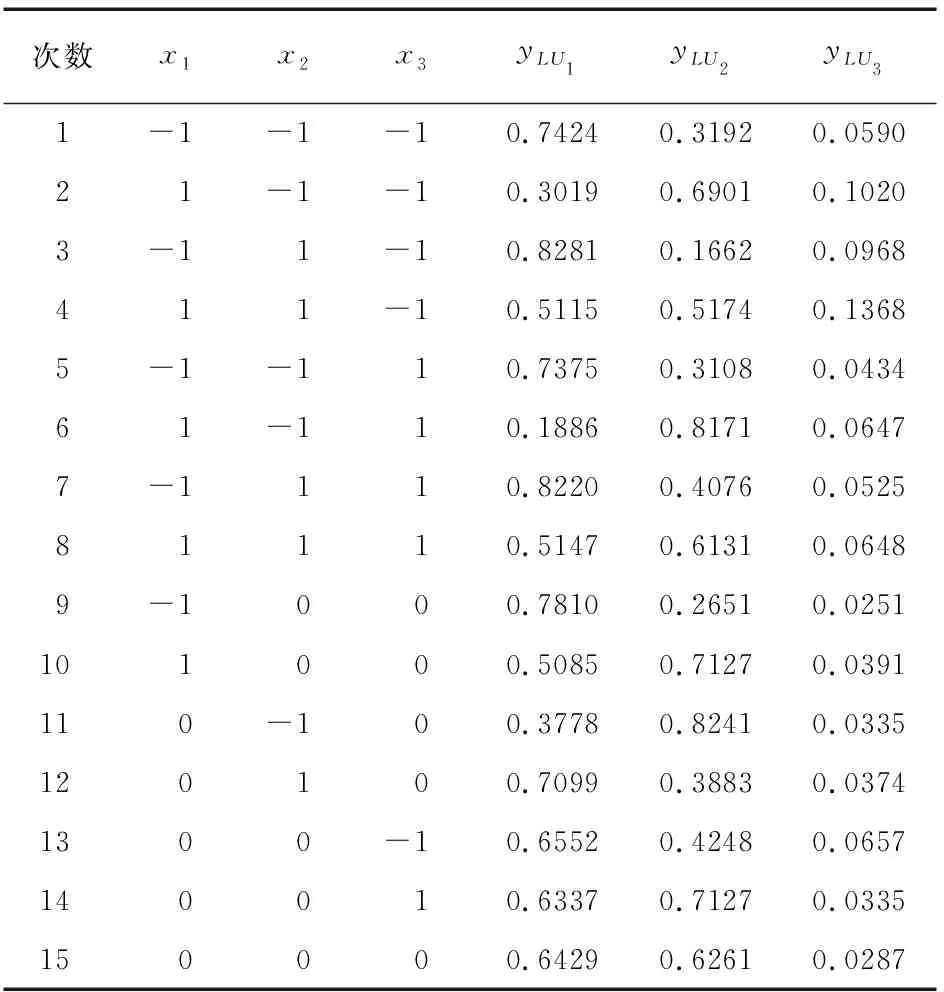
表4 期望损失值表

求出每个响应的期望损失的规格域，如表5所示。由于期望损失是望小特性，因此根据公式(9)和表5期望损失的规格域，将新建立的响应曲面模型转化为望小满意度如公式(17)～公式(19)所示：

d(yLU1)= (1-(0.6357-0.1886x1+0.1038x2-

0.0124x1x3+0.0144x2x3))/(1-0.03)

(17)

d(yLU2)= (1-(0.5952+0.1881x1-0.0869x2+

0.0273x2x3))/(1-0.2)

(18)

d(yLU3)= (0.4-(0.02239+0.01306x1+0.00857x2-

0.00618x1x3-0.00793x2x3))/(0.4)

(19)

最后根据公式(13)转化为综合满意度函数：

(20)

至此，将多响应问题转化为单响应问题，利用Matlab软件中的遗传算法工具箱对公式(20)进行寻优，得到的结果见表6(DS法是文献[15]中提出的满意度函数法；KL法是文献[17]中提出的最大最小满意度函数法；PCA法是文献[6]中提出的改进主成分分析法)。

通过对比可以看出，本文提出的方法更具有普适性和灵活性，此方法不仅充分利用了原始数据信息，而且还融入了顾客信息。表2给出了由顾客决定的响应规格域，顾客的信息决定了产品偏离目标值所带来的损失。在以往研究中，传统的稳健设计方法大多都忽略了顾客的信息，把它当成一个纯粹的数学优化问题，脱离实际。另外当响应的分布超出规格域时，此时的过程具有较高的易变性，生产出的产品将不符合要求。通过实际的数学运算可以看到，当制造商选择了严格的规格界限时，此时的产品稳定性，可靠性都较好。从表6中可以看出，本文提出的方法与DS法相比，响应y1的均值和响应y3的均值比DS法好，且标准差较小，稳健性更好；与KL法相比响应y2的均值和响应y3的均值比KL法算出的结果优；与PCA法相比响应y1的均值和响应y2的均值以及响应y3的均值都比PCA方法优，最重要的是用本文提出的方法算出的响应的标准差更小，稳健性更好，符合稳健参数设计的要求。

表5 期望损失的规格域表

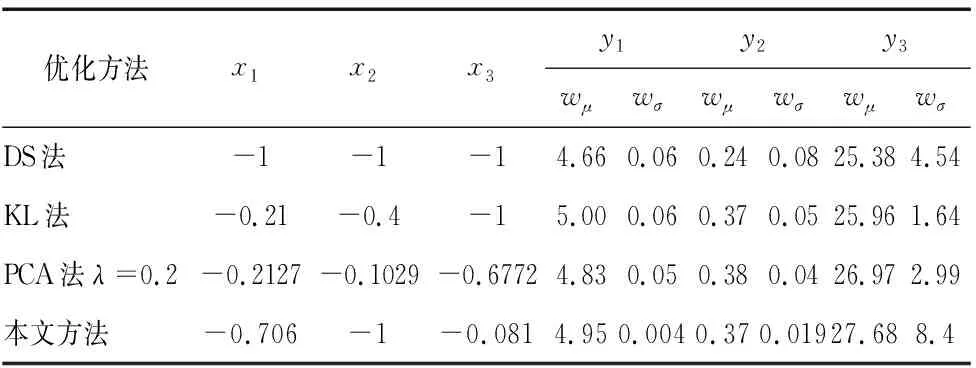
表6 各优化方法结果的对比表

4 结论

本文在响应曲面法建模的基础上，提出了一种基于倒正态损失函数和满意度函数的多响应优化方法。该方法通过引入倒正态损失函数建立了同时考虑均值和标准差的新的稳健性度量指标，克服了传统方法在建模时分别建立均值和标准差模型的缺陷，避免了均值和标准差关系的割裂，做到了在使均值接近目标值的同时标准差也较小，有效地控制了系统的波动。

[参考文献]

[1] Ouyang L, Ma Y, Byun J. An Integrative Loss Function Approach to Multi-Response Optimization[J]. Quality and Reliability Engineering International, 2015, 31(2):193-204.

[2] 何桢，张生虎，齐二石. 基于RSM和田口方法改进产品/过程质量[J]. 管理工程学报，2001,15(1):22-25.

[3] 汪建均，马义中，欧阳林寒,等. 多响应稳健参数设计的贝叶斯建模与优化[J]. 管理科学学报，2016,19(2)：85-94.

[4] 杨方, 高齐圣, 于增顺. 多响应问题的稳健性设计优化[J]. 工业工程, 2010, 13(3):43-46.

[5] 张旭涛, 何桢, 毕海玲. 基于似无关模型的改进多元损失函数方法[J]. 工业工程, 2016, 19(6):51-55.

[6] 何桢，张迎冬. 基于主成分分析的多响应稳健性优化方法研究[J].工业工程与管理，2012,17(6):47-54.

[7] 伍建军, 黄裕林, 谢周伟,等. 基于改进满意度函数法的双响应曲面稳健设计优化[J]. 机械设计与研究, 2016,32(3):1-5.

[8] 罗孟然, 丛明, 王德胜,等. 基于响应面法的数控机床床鞍尺寸优化[J]. 组合机床与自动化加工技术, 2014(9):6-9.

[9] 伍建军, 吴佳伟. 柔顺平行四杆机构多目标稳健优化设计[J]. 组合机床与自动化加工技术, 2016(5):62-66.

[10] Onur Koksoy, Shu-Kai S Fan. An upside-down normal loss function-based method for quality improvement[J]. Engineering Optimization, 2012, 44(8):935-945.

[11] Spiring F A, Yeung A S. A General Class of Loss Functions with Industrial Applications[J]. Journal of Quality Technology, 1998, 30(2):152-162.

[12] Leung B P K, Spiring F A. Some Properties of the Family of Inverted Probability Loss Functions[J]. Quality Technology & Quantitative Management, 2004, 1(1):125-146.

[13] Cudney E A, Drain D, Sharma N K. Determining the Optimum Manufacturing Target using the Inverted Normal Loss Function[J]. International Journal of Quality Engineering & Technology, 2011, 2(2):173-184.

[14] Harrington, E C. The desirability function[J].Industrial Quality Control, 1965, 21(10):494-498.

[15] Derringer G. Simultaneous Optimization of Several Response Variables[J]. Journal of Quality Technology, 1980, 12(4):214-219.

[16] Drain D, Gough A M. Applications of the upside-down normal loss function[J]. IEEE Transactions on Semiconductor Manufacturing, 1996, 9(1):143-145.

[17] Kim K J, Lin D K J. Optimization of multiple responses considering both location and dispersion effects[J]. European Journal of Operational Research, 2006, 169(1):133-145.