预条件共轭梯度法求解三维地电场有限元方程的网格分析*

王威，李景富，刘洁

（1.中山大学地球科学与工程学院∥广东省地质过程与矿产资源探查重点实验室，广东广州510275；2.广东省有色地质环境中心，广东广州510060）

直流电阻率法作为经济高效的地球物理勘探方法，在矿产资源勘探，水文地质调查，工程勘察领域获得了广泛的应用[1-6]。正演数值模拟不仅是分析特定地电结构响应特征的有效手段，而且作为反演的必要组成步骤，其求解效率直接关系到反演是否具有实用性。常用的数值模拟方法有积分方程法、有限差分法和有限元法，其中有限元法因其坚实的理论背景和灵活的模拟策略，已成为电法勘探二、三维数值模拟中广泛采用的方法[7-11]。有限元法模拟直流电阻率问题时需要求解大型线性方程组。直接解法由于矩阵分解需要占用大量的内存，一般的个人计算机难以承受。迭代算法中的预条件共轭梯度（Pre-conditioned Conjugate Gradient）法无需分解系数矩阵，可有效减少内存需求和提升计算速度，主要有不完全Cholesky共轭梯度（ICCG）算法和超松弛预条件共轭梯度（SORCG）算法。

网格剖分是有限元模拟的重要课题。规则六面体网格由于剖分简单而在直流电法有限元模拟中被广泛采用。以往研究认为ICCG算法只适合求解三维有限差分法形成的系统方程，而不适合于三维有限元方程的求解[12]。然而，这一结论的给出是基于六面体网格的。本文提出了一种新的四面体剖分方案，经过系统的网格对比分析，结果表明我们提出的网格剖分方案不仅可以使ICCG法稳定求解有限元方程，而且存储量只需采用常规六面体网格时的50%。本研究推动了三维直流电阻率法有限元模拟的发展，为其实际应用奠定了基础。

1 直流电阻率法的有限元求解

1.1 有限元方程的构建

关于二次场电位的点源三维地电场边值问题可表示为[13]：

其中σ为电导率，它与电阻率ρ互为倒数关系；Up是由背景电导率σp引起的背景电位，Us由电导率异常体σs引起的二次场电位；r是源点到测点的向量；r是源点到测点的距离；n是求解域边界的法方向；Γs、Γ∞分别是地表和计算区域剩余部分的边界。

根据变分原理，该边值问题可转换为求解泛函的极值问题：

将求解域离散为若干单元，假设每个单元内电位符合线性分布。令泛函变分为零，可得有限元方程：（具体过程可参见文献[7]）

其中有限元系数K一个稀疏对称的矩阵，与地下结构的电阻率分布有关，右端项F是与激发源分布有关的向量，Us为需要求解的各个网格结点上的二次电位值。解出Us之后加上解析方法求出的一次场电位Up即可得最终需要的总场电位U。

1.2 有限元网格分析

网格剖分是关系预条件共轭梯度法能否稳定求解的重要因素。规则六面体网格（以下简称Hex）由于其剖分简单而获得广泛应用。规则六面体网格的内部结点只与26个结点相邻（图1）。由有限元理论可知最终形成的系数矩阵K每行的非零元素最多只有27个，又由于K具有对称性，故每行只需存储14个非零元素。

图1 六面体网格的结点连接关系Fig.1 The nodes'connection of hexahedral mesh

本文提出在六面体网格基础上进行二次剖分得到四面体网格。具体方案为将每个六面体单元剖分为5个四面体单元，注意对邻接六面体单元进行的是两种不同的划分（图2）。图2（a）中单元的结点编号分别为（1，5，4，2）、（8，4，5，7）、（3，7，2，4）、（6，2，7，5）、（4，5，7，2），图2（b）中单元的结点编号分别为（1，6，3，2）、（8，3，6，7）、（4，1，8，3）、（5，8，1，6）、（1，3，6，8）。如图 3所示，这种剖分方法得到的四面体网格一半的内部结点具有18个邻接结点，另一半的内部结点具有6个邻接结点。同样，由有限元理论可知，系数矩阵平均每行只有7个非零元素需要存储（由于系数矩阵的对称性，只需存储下三角矩阵），故其存储需求约为采用六面体网格的50%。

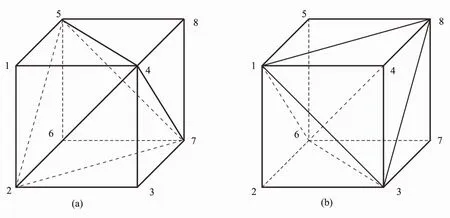
图2 在六面体网格基础上二次剖分得到的四面体网格Fig.2 The tetrahedral mesh derived from hexahedral mesh

图3 四面体网格的结点连接关系Fig.3 The nodes'relationship of tetrahedral mesh

1.3 预条件共轭梯度算法

直流电阻率法的有限元模拟需要求解大型线性方程组Ax＝b。预条件共轭梯度法是求解该问题的高效算法，其基本思想如下：

对于方程组：

作变换：

如果矩阵C满足：

那么易知：

即变换后的线性系统（5）的系数矩阵近似于单位矩阵I，求解将快速收敛。定义M＝CCT，M即称为预条件矩阵。问题转化为如何寻找到合适的预条件矩阵M。ICCG和SORCG的预条件矩阵的获取可参考文献[7，12]，在此不再赘述。

在以下的模型计算中，我们采用残差的L2范数作为预条件共轭梯度法的收敛准则，即＜10-8，其中x0为初始解，xi为第i步的解。

2 模型分析

2.1 均匀网格剖分

层状介质在地球物理勘探中是十分常见的。此处计算一个两层的地电模型，第一层电阻率为100 Ω·m，厚度为12 m，第二层为半无限空间，电阻率为10Ω·m。实际模拟计算都是在有限的区域中进行，设定计算区域在x，y，z方向上的尺度分别为（-204～204）m，（-204～204）m，（0～204）m。点电源在坐标原点激发，测量装置为单极-单极（pole-pole）。将计算区域剖分为102×102×51个单元的均匀六面体（Hex）网格（单元边长为4 m），并在此基础上进行二次剖分，将单元划分为四面体（Tet）网格。注意这两种剖分方法并不会带来单元结点数的差异，即两者结点数均为103×103×52。以下分别采用ICCG和SORCG求解，来分析它们的求解精度和收敛效率。

图4为分别采用Hex和Tet网格求解的视电阻率图。方框和十字分别代表采用Hex网格的ICCG解和SORCG解，菱形和圆圈分别代表采用Tet网格的ICCG解和SORCG解，黑色实线表示解析解。可以看出不管采用哪种网格，ICCG和SORCG都可以获得与解析解非常一致的结果，精度均符合要求。

图4 采用均匀Hex、Tet网格的ICCG和SORCG解Fig.4 Solutions from ICCG and SORCG by adopting uniform hexahedral and tetrahedral meshes

图5是收敛分析。横坐标为迭代次数，纵坐标为相对残差。可以看出，达到预设精度时SORCG的收敛次数要少于ICCG，效率相对较高，但ICCG的迭代次数也没有超过200次。需要说明的是，SORCG方法需要测试松弛因子ω，具有一定的经验性[7]，而ICCG则无需人工干预其求解过程。总的来看，两者在采用均匀网格剖分时都是较优的求解方法。

为了详细比较不同网格剖分密度时ICCG和SORCG的求解效率，我们设计了4种密度的网格：68×68×34，102×102×51，136×136×68，204×204×102，其单元边长分别为6、4、3和2 m。我们统计了不同方案的计算时间（图6），可以看出：不论是用ICCG还是SORCG求解，只要采用均匀网格，都可以获得较高的效率。即使高达400万的网格结点，在单机（DELL T7810工作站，CPU E5-2609，内存32G）上求解时间也均不超过20 min。

图5 采用均匀Hex、Tet网格时ICCG和SORCG的收敛情况Fig.5 The convergence analysis of ICCG and SORCG by employing uniform hexahedral and tetrahedral meshes

图6 采用4种剖分密度的均匀Hex、Tet网格时ICCG和SORCG的求解时间Fig.6 The ICCG and SORCG solving time when employing uniform hexahedral and tetrahedral meshes of four different mesh sizes

2.2 非均匀网格剖分

网格的不均匀剖分会严重影响有限元系数矩阵的性质，有可能引起迭代解法的失败。同样基于上述物理模型参数，此处采用不均匀的网格剖分，六面体单元数为54×54×29，在此基础上进行二次剖分为四面体，注意两者的单元结点数一致，均为55×55×30。具体剖分如下：x，y方向的剖分坐标均为（-500，-375，-275，-200，-150，-120，-90，-70，-55，-42.5，-30，-20，-15，-12，-9，-7，-5.5，-4.25，-3.25，-2.5，-2，-1.5，-1.2，-1，-0.8，-0.5，-0.2，0，0.2，0.5，0.8，1，1.2，1.5，2，2.5，3.25，4.25，5.5，7，9，12，15，20，30，42.5，55，70，90，120，150，200，275，375，500），z方向（指向地下空间为正方向）坐标为（0，0.2，0.5，0.75，1，1.25，1.5，2，2.5，3，4，5，7，9，12，15，20，25，32.5，42.5，55，70，90，120，150，200，250，325，400，500），单位：m。

计算结果如图7所示。我们发现，正如已有的研究结果[12]，采用不均匀Hex网格时ICCG的确会求解失败。究其原因，是由于ICCG在构建预条件因子时，对角矩阵D的元素出现了大量负数。对于此例，统计发现13.98%的对角元素为负，直接导致了ICCG求解失败。但是，采用本文提出的在Hex基础上继续二次剖分得到的Tet网格形成的有限元方程，其系数矩阵满足ICCG的要求，即对角矩阵D的元素全部为正数，求解成功。

比较采用Hex网格的SORCG（图7黑色圆圈）解、采用Tet网格的ICCG解（菱形）和SORCG解（十字），都与解析解（实线）吻合较好，并且符合理论预期，即小极距视电阻率趋近于第一层实际电阻率100Ω·m，大极距视电阻率趋近于第二层（半空间）的实际电阻率10Ω·m。分析不同方案的计算结果（图8）可以得出：

图7 采用不均匀网格的两层模型的视电阻率Fig.7 The apparent resistivities of a two-layer model by employing non-uniform meshes

图8 采用不均匀网格时ICCG和SORCG的收敛情况Fig.8 The convergence analysis of ICCG and SORCG by employing non-uniform meshes

（1）采用Hex不均匀网格的ICCG求解失败，但是采用本文提出的Tet不均匀网格的ICCG求解获得成功；

（2）与均匀网格结果（图5）对比发现，采用均匀网格时的迭代解法收敛率普遍较快（200次左右），而采用非均匀网格时，收敛率较慢（达500此左右），说明网格的均匀性极大影响了收敛速率；

（3）采用Tet网格可以获得和Hex网格相当的求解精度和效率，但正如前文网格分析中所述，本文提出的Tet网格的存储要求只需Hex网格的1/2，由此降低了对计算设备的要求。

3 结 论

ICCG是求解直流电阻率有限差分方程的主流方法，但在求解有限元方程有可能会失败。本文通过详细的网格分析后认为，基于六面体网格剖分的有限元系数矩阵会严重依赖于网格剖分是否均匀，即网格均匀，ICCG可以求解成功，但网格不均匀，会引起构建预条件因子时对角矩阵元素出现大量负数而求解失败。

本文提出新的网格剖分方案，即在六面体网格基础上进行二次剖分得到四面体网格。模型分析发现这种四面体网格即使剖分不均匀，也可满足ICCG构建预条件因子的要求，从而成功求解。不仅如此，这种新的四面体网格相对于六面体网格还可以减少约50%的内存空间，降低对计算设备的要求。SORCG也可高效求解直流电阻率有限元方程，但在构建预条件因子时需要额外测试选择松弛因子ω，需要一定的经验性[7]。由于三维直流电阻率模拟的区域范围较大，非均匀网格剖分具有更大的现实意义。本文提出的基于四面体网格剖分的ICCG、SORCG算法可成功求解三维直流电阻率有限元方程。

[1]RUCKER D F，LOKE M H，LEVITT M T，et al.Electrical resistivity characterization of an industrial site using long electrodes[J].Geophysics，2010，75（4）：WA95-WA104.

[2]翁爱华，祝嗣安.天然气水合物的近海底直流电测深响应[J].石油地球物理勘探，2010，45（3）：458-461.WENG A H，ZHU S A.Near sea-bottom DC sounding response for gas hydrate[J].Oil Geophysical Prospecting，2010，45（3）：458-461.

[3]强建科，阮百尧，周俊杰，等.煤矿巷道直流三极法超前探测的可行性[J].地球物理学进展，2011，26（1）：320-326.QIANG J K，RUAN B Y，ZHOU JJ，et al.The feasibility of advanced detection using DCthree-electrode method in coal-mine tunnel[J].Progress in Geophysics，2011，26（1）：320-326.

[4]LOKE M H，CHAMBERS J E，RUCKER D F，et al.Recent developments in the direct-current geoelectrical imaging method[J].Journal of Applied Geophysics，2013，95：135-156.

[5]刘洋，吴小平.巷道超前探测的并行Monte Carlo方法及电阻率各向异性影响[J].地球物理学报，2016，59（11）：4297-4309.LIU Y，WU X P.Parallel Monte Carlo method for advanced detection in tunnel incorporating anisotropic resistivity effect[J].Chinese Journal of Geophysics，2016，59（11）：4297-4309.

[6]MITCHELL M A，OLDENBURG D W.Data quality control methodologies for large，non-conventional DCresistivity datasets[J].Journal of Applied Geophysics，2016，135：163-182.

[7]王威，吴小平.电阻率任意各向异性三维有限元快速正演[J].地球物理学进展，2010，25（4）：1365-1371.WANG W，WU X P.Rapid finite element resistivity forward modeling for 3D arbitrary anisotropic structures[J].Progress in Geophysics，2010，25（4）：1365-1371.

[8]REN Z Y，TANG J T.A goal-oriented adaptive finite-element approach for multi-electrode resistivity system[J].Geophysical Journal International，2014，199（1）：136-145.

[9]吴小平，刘洋，王威.基于非结构网格的电阻率三维带地形反演[J].地球物理学报，2015，58（8）：2706-2717.WU X P，LIU Y，WANG W.3D resistivity inversion incorporating topography based on unstructured meshes[J].Chinese Journal of Geophysics，2015，58（8）：2706-2717.

[10]张钱江，戴世坤，陈龙伟，等.多源条件下直流电阻率法有限元三维数值模拟中一种近似边界条件[J].地球物理学学报，2016，59（9）：3448-3458.ZHANG Q J，DAISK，CHEN L W，et al.An approximation boundary condition for FEM-based 3-D numerical simulation with multi-source direct current resistivity method[J].Chinese Journal of Geophysics，2016，59（9）：3448-3458.

[11]李勇，林品荣，徐宝利，等.复杂地形三维直流电阻率有限元数值模拟[J].地球物理学进展，2009，24（3）：1039-1046.LI Y，LIN PR，XU B L，et al.FEM numerical modeling of 3-D DC resistivity under complicated terrain[J].Progress in Geophysics，2009，24（3）：1039-1046.

[12]WU X P.A 3-Dfinite-element algorithm for DCresistivity modelling using the shifted incomplete Cholesky conjugate gradient method[J].Geophysical Journal International，2003，154：947-956.

[13]WANG W，SPITZER K，WU X P.Three-dimensional DC anisotropic resistivity modelling using finite elements on unstructured grids[J].Geophysical Journal International，2013，193（2）：734-746.