数值模拟电磁力作用下的椭圆柱绕流

李秀文，刘 满(大连民族大学 理学院，辽宁 大连 116650)

工程应用中常常会出现一些复杂物体的绕流问题，如导弹、叶片、叶珊等的绕流问题。这些绕流问题，都会伴随着能量消耗和阻力增大，在物体表面发生边界层的分离[1]，并诱发噪声和振荡，从而使得物体造成破坏。 因此，有效的控制上述复杂物体的绕流具有重要意义，椭圆柱可以做为上述复杂物体的原型，从而研究有效的控制椭圆柱绕流是十分重要的。近些年来，人们发现许多控制椭圆柱绕流的方法, 其中利用电磁控制边界层流动是一种主动的、可实现的流体控制方法[2-4]。本文利用格子Boltzmann方法对椭圆柱绕流的电磁控制进行研究。

格子Boltzmann方法(Lattice Boltzmann Method , LBM)是上世纪80年代发展起来的一种计算流体力学的方法[5]，从分子运动论的观点出发，以微观粒子运动为基础，建立离散的速度模型，在满足质量、动量和能量守恒的条件下，得出粒子分布函数，然后对粒子分布函数进行统计计算[6]。

本文采用格子Boltzmann方法数值计算电磁力作用下的椭圆柱绕流问题，利用反弹边界条件处理曲线边界，利用动量转化法计算曲线边界的受力。计算出不同电磁力作用下椭圆柱绕流的流线，并分析了它的变化机理。

1 格子Boltzmann 方法

1.1 电磁力作用下的椭圆柱绕流

由电极条和磁条相间排列组成的激活板包覆在椭圆柱表面如图1。

(a)电极板和磁极板包覆的椭圆柱

(b)电极板和磁极板包覆椭圆柱的角度范围

将其置于弱电介质溶液中,会产生电磁力(Lorentz 力)，即作用于流体上的一种体积力，如果磁条为永久磁铁, 电极为恒定电压，则电磁力作用下的不可压缩N一S方程，其表达式为

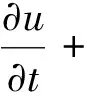
(1)

▽u=0。

(2)

式中：u是流体的速度；p为压力；Re=rau∞/γ；γ为流体运动学粘性系数；u∞为无穷远处来流速度；F是电磁力源项。

1.2 格子 Boltzmann 方程

根据文献[7]，控制方程(1)和(2)的格子Boltzmann方程可表示为

(3)

式中：eα是粒子沿第α个方向运动的速度；α=0,1,2,…8如图2；fα(xi,t)是粒子速度分布函数。平衡态分布函数

(4)

式中：c=δx/δt；δx是相邻两节点之间的距离，δt是时间步长，wα是加权系数，τ是松弛时间。电磁场作用下的电磁体积力项

(5)

宏观的密度、动量通过分布函数得到

(6)

(7)

图2 二维9速度(D2Q9)模型

将式(3)的计算分为以下两个过程。

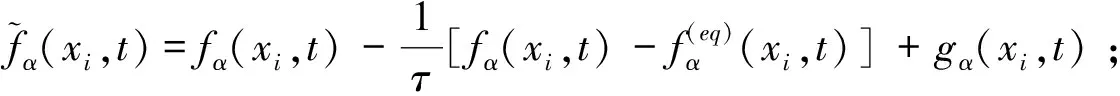
(8)

(9)

由此可以看出，碰撞是局部的，而传递与周围的节点有关。

在边界处，本文利用反弹(bounce-back)边界条件处理曲线边界，利用动量转换法计算出椭圆柱表面所受的合力[8]

(10)

2 数值模拟和计算结果

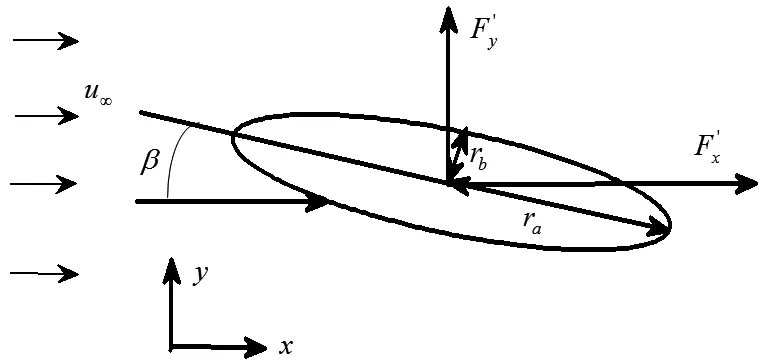
图3 流场设置

图4给出β=20°，在N=0，N=0.002情况下的流线轨迹，左侧为来流的入口，电磁力方向与流体流动方向是一致的。

(a)N=0

(b)N=0.002

图4(a)给出了在N=0，即无电磁力作用时的流线图，在椭圆柱表面流体因逆压梯度作用而出现分离，在椭圆柱尾部形成旋涡脱落，说明流动是不稳定的。

图4(b)给出了当N=0.002时，对流场施加电磁力，椭圆柱后面流线成水平发展，旋涡脱落基本消失，流动呈现稳定状态，这说明电磁力可以抑制椭圆柱后面的旋涡脱落。

3 结 论

本文用格子Boltzmann方法模拟了电磁力作用下的椭圆柱绕流，该方法计算过程简单，容易并行，适合处理该问题。在电磁力作用下，椭圆柱绕流的边界层得到改善，尾部的涡街被消除，从而使椭圆柱表面的流动分离得到很好的抑制。

参考文献：

[1] CHOI J H, LEE S J. Flow characteristics around an inclined elliptic cylinder in a turbulent boundary layer. Journal of Fluids and Structures[J], 2001, 15(8): 1123-1135.

[2] WEIER T, GERBETH G, MUTSCHKE G, et al. Control of flow separation using electromagnetic forces[J]. Flow, Turbulence and Combustion, 2003,71 (1-4):5-17.

[3] MUTSCHKE G, GERBETH G, ALBRECH T, et al. Separation control at hydrofoils using Lorentz forces[J].European Journal of Mechanics B/Fluids, 2006,25:137-152.

[4] LI X W, LU B. Numerical Investigation of Control of weakly conductive fluids by Lorentz forces， Advanced Science Letters[J].2012, 6(5), 609-613, .

[5]QIAN Y H. Lattice gas and lattice kinetic theory applied to the Navier-Stokes equation [D]. Paris: Ecole Normale Superieure and University, 1990.

[6]施卫平, 祖迎庆. 用Lattice Boltzmann 方法计算流体对曲线边界的作用力 [J]. 吉林大学学报(理学版), 2005, 43(2):132-136.

[7] GUO Z L, ZHENG C G ，SHI B C. Discrete lattice effects on the forcing term in the lattice Boltzmann method[J]. Physical Review, 2002,65, 046308.

[8] MEI R W, YU D Z, SHYY W, et al. Force evaluation in the lattice Boltzmann method involving curved geometry[J]. Physical Review E, 2002, 65(41): 041203/1-041203/14.