基于粒子群优化算法的井下目标定位方法

张 蕊，李 晖，刘赛男(沈阳工业大学 信息科学与工程学院，辽宁 沈阳 110870)

近年来无线传感器网络飞快发展，被广泛应用于管道监测、精细农业、智能交通及井下采矿等领域[1]。然而在井下环境中，传感器采集到的信息在不知道其具体位置信息的情况下是没有意义的，要快速准确地获得人员的位置信息才能为营救获得更多的时间。

无线传感器网络定位算法可划分为两类，即测距算法和非测距算法。非测距算法在成本和功耗上有一定优势，但定位精度相对较低，而且对节点密度要求较高[2]。所以在矿井环境中适合使用基于测距的定位算法，其中RSSI(Receive Signal Strength Indicator)算法不需要额外的硬件设备，能量损耗、成本低，比较适合应用在井下巷道中[3]。由于井下巷道狭长且环境复杂，测得的RSSI值误差较大，为提高定位精度，很多学者提出了改进方法。文献[4]提出了一种3DL-RD煤矿井下无线传感器网络节点三维定位算法，通过RSSI测距方式得到信标节点到未知节点的距离，将信标节点投影到与未知节点同一高度的水平面，再利用三边测量法进行平面定位，虽然能够得到较高的定位精度，但忽略了巷道顶部对定位精度的影响，会使对顶部微弧位置节点的定位出现较大误差；刘畅[5]提出井下无线传感器网络的RSSI比例差分定位算法，利用目标节点附近的信标节点到信标节点的比例差分信息，修正未知节点到信标节点的距离信息，并结合四边定位法定位，虽然提高了未知节点的坐标精度，却一定程度上增加了算法的复杂度，并使无线传感器网络系统的开销增多；文献[6]提出了一种基于矿井三维建模WSNs(Wireless Sensor Networks)多重覆盖和RSSI加权质心定位算法，该方法完全基于网络连通性，而且井下环境的传输模型与质心算法理想的球型模型有很大差别；李宁等[7]提出基于改进遗传算法的矿井人员定位新算法，即以无线传输信号理论模型为基础，周期性获取信号传输路径衰减指数的加权平均值，并结合遗传算法进行优化，该方法是研究的热点问题智能群体算法[8-9]，在井下环境下遗传算法大量的计算导致在进化后期搜索效率较低，稳定性差。

本研究针对井下的复杂环境提出一种基于粒子群优化算法的井下目标定位方法。结合井下巷道[10-11]的特点规则放置信标节点，将未知节点和信标节点间的估计距离和测量距离的均方误差作为粒子群算法优化的目标函数，并引入惯性权重[12-13]，再通过算法的迭代运算找到适应性强的粒子，提高算法精度。该方法收敛速度快，计算量小，可靠稳定，在提高测距精度的同时也增加了对井下巷道复杂环境的适应性。

1 相关原理

1.1 三维信标节点布置

煤矿井下巷道是狭长的，顶部呈微弧型，可以近似地看做长方体。分别在各对角上布置一对信标节点，并在每个小区块的微弧顶部中间布置一个信标节点，这样每个小区块仅布置5个信标节点。这样的布置方法可以将定位区域区块化，避免区块内节点布置过密，减小节点间通信干扰，使节点测距更准确。信标节点布置规则如图1。

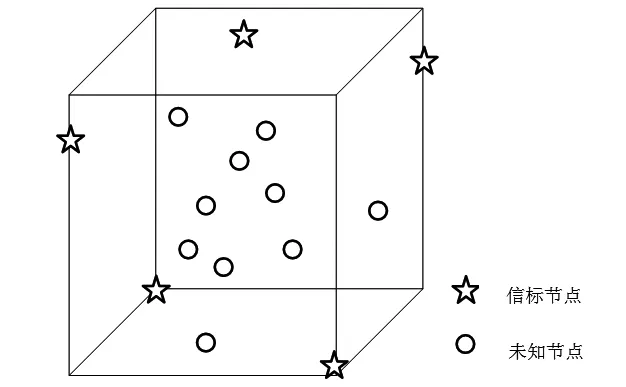
图1 信标节点布置规则

1.2 RSSI测距模型

本文采用在复杂环境中广泛应用的对数-常态分布模型和井下巷道RSSI测距分析[14]得出的参数，对井下无线信号传播进行建模和估计。对数-常态分布模型的表达式为

(1)

式中：PL(d) 为经过距离d后的路径损耗；PL(d0) 为经过单位距离后的路径损耗；d0表示单位距离，一般设为1 m；n表示为路径损耗因子，它取决于无线信号传播的环境；Xσ表示均值为0、标准差为σ的高斯噪声，其值受周围环境和障碍物影响，一般为4～10。接收端的信号强度为

PR(d)=PT-PL(d) 。

(2)

式中：PR(d)即为接收信号强度指示RSSI；PT为信号的发射功率，文献[14]给出的参数为0 dBm。

综上有式(1)和式(2)可以得出RSSI值与距离的关系为

RSSI=-10nlgd+A。

(3)

式中：d为参考节点到未知节点的距离；A为常数。文献[10]将实验所得的数据通过处理再进行线性拟合,得出拟合直线方程

y=-24.494x-37.200 4 。

(4)

式中：y表示RSSI值；x表示距离d的对数；路径损耗因子n为2.449 4。因此信标节点和未知节点间距离与RSSI的关系可以表示为

(5)

2 粒子群优化算法

2.1 粒子群算法原理

粒子群优化算法(Partical Swarm Optimization,PSO)是模拟鸟群觅食过程中的集体协作行为而提出的一种基于群体智能的全局随机搜索算法[15]。在PSO算法中，每个优化问题的解都是搜索空间中的一只“鸟”，称之为粒子。首先初始化一群随机粒子，然后粒子们就追随当前的最优粒子在解空间中搜索，即通过迭代找到最优解[16]。假设d维搜索空间中的第i个粒子的位置和速度分别为Xi=(xi,1xi,2…xi,d)和Vi= (vi,1vi,2…vi,d)，在每一次迭代中,粒子通过跟踪两个最优解来更新自己，第一个就是粒子本身所找到的最优解，即个体极值pbest，Pi= (pi,1pi,2…pi,d)；另一个是整个种群目前找到的最优解，即全局最优解gbest,Pg。在找到这两个最优值时，粒子根据式(6)、(7)来更新自己的速度和新的位置。

vi,j(t+1)=wvi,j(t)+c1r1[pi,j-xi,j(t)]+c2r2[pg,j-xi,j(t)] ；

(6)

xi,j(t+1)=xi,j(t)+vi,j(t+1),j=1,2,…,d。

(7)

式中：w为惯性权重；c1和c2为正的学习因子，常设c1=c2=2；r1和r2是介于0到1之间均匀分布的随机数；t为当前迭代次数。

粒子群算法的性能很大程度上受算法的控制参数影响，w的合适选择可以使粒子具有均衡的全局搜索能力和局部搜索能力，w较小有利于提高算法的局部搜索能力，w较大可以提高算法的全局搜索能力。因此采用线性递减的惯性权重方法[8-9]，即线性递减权重粒子群算法(Linear Degression Weight,LinWPSO)，权值公式为

(8)

式中：T是终止迭代次数；wmax和wmin为惯性权重w的最大值和最小值。

2.2 目标函数的设定

目标函数是衡量粒子优劣的标准，在算法每一次迭代的过程中，需要根据目标函数值来更新粒子的位置。假设定位区域内部署了m个信标节点，其坐标为(xi，yi，zi)，i=1,2…，m，未知节点坐标为(x，y，z)，通过RSSI方法测量得到的距离为di。为了降低测距误差，将未知节点和信标节点的测量距离和估算距离的均方误差作为优化的目标函数，目标函数为

f(x,y,z)=

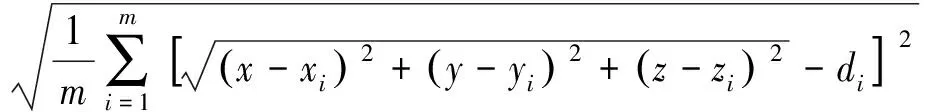
(9)

2.3 方法流程

(1)在目标区域部署5个传感器信标节点，通过RSSI方法得到未知节点与信标节点的距离di。

(2)初始化种群。初始粒子i的位置Xi=(xi,1xi,2…xi,d)，速度为Vi= (vi,1vi,2…vi,d)。

(3)评价每个粒子的适应度(即目标函数值)，将当前粒子的位置和适应值存储在各粒子的pbest中，将所有pbest中适应值最优个体的位置和适应值存储于gbest中。

(4)用式(7)和式(8)来更新粒子的速度和位置。

(5)对于每个粒子，将其适应值与其经历过的最好位置作比较，如果较好，则将其作为当前的最好位置。

(6)比较当前所有pbest和gbest的值，更新gbest。

(7)若满足迭代终止条件，输出全局历史最优解，否则返回步骤(4)继续寻优。

3 仿真结果及分析

为了验证和分析本文方法的定位精度、抗噪等性能，进行了Matlab仿真实验，并与四边测量法、加权最小二乘法以及文献[6]提出的RSSI加权质心算法进行了对比。由于在井下特殊环境下，RSSI测距精度受其影响，将仿真环境设为长5 m、宽5 m、高6 m的长方体三维区域。RSSI测距模型中的高斯噪声标准差为8，信标节点密度为33%。定位误差为单次实验得出的估计节点与未知节点间距离的差值。平均定位误差则为实验重复30次得出的定位误差的均值。

3.1 平均定位误差

本文方法定位效果图如图2。节点总数为15，其中信标节点5个，按照本文节点部署规则布置；未知节点10个，随机分布在三维区域内。未知节点与估计节点间的连线表示定位误差。定位的仿真数据见表1，平均定位误差为0.877 m。

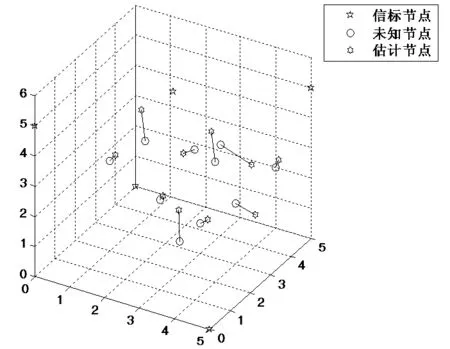
图2 定位效果图

表1 定位仿真数据

3.2 性能对比分析

在本文设定的仿真环境中将本文方法与四边测量法、加权最小二乘法和RSSI加权质心法的性能进行对比，实验重复30次得出的平均定位误差的数据特征见表2，单次实验误差仿真图如图3。

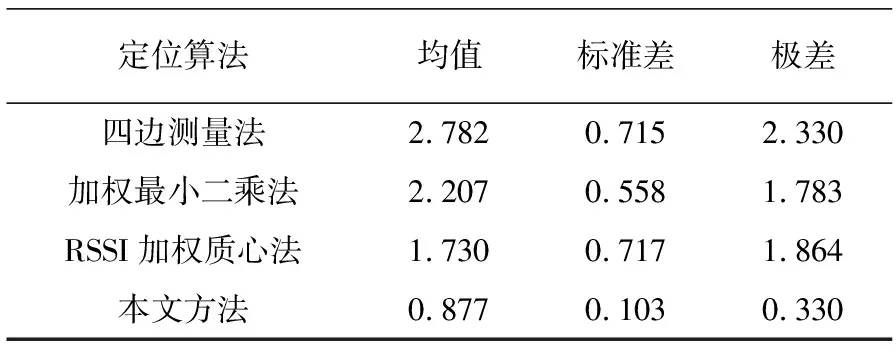
表2 平均定位误差对比

(a) 四边测量法 (b) 加权最小二乘法

(c) RSSI加权质心法 (d) 本文方法

分析表2中的数据可知本文方法标准差最小，即围绕均值波动的幅度最小，算法最稳定，四边测量法标准差与均值相比波动最大，定位性能最不稳定；本文算法极差最小，也就是误差变化幅度最稳定，而四边测量法和RSSI加权质心法极差较大，因为RSSI加权质心算法受网络连通度影响较大，误差波动最不稳定。图3定位误差值中可以看出，四边测量法的定位误差最大，四边测量法和加权最小二乘法都是通过测距来估计未知节点的，所以易造成误差积累。RSSI加权质心算法定位误差比四边测量法和加权最小二乘法稍小，但是当部分信标节点失效时，该算法稳定性会急剧下降。而本文算法是在四边测量法的基础上对测距误差进行优化，由上图可知定位误差明显小于其他三种方法，平均定位误差可降至0.877 m，对于定位精度和稳定性综合考虑，本文算法更优。

由于在巷道中无线传输信号受到恶劣环境影响，为分析算法性能，仿真得出四种定位算法在不同噪声强度下的平均定位误差如图4。高斯白噪声标准差取值从5递增到20，所有平均定位误差都随着噪声强度的升高而增加，当噪声强度超过13之后误差增加的幅度均有明显提升。四边测量法的平均定位误差从2.15 m增加到9.45 m，增长幅度最高，因为四边测量法受测距影响较大。本文算法平均定位误差由1.21 m增长到4.65 m，增长幅度最小，因此抗噪性最好。

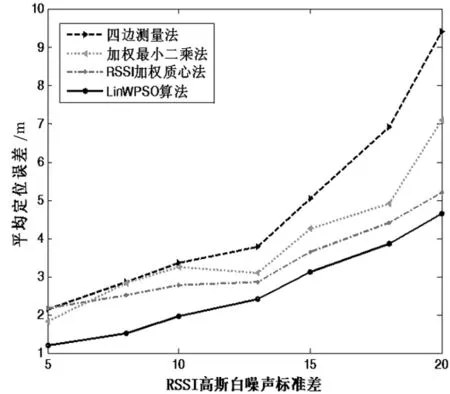
图4 噪声强度对定位误差的影响

定位误差与信标节点密度关系如图5。信标节点密度由10%增加到40%，RSSI加权质心法的平均定位误差由4.75 m下降到0.95 m，误差下降幅度较大，这是由于质心算法对网络连通度要求较高。四边测量法只用四个信标节点定位，随着信标节点密度的增加定位精度无明显提高。本文算法平均定位误差从2.82 m下降到0.76 m，定位精度明显好于其他三种算法，稳定性好于RSSI加权质心算法，当部分节点失效时，网络连通性下降，仍然可以保持良好的定位精度。

图5 定位误差与信标节点密度的关系

4 结 语

本文根据井下巷道的复杂环境提出一种基于粒子群优化的井下目标定位方法。结合井下巷道的特点规则放置信标节点，减小节点间通信干扰，合理分配资源。在井下RSSI测距模型的基础上引入线性递减权重粒子群优化算法对测距误差进行优化。将未知节点和信标节点间的估计距离和测量距离的均方误差作为粒子群算法优化的目标函数，再通过算法的迭代运算找到适应性强的粒子。仿真实验显示该算法较对比算法定位精度更高，抗噪性更好，可靠稳定，在井下巷道环境中适应性更强。

参考文献：

[1] HU Q S，ZHANG S，WU L X，et al. Localization techniques of mobile objects in coal mine：challenges，solutions and trends[J] .Journal of China Coal Society,2016,41(5):1059-1068.

[2] 王刚刚，王正.无线传感器网络定位算法原理与研究进展概述[J] .木工机床，2016(2)：18-20.

[3] 任子晖，顾靓雨，周萌萌.基于无线传感器网络的改进RSSI井下定位算法的矿井人员定位系统设计[J].煤矿开采，2015，20(3)：136-139.

[4] 朱晓娟，王军号，孟祥瑞.煤矿井下无线传感器网络节点三维定位算法[J].计算机应用，2012，32(4)：927-931.

[5] 刘畅.井下无线传感器网络的RSSI比例差分定位算法[J].电脑知识与技术，2017，13(6)：44-46.

[6] 方旺盛，雷高祥，李宁.基于矿井三维WSNs多重覆盖和RSSI的加权质心算法[J].传感器与微系统，2016，35(5)：128-131.

[7] 李宁，王李管，贾明涛，等.基于改进遗传算法的矿井人员定位新算法[J].中南大学学报，2016,47(3)：930-935.

[8] DU W B ，GAO Y ，LIU C，et al.Adequate is better：partical swarm optimization with limited-information[J].Applied Mathematics & Computation,2015,268：832-838.

[9] TAHERKHANI M ，SAFABAKHSH R .A novel stability-based adaptive intertia weight for partical swarm optimization[J].Applied Soft Computing,2016,38：281-295.

[10] 孙波，刘冬阳，徐奉，等.基于RSSI的煤矿井下巷道定位技术误差分析[J].煤炭学报，2014，39(S2)：609-614.

[11] ZHANG B H，FAN J，DAI G J,et al.A hybrid localization approach in 3D wireless sensor network[J].International Journal of Distributed Sensor Networks，2015:20.

[12] SHI Y，EBERHART R C.A modified particle swarm optimizer[J].Proceedings of IEEE International Conference on Evolutionary Computation，Anchorage,1998:69-73.

[13] 杨英杰.粒子群算法及其应用研究[M].北京：北京理工大学出版社，2017：14-20.

[14] 郭雁一夫，刘宏立，徐琨，等.基于WSN的井下巷道RSSI性能分析[J].计算机工程与应用，2016,52(17)：128-132.

[15] ZHANG Y D，WANG S H，JI G L. A comprehensive survey on partical swarm optimization algorithm and its applications[J]. Mathematical Problems in Engineering,2015(1)：1-38.

[16] TRELEA I .The partical swarm optimization algorithm：convergence analysis and parameter selection[J].Information Processing Letters，2016，85(6)：317-325.