仿生四足机器人自适应粒子群优化控制

李 冰，苏文海，息晓琳，靳亚东

(东北农业大学 工程学院，哈尔滨 150030)

0 引言

随着我国农业机械自动化水平的不断提高，仿生足式机器人以其特有的优势在农业作业领域有着广泛的应用[1-3]。其中，仿生四足机器人作为农业机器人之一，具有牛、马等四足哺乳动物的运动特点，对复杂环境的适应性及运动的灵活性等方面与其他移动方式相比，具有非常大的优势。在足式机器人研究领域中，综合其机构复杂度和稳定性，仿生四足机器人是一种较优的选择方式，并且得到了广泛应用[4-5]。

目前，液压系统在机械自动化领域的应用多采用基于PID的控制策略[6-7]，但常规的PID控制器不能很好地控制像机器人这种含有非线性和时变参数的系统[8]。针对有效提高对仿生四足机器人液压伺服系统的控制精度，减小由位置内环PID控制液压伺服系统过程中产生的高频振动对仿生四足机器人稳态行走的影响，本文引入自适应粒子群(PSO)控制算法[9-13]。把PID控制与自适应粒子群(PSO)算法的优点相结合，通过自适应粒子群控制算法对PID参数进行实时调整，能很好地改善液压伺服系统本身存在的非线性因素及时变参数对液压传动稳态控制的影响，使仿生四足机器人能够平稳行走。

1 液压系统传递函数的建立

1.1 仿生四足机器人的结构

仿生四足机器人主要由机身和4条相同结构的腿组成，4条腿的安装方式采用前肘后膝式[14-15]，如图1所示。

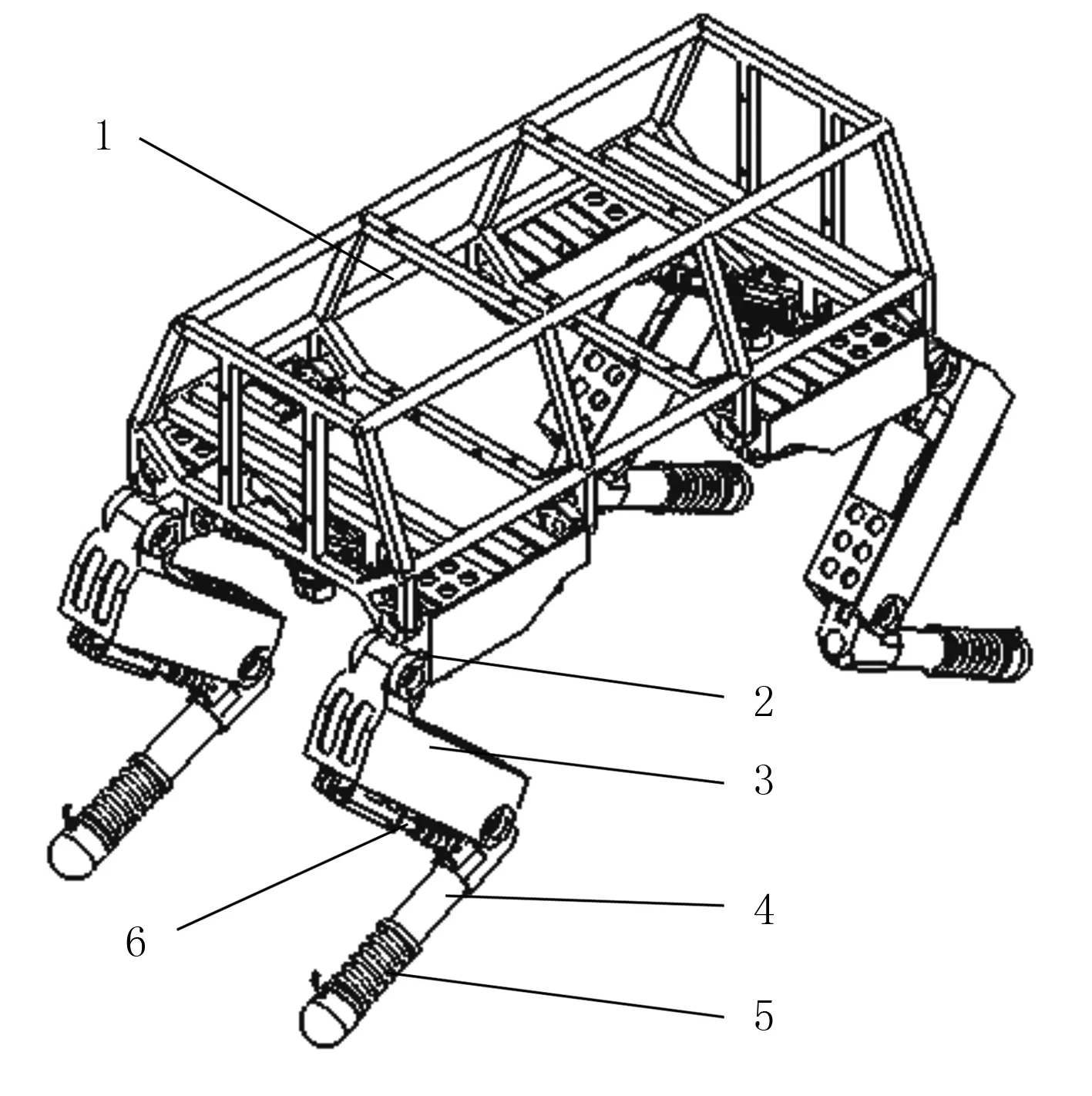
1.机身 2.机节 3.大腿 4.小腿 5.弹性元件 6.液压伺服系统图1 仿生四足机器人结构图Fig.1 Structure of bionic quadruped robot

构成每条腿的结构包括机节、大腿和小腿，因此每条腿由3个液压缸驱动，所以仿生四足机器人共有12个液压伺服系统。同时，在机器人足底部位安装弹性元件，使仿生四足机器人在行走过程中，减轻了在落地时足端对腿部关节产生强烈的刚性冲击[16]。其中，机节控制侧摆，大腿和小腿控制前进距离及抬腿高度。

1.2 液压伺服阀数学模型

液压伺服阀包括力矩放大器和伺服阀两部分。力矩放大器是将PID控制器输出的偏差电压e转化为驱动电流I，在一定频率范围内，力矩放大器可以近似看成比例环节Ka，则

(1)

伺服阀是具有非线性特性的功率放大器，其传递函数用振荡环节来近似表示，即

(2)

其中，Kv为伺服阀流量增益；ωv为伺服阀的固有频率；ξv为伺服阀的阻尼比。

1.3 缸体传动数学模型

缸体传动一般可以近似等效为积分加上二阶振荡环节，其传递函数为

(3)

其中，ωn为液压缸固有频率；ξ为动力元件阻尼比。

考虑到外界负载力对液压系统干扰影响时，其扰动传递函数为

(4)

其中，Kce为阀控缸的总流量压力系数；Ap为油缸活塞的有效面积；Vt为油缸的有效面积；βe为油缸活塞的有效面积。

1.4 液压伺服位置系统方框图

由1.2～1.3节所得的表达式可推导出仿生四足机器人液压伺服系统的模型结构图，如图2所示。

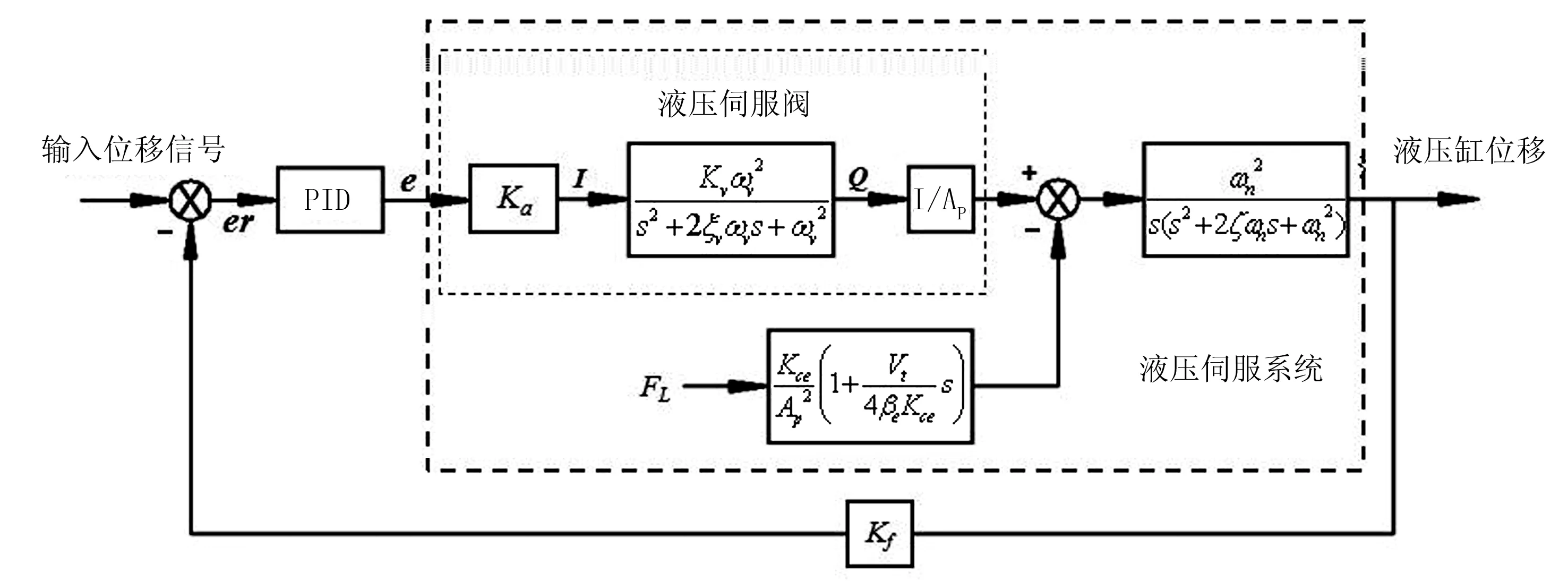
图2 液压伺服系统方框图Fig.2 Hydraulic servo position system block diagram

2 PSO- PID控制器原理

PSO-PID控制器原理是在常规PID控制器的基础上，用误差及误差的变化率作为输入，利用自适应粒子群(PSO)算法对PID的3个参数Kp、Ki、Kd进行迭代搜寻，实现对整个粒子群空间的寻优操作，找到最优解，减少信号跟踪误差，提高控制系统的快速响应速度和稳定性能。

2.1 粒子群优化原理

在PSO算法中，由m个粒子组成的群体在维度为D的空间中搜寻，第i个粒子用一个D维的向量Xi=(xi1,xi2,…,xiD)来表示。每一个粒子的位置xis代表一个可能解，代入适应度函数[式(5)]算出它的适应值，根据适应值的大小来判断解的好坏，确定最优极值。

(5)

其中，e(t)为误差信号。

在每次迭代过程中，粒子通过跟踪个体极值Pis与全局极值Pgs的方式如(见图3)来更新自己。

图3 粒子位置更新方式Fig.3 Particle position update

由图3可知，在每次迭代计算中，粒子将按照式(6)来更新搜寻的速度和位置，即

(6)

其中，i=1,2,…,m；s=1,2,…,D；非负常数C1和C2为加速度因子，其中C1用来调节粒子飞向个体最好位置方向的距离，C2用来调节粒子飞向全局最好位置方向的距离，其值一般取2[17]；r1和r2为相互独立的随机数，变化范围在0～1之间；w为惯性权值；n为迭代次数。为了防止粒子在迭代更新过程中存在离开搜寻空间的可能，Vis通常限定在一个范围内。

2.2 自适应权值PSO算法

式(6)中，惯性权值w是PSO算法的一个重要参数，用来调整上一次搜寻速度对当前搜寻速度的影响，其大小影响单个粒子通过局部搜寻和全局搜寻速度。

根据文献[18]所提出的自适应权值的PSO算法，按照式(7)更新权值。让单个粒子经过每一次迭代更新，判断全局最优位置的距离选取合适的w值，使单个粒子的搜寻速度在全局与局部之间达到最佳平衡状态，让粒子群在迭代前期能够达到较好的全局搜寻能力，在迭代后期能够使粒子群具有良好的局部搜寻能力和收敛速度。

(7)

其中，w(t)为粒子群在第t代时的惯性权重值；wmax、wmin为权重值区间的上界和下界；f为粒子实时的目标函数；favg为当前所有粒子的平均值；fmin为当前所有粒子的最小值。

2.3 PID控制器的参数优化

为了能够获得最佳的PID控制参数，将PID 3个参数设为粒子群的粒子，粒子空间维数定为三维并标定种群规模。然后，对每个粒子(随机解)的搜寻速度和位置进行初始化，在搜索过程中每个粒子的搜寻速度会按照粒子的寻找经验和群体的寻找经验进行实时调整，并逐步靠近目标值，最后找到最优解，得到PID控制器的最优参数。基于自适应粒子群算法的PID控制仿生四足机器人结构流程如图4所示。

图4 粒子群算法的PID控制系统结构Fig.4 The structure of PID control system based on particle swarm optimization

PID控制器直接对液压伺服系统进行位置闭环控制，而自适应PSO算法根据式(5)把位移传感器反馈来的误差信号及PID控制器的输出信号进行评价运算，对PID控制器的3个参数进行实时优化。

3 仿真试验分析

为了验证自适应粒子群(PSO)算法优化PID控制策略在仿生四足机器人液压伺服系统稳态中的有效性，对控制策略的跟踪特性和对液压传动时产生振动的抑制作用进行研究。为此，仿真试验部分首先测试适应函数曲线的变化情况以验证控制算法的快速收敛性，然后进行正弦响应测试验证。通过MatLab/Simulink仿真试验来分析所设计的液压伺服控制系统的设计效果。仿真试验所用到的液压缸和液压伺服阀的数据如表1和表2所示。

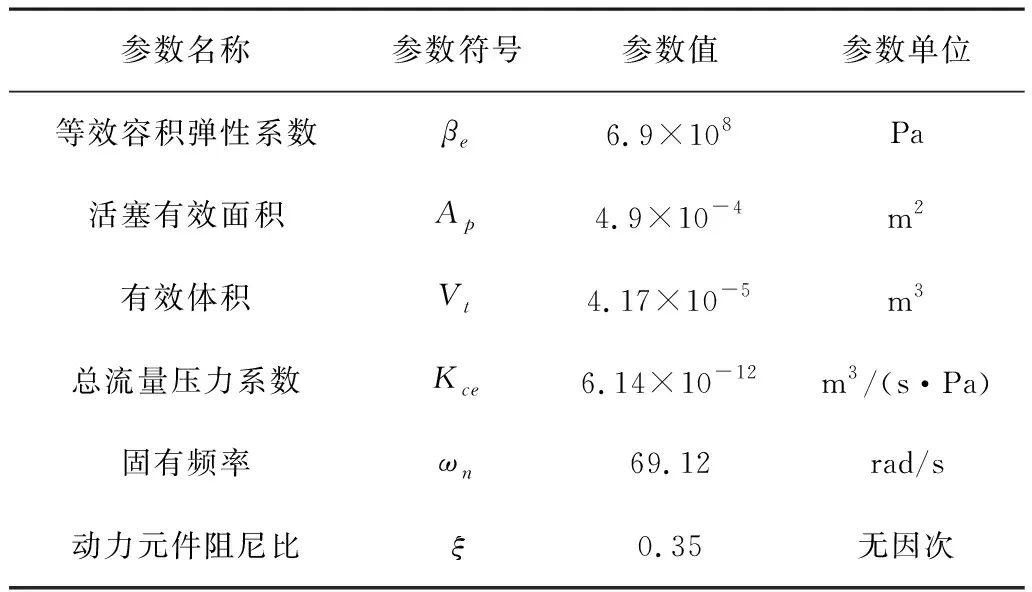
表1 液压缸的技术参数

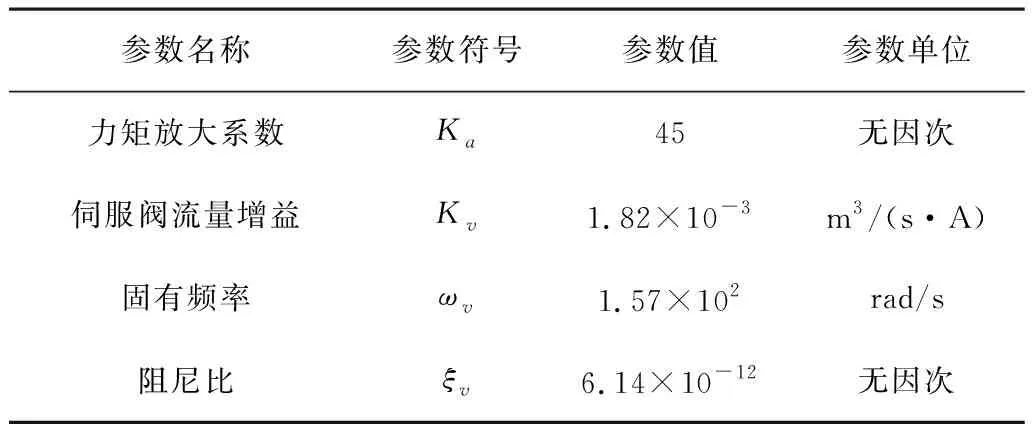
表2 液压伺服阀参数

3.1 适应度曲线测试

根据1.4节所构建的液压伺服控制系统仿真模型、增量式控制PID与式(5)一起作为仿真目标函数，利用MatLab软件编写程序并进行仿真测试。自适应PSO-PID控制器参数选择如下：

①惯性因子，Wmax=1.2，Wmin=0.2；②加速因子，C1=2，C2=2；③粒子群维数，Dim=3；④种群规模，SwarmSize=50；⑤最大迭代次数，Iter=50；⑥最小适应值，Fit=0.1。

如图5所示，经过30次的仿真测试，迭代次数均在10～15次左右(图5为12次)，其适应值达到最小值之后就趋于稳定状态，并且PID参数随着迭代次数的增加逐步接近目标值。由此说明自适应粒子群(PSO)算法对于优化PID控制器参数具有搜索能力强、收敛速度快和计算精度准确的特点，保证了对仿生四足机器人液压伺服系统控制的稳定性。

图5 适应度曲线Fig. 5 Fitness curve of hydraulic servo position model

3.2 正弦位移信号响应测试

试验中，对液压伺服控制系统仿真模型施加位移为S(t)=30sin(6.3t+π/10)mm的正弦测试信号，仿真时间为4s，采样时间为1ms，仿真结果如图6所示。

图6(a)为常规PID控制器控制液压伺服系统模型。从图6中可以看出：当系统扰动项施加了干扰载荷为FL=50sin(20t)N时，信号跟踪性能较好，但跟踪信号在峰值处出现了明显的高频振动。与图6(a)相比，图6(b)经过自适应粒子群(PSO)优化之后，跟踪信号与输入信号几乎重合且在系统扰动项施加相同的干扰载荷之后，液压伺服系统模型的振动情况得到了明显改善，动态性能有明显提高。

仿真结果表明：基于自适应粒子群算法优化PID控制液压伺服系统的方法，能够满足仿生四足机器人液压系统的传动性能。

(a) 常规PID控制

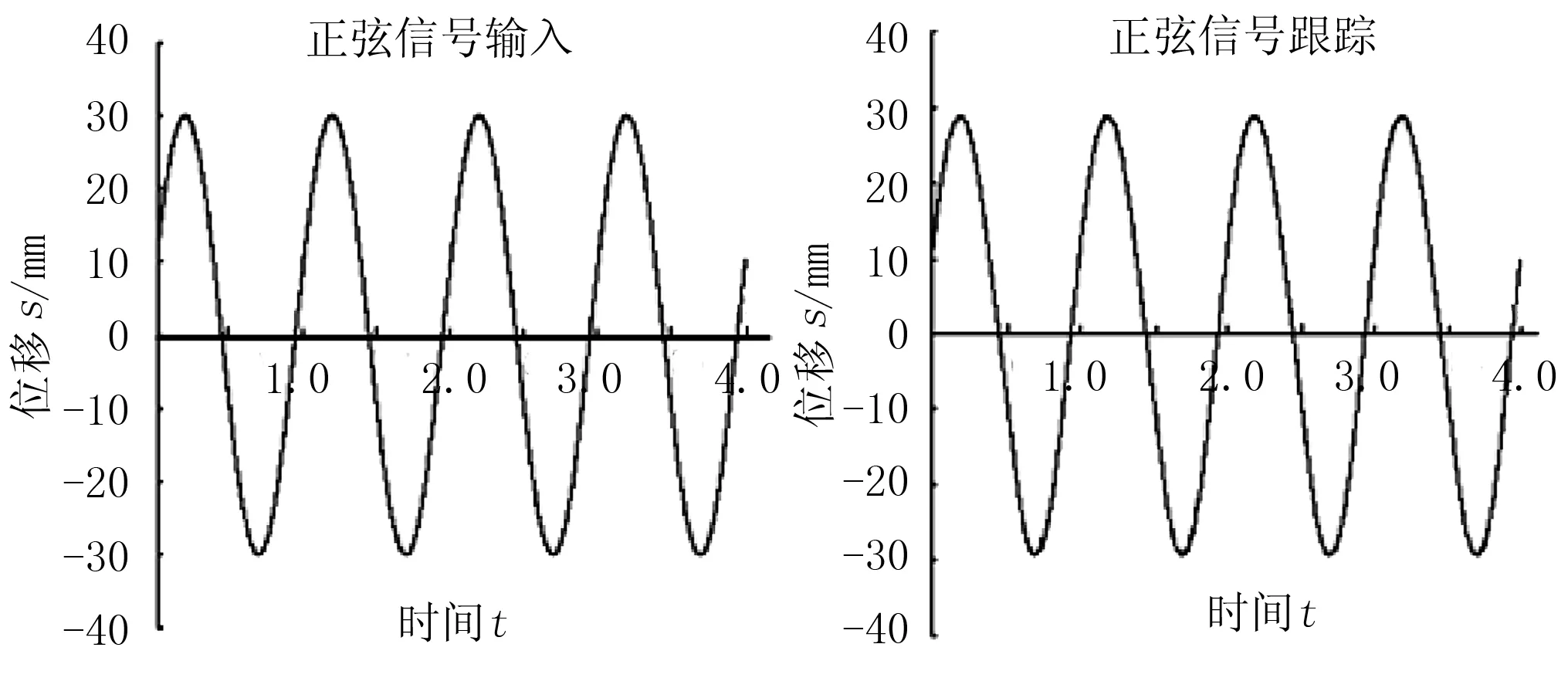
(b) 粒子群优化算法优化PID控制图6 正弦信号仿真结果Fig.6 Simulation results of sine signal

4 试验研究

为验证仿真试验的有效性，基于对四足机器人的步态及PSO-PID控制算法编写程序，在所设计的仿生四足机器人试验样机(见图7)上进行试验测试。

图7 仿生四足机器人试验样机Fig.7 Experimental prototype of bionic quadruped robot

4.1 液压伺服控制器硬件设计

试验中，采用研华PC104作为主控计算机(见图8)处理数据，连接外置网卡，在MatLab命令窗口中输入xpcexplr，在其弹出的窗口中根据网卡型号制作XPC的引导文件作为PC104主控计算机的实时系统；同时，将编写好的程序通过MatLab/simulink外部模式编译到PC104存储区。

腿控制器采用研华PC104为核心控制器，用于与主控计算机实现CAN 总线通讯和执行液压缸位移/力伺服控制算法。HIT-PC104-HXL-515用于采集每个关节的力/位传感器信息，并进行AD转换。HIT-PC104-HXL-P520用于DA转换产生液压阀控制信号。

(a) 主控计算机 (b) 腿控制器图8 液压伺服控制器硬件Fig.8 Hydraulic servo controller hardware

4.2 仿真结果与试验结果的对比

试验中，足端轨迹信号取前进距离S=200mm；抬腿高度H=50mm；运动周期T=2s；落地初速度V0=30mm/s；采样时间ts=1ms。仿生四足机器人试验样机在自身负载的作用下，以对角步态运行30s，分别进行常规PID控制和自适应粒子群(PSO)优化PID控制方法进行试验研究，试验结果如图9所示。

图9(a)为大、小腿的位移输入信号，通过观察两种控制方法的信号跟踪情况，比较其对液压伺服系统的控制能力。图9(b)为常规PID控制的液压伺服系统，与仿真试验比较，反馈位移基本上能够跟踪上输入位移信号，但大腿的液压伺服系统有振动，小腿的液压伺服系统在足端接触地面时更为明显，试验样机在行走时抖动较大。图9(c)可知，基于自适应粒子群(PSO)优化PID控制的液压伺服系统能够达到预期的试验效果，液压缸在传动时由于摆动相及支撑相的交替造成负载时变所产生的振动基本消除了，行走过程平稳，试验样机的动态稳定性能得到了明显改善，同时也验证了仿真试验结果。

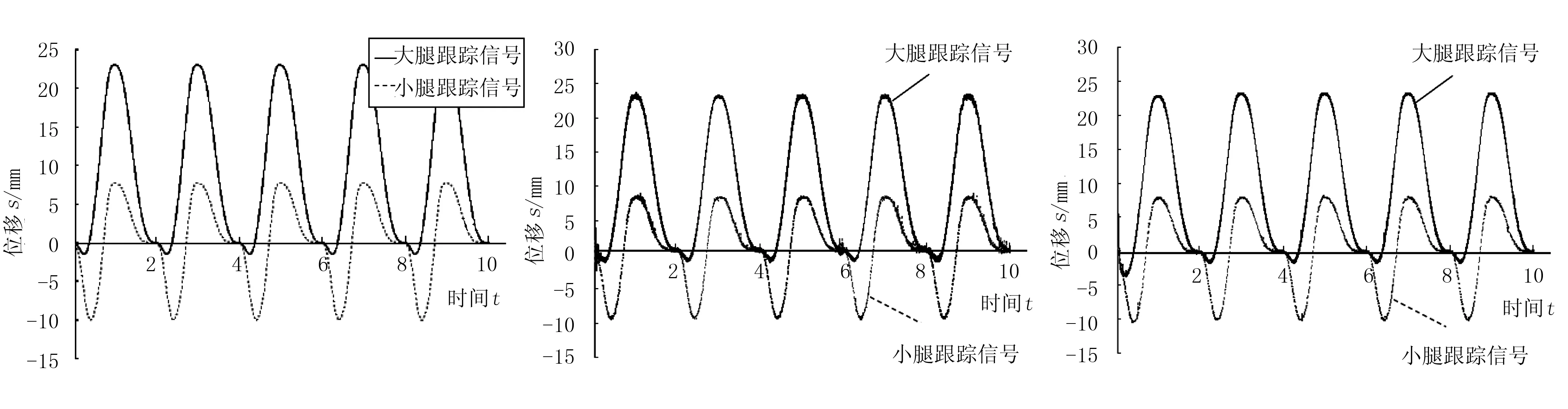
(a) 位移输入信号 (b)常规PID位置闭环控制 (c) 自适应粒子群优化PID位置闭环控制图9 两种控制性能试验测试结果Fig.9 Test results of two kinds of control performance

5 结论

1) 仿生四足机器人采用自适应粒子群(PSO)优化PID控制液压伺服系统，该方法具有很强的自适应性和快速收敛性等优点，能够对参数粒子快速通过全局搜索，根据实际情况找到最优控制参数,满足实时控制PID参数优化需求。

2) 试验结果表明：基于自适应粒子群(PSO)优化PID的控制方法对仿生四足机器人液压伺服传动系统有很好的控制能力，能够对系统进行准确的辨识，有效地对给定位移信号进行跟踪，抑制液压伺服驱动非线性和参数时变性等问题所引起的高频振动，提高了仿生四足机器人液压伺服系统的液压传动性能，保证仿生四足机器人行走平稳。

3) 为仿生四足机器人在基于力的外闭环控制，增强腿部关节的主动柔顺性，提供了稳态条件。

参考文献：

[1] 张金柱，金振林，陈广广.六足步行机器人腿部机构运动学分析[J].农业工程学报，2016,32(9)：45-52.

[2] 纪超，冯青春，袁挺，等.温室黄瓜采摘机器人系统研制及性能分析田[J].机器人，2011，33(6)：726-730.

[3] 牛雪梅，高国琴，刘辛军，等.三自由度驱动冗余并联机构动力学建模与试验[J].农业工程学报，2013，29(16)：31-41.

[4] 张皓然.四足除草机器人的静态步行及稳定性研究[D]. 昆明：昆明理工大学，2015．

[5] 张皓然,戈振扬,于英杰，等.除草用四足机器人稳定性的判定与分析[J].湖南农业大学学报，2015,41(3)：340-344.

[6] 鲁植雄，龚佳慧，鲁杨，等.拖拉机线控液压转向系统的双通道PID控制仿真与试验[J].农业工程学报，2016,32(6):101-106.

[7] 陈洁,原思聪,刘道华.PID控制在高速数控压机液压系统中的应用[J].机械设计与制造，2010(6):67-69.

[8] 许行之.自整定模糊PID控制策略在机器人控制系统中的应用[J].制造业自动化，2009,31(8):105-107.

[9] 熊伟丽，徐保国，周其明．基于改进粒子群算法的PID参数优化方法研究[J]．计算机仿真，2005，31(24) :41-43．

[10] 于颖，李永生，於孝春．粒子群算法在工程优化设计中的应用[J]．机械工程学报，2008，44(12):226-231．

[11] 罗春松，张英杰，王锦锟．改进粒子群算法整定PID数研究[J]．计算机工程与应用，2009，45(17):225-227．

[12] 杨智，陈颖．改进粒子群算法及其在PID整定中的应用[J]．控制工程，2016，23(2)：261-266．

[13] 刘志雄，梁华．粒子群算法中随机数参数的设置与实验分析[J]．控制理论与应用，2010，27(11):1489-1496．

[14] Xiuli Z,Haojun Z,Xu G,et al.A biological inspired quadruped robot:structure and control[C]//IEEE International Conference on Robotics and Biomimetics(ROBIO),HongKong:IEEE Proceedings,2005:387-392.

[15] Meek S,Kim J,Anderson M.Stability of a trotting quadruped robot with passive,underactuated legs[C]//ICRA 2008. IEEE International Conference on Robotics and Automation,2008.Pasadena:IEEE Proceedings,2008:347-351.

[16] 李满天，蒋振宇，郭伟，等. 四足仿生机器人单腿系统[J].机器人,2014,36(1):21-28.

[17] Kennedy J. Thinking is social: experiments with the adaptive culture model [J]. Journal of Conflict Resolution, 1998, 42(1): 56-76.

[18] 史娇娇，姜淑娟，韩寒．自适应粒子群优化算法及其在测试数据生成中的应用研究[J]．电子学报，2003,41(8) :1555-1559.